基于刚度矩阵法的并联机构静刚度特性分析*
2022-08-30朱春霞孙家宁
朱春霞 孙家宁 赵 元
(①沈阳建筑大学机械工程学院,辽宁 沈阳 110168;②沈阳工学院机械工程与自动化学院,辽宁 抚顺 113122)
因并联机构具有大承载、小惯性和运动平稳等特点[1-2],一直应用于工业生产中并且在新的领域中不断开拓[3-4]。而并联机构上述特点中对其本身应用更为关键的因素是刚度,刚度是机构负载后运动精度与稳定性的重要因素[5]。由于并联机构的刚度随输出位置的改变而变化,使得机器人设计中涉及的刚度须建立机构输出位置与刚度的联系。因此,刚度特性分析是为设计高刚度的并联机器人而进行参数优化的重要步骤。
目前对于并联机构的刚度研究许多学者从不同的方面进行切入。熊万涛等[6]对闭式C形并联机床机身进行静刚度分析,求得力雅可比矩阵,最后利用有限元对静刚度进行分析,得到动平台越靠近静坐标系原点,机架的静力学性能越好的结论;梅瑛等[7]对(3-RPR+R)&UPS并联机构分析,得出约束力下机构螺旋、整体的刚度矩阵,以此得出该机构的刚度模型。陈超等[8]利用3-RPS并联机构,从单元柔度矩阵角度出发,结合小变形叠加等原理建立机构的静刚度模型。樊大宝[9]依托3-UPRP并联机床进行分析,依据等效刚度法求出刚度矩阵,而对整机刚度矩阵的求解采用等效刚度的原理。Wan X J等[10]针对冗余并联机构,基于动能法、虚功原理和微扰法,求出质量矩阵和刚度矩阵,并以此来衡量冗余并联机构的解耦程度。
通过上述分析,发现目前对并联机构静力学的分析主要是理论与软件仿真方面,缺乏对机械结构设计方面的理论指导。这就启发本文通过3-TPT并联机构,对其进行静力学进行分析,以机构在受力平衡时,机构动力与负载的联系为切入。之后,使用并联机构刚度矩阵法来求解机构刚度矩阵。并对支链轴向刚度进行了求解。最后以并联机构运动轨迹上的3个点来最终求解,从而得出机构整体刚度,以给予并联机构设计的理论支撑。
1 静力学分析与刚度矩阵求解
3-TPT并联机构的构成为动平台和静平台。动平台包括3条支链,而支链又包含驱动及虎克铰。此处只考虑标准条件下的3平移自由度3-TPT并联机构[11],如图1所示。
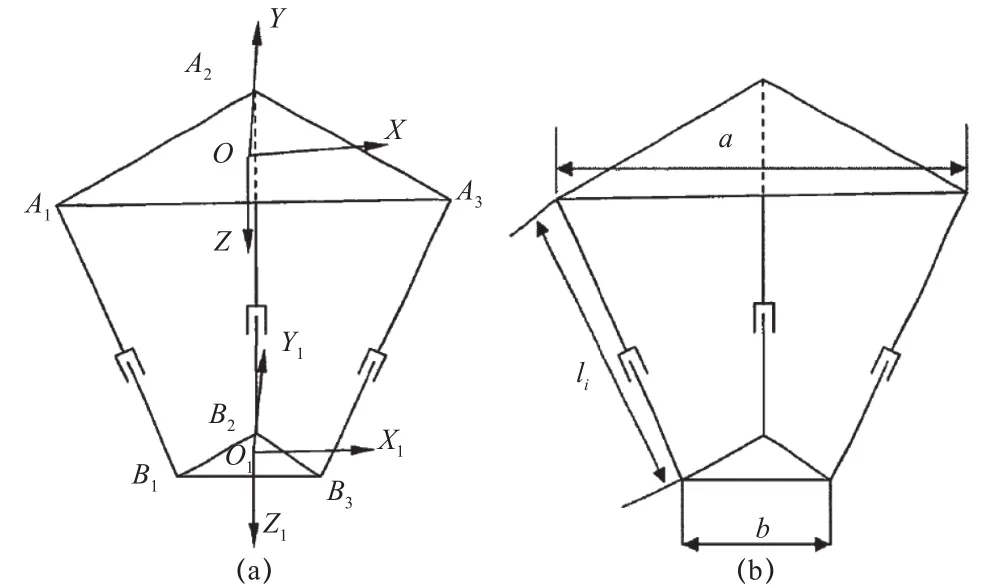
图1 机构简图
对该机构进行静力学分析首先要确定的是驱动与载荷在受力平衡时的联系,以此求解出并联机构的雅可比矩阵进而求出其刚度矩阵,该过程是并联机构结构设计的前提。
1.1 并联机构雅可比矩阵求解原理
并联机构驱动力与外载荷之间通过一个矩阵J0相联系,该矩阵为力学雅可比矩阵。而本文求解该矩阵的公式采用的是虚功原理。
1.2 静力学逆雅可比矩阵求解
依照虚功原理, 当3-TPT并联机构处于平衡的状态时,其所有外力所做的功经过虚位移为零。同时,由于并联机构本身机构的限制,其动平台只能做平移运动,所以作功也只能在其支链轴向上,由此即可得出并联机构静力学雅可比矩阵。由
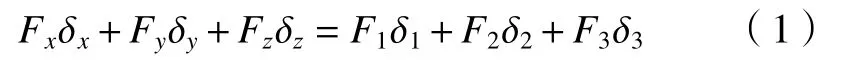
式中: δx、 δy、 δz是外负载下的虚位移; δ1、 δ2、 δ3是支链在外负载下的虚位移。
经推导可得驱动与外负载的关系可表示为

求其逆解则需要

故其逆矩阵得

其中:c=a-b,之后因其力学雅可比矩阵为速度雅可比矩阵的转置可得J0=JT,故J0-1=J-T,基于此公式可继续求解支链刚度。
1.3 并联机构刚度矩阵的原理
Gossilin C[12]提出并建立并联机构的刚度矩阵,其将机构所受负载与其微小形变联系在一起,故被叫做并联机构的刚度矩阵。
该矩阵是依据主动部分的弹性模型来推理的。其表达式为 ΔFl=KlΔl,其中 ΔFl为给予支链的关节力,Kl为刚度矩阵, Δl为关节变量l的改变量。之后推得

式中: ΔF为并联机构末端所受的外负载; ΔX为末端受力产生的形变。
于是,可以得出J-TKlJ-1即为并联机构的刚度矩阵,表达为:K=J-TKlJ-1,Kl为支链刚度矩阵,结构形式为

式中:kii为i杆沿支链轴向的刚度。
1.4 并联机构刚度模型建立
基于输出位置的位姿不同,使得外力作用下机构每个部分发生位移形变不同,如何分析该变化是分析整个机构刚度特性的目的。同时考虑到许多影响并联机构刚度的变化原因,所以本文所做的讨论分析均假设在理想的内外部条件下:(1)不计静平台受外负载时产生的形变。(2)不计各组成部件的重力等次要影响。(3)不计温度、压强等各种外界环境因素。
通过上述分析可得逆雅可比矩阵为

以此可得机构静刚度矩阵为
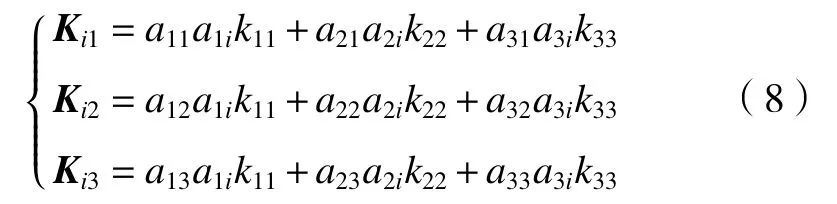
式中:Ki1、Ki2、Ki3为刚度矩阵K中的元素,对机构中其余参数已知时,整机的刚度度矩阵K便可得出。
2 机构支链与整机的刚度求解
2.1 支链刚度求解
并联机构的支链刚度求解是机构刚度矩阵求解的重要组成部分。由于支链的结构组成包括主动部分、被动部分和杆件,具体结构如下图2所示,使得对支链刚度的求解,变成对上述3部分的求解。同时由于支链的结构分布,使得其轴向刚度是主要的刚度因素。
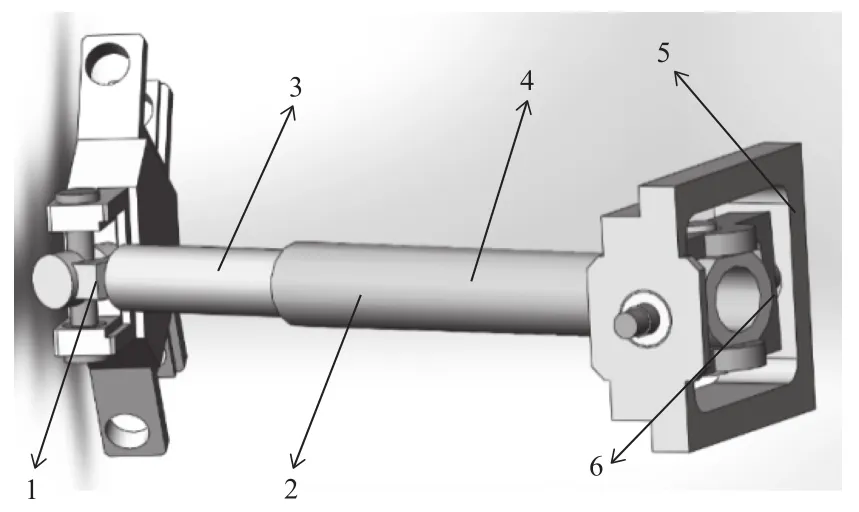
图2 支链结构图
(1)主动部分轴向刚度数学模型分析。在支链的构成中,驱动力由主动部分提供,以滚珠丝杠为主要驱动形式。采用丝杠驱动是因其具有优秀的刚度特性,而且可通过事前加压使滚珠产生斥力,使得整体的刚度变大。
从结构组成上来说,以丝杠、滚珠螺母,支承轴承以及螺母和轴承支架的刚度(分别表示为KS、KN、KB、KH)组成支链的轴向刚度。以K2表示主动部分的轴向刚度,上述单位均为N/μm,则K2计算如下。①丝杠的安装情况决定其轴向刚度,考虑到支

链的结构,该处的丝杠为一端固定安装。丝杠的刚度Ks可按如下式计算。

式中:A为 丝杠的螺纹小径的面积为 2.826×10-4mm2;E为碳钢的弹性模量值为 2 06GPa ;La为载荷作用点到支承的长度,设为300 mm。将上述各数值代入式(10)中得:KS=485130N/mm。
②对螺母刚度的分析,因其内外结构不一,所以理论上将它作为一个内部受压的厚壁圆筒来处理,并且对所涉及的丝杆和螺母要求具有相同的弹性模量、泊松比。则根据国标对于滚珠螺母轴向静刚度的公式得

其中:滚珠的有效圈数为i,该处取为5;丝杠的导程为p,取为5 mm;接触角为 α,取为15°;螺母上接触点处的直径为Dc,取为40 mm;螺母的外径为D1,取为50 mm。最终代入得:KN=418181.20N/mm。
因为轴承为标准件,使用时按照设计要求选用,其刚度性能均已知,故不作分析。同时,螺母支架及轴承支架对结构本身影响较小,故忽略不计。因此,该并联机构主动部分刚度:K2=224587.32N/mm。
(2)被动部分轴向刚度数学模型分析。该部分的主要刚度是虎克铰的刚度,其包括轴承座、轴承和转轴三者的刚度。轴承座所在位置,使其受挤压而发生微小形变,所以在一般计算时,可不计轴承座变形的产生的影响。同时轴承也为标准轴承,其本身对被动部分的刚度同样不计。所以总的来说故转轴的变形是导致支链轴向刚度变化的主要原因。
因为3-TPT并联机构各部件的分布,使得每个支链都可视作圆柱状的二力杆,同时因虎克铰结构的影响,使其仅传递扭矩,这也就导致虎克铰的转轴在受到外负载时会产生弯曲变形。为便于分析,假设在转轴所加负载为集中力,使得其每个作用点都为中心位置。故通过上面的分析,可以得出支链轴向所受力产生的形变可采用二力杆最大挠度公式得

其 中 : ωa、 ωb分 别 为 虎 克 铰1、 5的 形 变 , ω1、 ω2、ω3、 ω4分别为虎克铰 1、 5转轴的挠度变量,l1、l2、l3、l4为轴长度,I1、I2、I3、I4为轴的惯量矩,其中轴看作是圆柱体,分别利用求得两个虎克铰的轴向刚度K1、K5分别为

(3)杆件部分轴向刚度数学模型分析。支链上的杆件分为连接主动部分与动平台虎克铰和静平台两种杆件。因杆3起支撑作用,故为实心圆柱,而杆4内部由于滚珠丝杠的存在,使得其结构为中空圆管状。
对该支链进行受力分析可知,其受轴向力,因此,这也就导致其产生的形变是由受力产生压缩导致的。而对此刚度的计算,可参考直杆轴向拉压变形所产生的刚度公式来计算:

其中:杆3的直径为d3,杆3的长度l3。同理杆4的刚度为K4=965075.22N/mm。
所以经过上面的分析计算可得支链主动部分、被动部分和杆件轴向刚度为:

通过对所求得的各个部分的刚度数值进行分析,发现对各支链的刚度影响最大的是主动部分的刚度,虎克铰刚度对被动部分刚度的影响较小,同时也可以看出静平台虎克铰刚度在整体刚度中占比适中和杆件部分虽刚度较大,但其在整条支链刚度中占比较小。
综上所述,该并联机构支链刚度矩阵为

该矩阵主对角线所对应的3个元素为3条杆件的直线刚度,同时由于在进行并联机构设计时,会将支链长度设置为要求的最小值,以保证在机构在受外力导致支链长度发生变化,引起刚度变化时,能满足各个运动状态的刚度需求。基于此可对支链受力形变时所产生的变化进行分析并进一步分析完整机构的受力形变。
2.2 并联机构整体刚度求解
由于分析并联机构整体刚度的复杂性,使得仅能通过其逆雅可比矩阵来进行分析,但该矩阵不是固定的,是随机构的运动轨迹而发生变化。所以,为得到并联机构的整体刚度矩阵,须将运动轨迹中的某具体点来代入计算,基于此来计算该点的刚度矩阵。
由于机构在Z方向的运动范围为(608.28,1 081.67),以该范围选定Z轴两个轨迹极限运动点A(400, 180, 108.67)、G(0, 0, 608.28),为防止出现特殊性,再任选轨迹内一点M(20, 90, 800),基于此3点来求解机构整体刚度矩阵。点A的逆雅可比矩阵为

以此得到输出端运动到A点时的刚度矩阵为

同理,点G的逆雅可比矩阵与刚度矩阵分别为
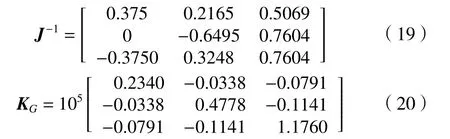
同理,点M的逆雅可比矩阵与刚度矩阵分别为

通过对上述位置点的求解分析可以得出如下结论:
(1)当机构输出端运动到不同位置时,其各个位置对应逆雅可比矩阵和刚度矩阵均有所变化,所以想利用矩阵的数值来分析机构刚度矩阵的变化规律比较难。
(2)当机构受负载,导致输出端位置产生变化,不能单纯的依靠机构的刚度矩阵,还需要将末端外力向量,代入形变公式,求解出输出的形变。
(3)对机构的运行轨迹在Z轴上时,通过对3点的分析可以发现,机构刚度矩阵的主对角线元素明显大于其他元素。
(4)以3点做对比得出,当工作点在Z轴极限位置由小到大时,主对角线上的最后一个元素也是由小到大。
3 结语
并联机构的发展受制于各种因素,而没有蓬勃发展,而本文从刚度入手,利用刚度矩阵法,对3-TPT并联机构进行分析,以此来探索并联机构的发展途径。首先通过雅可比矩阵,得到外力与驱动力的关系,然后建立刚度模型,分别对并联机构的支链和整体进行了刚度的求解分析,并通过上述分析,得到以下结论:
(1)通过对支链轴向刚度与其刚度矩阵分析求解,发现对各支链的刚度影响最大的是主动部分的刚度,虎克铰刚度对被动部分刚度的影响较小,同时也可以看出静平台虎克铰刚度在整体刚度中占比适中和杆件部分虽刚度较大,但其在整条支链刚度中占比较小。
(2)同时由于在进行并联机构设计时,会将支链长度设置为要求的最小值,以保证在机构在受外力导致支链长度发生变化,使得刚度变化时,能满足各个运动状态的刚度需求。
(3)对该并联机构工作空间上的3个点进行实际求解,发现当末端所受外力确定时,末端的受力变形随着x、y、z坐标的增大而减小。但对受力点坐标与刚度的关系并不能清晰的表示出来。
