由一道概率统计试题引发的命题探究与思考

湖南 刘仲喜

高中数学课程应力求通过各种形式自主学习、探究活动，让学生体验数学发现与创造的历程，发展他们的创新意识.但在具体的教学实践中，这一理念往往被形式化.由于情境与问题的封闭性，会使学生提不起探究的兴趣，即便完成了学习目标也不能获得探究的愉悦感.探究需要问题，而问题的产生则来源于兴趣和发现；探究需要方法，而方法需要经验.

一、问题呈现

笔者学校高二阶段考数学试题命制时，笔者设计了如下一道试题：

【题目】甲、乙两人进行投篮比赛，要求各投篮2次，并约定按最后的结果获胜者每多投进一球，对方就要付给他5元钱.已知甲、乙两人每次投中的概率分别为0.8，0.6.

试求：(1)事件A“在甲第一次未投进的条件下，乙获胜”的概率；

(2)甲赢得的钱数X的数学期望.

解析：(1)事件A包含事件B“甲第二次未投中，乙至少投中一次”和事件C“甲第二次投中，乙投中两次”，且事件B与C互斥.

故P(A)=P(B)+P(C)=0.2×(1-0.4×0.4)+0.8×0.6×0.6=0.456.

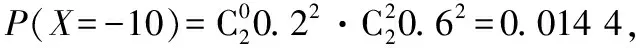
故X的分布列为

X-10-50510P0.014 40.134 40.390 40.358 40.102 4

所以数学期望E(X)=(-10)×0.014 4+(-5)×0.134 4+0×0.390 4+5×0.358 4+10×0.102 4=2.

此题的立意非常好，较贴近现实生活，按常规的方法计算量比较大，但数学期望的值十分简洁干脆，其中是否蕴含着某种显而易见的结论或者规律呢？从而引起了笔者的关注与思考，接下来笔者进行了一番探究.

二、问题探究

探究一：E(X)=2是否有意义？

E(X)=2这个结果充满了惊喜！那么它究竟有没有特殊的意义呢？为了探究这个问题，笔者根据生活的经验对原题的比赛规则:甲、乙各投篮2次，并约定按最后的结果获胜者每多投进一球，对方就要付给他5元钱(下称规则1).作出了如下两种假定(依次称规则2与规则3)：

规则2：让甲先投两次，每投进一球，乙付给甲5元；再让乙投两次，每投进一球，甲付给乙5元.那么按这个比赛规则，甲赢得钱的数学期望E1=5×2×0.8=8(元)，甲输钱数的数学期望E2=5×2×0.6=6(元)，因此，甲赢得钱数的数学期望E(X)=8-6=2(元)；

规则3：甲乙各投球一次算一局，结算后再进行下一局.按这个规则，甲每一局赢得钱数的数学期望E0=-5×0.2×0.6+0×(0.2×0.4+0.8×0.6)+5×0.8×0.4=1

要求每人投两次，故甲赢得钱数的数学期望E(X)=2E0=2.

这样一来，无论是规则2还是规则3，似乎E(X)=2的意义都简洁明了，甚至无需证明就可以接受规则3与规则1是等效的.然而计算简洁的规则2和它们等效吗？

探究二：三个规则是否是等效的？

为探究这个问题只需将题目的条件作一般化处理:设甲乙两人每次投中的概率分别是p,q.

按规则2：E(X)=5×2p-5×2q=10(p-q)，

按规则3：E0=-5(1-p)q+0·[(1-p)(1-q)+pq]+5p(1-q)=5(p-q).

故E(X)=2E0=10(p-q).也就是说规则2与规则3是等效的.而按规则1则有

因此这三个规则是等效的.显而易见规则2更为简洁明了.那么这个结论能否推广？

探究三：尝试将此结论推广

为了探究将此结论推广，笔者继续变换题目中的条件：“每人各投两次”改为“甲、乙各投三次”，分别按三个规则计算得：

按规则2：E(X)=5×3p-5×3q=15(p-q)，

按规则3：E0=-5(1-p)q+0·[(1-p)(1-q)+pq]+5p(1-q)=5(p-q).

故有：E(X)=3E0=15(p-q).

按规则1：

或者改为“甲投两次，乙投三次”.分别按三个规则计算三个规则的结果仍然是相同的！

由此可见这三个规则总是等效的.那么根据规则2可得到一个重要结论:

甲、乙两人进行投篮比赛，要求各投篮n次，并约定按最后的结果获胜者每多投进一球，对方就要付给他A元钱.已知甲乙两人每次投中的概率分别为p,q，那么甲赢得钱数X的期望E(X)=nA(p-q).

甚至是更一般的结论：

甲、乙两人进行投篮比赛，要求甲投篮n次，乙投篮m次，并约定甲每投进一球，乙要付给他A元钱，乙每投进一球，甲要付给他B元钱.已知甲、乙两人每次投中的概率分别为p,q.那么甲赢得钱数X的期望E(X)=nAp-mBq.

从组合数学的角度来看，便可以轻松地得到如下的公式:

限于笔者的学识，不能断定这两个公式在组合数学有无用处，但它们的结果简洁优美而且上述推理的过程又是如此的直观，是值得让人惊叹的!最后回到原题的情境，假设现在乙发现这样的比赛并不公正，提出要求修改比赛规则，那么又应该如何修改呢?

探究四：怎样制定公正的规则？

所谓比赛公正，用数学的观点来看是概率均等或者是期望相等，就此题来看当然就是指期望相等.在现实生活中通常可以从两个角度来调衡：方案一:乙投球的次数比甲多；方案二：乙投进的每个球甲多付一些钱.根据上面得到的结论，若按方案一可调整为：甲投三次而乙投四次；若按方案二可调整为：甲每投进一球，乙付给他3元，乙每投进一球，甲付给他4元.这与我们生活中的经验是一致的，可以看到数学在生活中的应用.

三、关于探究的思考

根据新的《普通高中数学课程标准(2017年版2020年修订)》的基本理念“倡导积极主动、勇于探索的学习方式”的要求，高中数学课程应力求通过各种形式自主学习、探究活动，让学生体验数学发现与创造的历程，发展它们的创新意识.但在具体的教学实践中，这一理念往往被形式化：教师根据教学内容设置相应的情境，接着由教师或学生提出一些猜想或问题，然后引导学生讨论探究，尝试解决问题，最后总结归纳形成结论.这样的教学有助于培养学生的探究意识，然而由于情境与问题的封闭性，会使学生提不起探究的兴趣，即便完成了学习目标也不能获得探究的愉悦感.如何从教学的实践与现实的生活中去挖掘可以值得探究的数学问题，以更加开放的形式来引导学生进行自主探究学习也许是每个数学教师面临的一个崭新课题.首先，探究需要问题，而问题的产生则来源于兴趣和发现.如在进行上面的探究之前，笔者是因为发现运算的复杂性和结果的简洁性而产生了浓厚的兴趣，是出于对简洁美的追求，或者说是一种信念“凡是简洁的都必定是具有和谐之美”.而这样的素质正是非智力的因素的范畴，是我们现实的数学教学中需要大力倡导的.作为一名教师发现学生最需要的能力就是发现和提出问题的能力，如果某个学生能够发现和提出一个新颖的有价值的问题常常会让人觉得欣慰与赞赏；其次，探究需要方法，而方法需要经验.如在进行上面的探究过程中笔者将原题的规则与生活的经验相结合，从不同的角度来思考得到简洁的方法.俗话常说“穷人家的孩子会读书”不是没有道理的，因为穷人家的孩子有更多的实践经验.