从一道高考题看三角恒等变换的处理技巧

山东 周梦鸽

三角恒等变换是高考中的重要考查内容，主要考查学生对两角和与差的正弦、余弦、正切以及二倍角等基本公式的运用，同时也要求学生掌握一定的处理技巧，方便运算.往年的高考题目中，对三角恒等变换的考查有出现在选择题或填空题中，考查公式的正用、逆用或三角函数化简、求值、求角等，也有出现在解答题中，与三角函数或解三角形知识相结合.其中，三角恒等变换的处理技巧一直是学生学习的难点，它对学生的思维量、灵活性、数学核心素养提出较高要求.又因为它在高考试题中排序靠前，很多学生在处理条件时因为研究方向不对存在无从下手或者无头乱撞的情形，在高考考场上可能会耗费大量时间，影响发挥.本文将从一道高考真题入手，对三角恒等变换的部分技巧进行总结归纳，以此希望为学生备考本章节内容提供些许启发与参考.

一、试题展示及分析

二、教材原型

高考真题在课本练习题中往往是有迹可循的.山东省已经实施新高考两年，重在考查学生的基本知识、基本思想和基本技能，配套使用的数学新教材在导语中也对学生提出要求——要“重视基础、拾阶而上”，这也恰恰是高考试题命制时的一个依据.对此，比较重要的一个体现就是课本题改编几乎每年都会出现在高考试题中.本题就是必修一教材练习题中的两道证明题的变式.

方法介绍：在解决证明等式恒成立问题时，一般可以从左往右、从右往左或者左右两端同时化简到同一形式入手，遵循的原则是“由繁到简”，即从复杂的一端往简洁的一端进行化简.

证明过程：

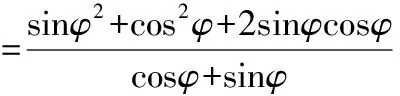
=cosφ+sinφ=右边.

证毕.

本题中涉及的知识有“1”的变换和二倍角正弦公式的使用，与高考题所求式子高度相似，可以为高考题中所求代数式的处理提供解决方案.

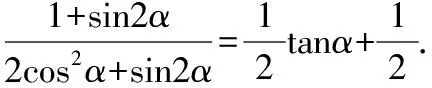
证明过程：

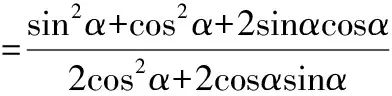
证毕.

本题中涉及的知识有“1”的变换和一次齐次式化切的办法，同样与高考题中所求式子非常相似，为学生解决此类问题提供思路.

以上两道课本题目与高考题目中所求式子相差无几，这启发学生在平时的学习过程中一定要注重课本习题的掌握，牢记基础知识，在复习时，要回归课本，善于总结知识方法.

三、解法探究

方法一：特殊值法

选择其中一种情况将其代入所求代数式

故选C.

方法二：构造齐次式

故选C.

说明：此方法是观察到分子分母的次幂不同，由此将其拆解成两部分，一部分是一次齐次式，另一部分是“1+sin2θ”，又通过对“1”进行替换，“sin2θ”进行升幂缩角变成二次多项式，再配凑了一个分母“1”即“sin2θ+cos2θ”，构造出一个二次齐次式.两个齐次式依次除以cosθ，cos2θ，最终将所求式子化成只含有tanθ的式子，代入求值即可.

齐次式化切是三角恒等变换的高频考点.利用齐次式化切也是给出角的正切值去求正弦、余弦混合的代数式的值这类问题的常见解法.它的好处在于不需要求解角的正弦值和余弦值就可得到最终结果，计算量少，但对于式子的处理和预判要求较高.常见的题型有三类：一次齐次式型、二次齐次式型和配凑型.所谓齐次式就是分子分母每一项次幂相同，它的处理办法是：对于一次或二次齐次式，分子分母同除以cosθ或cos2θ得到只含有tanθ的式子；对于非齐次式，需要配凑出齐次式再化成含正切函数的式子，在配凑的过程中利用1=sin2θ+cos2θ将整式配凑成分式或者将实数变成二次多项式.

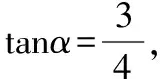
答案：A

方法三:“1”的巧用

=sinθ(sinθ+cosθ).

接下来可利用方法一带值计算，也可构造二次齐次式进行计算.

说明：此解法对应教材中习题对于“1”的处理，在这里学生要熟悉“sinθ±cosθ”与“sin2θ”的联系，即(sinθ±cosθ)2=1±sin2θ.因此观察分母和分子中出现的“1+sin2θ”，可以化简所求式子.

“1”的巧用之一已经体现在上述当中，即依据同角三角函数的平方关系进行替换.除此以外，在余弦二倍角公式cos2α=2cos2α-1=1-2sin2α中也有“1”的出现，选择适当的二倍角公式可以快速得到想要的结果，下题便是很好的体现.

答案：2

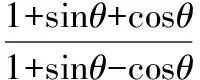
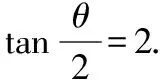
本题中等式左端分子分母各出现了一个“1”，使用的公式却不同，原因在于后面cosθ前的符号不同，但解题的思想是一致的，即利用余弦二倍角公式中出现的“1”来消掉题干中的“1”，这又是“1”的另一巧用.

四、结束语

三角恒等变换在高考试卷中属于难度中等、较为基础的题目，但它又常与解三角形和三角函数等内容相结合，因此是解决这一模块内容的一根纽带.它主要考查学生数学运算和逻辑推理的数学核心素养，需要学生准确掌握同角三角函数的基本关系、和差公式以及倍角公式，同时能够灵活运用解题技巧快速解决问题.在备考过程中，学生应重视本章节的内容，加强计算，扎实掌握各种处理技巧，合理预判问题走向.