当韦达“套路”遭遇“卡壳”的破解策略——以一道椭圆求斜率比值为定值问题为例

四川 张 兵 杜海洋

在解析几何解题教学中，直线与圆锥曲线联立时，韦达定理套路策略高频出现，但也常常遭遇“卡壳”．通过剖析一道圆锥曲线综合试题“套路卡壳”原因，以探索为契机，达到解决这类问题的“新套路”目的．

高三模拟试题中出现一道看似常规的解析几何综合试题，题目设直线方程为x=ty+1时，发现部分学生不能套用韦达定理而“卡壳”；有学生提出如设直线方程为y=k(x-1) 时，是否可以避免出现非对称韦达，认为是题目设置直线方程有“诱导”之嫌，但动手去做时，却再次被“卡壳”，说明出题者在两条道路上都设置“关卡”，运用常规方法到底 “卡”在哪儿？如何化解这道“关卡”？有没有解决这类问题 的“新套路”呢？下面笔者还原这道试题解答过程.

一 、试题呈现

(1)求C的标准方程；

(2)设直线BM，AN的斜率分别为k1，k2，若k2=λk1，证明：λ为定值．

本试题考查了椭圆的标准方程、几何性质、直线与椭圆的位置关系以及定值问题.考查了设而不求，化归与转化等数学思想方法，检验了运算求解、分析问题与解决问题的能力，试题解法多样，平中见奇，内涵丰富，为不同学生搭建了施展才能的舞台，是一道具有研究性学习价值的好题.

二、试题求解过程

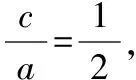
第(2)问：证法1:

可得(3t2+4)y2+6ty-9=0，

又A(-2,0)，B(2，0)，所以

将y1，y2代入①得

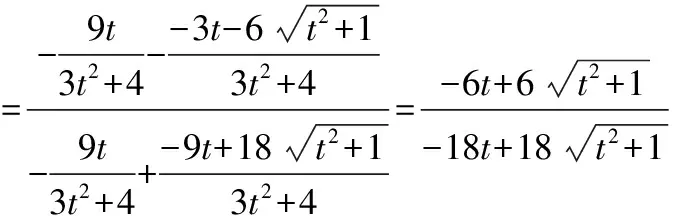
由于有证法1的思维启迪，班上学生1提出他的想法：是否可以消掉一个变量保留两个变量，然后分子分母也可进行整体约分.

证法2:

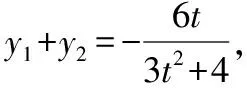
证法3:

证法4：

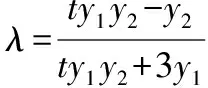
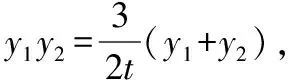
证法5:

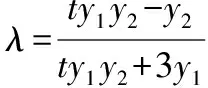
证法6:

就在此时班上一名学生4谈到此题后续不能继续运用韦达定理是否是出题者提前设置的“坑”，即问题出现在直线方程x=ty+1的设法所致，本题明显可以用点斜式表示直线方程，只是需要分类讨论一下直线l斜率存在情况，后续或许直接可以用韦达定理，话音一落，大家动手解答如下：

当直线斜率k存在时，设直线l的方程为y=k(x-1)，

可得(3+4k2)x2-8k2x+4k2-12=0，

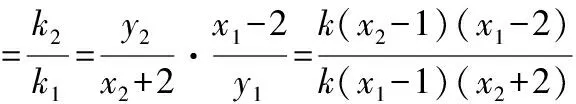
到此时发现所得式子结构形式更加复杂，但好在有前面证法2为铺垫，大家很快想到消参，

证法7:

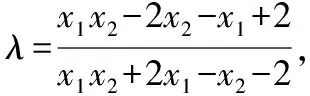
则(λ-1)x1x2+(2λ+1)x1+(2-λ)x2-2λ-2=0，

证法8:

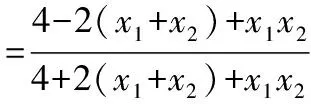
三、解题反思

1.从以上解答可以体现出每种证法在思维上的层层递进，符合学生认知的最近发展区，当遇到新问题出现“卡壳”时，解答思维应回归“原点”，尤其证法1虽运算难度大，但思维最“实惠”.

2.探究破解方法始终围绕问题的本质“消元”，即多元变减元，逐步达到局部代换或整体代换.

3.解答过程应以学生的想法为根本，尊重学生、让学生的思维得以施展，真正把解题教学落实课堂，体现学生是课堂中真正的主体，而不是靠老师提供的“简洁”“妙解”，甚至“秒杀”，达到捷径，那样其实并没有展示其中的本质．

四、总结提炼