粗糙元对零攻角尖锥模型高超声速边界层转捩的影响研究

2022-08-30成江逸司马学昊

南京航空航天大学学报 2022年4期

成江逸，司马学昊，吴杰

（华中科技大学航空航天学院，武汉 430074）

临近空间高超声速飞行器是当前的研究热点，其具有机动性高、飞行轨迹难以捕捉及预测等特点。但是，较之常规弹道式高超声速飞行器，临近空间飞行器飞行的高度低、空气密度大，随之而来的便是飞行器热防护问题。高超声速飞行器在大气层内以高超声速飞行时湍流边界层的热负荷与摩擦阻力可达层流边界层的3～5 倍［1］。因此，维持高超声速飞行器表面的层流区域是高超声速飞行器降热减阻的重要途经之一。高超声速边界层转捩分为主动控制与被动控制。主动控制方法需要向流动施加能量，目前有壁面吹吸以及等离子激励等，但由于其对应的控制机构复杂，在飞行工况下能量输入需求大，效用相对较低。相较于主动控制技术，被动控制技术机构简单、无需能量输入，容易在飞行器上实现，常用边界层转捩被动控制方法包括超声波吸收材料、波纹壁、槽道以及粗糙元等［2］。在诸多边界层转捩被动控制手段中，粗糙元通常会促进高超声速边界层转捩，并定义，临界粗糙元为开始影响层流转捩的粗糙元大小，有效粗糙元为立即引起层流转捩的粗糙元大小［3］。早在1959 年James［4］在带粗糙元条带的空心圆柱自由飞行实验中发现了边界层转捩延迟现象。1964 年，Holloway 与Sterrett［5］在风洞平板实验中发现在特定粗糙元及一定来流情况下，转捩起始点被延迟。2006年，Fujii［6］在Ma7.1尖锥实验中发现粗糙元延迟转捩起始点，且还发现微波浪纹壁与等效三维球体粗糙元效果相同，转捩起始点与流场波动谱差别不大。

近期Zhong［7-21］团队开展了大量粗糙元对高超声速边界层不稳定性的研究工作。2010 年，Duan等［7］在验证高阶切割单元数值模拟时，偶然发现表面粗糙元延迟了平板层流边界层转捩起始点。而后，他们接着使用直接数值模拟探究了粗糙元高度、粗糙元位置、粗糙元宽度、多粗糙元及间距等粗糙元各参数对边界层转捩的影响。研究发现，粗糙元只有在位于特定第二模态不稳定波的同步点下游时才可能延迟边界层转捩，其次还发现低于当地边界层高度的粗糙元延迟了边界层转捩，并且粗糙元高度越高，抑制无量纲压力幅值效果越好［7-12，16］。粗糙元宽度未展现明显效果［13，16］。多粗糙元研究结果表明，当粗糙元间距为10 倍粗糙元宽度左右时，多粗糙元抑制无量纲压力幅值效果最好，且多粗糙元效果优于单粗糙元效果［13，16］。Mortensen 和Zhong［12］还考虑真实气体模型以及热化学非平衡，通过数值模拟发现，相较于理想气体模型，粗糙元对第二模态不稳定波幅值的抑制效果在真实气体模型里更有效。在高超声速边界层转捩中，Mack第二模态不稳定波占主导作用［22-23］。由于粗糙元的存在，会在边界层内，粗糙元前后产生分离区。在流动分离区附近的第二模态不稳定波无法进入分离区，只能在声线与分离区之间的被分离区压缩了的区域反射传播［24］。通过Miles 定律，这种反射会导致幅值降低，从而抑制了第二模态不稳定波发展。Haley 和Zhong［17］认为抑制作用程度大小取决于分离区大小，在数值模拟带粗糙元尖锥情况下，后分离区大小明显小于平板粗糙元后分离区大小，但其对第二模态不稳定波的抑制作用仍可与平板情况下的相比较。由于可能是数值模拟计算二维平板与三维尖锥所带来对分离区大小相差较大的问题，因此认为分离区对第二模态不稳定波的影响仍然有待探究。国内周云龙［25］使用直接数值模拟方法研究了粗糙元3 种外形对流场的影响，发现矩形粗糙元抑制效果最好。

现阶段在探究粗糙元对高超声速边界层影响时，主要使用直接数值模拟方法，加入的扰动频率单一。但自由来流情况下，来流扰动的频率呈离散式分布；并且，数值模拟的边界条件设定也往往与风洞实验存在差异。因此，仅依靠数值模拟方法探究粗糙元对边界层转捩的影响仍存在较大难度。针对以上问题，本实验研究尝试探究粗糙元对边界层不稳定波发展以及转捩过程的影响。

1 实验平台与实验模型

1.1 实验平台

本次风洞实验依托华中科技大学Φ0.25 mMa6 Ludwieg 管风洞［26］，如图1 所示。该Ludwieg管风洞由双U 形高压长直储气段、快开阀、Laval 喷管、实验段、扩张段以及真空罐等主要部件组成。风洞的高压储气段与Laval 喷管通过快速控制阀门分开。在风洞启动前，储气段内储存着高温高压空气，控制阀门下游的部分则通过真空泵抽成了真空。在开启快速控制阀门的瞬间，会产生一系列的非定常膨胀波，该膨胀波以声速向储气段的上游行进；该膨胀波驱动管内的气体达到储气段启动马赫数。当膨胀波以当地声速到达储气段尾端后，再次被反射回来。当反射膨胀波到达快速控制阀时，快速控制阀门关闭，风洞的运行结束。与此同时，在快速控制阀的下游，受压差驱动，气流在Laval 喷管喉部形成声速流，并沿着Laval 喷管膨胀加速，在试验段时获得对应设计马赫数的高超声速气流［27］。该风洞建设完成于2020 年并试车成功，风洞单车次有效运行时长约116 ms［26］，如图2 所示储气段与实验压力测量数据。归一化Pitot 压力脉动结果显示该风洞的流场品质较之不伦瑞克大学HLB 与美国空军学院HHK-6 风洞更优［26，28］，如图3 所示。

图1 Φ0.25 m Ma6 Ludwieg 管风洞[26]Fig.1 Φ0.25 m Ma6 Ludwieg tube wind tunnel[26]

图2 有效运行时长[26]Fig.2 Effective running time[26]

图3 归一化Pitot 压力脉动均方根值比较[26,28]Fig.3 Comparison of normalized Pitot pressure pulsation RMS values[26,28]

1.2 实验模型

本次实验所使用7°半锥角光滑尖锥模型，模型全长0.4 m，尖锥头部钝度为50 μm。模型材质为不锈钢，共分为4 段，表面粗糙度为Ra3.2（壁面法向上的点与壁面基准线之间距离绝对值的算术平均值小于3.2 μm），如图4 所示。其中数字黑点代表PCB 孔位及相应编号，第一个PCB 孔位距顶部182.6 mm，后面除3 号与靠后的4 号孔位间隔约30 mm，其余均相间24.8 mm（约25 mm）。由于PCB 数量有限，部分PCB 孔位未安装PCB 而是使用相应尺寸堵头封闭。

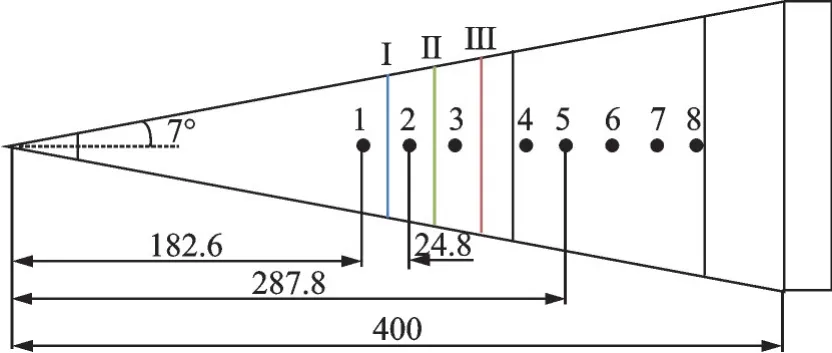
图4 光滑尖锥模型与粗糙元条带布置示意图Fig.4 Smooth sharp cone model and roughness strip layout

在粗糙元布置方法上，本文借鉴了Fong［16］在裙锥上设计粗糙元的方式，在光滑尖锥表面上粘贴一圈固定厚度的粘胶获得本实验所使用的粗糙元尖锥模型。实验所使用的粗糙元宽度与厚度均分别为2 mm 与0.5 mm。本次实验共有3 处选择性放置粗糙元条带，分别用大写罗马数字表示，如图4 所示。Ⅰ处粗糙元条带位于1 号与2 号孔位中间；Ⅱ处粗糙元条带位于Ⅰ处粗糙元条带后方25 mm；Ⅲ处粗糙元条带位于Ⅱ处粗糙元条带后方25 mm。

1.3 压力传感器

实验使用的高频压力传感器为PCB132 系列，如图5 所示，用于测量模型表面的压力脉动。传感器的有效动态响应范围为10～1 000 kHz，量程为345 kPa，可以分辨的最小压力为7 Pa，传感器的固有频率大于1 MHz。本次实验所使用的PCB 高频压力传感器敏感性系数分别为：160.4、123.0、148.5、135.3、138.9 和143.8 mV/psi。

图5 PCB132 系列高频压力传感器Fig.5 PCB132 series high frequency pressure sensor

实验使用数据采集器采集压力传感器测得的信号。所有传感器的输出信号由Spectrum A/D 卡采集，采集系统垂直分辨率16 bit。依据Nyquist 采样定理，采样频率应为所采集信号最高频率的2 倍以实现对信号的精确测量，考虑到高超声速风洞中第二模态不稳定波以及其谐波高达数百千赫，因此实验对不稳定波采集选取的采样频率为3 MHz。

2 实验结果与分析

2.1 数据后处理方法

通过对PCB 采集所得时域信号进行傅里叶积分变换，获得频域信号，即压力脉动功率谱密度（PSD）；通过对相邻PCB 采集所得时域信号进行互相关分析，获得第二模态不稳定波传播速度；通过对PSD 数据进行处理，获取增长率数据，具体的增长率计算公式为［29］

式中：αi为增长率，f为频率，s为两测点距离，A（f）为频率为f时的幅值大小。

通过假设在相邻压力传感器（分别位于sj与sj+1）间增长率为常数，所以中点sj+1/2处的增长率为

式中PSD（f）为频率为f时PSD 数值大小。

2.2 实验结果分析与讨论

2.2.1 单粗糙元条带对不稳定波发展的影响

本节风洞实验探究单个粗糙元条带对第二模态不稳定波发展以及边界层转捩的影响，实验时使用了图5 所示中的1、2、4、5、6 与8 号孔位安装PCB，其余孔位安装孔销封堵。粗糙元条带分别单独布置于Ⅰ处与Ⅲ处。实验储气段总压7 bar，总温350 K，来流单位雷诺数Re∞= 10.71× 106m-1。风洞实验采集数据经傅里叶积分变换处理所得压强脉动密度功率谱结果如图6 所示。

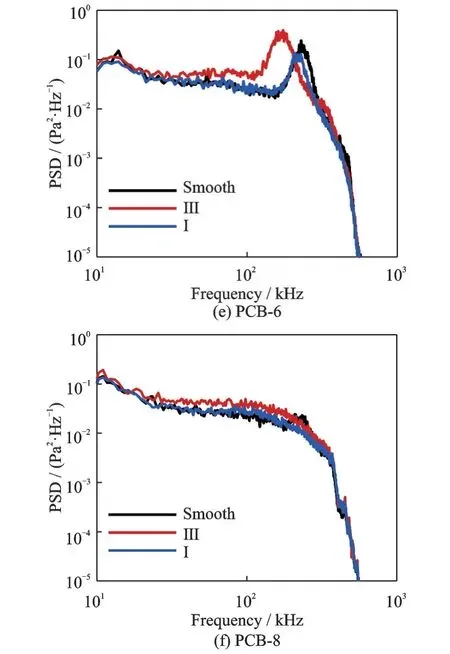
图6 光滑与单粗糙元条带尖锥6 个孔位PSD 结果Fig.6 PSD results of pressure fluctuation along sharp cone with smooth surface and single roughness element

由1、2 号孔位PCB 实验结果可发现，来流在未经过粗糙元时，第二模态不稳定波特征无明显变化，流场与光滑尖锥保持一致，同时也表明本风洞流场的重复性较好。由2、4 号孔位PCB 实验结果可发现，刚经过粗糙元的第二模态不稳定波会发生低频频移且第二模态不稳定波的最大幅值会有所减小。由4、5、6 号孔位PCB 实验结果可发现，在经过粗糙元后，第二模态不稳定波的频移与最大幅值会逐渐趋向于无粗糙元条件下流场结果。同时，也可以发现光滑情况下第二模态不稳定波幅值在5号PCB 孔位附近达到最大并开始衰减，而含粗糙元情况下第二模态不稳定波幅值一直处于增长。可发现粗糙元可延长第二模态不稳定波增长过程。由8 号孔位PCB 实验结果可发现，第二模态不稳定波经历了幅值先增大后减小的过程，最终特征消失，仅光滑情况下第二模态不稳定波特征还稍有表现，可判断粗糙元情况下流动均已湍流，光滑情况下流动即将进入湍流状态。由此现象可见，粗糙元虽然一定程度上可以降低部分频率范围的第二模态不稳定波的幅值，但是其增长率明显高于光滑尖锥情况。

之后，探究了单粗糙元条带对第二模态不稳定波传播速度影响。由于Ⅲ处放置的粗糙元较后，选取的统一对比处为4 号孔位后，由此选择仍可观测到第二模态不稳定波信息的4 号与5 号孔位PCB所获取的信号进行互相关分析，结果如下。如图7所示为4 与5 号孔位PCB 压力传感器信号经过互相关分析得到的曲线。两个PCB 之间间距为25 mm，在光滑、仅Ⅲ处放置粗糙元与仅Ⅰ处放置粗糙元情况下，两测点间的时间偏移量分别为0.034 7、0.034 7 与0.035 3 ms。经计算，得到的相速度约分别为720.5、720.5 和708.2 m/s（分别为91.7%、91.7%和90.1%的边界层外缘速度Ue）。三者差别不大且归一化相速度均符合［1-1/Ma，1］慢模态相速度区间，说明单粗糙元条带仅影响了第二模态不稳定波的幅值与增长率，对第二模态不稳定波波包的传播速度无明显影响。

图7 3 种情况下4 与5 号孔位PCB 压力信号互相关系数曲线Fig.7 PCB pressure signal correlation curves of holes 4 and 5 under three conditions

进一步，对第二模态不稳定波增长率影响进行研究。同样选取4 号与5 号孔位PCB 所获取的信号进行分析。如图8所示为光滑、仅Ⅲ处布置粗糙元与仅Ⅰ处布置粗糙元情况下，4 号与5 号孔位间第二模态不稳定波增长率计算结果。对比光滑与仅Ⅰ处放置粗糙元情况，易发现200 kHz以下频率增长率几乎无差别，而200 kHz以上频率增长率仅Ⅰ处放置粗糙元情况下显著高于光滑情况；对比光滑与仅Ⅲ处放置粗糙元情况，则100 kHz 以下频率增长率差别不大，而100 kHz以上是仅Ⅲ处放置粗糙元情况下的增长率先短暂下降后迅速增长起来并大幅超过光滑情况下的增长率。可能是因为Ⅲ处离4、5 号孔位较Ⅰ处更近，显现出了更为短暂的影响，而显示的Ⅰ处影响则是随流场较长时间后的影响或因为是不同位置单粗糙元对不同段频率有影响，粗糙元越靠后，使受影响最低频率降低。

图8 3 种情况下4 与5 号孔位间第二模态不稳定波增长率Fig.8 Amplification rate of the second mode instability wave between holes 4 and 5 under three conditions

2.2.2 多粗糙元条带对不稳定波发展的影响

本节实验方法和条件2.2.1 节相同，3 条粗糙元分别位于Ⅰ处、Ⅱ处与Ⅲ处。实验粗糙元布置方案分别为仅在Ⅰ处放置粗糙元、在Ⅰ处和Ⅱ处放置粗糙元和在3 处均放置粗糙元条带。实验数据处理后所获得的压强脉动功率谱密度结果如图9所示。

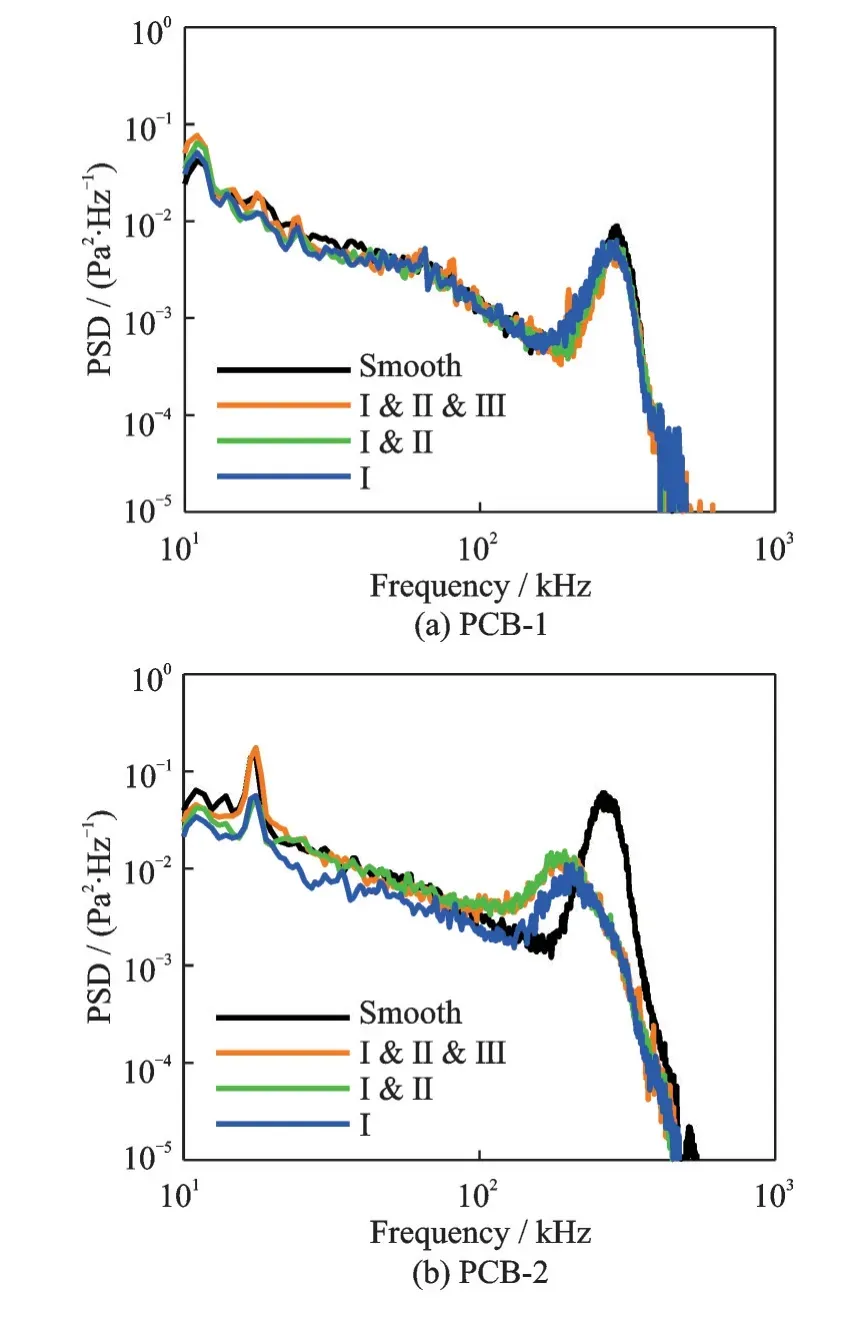
图9 光滑与多粗糙元条带尖锥6 个孔位PSD 结果Fig.9 PSD results of pressure fluctuation along sharp cone with smooth surface and multi-roughness elements

由1、2、4 号孔位PCB 测量结果可知，第二模态不稳定波每经过一次粗糙元条带，都会发生一次低频频移，而最大幅值不变或稍有减小。同样地，由4、5、6 号孔位PCB 实验结果可知，第二模态不稳定波经过粗糙元幅值恢复至不放置粗糙元状态时的位置取决于最后一个粗糙元的位置，越是远离最后一个粗糙元的位置，第二模态不稳定波越靠近无粗糙元情况下的第二模态不稳定波状态。由8 号孔位PCB 实验结果可知，带粗糙元流动已湍流，光滑情况下流动即将湍流。

探究多粗糙元条带对第二模态不稳定波传播速度影响，选取分析段依旧为4 与5 号孔位间，结果如图10 所示，两孔位间距25 mm。由图可知，时间偏移分别为 0.034 7、0.035 3、0.035 2 和0.034 0 ms。经计算，相速度分别为720.5、708.2、710.2 和735.3 m/s（分别为91.7%、90.1%、90.4%和93.6%的边界层外缘速度Ue）。4 者差别不大且归一化相速度均符合［1-1/Ma，1］慢模态相速度区间，说明多个粗糙元条带对第二模态不稳定波波包的传播速度依旧没影响。

图10 4 种情况下4 与5 号孔位PCB 压力信号互相关系数曲线Fig.10 PCB pressure signal correlation curves of holes 4 and 5 under four conditions

之后，研究多粗糙元条带情况下对第二模态不稳定波增长率影响。同样选取4 号与5 号孔位PCB 所获取的信号进行计算，结果如图11 所示。对比光滑与2 处放置粗糙元情况，易发现120 kHz以下频率增长率几乎无差别，而120 kHz 以上频率增长率先减小后增大并反超光滑情况下增长率大小；对比光滑与3 处放置粗糙元情况，80 kHz 以下频率增长率与光滑情况下差别不大，而80 kHz 以上增长率先短暂下降后迅速增长并超过光滑情况下的增长率。现象缘由同2.2.1 节，可能增长率也存在与幅值一样的现象，会恢复至光滑情况下；也可能是粗糙元靠后会使增长率增大的最低频率减小。

图11 4 种情况下4 与5 号孔位间第二模态不稳定波增长率Fig.11 Amplification rate of the second mode instability wave between holes 4 and 5 under four conditions

2.2.3 不同来流情况下粗糙元对转捩影响

为探究不同来流情况下，不同粗糙元布置方法所带来的效果差异，在总压7 bar 的基础上还进行了总压分别为5 与9 bar，总温350 K 的实验，来流单位雷诺数分别为Re∞= 7.65 × 106m-1与Re∞= 13.77 × 106m-1。粗糙元布置方案分别为仅在Ⅲ处布置粗糙元条带与在Ⅰ、Ⅱ和Ⅲ处均布置粗糙元条带。实验PCB 数据经处理后获得如图12所示的功率谱密度图，其中5 bar 情况下仅选取了6与8 号孔位处，9 bar 情况下仅选取了4、5 与6 号孔位处。

首先对比来流总压5 bar 情况下PSD 图。在6号孔位处3 种模型的第二模态不稳定波特征均明显。但在8 号孔位处，3 处均布置粗糙元条带情况下的第二模态不稳定波特征即将消失；同时仅Ⅲ处布置粗糙元情况下的第二模态不稳定波特征也不如光滑情况下的明显。可判断粗糙元情况下转捩结束点将被提前。在这两种粗糙元布置方案中，在5 bar 总压情况下，3 处均布置粗糙元条带相较于仅在Ⅲ处布置粗糙元条带更促进边界层转捩结束。图12（a）中，6 号孔位PCB 的PSD 分布中出现了300～400 kHz 范围的次封值频率可能为第二模态不稳定波的谐波。谐波频率大致为其主频的2 倍。此时第二模态不稳定波频率为140 kHz 和200 kHz左右，而谐波频率在300 kHz 和400 kHz 左右，正好为第二模态不稳定波频率的2 倍。由于谐波幅值相较主频不大，影响不大，因此没有考虑其影响。

图12 5 bar 与9 bar 情况下部分孔位PSD 结果Fig.12 PSD results of partial holes at 5 bar and 9 bar

接着对比来流总压9 bar 情况下PSD 图。在4号PCB 孔位处，仅在Ⅲ处布置粗糙元情况下的第二模态不稳定波特征已经消失，流动经过粗糙元后立即变成湍流状态。在5 号PCB 孔位处，在3 处均布置粗糙元与光滑情况下，第二模态不稳定波特征仍存在，但是在6 号PCB 孔位处3 处均布置粗糙元情况下第二模态不稳定波特征消失，流动状态已经为湍流，而光滑情况下的第二模态不稳定波特征虽不明显了但是仍然存在，流动即将变成湍流。此时，带粗糙元条带情况下流动相较于光滑情况下均提前湍流，并且仅Ⅲ处布置粗糙元条带相较于3 处均布置粗糙元条带更促进边界层转捩结束。

可以明显发现，在5 bar 与9 bar 情况下，仅在Ⅲ处布置粗糙元与3 处均布置粗糙元时，不同布置方案对促进边界层转捩结束程度的比较结果不同。其原因可能在于不同来流情况下，同步点位置发生了改变。在较低单位来流雷诺数情况下，第二模态不稳定波同步点靠后，3 处均布置粗糙元时靠前的粗糙元条带可能会起促进转捩的效果。而在较高单位来流雷诺数情况下，第二模态不稳定波同步点靠前，3 处均布置粗糙元时靠前的粗糙元起延迟转捩的效果。所以，不同粗糙元布置方案在不同来流情况下效果不同，可见粗糙元布置方案对来流情况较为敏感。