壁温比对高速钝锥边界层转捩天地差异的影响研究

姚世勇，段 毅，徐 聪，李思怡，杨 攀，段会申

（空间物理重点实验室，北京 100076）

高马赫数飞行器绕流存在着激波、边界层、流动分离、稀薄气体效应和高温真实气体效应等多种复杂流动现象的空气动力学问题，其中边界层的转捩问题是高马赫数流动研究的热点和难点。当飞行器以高马赫数飞行，边界层从层流状态转捩为湍流状态时，其表面摩擦阻力和表面热流急剧增加，直接影响着飞行器的飞行性能。准确预测边界层的转捩位置将为飞行器设计提供理论依据，可以有效地改进飞行器性能，提高其升阻比，降低燃料消耗，并有利于进行热防护设计，是飞行器设计的关键问题之一。

圆锥作为飞行器的重要组成部分，前人对其边界层在高马赫数条件下的流动稳定性及转捩特性开展了大量的研究［1-8］。作为美国空军研究实验室和澳大利亚国防科学技术组织协同开展的国际性飞行试验研究项目，HIFiRE-1 飞行器采用的是钝度2.5 mm，长1.1 m 的7°半锥角圆锥模型，旨在对圆锥体边界层转捩及激波相互干扰进行研究。Kimmel 等［9］和Li 等［10］对HIFiRE-1 上 升 段 的 边 界层 转 捩 特 性 进 行 了 分 析。 Stanfield 等［11-13］对HIFiRE-1 上升段的激波-边界层干扰和再入过程边界层转捩的飞行数据进行了分析，发现在上升段由于飞行器的动力学运动，其作为飞行试验脉动压力的第二来源并未在风洞实验中出现，飞行器在再入段则经历了第二模态引起的迎风子午线转捩。Wadhams 等［14］对HIFiRE-1 进 行 了 地 面 试 验 转 捩研 究 并 分 析 了 试 验 结 果。 MacLean 等［15］对HIFiRE-1 进行了计算分析并与地面转捩试验结果进行了对比。Alba 等［16］利用线性抛物化稳定性方程对HIFiRE-1 的边界层稳定性进行了分析，结果与在NASA Langley 研究中心马赫6 风洞实验测量的转捩位置吻合很好。Willems 等［17］对大迎角下的HIFiRE-1 边界层转捩进行了实验研究，发现从迎风面到背风面存在明显的条带结构。Juliano等［18］对高雷诺数、大迎角下HIFiRE-1 表面压力脉动特性进行了地面实验研究，结果表明迎风线和背风线上的扰动是由第二模态波放大引起的。

近些年来，关于壁温比对边界层转捩影响的研究，涂国华等［19］指出除了单位雷诺数，壁温比也是引起飞行试验与地面试验转捩天地差异问题的主要因素。Zhao 等［20］开展了总温对零迎角尖锥边界层转捩影响的数值模拟研究，发现随着来流总温的增加，尖锥的转捩起始点后移，转捩区长度减小。刘智勇等［21］研究了温度对高速平板边界层转捩雷诺数的影响，发现在不高于1 000 K 的壁温条件下，扰动的增长与壁温存在一致性的变化规律，并给出了转捩雷诺数与壁温比和N值的函数关系式。此外，Liu 等［22］还对风洞实验与飞行试验转捩数据的天地相关性进行了研究。马祎蕾等［23］开展了壁温对钝三角翼三维边界层的稳定性及转捩影响的研究，揭示了壁温比对不同扰动模态彼此相反的影响规律和在不同位置处的不同影响量值是引起转捩反转的内在机理。

由于地面实验条件无法完全复现天上飞行的实际状态，天地差异客观存在。边界层转捩问题机理复杂，其天地差异呈现新的特点。揭示边界层转捩天地差异的主要机理是开展转捩问题天地相关性研究的基础，是建立相关模型和方法的前提。本文首先对天上飞行状态与地面风洞状态下钝锥边界层的转捩特性进行了对比，然后利用基于线性稳定性理论的eN方法对飞行试验与风洞实验状态下的钝锥边界层进行了转捩预示，最后研究了壁温比对钝锥边界层的稳定性及转捩的影响，揭示钝锥边界层转捩天地差异的主要机理。

1 实验设备及测试技术

1.1 高超声速静风洞

钝锥转捩实验在国防科技大学Ф300 mm 高超声速静风洞完成。该风洞采用上吹下吸的运行方式，喷管采用轴对称短化设计，喷管出口直径为300 mm。为了尽可能保持喷管壁面为层流边界层，在喷管喉道上游采用抽吸方式抽除稳定段收缩段发展起来的边界层。风洞运行的名义马赫数为6，正常运行时间长达30 s，可以通过调节来流总温总压改变来流雷诺数。

1.2 温敏漆测试技术

温敏漆技术是测量边界层转捩经常采用的一种方法。温敏漆在一定波长的入射光照射下，能够发射出波长与入射光显著不同的激发光，并且激发光的强度随温度升高而单调降低。在高超声速条件下，气流的摩擦加热使得层流区和湍流区之间的温度差异非常显著，利用温敏漆这一特性，将温敏漆材料涂覆在模型表面并在一定波长的入射光进行照射，利用相机拍摄激发光强的变化情况。当边界层由层流转变为湍流时，表现为图像上的局部温度陡升，通过壁面温度变化这一现象可以确定边界层转捩位置。

1.3 实验模型

实验模型为球头半径1.5 mm，半锥角7°，总长为500 mm 的圆锥。由于金属质模型良好的导热性，边界层内的热量会被金属模型吸收，从而导致温敏漆的测量结果不能准确反映出边界层的转捩特性，因此选取绝热性较好的电木材料加工为实验模型。利用温敏漆技术对典型状态下的钝锥边界层流动特性进行测量。

2 数值方法

2.1 控制方程和计算方法

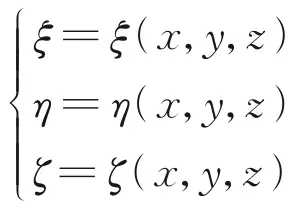
数值模拟的流动环境为来流马赫数Ma=6，来流静温T∞=52 K，来流单位雷诺数Reunit=1×107m-1，迎角α=10°。壁面温度Tw条件分别为42、84、126、168、210、252、294 和336 K，对应的壁温比分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7 和0.8。采用有限体积法求解三维可压缩Navier-Stokes 方程，无黏通量采用二阶TVD 格式进行离散，限制器采用基于Minmod 函数的对称限制器，黏性通量采用二阶中心差分格式进行离散，时间推进采用LGS 隐式方法。计算域包含由钝头产生的激波，流向和法向均采用变网格，流向网格最小间距小于0.1 mm，壁面法向第一层网格间距为0.001 mm。考虑到背风面中心子午线附近区域流场变化较强，周向采用变网格进行局部加密计算。

2.2 稳定性分析与转捩预示

根据线性稳定性理论，小扰动可以写成行进波形式

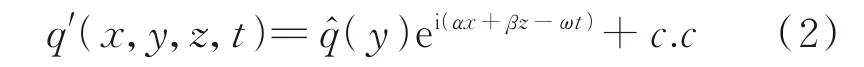
骨痛症状、分化程度、骨转移数目、骨转移部位、合并骨外转移、初诊临床分期、初诊时ECOG(东部肿瘤协作组)评分、化疗是影响胃癌骨转移的预后因素。P<0.05，具有统计学意义，见表1。

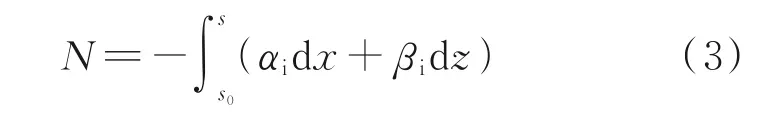
式中：s0为扰动开始增长的位置或参考位置，s为当前位置。得到N（ω，x，z）值后取所有频率下的N值包络作为预测转捩位置用的N值，即

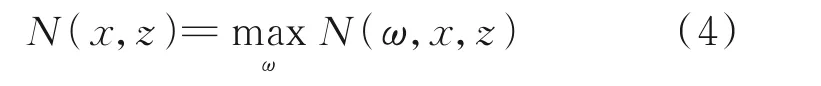
当N值达到由实验标定的某个阈值NT时，即认为流动发生了转捩。不同类型的边界层流动NT值一般需要重新标定，因此eN方法是一种半经验的转捩预测方法。

3 转捩天地差异分析

3.1 风洞实验转捩结果

图1 为圆锥迎风面在静风洞中的温敏漆测量结果。由图可以看出，圆锥迎风面上的边界层转捩阵面为“V”字形。由于相机视角的原因，所拍摄的圆锥迎风面的温敏漆图像不是完全对称的，但定性上与文献［20］中HIFiRE-1 圆锥外形的地面实验测量结果是一致的，如图2 所示。

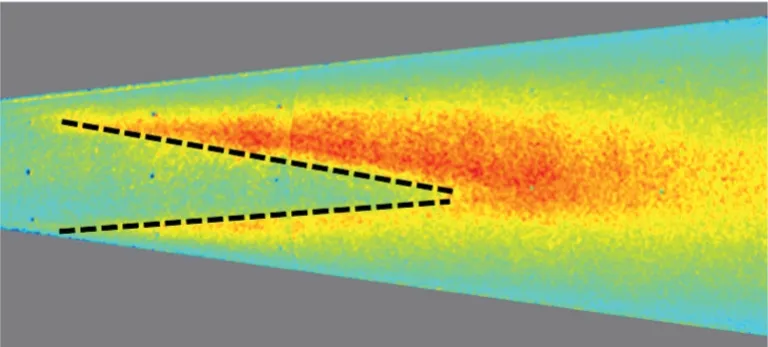
图1 来流单位雷诺数为1.0×107/m，10°迎角下钝锥迎风面的温敏漆测量Fig.1 Temperature-sensitive paint image of windward side of blunt cone at 10°angle of attack under freestream unit Reynolds number of 1.0×107/ m

图2 HIFiRE-1 钝锥外形迎风面的红外热图测量[20]Fig.2 Infrared map of windward side of HIFiRE-1 blunt cone[20]

3.2 飞行试验转捩结果

图3 为HIFiRE-1 圆锥在飞行状态与地面状态条件下不同子午线上的转捩雷诺数分布。其中，黑色实线、红色虚线及蓝色点划线为飞行试验测量结果，黑色实心三角与红色实心方块的连接线为H2K 常规风洞的地面测量结果。图中周向角φ=0°（或φ=360°）代表迎风中心子午线，φ=180°代表背风中心子午线。为了与文献保持一致，下文中的研究内容也均按照该方法对迎背风面进行定义。由于转捩雷诺数与转捩位置成正比，因此图中的转捩雷诺数分布可间接地反映出圆锥的转捩形貌。由图还可以看出，在飞行状态下，圆锥迎风中心子午线φ=0°（或φ=360°）与φ=90°子午线（或φ=270°子午线）上的边界层均先于上述子午线之间的位置转捩，圆锥迎风面（φ=270°～90°子午线）的转捩形貌基本呈“W”形。在风洞状态下，背风中心子午线φ=180°最先发生转捩，迎风中心子午线φ=0°最后发生转捩，背风面先于迎风面转捩。圆锥在飞行状态与地面状态下的转捩形貌存在显著的差异。

图3 HIFiRE-1 飞行试验与地面实验状态下钝锥转捩阵面对比[15]Fig.3 Comparison of HIFiRE-1 transition morphology in the cases of flight test and ground experiment[15]

采用基于线性稳定性理论的eN方法分别对地面状态与飞行状态下的球锥边界层进行转捩预示，如图4 所示。可以看出，无论是对于地面状态还是飞行状态，预示结果均与测量结果一致。

图4 地面实验与飞行实验状态下钝锥边界层的eN 方法对转捩形貌预示Fig.4 Transition morphology of blunt cone boundary layer under flight and ground conditions predicted by the eN method

3.3 壁温比对钝锥边界层转捩的影响

飞行试验状态和地面实验状态下的圆锥转捩特性具有显著差异。由风洞实验和飞行试验条件可以得出，风洞状态的壁温比Tw/T0一般在0.6～0.7，而飞行状态下的壁温比Tw/T0一般在0.1～0.2，下面将对不同Tw/T0对钝锥边界层转捩的影响开展分析。

3.3.1 基本流分析

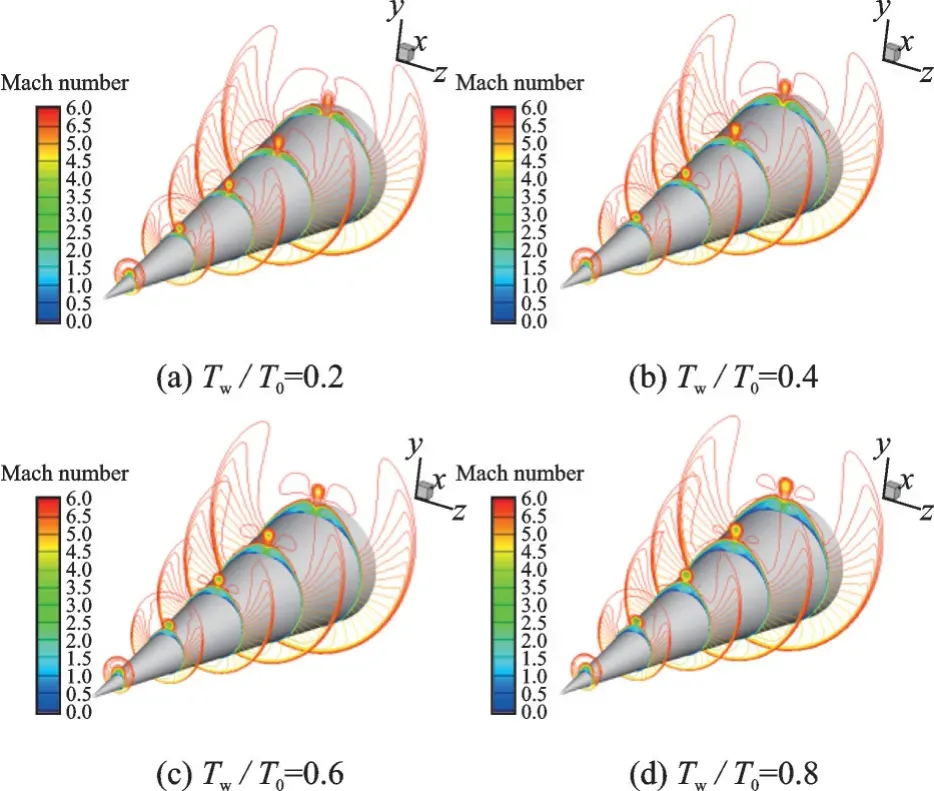
图5 不同壁温比条件下的马赫云分布Fig.5 Distributions of Mach number contours under different ratios of wall temperature to total temperature

图6 给出了圆锥在不同壁温比条件下的壁面极限流线分布。从图中可以看出，圆锥边界层内的流线明显从迎风面向背风面弯曲，呈现出明显的三维性特征，圆锥边界层在背风面出现了一次分离和二次分离的流动现象。壁温比越大，发生一次分离和二次分离的位置越趋向于背风中心线。

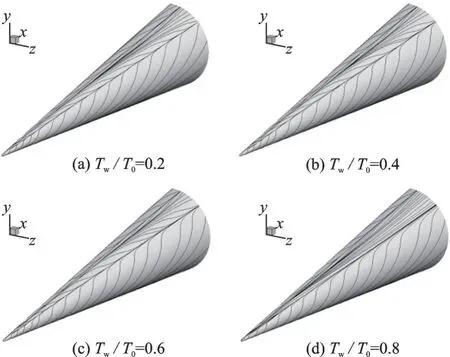
图6 不同壁温比条件下的壁面极限流线分布Fig.6 Distributions of surface limiting streamlines under different ratios of wall temperature to total temperature

图7 给出了不同壁温比条件下流向x=300 mm，周向φ=60°与120°处的势流方向速度、横流速度、温度和密度沿壁面法向分布。由图7（a，b）可以看出，随着壁温比增大，势流方向速度剖面抬升，边界层厚度增大。同时，横流速度逐渐增大，横流效应增强，最大横流速度对应的法向位置增大。由图7（c，d）可以看出，随着壁温比增大，边界层内同一壁面法向位置处的温度也相应地升高，温度边界层变厚。同时，边界层内同一壁面法向位置处的密度减小。

图7 不同壁温比条件下x=300 mm，φ=60°与120°处的特征物理量剖面Fig.7 Profiles of characteristic physical quantities at x=300 mm along the φ=60° and 120° meridians under different ratios of wall temperature to total temperature

3.3.2 稳定性与转捩特性分析

图8 为壁温比Tw/T0=0.2 时流向x=300 mm，周向φ=60°与120°处不稳定扰动的增长率分布。由图可以看出，第一模态和第二模态的中性曲线关于展向波数β呈非对称分布，第一模态出现了频率为零的横流定常涡。圆锥的横流及边界层厚度对第一模态和第二模态具有不同的影响，因此对于某个固定频率下，导致第一模态与第二模态不稳定扰动的展向范围也不同。

图8 壁温比Tw/T0=0.2 时流向x=300 mm，周向φ=60°与120°处不稳定扰动增长率分布Fig.8 Growth rate distributions of unstable waves at x=300 mm along φ=60° and 120° meridians under Tw/T0=0.2

图9 为不同壁温比条件下流向x=300 mm，周向φ=60°与120°处第一模态与第二模态中性曲线分布。由图可以看出，随着壁温的增大，第二模态不稳定波的失稳频率范围减小，相应地，第一模态不稳定波的失稳频率范围增大。因此，壁温比的增大，抑制了第二模态波的发展，促进了第一模态波的发展。

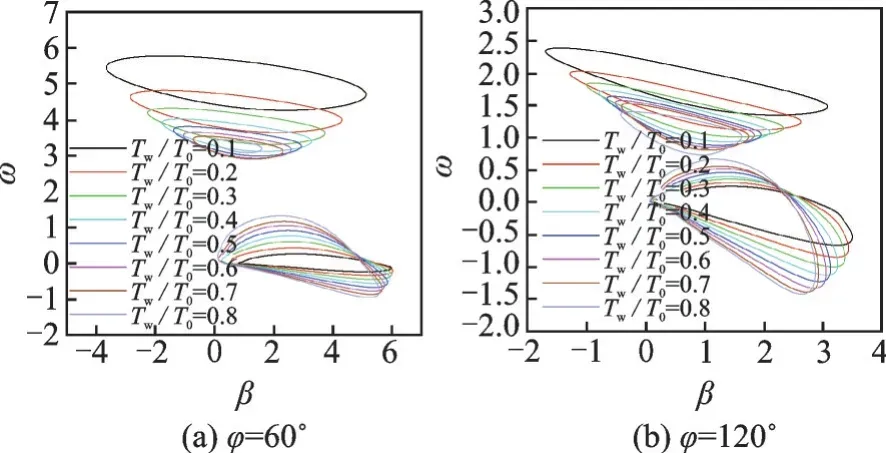
图9 不同壁温比条件下流向x=300 mm，周向φ=60°与120°处第一模态与第二模态中性曲线分布Fig.9 Neutral curves of the first and the second modes at x=300 mm along φ=60° and 120° meridians under different ratios of wall temperature to total temperature

图10 为采用eN方法得到的不同壁温比条件下的圆锥N值包络分布。由图可以看出，壁温比不同，圆锥表面的N值包络分布也不同，壁温比对N值分布具有显著影响。由图还可以看出，低壁温比时，圆锥迎风中心与侧面的边界层先于两者之间位置转捩，转捩形貌与飞行试验结果相似；高壁温比时，圆锥迎风面区域迟于侧面及背风面区域转捩，转捩形貌与风洞实验结果相似。

图10 不同壁温比条件下的N 值包络分布Fig.10 N-value envelopes under different ratios of wall temperature to total temperature

图11 为不同壁温比条件下N=3 时不同频率扰动引起的转捩线位置。由图可以看出，由横流驻波引起的转捩区占据了圆锥表面大部分区域。在圆锥边界层内还存在多种频率成分的流向不稳定扰动波，且随着流向扰动波频率的增大，其引起的边界层转捩有向迎风面移动的趋势。通过对比流向扰动波和横流驻波的转捩线位置可以得出，横流不稳定性在大部分流动区域占主导作用。随着壁温比的增大，由横流驻波引起的转捩线同时向迎、背风面移动，转捩区前移并增大；边界层内较低频率的流向不稳定波消失，流向不稳定扰动的频带变窄并向迎风面移动，此时边界层在背风面的转捩主要由横流不稳定波引起，在迎风面的转捩则主要由高频不稳定波引起。随着壁温比继续增加，高频不稳定波消失，低频不稳定扰动开始出现并增强。由于低壁温比条件下，高频第二模态波得到促进，因此圆锥迎风中心线附近区域先发生转捩。随着壁温比增大，高频第二模态波得到抑制，迎风中心线附近区域后发生转捩。

图11 不同壁温比条件下N=3 时不同频率扰动引起的转捩线位置Fig.11 Transition positions induced by various frequency disturbances when N=3 under different ratios of wall temperature to total temperature

4 结 论

本文首先对比了天上飞行状态与地面风洞状态下钝锥边界层的转捩特性，然后利用基于线性稳定性理论的eN方法分别对飞行试验状态与风洞实验状态下的钝锥边界层进行了转捩预示，最后研究了壁温比对钝锥边界层的稳定性及转捩特性的影响，揭示了壁温比是造成钝锥边界层转捩天地差异的主要影响因素。主要结论如下：

（1）在飞行试验状态下，圆锥0°子午线和90°子午线上的边界层均先于上述两子午线之间区域转捩，圆锥迎风面的转捩形貌呈“W”形。在风洞实验状态下，圆锥迎风面迟于背风面转捩，迎风面上的边界层转捩形貌呈“V”形。

（2）在低壁温比条件下，圆锥迎风中心与侧面的边界层先于两者之间区域转捩，转捩形貌与飞行试验结果相似。在高壁温比条件下，圆锥迎风面区域迟于侧面及背风面区域转捩，转捩形貌与风洞实验结果相似。