Heisenberg群上两类带权对数型Hardy-Sobolev不等式
2022-08-30张君丽
张君丽
(西北工业大学 数学与统计学院,西安 710129)
Hardy-Sobolev不等式可应用于分析学的许多邻域,如泛函分析,调和分析,概率论和偏微分方程等。在偏微分方程中,这些不等式常常被用来研究解的先验估计,存在性,正则性以及渐近性等[1-8]。此外,具最佳常数的Hardy-Sobolev不等式也可用于研究一些非线性特征值问题[9]。对于Hardy-Sobolev不等式,有许多学者通过不同的方法在不同的函数空间上进行了研究。文献[10]在H-型群上通过Hardy不等式得到了Hardy-Sobolev不等式,Hardy不等式的研究还可参见文献[11-16],在H-型群上的研究还可参见文献[17]。文献[18]在各项异性Heisenberg群上同样通过Hardy型不等式得到了Hardy-Sobolev不等式。文献[19]在Carnot群上通过Lp(1 注意到,文献[10,17-19,21]中的Hardy-Sobolev不等式都是由Hardy(型)不等式推出的,而文献[20]中的Hardy-Sobolev不等式则由Poincaré不等式推得。文献[22-23]分别是在Baouendi-Grushin向量场和Herz-Morrey空间建立的Hardy-Sobolev不等式。文献[24-26]均是在欧氏空间上建立的不等式,且文献[25-26]中的不等式涉及了对数。从这些参考文献中,可以观察到研究Hardy-Sobolev不等式的难点在于找到合适的切入口,如Hardy(型)不等式和Poincaré不等式等。 文中从Heisenberg群上由次椭圆A- Laplace不等方程导出的Hardy型不等式出发,得到Heisenberg群上两类带权对数型Hardy-Sobolev不等式。考虑次椭圆A- Laplace不等方程 -ΔH,Au≥f(ξ),ξ∈Ω, (1) A(s)=B(|s|)s,s∈2n, (2) 这里B为径向函数;并记 (3) 即可,其中非负函数ω满足相容性条件(见下文的假设(H1)和(H1)0)。 (4) (5) (6) 关于N-函数的定义和性质可参见文献[27]。 文中所需假设如下: (H1) 存在一个非负的C1((0,∞))函数Ξ:[0,∞)→[0,∞),满足如下条件: (i)存在某个连续函数ω:(0,∞)→(0,∞),使得不等式 ω(t)Ξ′(t)≤-cΞ(t),t>0 (7) 成立,其中c>0(与t无关),且Ξ(t)/ω(t)是非增的; (ii)函数 s (8) 在0的邻域内非增或有界; (H1)0存在一个非负的属于C1(u(Ω){0})的函数Ξ,其中u(Ω)={u(ξ):ξ∈Ω},满足如下条件: (i) 对所有的t∈u(Ω) (ii)由式(8)给定的函数H(t)在0的邻域非增或有界。 (H2) 存在δ∈,使得下式成立 (9) 定义 δ0:=inf{δ∈:f+ (10) 对假设条件(H1)和(H1)0,文中给出下列两个注。 注1假设(H1)(i)蕴含了Ξ在(0,∞)上是递减的,这从式(7)看出。此外,为确保Ξ(t)/ω(t)是非增的,只需ω′(t)≥-c即可,其中c如式(7)中所示。 注2 可以看到假设(H1)0比(H1)弱,举例如下:取 (11) 则u(Ω)⊆(0,σβ)。容易看到Ξ在(1,∞)上不是一个减函数,从注1知Ξ不满足(H1)(i)中的条件,但满足条件(H1)0(i)中的条件。 文中主要结果包括Heisenberg群中如下两类带权对数型Hardy-Sobolev不等式: (12) 其中 |ξ|β-2|z|)dξ, 这里ξ=(x,y,t),z=(x,y), (13) 其中 |ξ|p(β-2)-β|z|plnα(2+β|ξ|β-2|z|)dξ, lnα(2+|ξ|β|βln|ξ||-1)dξ, Heisenberg群Hn是指在2n+1上赋予群运算所得的群,其中ξ=(z,t)=(x,y,t)=(x1,x2,…,xn,y1,y2,…yn,t);z=(x,y),x∈n,y∈n,t∈,n≥1;ξ′=(x′,y′,t′)∈2n+1。Heisenberg群上的齐次维数为Q=2n+2,左不变向量场为 i=1,2,…,n。 记Hn上的水平梯度为 ∇H=(X1,X2,…,Xn,Y1,Y2,…,Yn), 散度为 次Laplace ΔH为 对任意的ξ,ξ′∈Hn,Hn上的距离函数定义为 d(ξ,ξ′)={[(x-x′)2+(y-y′)2]2+ [t-t′-2(xy′-x′y)]2}1/4。 若ξ′=0,则 d(ξ)=d(ξ,0)={|z|4+t2}1/4, 其中 |z|=(x2+y2)1/2, (14) 通常称d(ξ)为齐次范数。 对d=d(ξ)>0,容易计算出 (15) (16) (17) 关于Heisenberg群的更多细节见文献[28]。 在Luxemburg范数 下是一个Banach空间。 类似于文献[1]中定理4.1(欧氏空间上的Hardy型不等式)的证明,可得如下Heisenberg群上的结论: (18) 则对每一个在Ω中有紧支集的Lipschitz函数ζ,成立 (19) 其中 (20) (21) (22) 为证明定理1,需要以下两个引理。 (23) 其中 μ1(dξ)= (24) μ2(dξ)=ωp-1(u)lnα(2+ω(u))Ξ(u)χ{|∇Hu|≠0}dξ, (25) (26) 证明利用引理1.1来证明。设0 所以 (27) 因为 所以式(6)中的 (28) (29) 再注意到 因此,直接应用引理1.1,即得式(22)。 在引理2.1的基础上,取式(1)中的 |z|p|ξ|(β-2)(p-1)-2lnα(2+β|ξ|β-2|z|), 0<β<1, 则可以证明u=|ξ|β是式(1)的一个非负弱解,进而有下列结论。 假设(H1)满足,其中 (30) 则存在常数C>0使得对每一个在Ω中有紧支集的Lipschitz函数ζ有 (31) 其中 μ1(dξ)= (32) μ2(dξ)=Ξ(|ξ|β)ωp-1(|ξ|β)lnα(2+ ω(|ξ|β))dξ, (33) C见式(26)。 证明为了用引理2.1,文中来检验假设(H0)和(H2)满足。假设(H0)显然满足,下面验证假设(H2)。先证u=uβ(ξ)=|ξ|β是式(1)的一个非负弱解。注意到当t>0时, 令u=uβ(ξ)=|ξ|β,其中β>0。由式(16)和式(17)知 所以 ∇Hu=β|ξ|β-1∇H|ξ|, |∇Hu|=β|ξ|β-2|z|, ΔHu=divH(β|ξ|β-1∇H|ξ|) =β(β-1)|ξ|β-2|∇H|ξ||2+ β|ξ|β-1ΔH|ξ| =β(β-1)|ξ|β-4|z|2+ =β(2n+β)|ξ|β-4|z|2。 从而 =|∇Hu|P-2lnα(2+|∇Hu|)ΔHu -|∇Hu|P-2lnα(2+|∇Hu|) ≥|∇Hu|P-2lnα(2+|∇Hu|)ΔHu· |z|plnα(2+β|ξ|β-2|z|)=f。 因此,u=uβ(ξ)=|ξ|β是式(1)的一个非负弱解。 |z|plnα(2+β|ξ|β-2|z|)ω(u) + δβp|ξ|p(β-2)|z|plnα(2+β|ξ|β-2|z|) =βp|ξ|p(β-2)|z|plnα(2+β|ξ|β-2|z|)· 因此假设(H2)满足。 现在引理2.1的条件满足,于是应用引理2.1得引理2.2成立。 定理1的证明令引理2.2中的Ξ(t)=t-c,c>0,ω(t)=t。显然Ξ和ω在(0,∞)上都是正函数,Ξ∈C1(0,∞),Ξω-1递减,且 Ξ′(t)ω(t)=-ct-c=-cΞ(t)。 且当p-1-c≥0时,H(t)在0的邻域内是有界的;当p-1-c<0时,H(t)在0的邻域内递减。因此假设(H1)成立。因为 所以引理2.2的条件满足,因此应用引理2.2得定理1成立。 注4将假设条件(H1)换成更弱的(H1)0,仍有相应的引理1.1,引理2.1和引理2.2成立,证明是类似的,不再叙述。 从而取(H1)01) 中的c=1。 进一步 容易计算出对充分小的t>0有 =ωp-1(t)lnα(2+ω(t))· 因为对u=|ξ|β,有 所以存在δ∈[δ0,c)=[δ0,1)。从而满足假设(H1)0的引理2.2的条件满足,因此应用引理2.2得定理2成立。 1) 文中从Heisenberg群上次椭圆A-Laplace不等方程-ΔH,Au≥f(ξ),ξ∈Ω出发,推导Heisenberg群上两类带权对数型Hardy-Sobolev不等式。 2) 在假设条件(H0),(H1)和(H2)下,利用A-Laplace不等方程导出一个Hardy型不等式,通过取满足假设(H0),(H1)和(H2)的函数,进行一系列的计算和估计便得第一类带权对数型Hardy-Sobolev不等式,即定理1。 3) 将假设条件(H1)换成更弱的(H1)0,同样可得Hardy型不等式成立,通过取满足假设(H0),(H1)0和(H2)的函数,进行一系列的计算和估计便得第二类带权对数型Hardy-Sobolev不等式,即定理2。

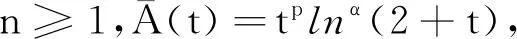






1 预备知识



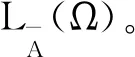





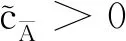
2 主要结果的证明










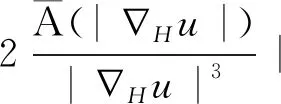
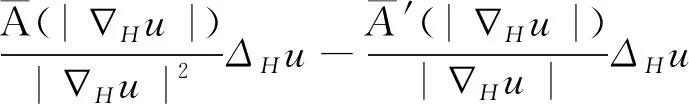





3 结 论
