改进型加权实时融合算法在提高遥测数据质量中的应用
2022-08-30唐艺灵
唐艺灵
(中国人民解放军92941部队,辽宁 葫芦岛 125001)
0 引言
在指挥控制系统中,遥测数据实时处理是态势感知的重要环节,其任务是将来自各测量设备的实时遥测数据按照一定规范进行解析,最终将能反应飞行器工作性能的参数及飞行器航迹显示在指控大厅,供指挥决策及故障诊断。因此,遥测数据处理结果必须实时、准确,遥测处理结果质量好坏直接影响任务的圆满完成。在实时数据处理中,通常用以下两种方法来提高遥测数据的质量:一种是从测量设备入手,即使用接收能力更强的地面遥测设备,或增加设备数量并优化设备布站等;二是优化数据处理方法,包括建立更加准确的设备误差模型,研究更加有效的实时数据融合方法,采用先进的数据定位及选优策略等[1]。实际任务中遥测数据一般由多个设备同时进行测量,数据源选取是按照时域或空域对各设备测量数据进行拼接,最终形成一个完整数据流。然而在实际任务中,有时设备获得的数据质量很高,但在参数及航迹计算时,却因为选择了部分不好的设备测量数据参与处理从而导致参数及目标航迹出现跳变,致使信息失真,有时则因为设备、环境或目标的原因导致测量信息不充分[2-3]。如何通过综合获取的所有有效测量元素,实现数据的高精度平滑输出,成为信息处理中需要持续研究的课题。
国内外已有很多文献,基于实际应用提出了一些处理方法。文献[4]提出一种基于一阶差分的野值类型判别及处理方法,能够准确判断野值类型及位置。文献[5]针对处理过程中出现的有效定位数据过度滤除以及无效数据滤除不干净的问题,基于DS证据理论的有效性实时判别方法,利用遥测数据中的定位数据信息和理论信息,预测数据合理范围,直接判断数据有效性,有效滤除数据中的无效数据。文献[6]研究了国内外多传感器数据融合技术现状,并提出三种实时抗野值的修正方法:简单经纬度法、最小二乘法和抗野值Kalman滤波方法。但这些算法或需要根据不同的设备设置不同的参数,计算较繁琐,或当野值数量较多时,外推数据过长往往影响了数据的精确性,或出现断点。文献[7]针对简单剔野方法无法剔除连续野值以及样条拟合方法复杂的参数估计问题,分析不同运动模型下的目标差分特性,提出了分段剔野方法,通过分别建立模型,使得算法更加简单,拟合数据更能反映目标真实运动,从而使得野值修正更加准确。文献[8]在测量设备与被试品相等精度的情况下,提出可以通过增加测量次数来弥补测量误差带来的不利影响,确保两者的估值精度维持在相同水平上。但这些方法都是建立在事后数据处理基础上,不适合实时的情况。
对于跨区域联合试验新模式,数据处理具有两个新特点:1) 数据来源于两个区域不同测量体系,各区域测量设备精度、设备布站方式及解算数据方法存在差异;2) 由于测量距离的增加,遥测数据更易受到通讯、方位、距离、电磁环境等干扰信号影响,更易出现野值。
因此,为了圆满完成跨区域遥测实时处理任务,使数据处理结果完美展示在决策者面前,有必要研究更优的跨区域遥测实时处理方法。本文提出一种提高遥测数据质量的改进加权实时融合算法。
1 遥测数据融合算法原理
1.1 问题分析
假设某任务区域内部署了m个测量设备,采用接力式对飞行器进行测量,如图1所示。
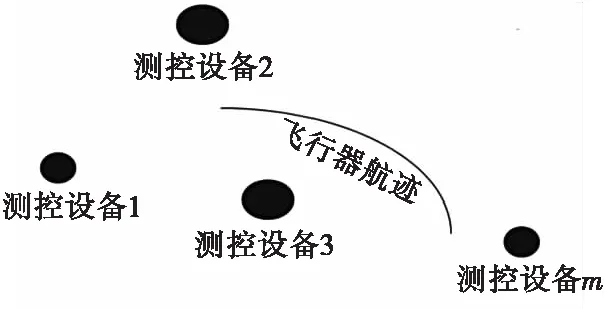
图1 测量示意图Fig.1 Measurement schematic diagram
在任务开始之前,将飞行器航迹分为n个测量段,保证每个测量段都有至少一个测量设备做为数据源。根据飞行器的理论轨迹,并综合考虑设备精度、布站位置等因素可以计算测量设备的有效时间段落。经过分析,跨区域任务测量段落可分为三个部分,即区域1、区域1和区域2重叠部分、区域2,如图2所示。
区域1为只有区域1的设备能测量到的区域范围,区域2为只有区域2的设备能测量到的区域范围,区域1和区域2重叠部分为两个区域的测量设备都能测到的范围。因此,区域1、区域2测量方式和不跨区域任务时相同,重点是区域1和区域2重叠部分的测量,重叠部分靠近区域边界,都不是两个区域测量设备最优测量段落,极易因通信误码、测量方位等原因产生野值。目前,野值数据的判别和剔除已经有很多成熟的处理方法。为了获得高精度、准确、平滑的信息处理,对于区域1和区域2重叠部分可以考虑充分发挥多信息源优势,采取数据融合处理方法,而区域1、区域2进行融合处理意义不大,通过对以往任务数据的事后分析也可说明这一点。区域1、区域2的数据首先是来自同一测量体系,数据处理方法一致,测量段落都已经划分得很细,确保处于最佳威力范围内,各设备接收信号情况也基本一致,因此可认为数据是等精度的。通过上述分析数据处理结果选优示意图如图3所示。
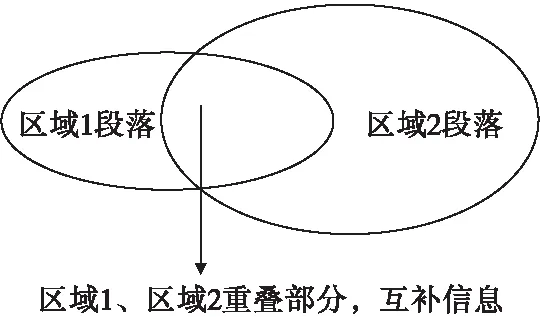
图2 任务段落示意图Fig.2 Task section schematic diagram
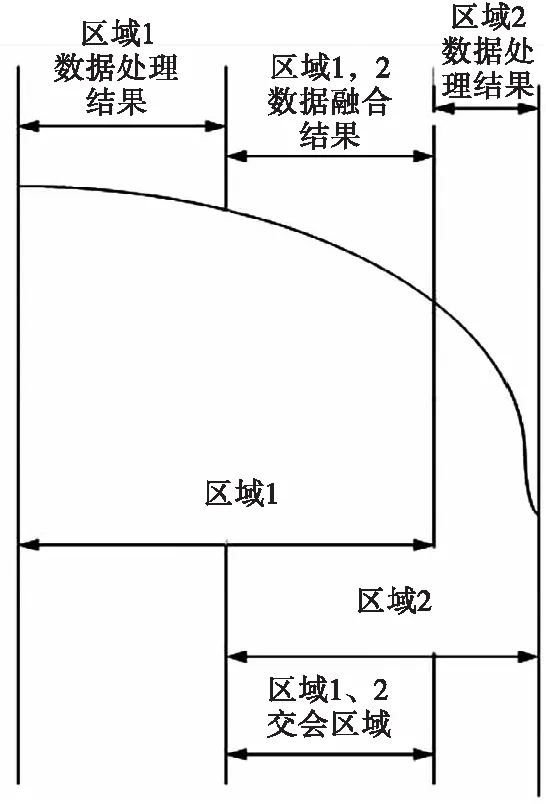
图3 数据处理结果选优示意图Fig.3 Data processing result prepotency schematic diagram
1.2 数据实时融合算法
目前多传感器数据融合尚未形成完整的理论体系,但在很多文献中,已经根据各自具体的应用需求,提出了一些有效的融合方法[9-10]。相对于神经网络、贝叶斯决策等融合技术需要大量数据集进行建模,存在局限性[11-12],加权融合处理因为融合方法简单实用而且精度高,在强实时应用场景中备受关注。
文献[13]将证据理论中的修正证据距离引入传感器测量数据间相互关系的计算,依靠传感器间测量数据的相互关系确定融合权重,仿真结果验证了算法融合效果好,但不符合加权融合最优分配的原则。文献[14]研究了飞行测量数据实时融合检择关键技术,提出两信息源、多信息源航迹融合检择技术,通过剔除融合前原始信息的野值,有效解决了因过失误差而造成的融合结果精度偏低问题,但算法较为繁琐。文献[15]提出一种多站遥测数据加权融合处理方法,构建了融合权重与测量精度之间的对应计算模型及测量设备实时测量精度模型,通过典型算例进行验证,并与固定标称值测量精度最小二乘加权融合算法及利用传感器间测量数据相互关系确定权重的加权融合算法进行对比分析,所提算法融合效果优于上述两种方法,具有较好的应用价值,但算法是依据设备的实测数据的统计分析计算测量精度,实时性还有待验证。
结合任务实际情况,在借鉴传统分批估计算法的基础上,提出改进型分批估计与分组动态加权实时融合算法。该方法对测量设备先进行分组再分批估计,并引入异常因子作为去除临界值的最优百分比,最后针对误差分布不均特点,实时计算测量精度,进而求出动态权值,实现自适应加权融合,方法简单,易于编程实现。
2 改进型分批估计与分组动态加权实时融合算法
2.1 改进型分批估计与分组动态加权融合算法
假设测量数据来自s个数据源:U(t)1,U(t)2,…,U(t)s,测量数据融合的过程模型如图4所示。
1) 实际测控中,存在着误差偏大甚至错误的测量数据,这类数据称为粗大误差,必须及时剔除,否则影响整体的测量结果,因此首先对数据进行预处理,剔除含粗大误差的数据项,得到具有一致性的有效数据序列U′(t)。
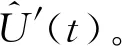
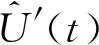
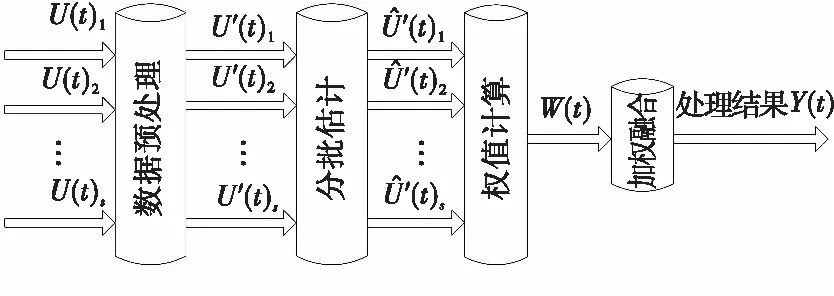
图4 数据融合的过程模型Fig.4 Process model of data fusion
在实际测量过程中,受到复杂因素影响,可能存在均方差偏大的一致性测量数据,传统分批估计算法没有考虑对这类数据进行特殊处理,只进行简单算术均值计算,这类数据往往会引起最终计算结果的误差偏大。因此引入异常因子对传统分批估计算法进行改进,异常因子是指去除最大最小值的最优比率。依据统计理论和实践经验,剔除部分最大最小值后获取的均值数据,具有更高的精度和稳定性,也更能反映数据的集中情况。
由于单一测量设备在某时刻只有单一测量值,不能直接采用分批估计算法对数据进行计算,因此采取分组的方式进行分批状态估计。按照一定的规则将来自不同数据源的数据分为v组。以第一组测量数据为例,设测量数据为:U(t)11,U(t)12,…,U(t)1m,实时计算算术平均值为:
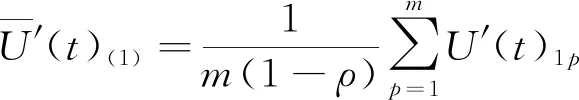
(1)
式(1)中,ρ为异常因子,是指去除最大最小数量的最优比率。p∉P且P为一个集合,即P={下标为ρ与P的积的值}。
标准差为:
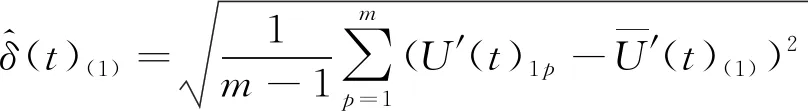
(2)
根据式(1)、式(2)计算出其余各组的算术平均值和标准差,得到算术平均值序列和标准差序列:
及
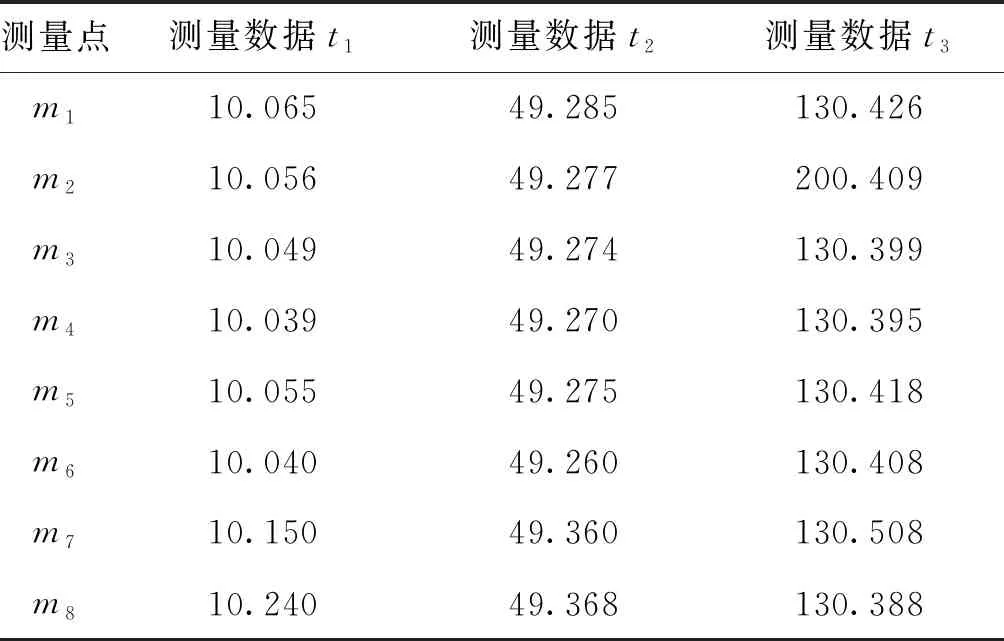
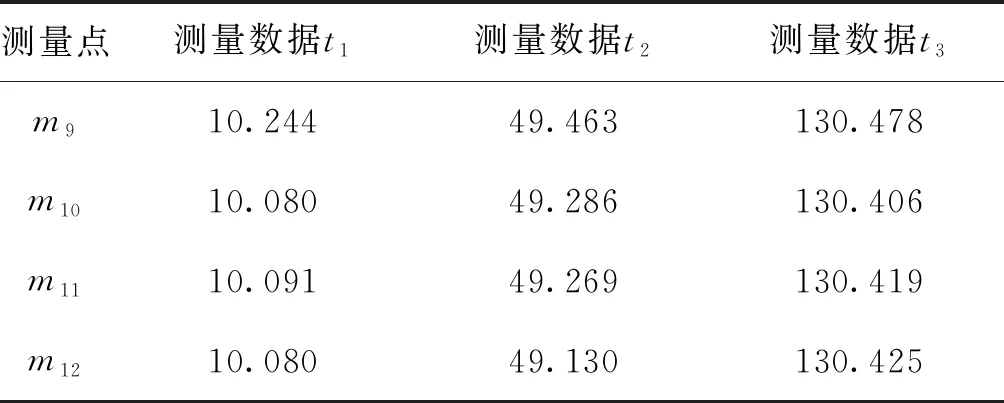
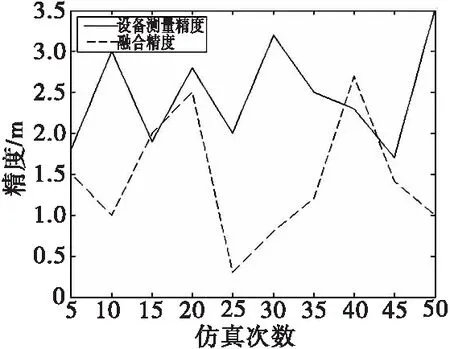
因此,通过分组使s个数据源的数据融合问题转化成对含有v组数据的数组序列融合的问题(s 在区域内通常有多个测量设备,每个设备因方位、使用等因素,测量值存在差异,测量误差分布不均匀,具有很大随机性。对此,需要解决的问题是,如何有效对待各个数据源的数据差异,来提高数据融合结果的质量。在实际任务中采用了实时计算数据源测量精度,进而根据方差实时计算权值,再采用权值最优分配原则实现动态加权融合的方法。该方法在方差大时给予数据较小的权值,方差小时给予数据较大的权值,从而实现为每个测量数据自适应探求其最优权值,以获取其最小总误差,从而得到被测目标的最优估计值。当遇到突发异常时,自适应加权数据融合结果将更具有准确性和稳定性。 各组数据的加权因子由式(3)求得。 (3) 采用自适应加权融合算法对这v组数据进行处理,获得更接近真值的融合估计值Y(t)。该组数据的融合估计值由式(4)求得。 (4) 数据预处理,分批估计需计算的均值、方差均为单层循环,时间复杂度为O(m);权值计算为单层循环,时间复杂度为O(v);如m>v,该算法的时间复杂度为O(m);如m 通过仿真的模拟数据验证本文所提改进后处理算法的有效性。取某遥测参数M,数据源为外部区域m1,本地遥测设备m2~m12,设不同数据源某时刻的测量数据分别为t1,t2,t3,并设置一定比例的异常值。各数据源数据如表1所示。 表1 各数据源测量数据Tab.1 Measurement data of each data source 续表 分别计算融合算法改进前和改进后的估计值。测量数据t3是需去除m2设备粗大误差200.409。 分组数根据数据源的数量设定,数据源较多时,分组数就越多,方差越小,优点更明显。依据位置就近原则,将m1~m4分为第一组,m5~m8分为第二组,m9~m12分为第三组,同时根据实际情况设定ρ的取值。当ρ达到一定值时,融合估计值变化逐渐趋于平稳,这里取ρ=0.05。t1时刻算法改进前及改进后测量数据处理结果如表2所示。t2时刻算法改进前及改进后测量数据处理结果如表3所示。t3时刻算法改进前及改进后测量数据处理结果如表4所示。 表2 t1时刻测量数据处理结果Tab.2 The processing result of measure data at t1 表3 t2时刻测量数据处理结果Tab.3 The processing result of measure data at t2 表4 t3时刻测量数据处理结果Tab.4 The processing result of measure data at t3 由以上数据处理结果可见,采用改进型分批估计方法得到的方差更小,其结果更接近真实值。改进后各个时刻的融合值如表5所示。 进行50次仿真,将设备精度与融合精度进行对比,对比结果见图5所示。从图5可以看出上述方法融合精度明显高于设备原始数据精度。经对实测数据统计分析,测量数据处理时延符合技术指标规定允许最大时延,采用融合算法时延仅比未采用融合算法大0.06 ms,满足绝大部分强实时应用场景。 表5 各时刻测控数据融合值Tab.5 Fusion value of measurement and control data at each time 图5 设备精度与融合精度对比Fig.5 Comparison of equipment accuracy and fusion accuracy 本文提出局部区域数据融合进行状态估计的方法,采用先分组再分批估计的方式并引入异常因子,实现分组动态加权融合,应用于跨区域多信源实时遥测数据处理中,有效降低了由于距离增加产生的环境干扰、失效数据及数据源精度差异所带来的影响,获得了具有较高精度和稳定性的结果数据。如果应用于测控距离较短的任务中,由于实测中数据源稳定且误差较小,数据融合相对单一数据源优越性也较小。随着测控设备性能和测控手段的不断丰富和提高,计算机及网络技术的飞速发展给实时数据处理提供了技术支持,越来越多地要求进行跨区域、虚实结合、资源共用的联合演训,不同体制测量系统的数据融合必将成为主流,各种新方法和新系统的研究与开发成为必然。针对某些飞行器的遥测数据特性,若将部分具有较高精度的事后遥测数据处理模型和算法改进后应用到实时遥测数据处理中,也将成为实时遥测数据处理的重要发展方向。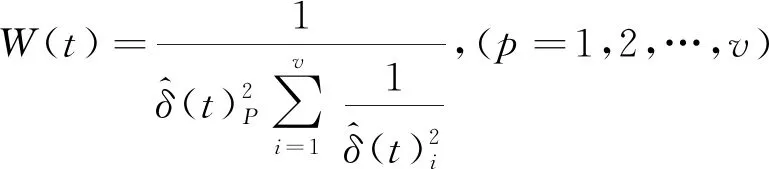
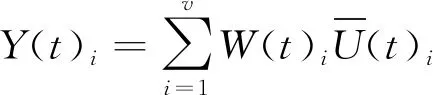
2.2 算法复杂度分析
3 实测验证




4 结论
