海底水平管线悬空机制与动力调整方法研究现状

于西达, 丛晓红, 高 枫, 拾 兵

(中国海洋大学 工程学院，青岛 266100)

引 言

21世纪以来，随着技术的发展，我国对石油资源的开采已延伸到深海地区，海底管线作为油气传输的主要途径之一，被誉为“海上生命线”[1]。在复杂的海洋环境中，由于波流、海底管线和海床泥沙的综合作用造成了海底管线悬空。悬跨段的海底管线由于受到各种应力和尾流旋涡的影响容易发生共振，从而导致海底管线失稳进而发生破坏[2]。

自第一条海底管道投入运营以来，世界各国因管道破坏而造成的事故已达数百起[3]，海底管道破坏后不仅会对海洋环境造成污染，还要耗费大量的人力物力和财力，因此海底管道的安全问题受到各国的重视。管线冲刷问题的研究起步于20世纪60年代，Herbich等[4]对管线的冲刷稳定性问题进行了研究。20世纪80年代，Kjeldsen[5]，Herbich[6]，Mao[7]，Sumer[8]等许多专家学者就已经开始通过物模试验研究了海底管道冲刷的原因与机理。进入20世纪90年代以来，仅中国海洋石油总公司开发区域就发生了数十起不同程度的海底管道破坏事故，经分析表明管道失事的主要原因是海床运动和波流冲刷后造成的管线悬空。因此开展对海底水平管线悬空机制的研究、探讨管线悬空的防护技术就显得尤为重要。本文对近年来海底水平管线的悬空机制和动力调整方法的成果进行了综述，包括悬空机理、冲刷计算、涡激振动、动力响应以及动力调整方法等；总结了现有研究存在的不足，阐明其发展趋势。

1 海底水平管线悬空机制

海底管线处在一个复杂的动力环境中，对其悬空机理的研究也十分复杂，当外界条件不同时，它会表现出不同的冲刷机理[9]。

1.1 海流作用造成的管线悬空

在复杂的海洋环境中，海流与海床之间存在着相对运动，当海流速度大于海床上泥沙起动流速时，海床上的泥沙颗粒就会发生移动，从一个位置移动到另一个位置，而初始位置的泥沙得不到补给，导致管线下方出现凹坑，从而造成管线悬空(如图1所示)。

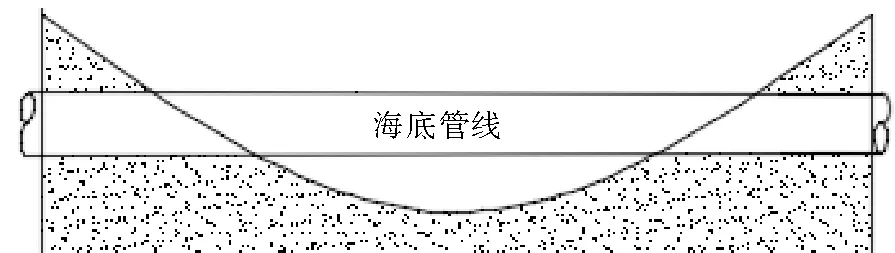
图1 海流作用造成的管线悬空Fig.1 Suspended pipeline caused by ocean current

1.2 管道应力造成的管线悬空

在管道铺设过程中存在的残余应力、温度变化产生的热应力、管道在运行过程中产生的应力集中等因素都可能使管道局部发生“屈曲”，从而造成管线的局部悬空(如图2所示)。除此之外，管线悬空段的形成还与管道的重量、强度以及管道轴向压力等因素有关。

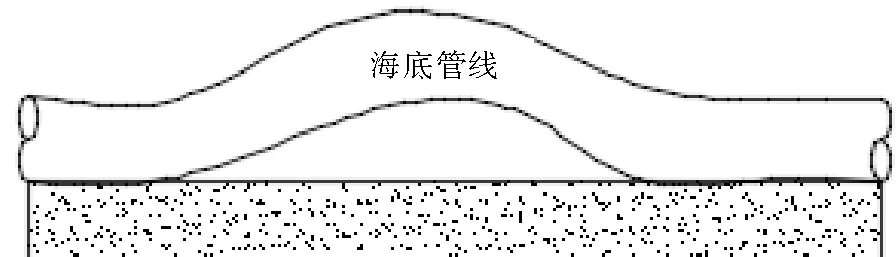
图2 管道应力造成的管线悬空

1.3 海床地形造成的管线悬空

在管道铺设时海床表面的形状、颗粒类型以及自身的重量等因素都会影响海底管线的悬跨形式和长度。如断层、礁石、错层等海床形式(如图3，图4所示)。

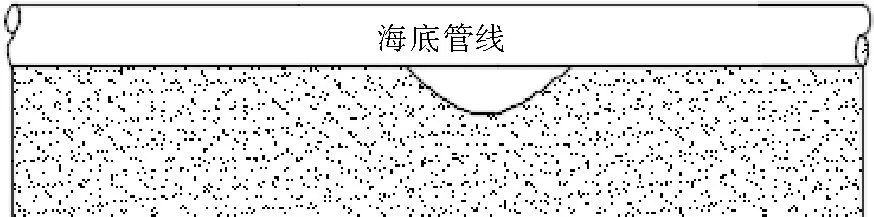
图3 海床凹凸不平造成的管线悬空

图4 海床错层造成的管线悬空Fig.4 Suspended pipeline caused by seabed split

经过分析可以看出，海底管线悬空不仅出现在运行过程中，在铺设和安装过程中也会出现不同程度的悬空。在复杂的海洋环境中，由于波流以及海洋地质条件的影响，管线悬空段容易遭到破坏，因此，对海底管线悬空问题的研究显得尤为重要。

2 海底水平管线冲刷悬空计算经验公式

海底管线的冲刷及悬空与许多因素有关，如泥沙粒径、水流条件、管线直径以及水深等，利用这些因素，很多专家学者都提出了泥沙起动以及冲刷深度的计算公式。

2.1 泥沙起动计算公式

Sumer等(2001)[10]通过对管线冲刷细节的研究，分析得出了泥沙冲刷起动的判别标准及半经验公式，如公式(1)所示:

(1)

式中,g为重力加速度；D为管径；n为泥沙的孔隙率；s为泥沙和水的相对比重；e为管线的埋深深度；u为管线上游的行近流速。

窦国仁等(2001)[11]通过分析波浪作用下泥沙颗粒受到的力，得到了2～10 m水深时波浪作用下泥沙的起动公式，并通过验证得出该公式适用于100 m以内深水中泥沙的起动，为解决河口海岸泥沙问题提供了依据，如公式(2)所示:

(2)

式中：a是与起动状态有关的参数；b是常系数；Hc是颗粒起动时的临界波高；L是波长；h是水深；T是波浪周期；ρs和ρ分别是泥沙和水的密度；d是泥沙粒径；δ和ε0分别是泥沙颗粒薄膜水厚度和颗粒间的粘结力系数；βw=(d/d1)3/4；β是反应泥沙密实程度的参数。

韩艳等(2010)[12]通过对海流和波浪作用下管线后方最易起动的泥沙颗粒受力分析，推导了床面泥沙的临界起动流速公式、冲止流速公式，分别如式(3)、(4)所示。

(3)

(4)

式中：S为泥沙与水的相对密度；λ为管线轴心处与床面接触点间平均压力梯度比例系数；λA为管线后方点压力梯度与平均压力梯度的比例系数，λA的经验公式由Zhang等(2009)[13]数值模拟方法改进后得到：λA=3.0(-15.4Fr+4.16)exp(-0.42α)；m为管线分离点前后压力分布比例系数；Fr为弗劳德数；d为泥沙的平均粒径；φ为冲刷坑泥沙休止角；CL为升力系数；CD为拖曳力系数；μ0为管线轴心高度对应的远处来流流速；μb为床面底流速。

张芝永等(2015)[14]利用波浪作用下海底管线周围水动力场-渗流场耦合数值模型研究了管线两端压差系数随KC数的变化规律，同时通过拟合分析得出了波浪作用下临界流速计算公式，如公式(5)所示。

(5)

2.2 冲刷深度计算经验公式

窦国仁(1960)[15]通过考虑水对床面颗粒的下压力和分子粘性力，推导出了粘性均匀沙的起动流速公式，如公式(6)所示。

(6)

唐存本(1963)[16]通过考虑床面颗粒的重力与颗粒之间的粘着力，推导出了粗砂和细砂的统一起动公式，如公式(7)所示。

(7)

韩艳(2010)[12]通过理论分析得出了在波浪和海流作用下稳定冲刷坑深度和管线与床面之间存在初始间隙时的冲刷坑深度公式，分别如式(8)、(9)所示。

(8)

(9)

式中,各项参数意义同公式(3)。

常留红(2014)[17]采用量纲分析方法，明确了管线局部冲刷平衡深度影响因素，建立了更为全面的水流及波浪作用下冲刷平衡深度经验公式，如公式(10)所示。

(10)

式中,S0为冲刷平衡深度；e/D为间隙比；θ为希尔兹数；α为管线参数有水流作用角。

张靖等(2015)[18]对复杂波浪条件下不同管线铺设角度进行了冲刷试验，通过对结果分析得到了复杂波浪条件下海底管线相对冲刷深度公式，如公式(11)所示。

(11)

式中,S为冲刷深度;H为波高;D为管线直径;θ为管线铺设角度。

杨少鹏、拾兵(2018)[19]利用流体的连续性条件，以前人的研究结果为基础推导出了安装阻流器且有间隙情况下冲刷稳定时的冲刷深度计算公式，如公式(12)所示。

(12)

式中,S为管道及床面的间隙;D为管径;Y+Y1为驻点与管线底端的距离;u0为管线中轴上初始行进流速;ub为冲坑内流速;m，n分别为冲坑内和初始断面上的流速分布指数。

冲刷实际上就是泥沙起动后的一系列运动，经过专家学者的研究，粘性沙与非均匀沙的冲刷起动均取得了丰硕的成果，但泥沙起动受力中的粘性力表述目前还未有公认的表达式，且对于非均匀沙分级起动也没有确定的表达式。在实际工程中，泥沙粒径、水流条件及水深等因素均会对冲刷产生不同程度的影响，因此在使用中还需要具体情况具体分析。

3 海底水平管线冲刷悬空与动力响应研究

3.1 冲刷悬空研究

3.1.1 物理模型试验研究

研究的完善为开展物理模型试验提供了一定的基础。物理模型试验相对于其他技术手段研究要求较低，操作较为简便，结果也较为直观。相关研究专家主要基于波流水槽对不同水力条件下海底管线涡激振动、水动力特性以及冲刷防护等方面进行了研究。

常留红(2014)[17]通过水槽定、动床试验，对不同作用角的水流、波浪或波流耦合作用下管线周围的三维水动力特性及其局部三维冲淤演变规律进行研究，揭示了作用角对管线周围水动力特性的变化规律。鲁友祥(2015)[20]对潮流作用下管线的冲刷进行研究，发现重现期为10 a的潮流会使管线自埋，而重现期为100 a时管线会出现局部冲刷，对管线的铺设与防护具有指导意义。谢英等(2017)[21]通过水槽模型实验，同时利用传感器及数据采集系统，分析得出了冲刷坑长度的半理论半经验公式，如式(13)所示。

(13)

式中,l为冲刷坑长度，m；D为管道外径，m；(l/D)max=2.5；K2为动量差的量度。

杨少鹏、拾兵(2018)[19]研究了恒定流作用下海底管线是否安装阻流器以及不同间隙比作用下海底管线的冲刷深度的变化规律。Deniz等(2016)[22]在波浪加水流的水槽中将试验分为两个阶段，一是由纯水流引起的初始冲刷，然后由纯波浪(规则或不规则)引起的回填，以此研究管道下方泥沙的回填效果。

为研究不同管道结构时波浪对管线局部冲刷的影响，Yang等(2019)[23]研究了波浪作用下子母管道在不同因素下的冲刷坑的冲刷深度和宽度，得出在相同的试验条件下，子母管周围的平衡冲刷深度大于单个主管周围的平衡冲刷深度。

物理模型试验作为一种重要的研究方法，上述国内外学者通过物理模型试验对海底管线冲刷进行了详细的研究，可以通过测得的数据为后续的数值模拟和理论分析提供验证，以证明试验结果的可靠性，但容易受到研究手段、试验场地和仪器以及人为因素的影响。

3.1.2 数值模拟研究

近些年来，针对物理模型试验某些方面的不足，冲刷问题的数值模拟研究具有成本低、操作简便等优点，逐渐成为研究海底管线冲刷悬空问题的主要方法。

Zhu等(2013)[24]提出了CFD建模和仿真法研究在沙质海床附近安装扰流板的海底管道周围的水流，通过一系列数值模拟比较了几个重要参数，例如压力系数、速度、涡度等，分析扰流板高度和管与海底之间的间隙对流动特性和海底冲刷的影响。刘延明(2013)[25]通过建立数值模型，研究分析了管道直径以及来流速度对海底管线最大冲刷深度的影响。Liu等(2014)[26]提出将k-ε二维湍流模型用于模拟海底管道周围流场和压力场，模拟局部冲刷变化。结果表明，来流速度与冲刷深度成正比，数学模型能较好地模拟海底管道脱离床面前后管道周围局部冲刷的状况。

宋坤(2016)[27]以某油田平管悬空段为例，对波、流及波流共同作用下不同海床上的悬空段海底管线进行了受力分析，为实际工程中床底对管线受力影响提供依据。利用Visualstudio编制了海底管线极限悬空长度的计算软件，为海底管线的悬空治理提供参考。

许文兵等(2017)[28]利用水动力-泥沙冲刷耦合模型，对往复流作用下海底管线的冲刷做了进一步研究，表明往复流相对于恒定流引起的管道冲刷深度会减少20%。

李昌良等(2018)[29]研究了不同阻流器对管道冲刷以及自埋的影响，通过Fluent软件模拟，分析得出了阻流器高度在D/8-D/4，安装在管线正上方时，有利于实现管道自埋；在30°时，管道下方冲刷速度最快。史舒婧等(2019)[30]提出在Fluent软件中使用UDFs，通过建立三维冲刷数值模型来模拟海底管道周围泥沙冲刷过程，经过与物模对比发现该过程能够准确反映海底管线下方的冲刷规律和流场变化情况。

Hu等(2019)[31]使用耦合CFD-DEM方法考虑动态侵蚀过程中流体与固体颗粒之间的相互作用力，研究两条管道之间的间距和水流速度对管道周围局部冲刷的影响，还得出冲刷深度高度依赖于行近水流速度并与之成正比，在相同的行近水流速度和不同的间隙比下，平衡床的分布是相似的。

上述国内外学者通过数值模拟的方法对海底管线冲刷问题进行了详细的研究，该方法具有可靠度高，受外界因素影响小等优点，可以对多种复杂条件下海底管线的冲刷进行模拟。

3.2 涡激动力响应研究

海底水平管线悬空会直接受到波流等海洋环境的影响，在海洋环境作用下将发生振动，造成海底管线的失稳甚至破坏，威胁海上油气资源的安全。探讨悬空海底管线的动力响应问题，可为海底管线的安全性评估提供科学依据，保障海底管线的安全运行。

沙勇(2007)[32]利用弹性动力学方程、不可压流体纳维斯托克斯方程和连续方程，通过对有流悬跨管线内部的流体特征分析发现管内流速增加，管线振动过程中管内压力波动增加，流体与结构相互作用更加强烈。沙勇等(2009)[33]通过悬跨弹性海底管线涡激振动试验研究，得出在不同相对悬跨高度e/D情况下，悬跨管线涡激振动强度均随折减速度Vr的增加而增加；悬跨管线涡激振动强度不随相对悬跨高度e/D单调变化。

陈博文(2011)[34]通过ABAQUS有限元分析软件对水上空管试验模型进行了正弦波和ElCentro模拟地震波输入下的动力分析，结果与其试验结果基本吻合，说明ABAQUS能较好的模拟地震波输入下管道的动力响应问题。

张敬花(2014)[35]经研究发现在地震和波浪作用下时，悬跨管线动力响应的峰值均出现在跨中，向两端逐渐减小；同时研究了端部支撑类型对悬跨管线动力响应的影响，当管线端部支撑类型为铰接时，各点的变形位移明显大于端部支撑为固接的情况。

赵恩金、拾兵等(2016)[36]对带有导流板的海底管线冲刷过程中产生的涡激振动导致的影响进行了分析，利用ANSYS软件对不同导流板高度下，管线周围的流场、压力场等进行了数值模拟分析，给出了安装导流板的振动响应对管线自埋的影响程度，导流板高度与管径之比为0.375时，有利于管线自埋。

Zhai等(2018)[37]利用RANS和Biot方程，对管道周围不同的土壤动力响应、沙质海床中的规则波进行了研究，研究表明管道周围孔隙压力幅值先增大后减小，最后随着回填区厚度的增大而增大。当回填深度为D时，海床孔隙压力最小;当回填深度为0时，海床孔隙压力最大，即回填深度为D的管道失稳的可能性小于完全回填管道失稳的可能性。管道周围孔隙压力的振荡幅度增大在不同的回填深度下，从管道底部到管道顶部，波浪引起的应力传递到土床的应力随着深度的增加而减小。同时，通过土体深度测得的孔隙压力表明，孔隙压力振幅随填土材料中位直径和深度的增大而增大。

姜文全等(2018)[38]采用ANSYS软件流固双向耦合数值模拟方式研究不同夹角安装导流板的海底管线附近压力、流场、管线所受升力、拖曳力等因素对管线下沉自埋及振动的影响。Zhang等(2019)[39]基于Herschel-Bulkley模型，使用计算流体力学(CFD)方法模拟了海底滑坡在各种冲击角θ下对铺设或悬挂的管道施加的冲击力，提出了计算海底管道轴向阻力和法向阻力系数的方程，为海底管线路由选择和管道设计提供了依据。

Yang等(2019)[40]通过Fluent模拟研究了新型海底子母管线的流场和压力分布、升力及拖曳力系数、平衡冲刷程度(例如深度和宽度)等一系列参数，表明新型子母管道与典型的子母管相比尾涡流强度及冲刷深度均较小，这种新型的子母管道可以有效减小冲孔的深度和宽度。

在研究过程中，由于试验设备的限制，在试验过程中考虑的因素也有限，虽然在计算过程，可以通过有限元软件研究管线内部流速变化、管壁厚度变化以及地震波变化等因素对管线响应的影响，但其准确性还有待确认，需进一步优化试验设备，以便进行验证。

3.3 悬空临界长度

水平海底管线的悬空长度是决定管线破坏的主要因素，悬空管道越长，管道越容易发生破坏。王维等(1996)[41]通过分析海底悬跨管道的工作应力和基于梁的静强度条件，推导出了半冲刷长度l的公式，如式(14)所示。

(14)

式中,φ(Lα)为弯矩修正系数的函数值，取1.333；Lα为约束性质系数，取4.732；[σ]为管材的许用应力，MPa；W为管道截面的抗弯截面模量，m3；q为管道及管内介质的重力和海流冲刷力合成的均布载荷，kN/m。

相关专家学者从涡激振动以及应力的角度出发对海底管道悬空临界长度进行研究，有利于提高管线悬空临界长度计算的适用性，为管线防护提供合理的建议。

4 海底水平悬空管线的动力调整

目前我国正处于已建管线的维护和新建管线建设的关键时期，管线的安全问题将直接影响我国海上石油产业的发展。调查显示，海底管线失事主要是由波流冲刷引起的海底管线悬空。国内外专家学者研究表明，管线所处的动力环境越弱，越有利于管线稳定。海底悬空的动力调整主要从以下几个方面出发：降低管线周边流速，形成淤积环境；增加海床抗冲能力，抑制悬空恶化；降低管线位置，处于弱动力环境；增加床面抗冲流速，加速管线自埋等。

4.1 降低管线周边流速，形成淤积环境

采取相应的措施，使得来流流速在管线附近降低，使携带的泥沙沉积下来，形成淤积环境，从而对管线起到保护作用，如仿生水草覆盖法，通过水草阻流作用促进泥沙的淤积。

人工草最早出现于20世纪80年代中期的英国，最初用于管线的无沟敷设。近些年来，人工草已经应用于海床防护和海底结构物基础的防护，以防止基础冲刷，加固海床以及促进泥沙淤积的作用，并且具有很强的适应性。

吕明春(2008)[42]首次提出仿生海草技术，实践表明该方法能够有效解决滩海海底管道悬空问题，获得了较好的社会效益和经济效益。文世鹏等(2008)[43]对防冲刷仿生海草防护技术进行了更为系统的分析，考虑了仿生海草的柔性黏滞阻尼作用，减缓了海床的冲刷作用。赵冬岩(2008)[44]从海底管线冲刷机理入手，提出了仿生防护措施——“人工草”固定法，通过数值模拟与物理模型试验对该方法进行了验证发现该法能够对悬空管线起到防冲促淤的作用。崔华(2014)[45]分析了埕岛海域海底管线裸露、悬跨的原因并做了一定的防护研究，提出在海底铺设仿生草的方法，发现治理区有明显泥沙淤积现象比例为89.66%，泥沙淤积厚度0.03～1 m。梁爽等(2014)[46]通过对一次悬空和二次悬空的原因进行分析，提出利用高分子材料仿生草叶片的柔性黏滞阻尼作用减缓流速降低水流的携沙能力，以达到减小冲刷和保护管线的目的。

但该方法仅适合周边有泥沙输移且来沙量较大的海域，反之，仿生草丛内缺少泥沙沉积，就起不到防护作用。

4.2 增加海床抗冲能力，抑制悬空恶化

增加海床颗粒的抗冲能力，能够有效减少波流对海床的冲刷，从而可以抑制海底管线的悬空，如抛填沙袋、碎石法。在悬空管道及周围一定范围内抛填碎石和沙袋，使得悬空管线下方填满石块、上方布满沙袋，能够有效减少波流对海床的冲刷，可以抑制管线的侧向摆动，阻止管线悬空的继续恶化。该方法适用于管道底部悬空不是太高且没有漩涡冲刷的情况。但该法可靠性不是很高，碎石和沙袋被冲走后有二次悬空的可能。随着研究的进展，专家也对该方法做了进一步优化，如熊文海(2009)[47]突破以往沙包堆砌的方法，采用钢筋网使水下的砂袋成为一个整体，降低了沙袋整体倒塌的概率，对管线起到更好的保护效果。梁富浩等(2011)[48]以平湖油气田岱山近岸段KP2.6为例，通过比较海底管线的各种防治措施，提出了“砂袋悬空回填与仿生草永久性冲剧防治”的方案，不仅能防止管线的摆动还能起到促淤的作用，在含沙量较高的海域能较好防止二次冲刷。但该法可靠性不是很高，碎石和沙袋被冲走后有二次悬空的可能，“客沙”也会被水动力搬运到其他位置，无法形成长效防护机制。

4.3 降低管线位置，处于弱动力环境

在海底管线铺设完成后或铺设过程中，将管线埋到海床下一定的深度，使管线处于十分弱的动力环境中，可以减少海流对管线的冲刷。李国宝(2013)[49]根据南堡浅海海底管线悬空的成因及当地的自然地理条件，提出了后挖沟技术对海底管线悬空进行治理，对未来浅海区域海底管线悬空问题的防治具有指导意义。当管线悬空后，可以采取相应的措施对管线进行覆盖，从而使管线处于弱动力环境中。刘锦昆(2014)[50]以胜利油田为例，通过对不同水质点运动速度、不同悬空长度、悬空高度下海底管道悬空段涡激水平振动及垂直振动的动应力幅值的分析，并进一步对海底管线悬空段的疲劳寿命进行预测。但该方法的施工与水下控制较为困难，仅适合典型悬空管线防护，对普遍性的海底悬空管线的防护较难实现。

4.4 增加床面抗冲流速，加速管线自埋

在管线上安装spoiler可以改变管线周围的流场和压力场，从而使管线的受力发生变化，可以增加床面的抗冲流速，加速管线的自埋。国外对spoiler的研究起步较早，Hulsbergen(1986)[51]，YM.Chew(1993)[52]已经对管线上安装扰动器后海底管线的埋设深度和冲刷速度做了部分研究。在国外提出刚性导流板(spoiler)的基础上，韩艳(2010)[53]提出在管线顶部安装柔性导流板能够促使管线下沉和自埋，在管线底部安装柔性导流板可以减小甚至阻止管线冲刷，达到管线防护的目的。杨立鹏(2012)[54]通过对波浪作用下管线底部安装柔性导流板的研究，得出了不同条件下管线冲刷的临界压差和柔性导流板长度的临界值。张宗起(2016)[55]通过模拟波浪作用下安装阻流器海底管线的冲刷及自埋，分析波浪对管线的作用力，表明海流是管线自埋的主要作用力，对海底管线的悬空防护具有一定的指导意义。综上，导流板(阻流器)适合易冲易淤的沙质或泥质海床，且动力方向与管线正交；如动力方向与管线路由一致或海底局部有耐冲物质，此段管线裸露或悬空的几率很大，需要进行专门的防护设计。

4.5 其他前沿调整措施

从生态的角度出发，T. Bond等(2019)[56]提出将海上平台以下的管道结构部分经过轻微的改造，使之成为不同结构要素的鱼类栖息地，在结构内建立栖息地不仅能够减少海流对管线的冲刷，还有助于了解现有人工鱼礁作为鱼类栖息地的使用情况。D.L. McLean等(2020)[57]利用行业收集的遥控车辆视频评估沿澳大利亚联邦穿过海底天然气管道(深度为56～82 m)的鱼类种类的丰富度，说明该管道对鱼类的丰富度具有积极影响，同时鱼类的存在缓解了海流对管线的冲刷，实现了良性的生态循环。因此，基于海底管线的冲刷悬空动力机制，开展组合式、生态型人工礁体对海底强侵蚀悬空管线的动力调整和泥沙回淤机理研究，增强管线自身的可靠性和生态环境的协调性，以保障海底管线的安全运行，已变得十分迫切和重要。生态礁体的绕流、缝隙流和尾流结构，易于将来沙捕捉到冲刷坑内的弱动力区，实现泥沙回淤，具有 “捕沙器”的功效，可扭转悬空高度不断加剧的不利局面。生态礁体的布设，利于海洋生物的聚集和生长，具有“人工鱼礁“作用，反过来，鱼类的聚集和丰满度的提升，易于管线周边泥沙扰动-输移-再沉积，形成生物活性功能循环利用之良性机制。

5 结论

本文全面阐述了海底水平管线悬空的研究现状以及近些年来取得的最新研究成果，总结了不同水力条件下的泥沙起动公式以及管线相对冲刷深度的计算经验公式，对近些年来管线冲刷悬空以及悬空管线的动力响应研究进行概括，最后，总结了海底水平管线动力调整的方法。通过对海底水平管线悬空机制与动力调整方法研究的总结，得出了以下几点认识：

(1)在研究海底水平管线悬空机制时，由于海洋环境是十分复杂的，海底管线悬跨的原因也是多种多样的，对于海底埋设的管线，除要考虑海流的冲刷外，还应考虑管线与海床的相互作用。

(2)现有关于海底管线冲刷平衡深度的计算公式主要基于试验，当试验条件发生改变时，有些公式便不再适用，具有明显的局限性。通过对众多经验公式分析表明，尚未发现通用的公式。因此，需要更全面的研究海底管线的冲刷机理。

(3)通过物理模型试验，数值模拟和理论分析对波流作用下海底管线的冲刷悬空机理以及管线悬空的防治做了很多研究，但海底管线冲刷是关于海底管线、海床和水流之间非常复杂的三维相互作用的问题，对于不同条件下海底管线的冲刷机理还有待进一步研究。

(4)在动力响应的研究过程中，由于试验设备的限制，试验时考虑的因素也有限。在实际计算中可以通过有限元软件研究管线内部流速变化、管壁厚度变化以及地震波变化等因素对管线响应的影响，但其准确性还有待确认，需进一步优化试验设备，以便进行验证。

(5)尽管目前提出了很多悬空管线动力调整的措施，但尚未找到真正最有效的调整方法。从海洋生态角度出发，研究表明管道对鱼类的丰富度有积极的影响，同时鱼类的存在缓解了海流对管线的冲刷，日后可以朝海底管线与人工鱼礁相结合的角度研究，建立良性的生态循环系统。