等距离海洋划界模型研究

张建辉，张学峰，肖 利，陈韶阳*

(1.天津大学 海洋科学与技术学院，天津 300072；2.国家海洋信息中心，天津 300171)

引 言

海洋划界最早源于陆地上河流或湖泊的水域划界问题。19世纪20年代沿海国开始主张领海权利后，划界争端才延伸到海上。[1]1994年11月，《联合国海洋法公约》(以下简称《公约》)生效后，沿海各国纷纷扩大本国海洋权利主张的范围，海洋划界由解决两国领海划界扩展为解决两国领海、专属经济区和大陆架的划界。虽然《公约》提出了实现公平划界的目标，但是没有明确具体的划界方法。因此实践中出现了多种划界方法，如等距离/中间线法(以下简称“等距离法”)、角平分线法、垂直岸线法、方位线法等，沿海国家采用哪种方法主要取决于可主张的最大海域范围，但最为常用的是等距离划界方法。

采用数学几何原理实现等距离划界方法的数学模型称为等距离划界模型。早期由于没有计算机，制图人员采用直尺、圆规、量角器等作图工具在纸质海图上完成界线绘制[2]。20世纪70年开始，国外开始研究计算机等距离划界技术[3]。随后，国内外相继出现“三点法”[4,5]、“水线法”[6]、“弹性圆法”[7]、“Voronoi图法”[8]等划界模型，计算效率和空间精度不断提高。针对不同划界模型产生的海洋边界，WANG Degang等人研究基于AHP—熵权法的海洋划界方案模糊综合评价方法[9]。国内外对不同划界方法的适用场景、计算精度以及结果比对分析等尚未开展系统研究，特别是国内学者对“三点法”划界模型的研究不足。我国战略全局高度的陆海统筹战略，在空间范围不仅涵盖领土、内水、领海、专属经济区和大陆架，还应包括公海、国际海底区域和南北极[10]。因此，结合当前我国周边海洋划界实际需求以及未来全球公域和极地战略利益拓展长远考虑，研究符合国际通用技术标准的高精度等距离海洋划界模型十分必要。

1 等距离划界方法

1.1 法律概念

与1958年《领海及毗连区公约》的定义基本相同，《公约》第15条规定了相邻或相向国家之间的领海划界方法，即彼此没有相反协议的情形下，采用等距离/中间线进行划界，但如因历史性所有权或其他特殊情况可采用不同的划界方法。《公约》定义的中间线为“每一点都同测算两国中每一国领海宽度的基线上最近各点距离相等”。与1958年《大陆架公约》关于大陆架划界使用“中间线”法不同，无论是两国之间专属经济区划分还是大陆架界定，《公约》都没有明确具体的划界方法，只是要求“应在国际法院规约第38条所指国际法的基础上以协议划定，以便得到公平解决”[11-13]。

1.2 几何意义

不论两国海岸是相邻或者相向，几何学上等距离法生成的界线实质均为等距离线。海岸相向国家之间产生的等距线称为“中间线”，海岸相邻国家之间产生的等距线称为“侧向线”[14]。对于海岸相向国家，元哲起[15]分析了几何平面上推算等距离线的数学原理(图1)：一是对于A、B两个岛屿国家，岛屿可以等效为平面上的两点，两国等距离线为两点之间垂直平分线，此时点P到点A和点B距离比k=1；当比例值k不为1时，垂直平分线演变为等比例曲线，即为半径不断变化的圆；二是对于A为岛屿国家、而B为大陆国家时，岛屿岸线和大陆岸线可以等效为一个点和一条直线。当k=1时，等距离线是一条以A为焦点、B为准线的抛物线；当比值k<1时，等比例线是一条以岛屿国家为焦点、大陆国家海岸为准线的椭圆曲线；当比值k>1时，等比例线是一条以岛屿国家为焦点、大陆国家海岸为准线的双曲线。按照公平原则，在海洋划界实践中，小岛屿国家所享有的划界权重比大陆国家划界权重低，因此不可能存在等比例值k>1的情况，也就是说不存在双曲线性质的界线。

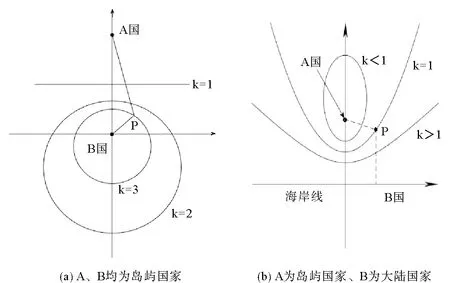
图1 等比例线的几何意义(根据文献[15]绘制,p83)

Langeraar[16-17]阐述了海岸相邻两国之间等距离划界的几何意义。理想情况下，相邻两国海上边界实质为垂直两国岸线的向海延伸线。如果近岸存在岛屿，则受到岛屿影响的那部分边界的实质为抛物线，等距离划界的结果应为直线段和抛物线段的组合。但是，由于一方海岸存在岛屿，简单套用等距离划界方法会使不存在岛屿的一方利益受损，从划界公平考虑，一般会按照等比例进行划界，最终形成的边界为直线段和椭圆曲线的组合。

如图2所示，P、Q为海岸相邻国家，近岸附近存在P国岛屿O，A点为两国陆地边界终点，ABC为垂直两国海岸的垂线，曲线BD及虚线部分为以岛屿O为焦点、两国低潮线为准线的抛物线。考虑到P国岛屿的存在，应用等距离线会对Q国产生不公平结果，因此可以分别赋予两国海岸和岛屿不同的划界效力再进行海域划分。

图2 海岸相邻国家的等距离线(根据文献[17]绘制,p15)

如图3所示，按照界线上某点到P国与Q国的距离比(分别为选取0.9和0.85)推算等比例界线，其中AL为两国大陆海岸之间等比例线，椭圆曲线LN为Q国大陆海岸与P国岛屿O之间的等比例线。

图3 海岸相邻国家(一方存在岛屿)的等比例线(根据文献[17]绘制,p15)

在实际的海洋划界中，划界双方的海岸不是简单的直线，而岛礁也并不是坐标点，而是形态复杂的几何图形。特别是对于大尺度空间的专属经济区和大陆架划界，也必须考虑地球曲率影响，最终形成的等距离界线不可能是简单的平面直线段和曲线，而是更为复杂的椭球面曲线组合。

2 主要等距离划界模型

2.1 三点法模型

早在1937年，美国地理学家BOGGS[18]介绍了一种在纸质地图上手工绘制等距离线的方法(也称“图解法”)，用于确定密歇根湖水域的中间线。如图4(a)所示，海岸相向国家之间绘制等距离线过程为：首先，从A国和B国海岸线上寻找距离最近的A1点和B1点作为起始点，作A1B1的垂直平分线p1q1；沿着该垂直平分线向右移动，在双方海岸上寻找下一个距离最近的点，即A国海岸上的一点A2；作A2B1的垂直平分线p2q2，与p1q1相交于M1点，M1点满足到A1、A2、B1距离相等，且距离两国海岸最近，故M1为所求等距离点；继续沿着p2q2向右移动，在双方海岸上寻找下一个距离最近的点，即B国海岸上的一点B2；作A2B2的垂直平分线p3q3，与p2q2相交于M2点，M2点为第二个等距点；接着继续向右寻找余下等距点，直到右边的划界海域被完全覆盖；然后按照相同方法，沿着A1B1的垂直平分线p1q1向左方寻找划界海域的等距点，直到左侧海域的所有等距点也全部找到；最后，从左到右依次连接各等距点，即为所求等距离线。海岸相邻国家之间的等距离线构造过程与上述方法类似，只不过首先确定海上边界的终点，然后再向陆地一侧依次确定余下的等距点，绘制过程如图4(b)所示。

图4 国家之间等距离线绘制方法

1976年，美国地理学家ROBERT等[19]设计了在地图投影平面上“三点共圆”的方法求解中间线的计算机程序，如图5所示。基于这一思想，1987年加拿大的CARRERA提出了基于地球椭球面的中间线计算模型，并将其称为“三点法”模型[20]，即通过在双方岸线上寻找三个划界基点组合(一方取1个，另一方取2个)，首先在地图平面上利用“三点共圆”计算圆心点作为等距离线的坐标拐点近似值，然后在地球椭球面上进行迭代计算，最后求出满小于指定误差的精确值。此后，该模型成为计算海域中间线/等距离线的经典方法，国内外学者也主要集中在对该方法的研究或改进[21-24]。“三点法”模型实质上海域空间Delaunay三角剖分问题，通过构造Voronoi图提取海域中间线[25-26]。在前人基础上，KASTRISIOS等[27-29]先后研究了基于Voronoi图的海域外部界限与中间线一体化划界技术，提出了在地球椭圆体上生成Voronoi图的方法。

图5 三点法模型示意图

“三点法”划界模型起源于手工制图时代，特别适合在地图平面上手工快速绘制“中间线”，解决了早期海洋划界的技术难题。因此，该方法一经出现，就在国际海洋划界实践得到应用，其基本概念也被后来的国际海洋法相关条款所吸收。虽然随后出现多种海洋划界模型，但是该模型一直是国际司法或仲裁机构、争端国家普遍使用的方法。该模型运行效率及生成的等距离线主要与双方海岸最外缘选取的划界基点数量有关，划界基点越多，模型运行效率越低，生成的等距离线形态也就越复杂；反之，计算速度越快，边界形态就越简单。此外，在某些情况下，距离线并非严格几何意义上的几何图形的等距离线，因为某些等距离点可能远离三角形中心或者位于三角形之外。[30]

2.2 水线法模型

水线法[31]是西方18世纪中期至20世纪常用的一种制图方法，它的基本思想是通过连续追踪一定间隔距离的平行线来绘制和表达水域特征。基于这一思想，CHRISTENSEN[32]设计开发了Waterlining and Medial-Axis(简称“WL & MA”)计算机程序，在地图投影面上自动计算海域等距离线或中间线。如图6所示，海岸相向国家之间推算海域等距离线的过程为：首先，从A国和B国各自海岸线开始，分别以间隔为d1、d2的距离追踪绘制两国海岸平行线A1、B1；然后，再从A1、B1开始继续追踪绘制两线间隔距离为d1、d2的平行线A2、B2；以同样的方式，继续追踪两侧平行线，直至两侧形成的平行线An、Bn相交；然后，寻找A1、A2、A3、……、An分别与B1、B2、B3、……、Bn相交的点，并记录为M1、M2、M3、……，Mn；最后，从左到右依次将各交点连接起来就是所求等比例线。如果双方追踪平行线所用的间隔距离相等(即d1=d2)，最后生成的线就是等距离线。海岸相邻国家等距离线求解过程与此相同。

图6 “水线法”示意图

国内学者彭认灿[33]对水线法进行了深入研究，在分析水线法存在问题的基础上提出了地球椭球体缓冲区构建技术的等比例水线法海洋划界模型，并给出地球椭球面等比例线求解的关键步骤。在此基础上，董箭等[34]、宁方辉等[35]给出了较为详细的实现算法，实现了地球椭球面高精度缓冲区边界相向逼近求交来计算等比例线。该方法很方便地改成等比例线计算，也比较容易移植到地球椭球面。但是迭代计算平行线，特别是当生成的平行线距离相互接近时，需要不断缩小绘制间隔距离进行反复试探才能找到合适的交点。因此，该模型运行效率较低，如果转换到地球椭球面，效率将会进一步降低。

2.3 弹性圆法模型

1987年，赖宝珍等[7]提出一种基于“弹性圆”的等距离线计算机生成方法，并设计了数据结构和算法。如图7所示，对于海岸相向或相邻国家之间的等距离线计算，“弹性圆法”划界模型计算过程：首先，在两国海岸线上选择距离最近的两点，取两点中点作为等距离线计算的起点；其次，从起点出发，以一定步长沿着双方海岸的大致方向寻找下一个点。如果该点到两侧岸线距离之差小于给定误差，则该点吸收为等距离线上的坐标点。反之，将该点以起点为圆心向某一侧海岸旋转一定角度，重新确定等距点位置；然后，再计算新点到两侧海岸最近距离之差是否小于给定误差。反复调整，直到该点满足误差要求，则吸收为等距离线上的拐点。以相同的步骤确定划界海域范围内所有的等距离线坐标点；最后将各点依次连接，即为所求的等距离线。在地图投影平面上，该方法实质上是一个半径不断变化的圆在两国岸线之间进行连续滚动，并且在滚动过程中始终与两侧岸线保持相切，这一系列圆心所形成的轨迹就是等距离线。之后的相关研究工作主要是针对这一模型进行的改进。后人对该模型进行优化和完善，实现了地球椭球面等距离/等比例线精确计算[15，36-37]。

图7 “弹性圆法”示意图

弹性圆法运行效率以及生成等距离线的形态与等距离点的移动步长相关，移动步长越小，运行效率越低，生成的等距离坐标拐点也越多，最终形成的等距离线形态也趋于复杂。因此，可以根据划界需求合理设置步长取值。“弹性圆法”和“水线法”类似，两种算法都以“线段”为单元计算等距离线。但是与“水线法”相比，“弹性圆”模型具有良好的计算精度和运行效率，生成的线型也具有良好的形态[30]。

3 不同等距离划界模型计算结果比对

现以某海域A国和B国划界为例，说明不同划界模型的计算结果差异。首先，在双方岸线最外缘确定合适的划界基点。如在A国一侧选取14个基点(P1—P14)，在B国一侧选取15个基点(Q1—Q15)。然后，分别采用“三点法”(美国Teledyne公司开发的Caris Limits and Boundaries Module for Base Editor 5.3.1)、“弹性圆法”(国家海洋信息中心开发的海洋划界软件)和“水线法”(海军大连舰艇学院开发的划界软件)分别推算该海域的中间线。如图8(a)所示，采用“三点法”产生的中间线共有20个拐点坐标(M1—M20)，其中M17和M18偏离中间线方向，该软件产生的奇异值应舍弃。调整后“三点法”产生的中间线由18个点组成(M1—M18)，如图8(b)所示。

图8 “三点法”生成的海域中间线示意图

采用“弹性圆法”计算中间线时前进步长设置为12 n mile，“水线法”计算时缓冲半径也设置为12 n mile，由于两者算法产生的坐标拐点较为密集，现仅在图中展示两条中间线，如图9(a)所示。通过对比两条线可以发现：除在A、B两个区域外，两种方法计算的中间线基本一致，坐标拐点多，线型平滑。两种算法在A、B两处产生的差异主要取决相向海岸距离与“水线法”缓冲步长，通过进一步减少缓冲步长，两条线将基本重合。由于“弹性法”和“水线法”结果基本一致，因此我们只选择“弹性圆法”和“三点法”进行比较。如图9(b)所示，“弹性圆法”和“三点法”产生的中间线除在C、D两处较大差异外，其他部分基本重合。两种算法结果差异主要因为“三点法”在C、D两处所依赖的基点数量较少造成的。如果在两处双方基点连线(P6P7、Q11Q12和P12P13、Q13Q14)适当插入基点，“三点法”计算结果将与“弹性法”趋于一致。

图9 不同划界模型计算结果比对

4 讨论

从理论上讲，通过对起算数据插值或合理设置参数，“三点法”、“弹性圆法”和“水线法”均可以产生形态一致的中间线。但是“三点法”生成的中间线更符合《公约》法律意义，起算数据可以是点、线或其组合，适用于正常基线、直线基线或者混合基线情况，大多经过简单调整后就可以被双方所接受。而“弹性圆法”和“水线法”起算数据为“线段”，更适用于正常基线或双方海岸较为平缓的情况，而且需要设置合理的计算参数，最终生成的中间线形态也较为复杂，需要进行大幅度简化，而如何简化又是一个复杂的外交谈判过程。

基于地球椭球面“三点法”模型，Caris、Geocap等国外商业软件实现了高精度的等距离/等比线生成，但是这些软件核心划界算法并不透明，算法效率有待提升，计算结果有时存在奇异值，功能也偏重于几何图形生成和编辑，缺乏划界方案分析、评估和优化等辅助决策能力。目前国内对高精度“三点法”海洋划界模型研究并不充分，核心技术还受制于人。由于涉及国家海洋安全和权益，海洋划界不同于一般地理空间划分问题，应当在国际通用划界技术标准下研究和发展高精度海洋划界方法模型，核心问题包括：(1)高精度的地球椭球面底层空间量算方法。基于地球椭球面的高精度空间量算技术能够为海洋划界提供底层技术支撑，真正实现所有计算与地图投影、比例尺和空间位置无关[38]。(2)高效率的地球椭球面等距点迭代法计算模型。地球椭球面上曲线拓扑关系表达十分复杂，通常先将起始数据的地理坐标转换为平面或球面坐标计算界线拐点的近似坐标，然后在地球椭球面反复迭代法计算满足误差要求的精确坐标。显然，研究基于迭代法地球椭球面等距点计算模型，提升算法计算精度，优化算法运行效率，是实现高精度海洋划界的核心问题。(3)高保真的地球椭球面海洋界线精密展绘方法。实践中国家海上界线由少量界线坐标点组成。由于受地图投影影响，如果在地图上将界线各点直线相连，无法正确表达海洋界线的真实走向[39]。通过对界线各点之间进行大地线插值加密，就可以在地图上准确表达海洋界线实际位置。因此，研究地球椭球面海洋界线精密展绘技术，对准确表达海上界限范围具有重要意义。

5 结论

国际司法或仲裁机构判决的划界案例显示，沿海国最终建立的海洋边界往往是在初步确立的等距离线基础上，经过双方谈判协商对其进行简化和调整，最后形成一条简洁的几何边线。求解严格的等距离线并没有实际意义。等距离海洋划界方法的实现模型有多种，但是“三点法”计算结果更符合《公约》定义，已成为国际海洋划界中普遍使用的方法。国内对地球椭球面“三点法”划界模型研究仍需加强，应结合我国周边海洋划界需求，尽快实现海洋划界核心技术自主化，不仅能够保障国家海洋划界工作安全可控，还可以为全球海洋划界治理能力提升提供中国方案。