多级盘转子装配不平衡量预测与优化

2022-08-30刘洪慧刘亮李明华东晓孙清超

机械科学与技术 2022年8期

刘洪慧,刘亮,李明华,东晓,孙清超

(大连理工大学机械工程学院,辽宁大连 116024)

航空发动机装配质量是保证航空发动机整机性能的重要因素,其中转子不平衡量过大是引起的不平衡力是影响整机振动的关键因素之一。而多级盘转子装配后的初始不平衡量过大,会给后续平衡工艺带来困难,同时在转子出现故障时会产生更大的振动,所以在装配过程中控制初始不平衡量的大小十分重要。

国内外很多学者对此进行了研究,李常有等[1]通过振动信号和不平衡响应信号进行不平衡量的预测。张冬梅等[2]和纪福森[3]通过改进平衡工艺和分步平衡精度控制,有效降低了整机振动。随着研究深入,大家通过圆度仪圆柱度仪测量的跳动数据进行误差分析,Whitney等[4-5]建立了基于齐次坐标变换的公差表示方法。文献[6-10]通过多级转子空间的矢量投影特征实现多级转子直线装配误差传递的分析,文献[11-12]结合偏心偏斜预测方法采用小位移旋量通过齐次坐标变换建立了转子装配精度预测模型。优化方面,曹国茂[13]和李立新等[14]分别利用Powell法和遗传算法对多级盘转子装配相位进行优化,有效降低了不平衡量引起的力和力矩。吴法勇等[15-17]通过分析多级盘转子结构同心度、垂直度与不平衡量的堆叠机理及装配参数对不平衡量的影响关系进行双目标优化,极大降低了装配后的初始不平衡量。

目前对装配不平衡量的分析中存在一定不足。没有考虑实际回转轴线的位置,装配体空间位姿表达不够清楚,对各种不平衡量的分析计算不够清晰,很少考虑位姿引起的偶不平衡量,很少区分装配后转子整体的静、偶不平衡量情况,优化过程没有考虑各零件质心分布情况。

本文使用齐次坐标变换,根据回转轴线的位置确定转子的空间位姿,分析了转子装配后的初始静、偶不平衡量及质心分布情况,得到了多级盘转子装配不平衡量预测模型,然后介绍了一种基于预测模型以初始静、偶不平衡量及质心分布为优化目标的多目标优化方法。

1 不平衡量预测模型

转子在设计上一般都使其相对于回转轴线完全对称,但是由于加工、装配等一系列因素,装配后的转子总不能够实现动力上的完全对称,也就是说存在一定的不平衡量,这种不平衡量一般称作初始不平衡量。由于不平衡量影响因素较为复杂,通常通过平衡机旋转试验(动平衡)来测量,而本文通过实验测试的零件端面跳动及径向跳动数据,以及零件自身的质量、转动惯量等因素计算预测转子的初始不平衡量。

1.1 单件静、偶不平衡量

所有的回转体的不平衡量都能表示成静不平衡量和偶不平衡量叠加的形式,如图1所示,其中质心的偏移形成静不平衡量,零件的偏斜,即基准轴线与回转轴线的夹角形成偶不平衡量。

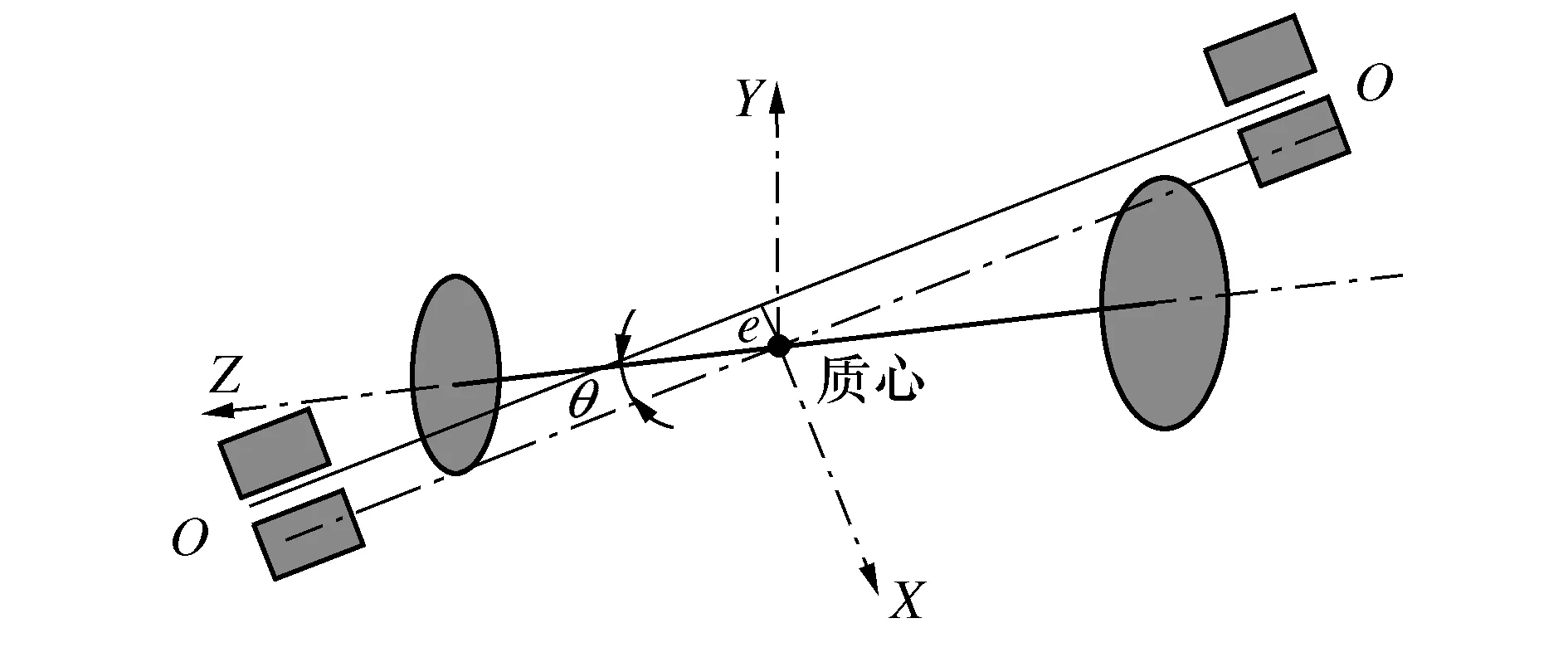
图1 不平衡量类型

静不平衡量[18-19]:静不平衡量等于不平衡质量与该质量中心(质心)到回转轴线距离的乘积,方向与质心相位方向相同。

U=e·m

(1)

偶不平衡量[18-19]:力偶不平衡是由两个大小相等、方向相反的不平衡惯性力所引起的,力偶不平衡量的大小可以表示为

M=mra

(2)

式中:m为不平衡力偶中质点的质量;r为质点到旋转轴的距离;a为两质点垂直旋转轴平面的距离。由于这些参数难以求出,这里使用下面的方法进行计算。

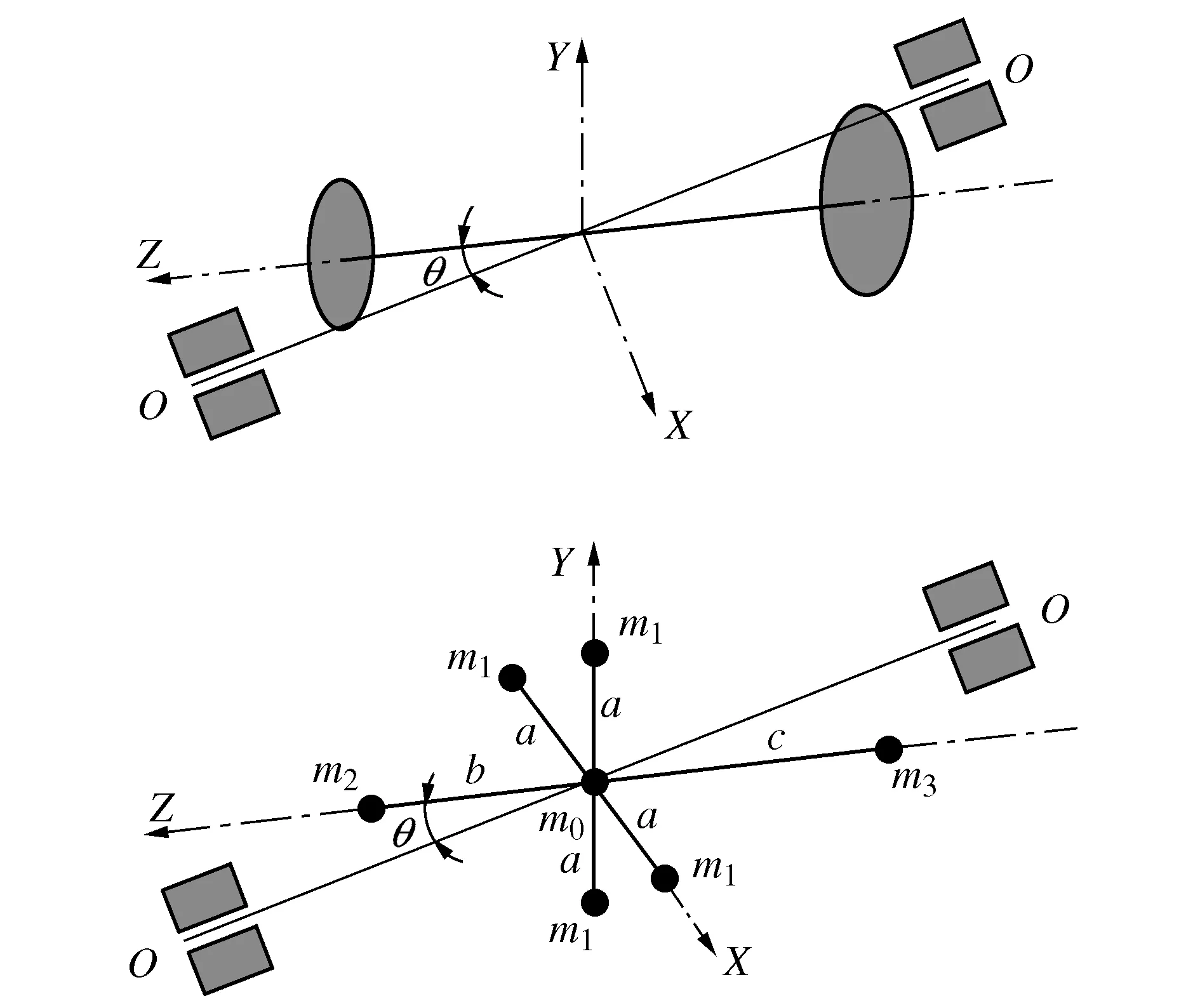
图2 单件偶不平衡量计算

毛荣宝[20]对圆柱体偶不平衡量计算,这里对普通回转体由位姿引起的不平衡量进行推导。应用等效动力系统方法, 用7个质点等效原系统,回转体绕回转轴线一周的情况完全相同,设一周4个点的质量和距离分别是m1和a;理想回转轴线上的两个质点的质量和距离分别设为m2、b和m3、c;中心点质量为m0;各轴转动惯量为Ix、Iy、Iz。使Y轴和Z轴在回转轴线与实际惯性轴线去掉静不平衡量后所组成的平面内,X轴垂直于该平面。

根据偏斜角θ可以求得力偶距m0,进而获得偶不平衡量大小为

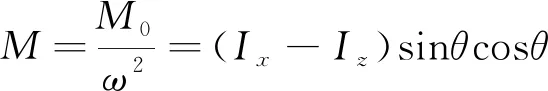
(3)

偶不平衡量方向与去掉静不平衡量后的实际惯性轴线相对回转轴线的相位相同。

1.2 装配体几何精度计算

描述装配体空间位姿的方法有很多,本文采用齐次坐标变换的方法[11]来描述,即用一个4×4的矩阵来表示坐标的变换,即

(4)

单件:对于单件来说可以使用上下两结合面及上下止口圆心连线来表示。通过止口处径向跳动的拟合获得圆心位置;通过结合面端面跳动的拟合获得平面位置。为了更清晰的表示零件,这里通过平移变换使下圆心O1与基准坐标系原点重合,通过旋转变换使下平面与基准XOY平面重合,这样就可以通过表示上零件原点及平面的空间位姿表示这个零件。单件的表征方法如图3所示。

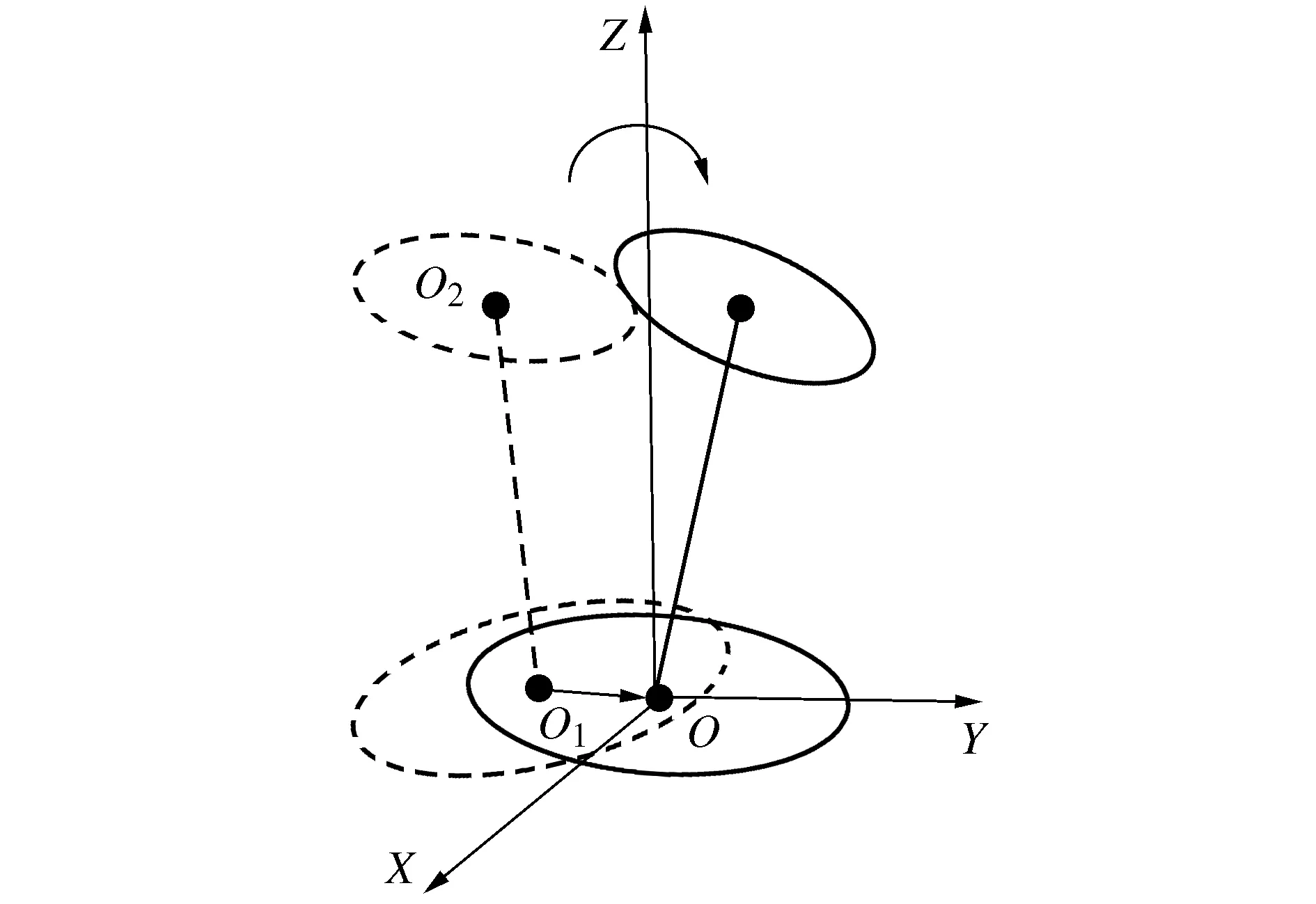
图3 单件的表征方法

单个回转体零件的空间位置和姿态可表示为

(5)

装配体:装配体的空间位姿可以表示成各个单件堆叠的形式,即通过任意一点局部坐标系的位置都能由一级一级的旋转与平移变换得到其对于整体基准坐标系的位置。在齐次坐标变换中即左乘旋转平移综合变换矩阵。若以第一级转子下端面坐标系为整体基准坐标系可以表示为

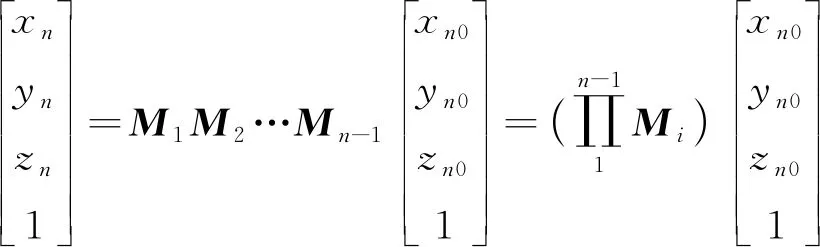
(6)

若考虑装配相位:相当于从第二级转子开始每级转子多乘一个绕Z轴旋转的变换矩阵,即

(7)

此时,第n级转子质心在基准坐标系(即第一级转子下结合面坐标系)下的位置为

(8)

若转换到以回转轴线为Z轴的坐标系,则相当于再左乘一个轴线变换矩阵M0,即

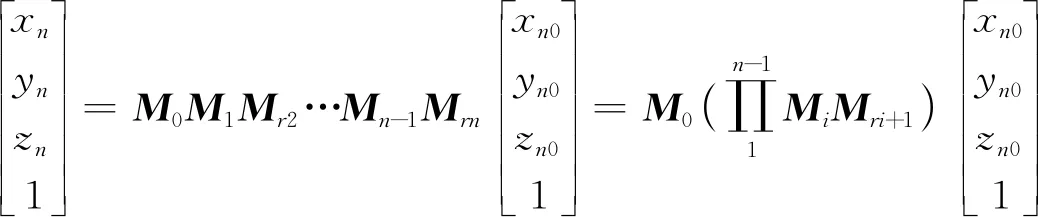
(9)

1.3 整体静、偶不平衡量

整体静、偶不平衡量影响装配后振动的大小,能直接反映装配体的装配质量。本文通过空间位姿、转动惯量等因素对转子装配后的不平衡量进行计算。

这里进行如下假设[14]:

1) 部件的惯性轴为直线,且和单件两结合面的圆心连线重合。

2) 部件的质量分布均匀,即不考虑加工不均引起的不平衡量。

3) 部件是刚性装配,两件结合面处圆心重合。

通过1.1节的静、偶不平衡量计算方法及1.2节中的装配堆叠后的空间位姿可以得到每个单件的静、偶不平衡量,进而可以计算两端轴承处的不平衡质量矩，如图4所示。

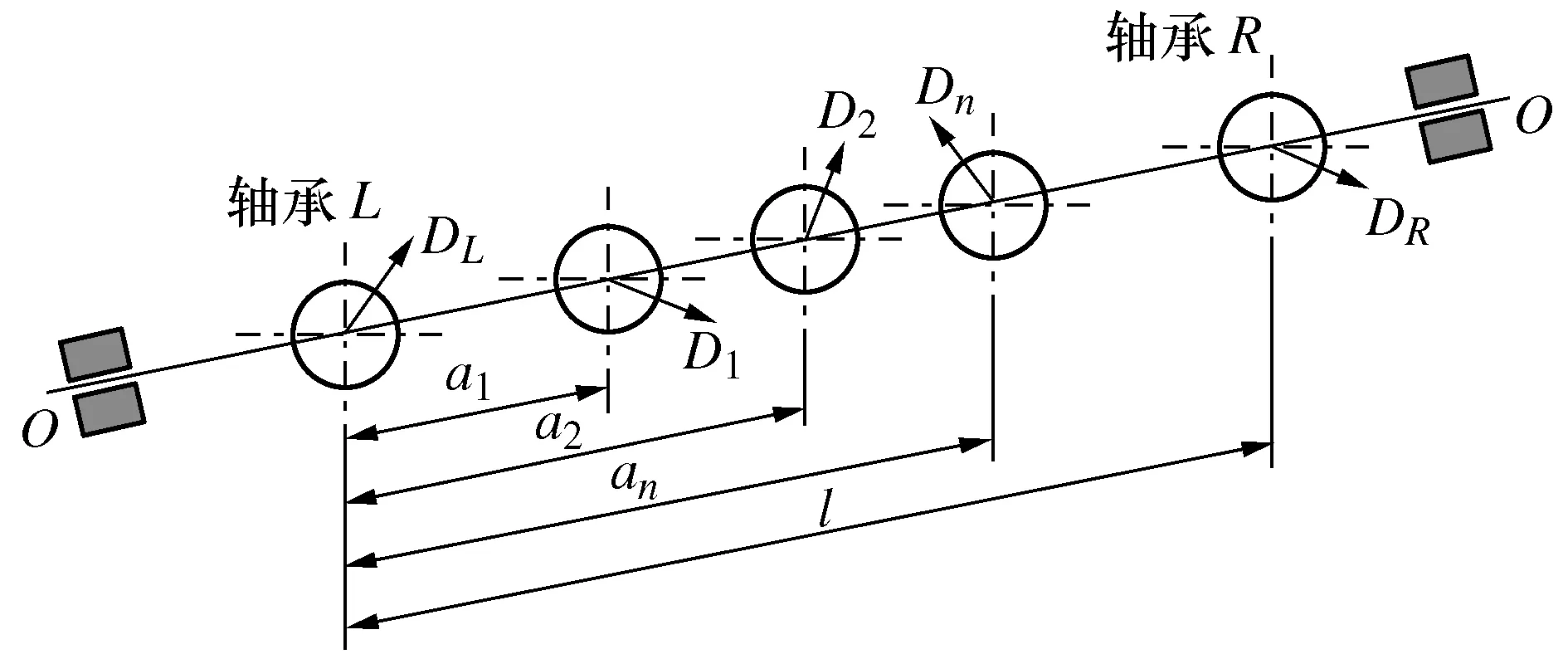
图4 轴承处不平衡质量矩计算

将每一级转子静不平衡量Dn矢量分解到左右轴承L、R处,然后叠加:

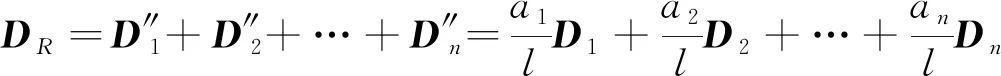
(10)

式中：an为转子质心距左端轴承的距离;l为两轴承之间距离。

将每级转子偶不平衡量C1矢量相加分解到两轴承位置L,R得到质量矩为:

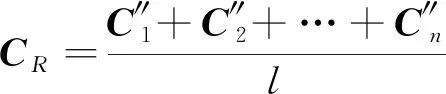
(11)

则每个轴承处的质量矩为:

EL=DL+CL

ER=DR+CR

(12)

左右两轴承处的不平衡质量矩,可以分解为方向相同的静不平衡量,和大小相等方向相反的偶不平衡量,即对整个装配体的静、偶不平衡量。

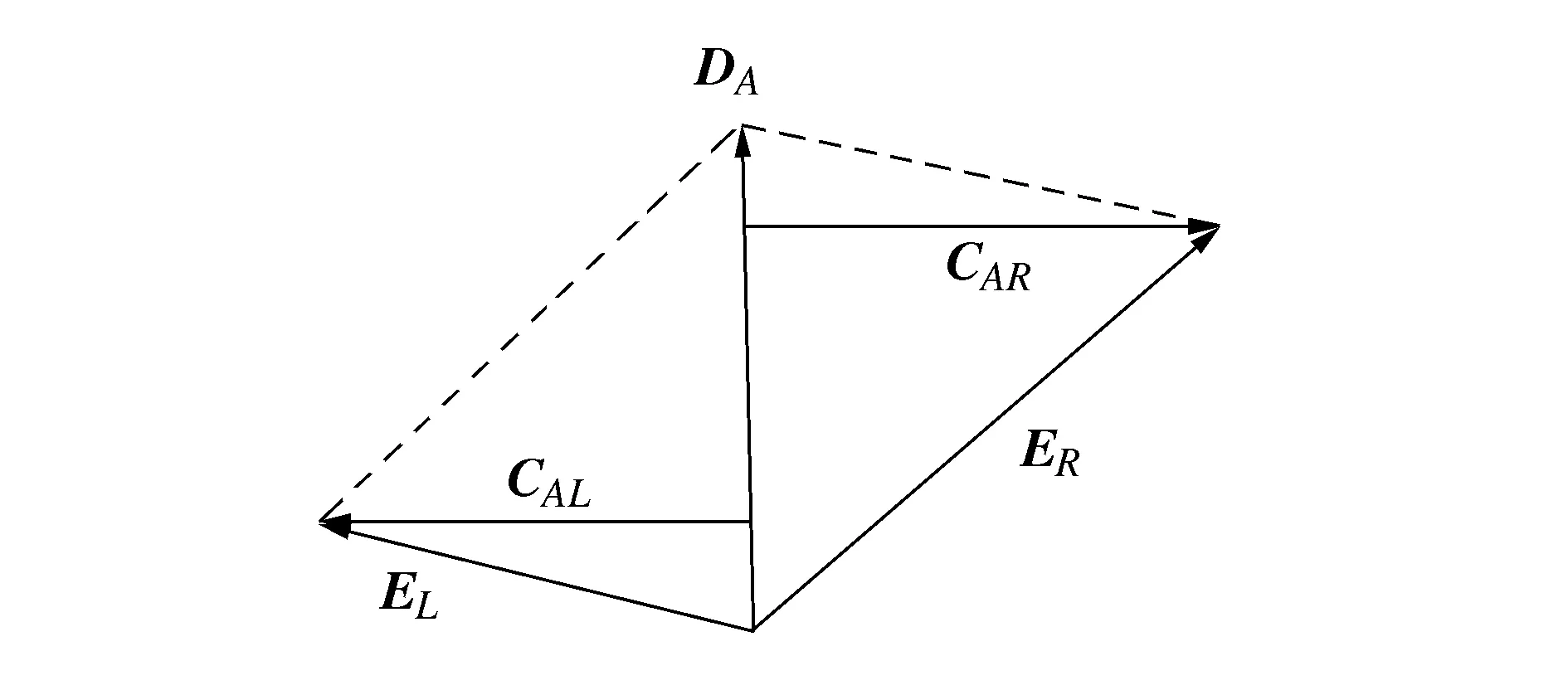
图5 整体不平衡量计算

对整体静不平衡量表示为

DA=EL+ER

(13)

对整体偶不平衡量表示为:

CAL=(b-z)EL+(a-z)ER

CAR=(z-b)EL+(z-a)ER

(14)

式中:z表示整体质心位置;a、b表示左右两轴承位置;CAL和CAR大小相等方向相反,不平衡量相位使用其中CAR的方向表示。

1.4 质心分布情况

质心分布情况表示装配体各个单件质心位置的分布范围,质心分布情况不止通过影响装配体不平衡量影响装配质量,同时在工作的过程中,由于质心不在同一条直线会给各零件结合面带来附加的弯矩,其次质心分布更分散在转子在工作过程中如果发生变形时还会引起较大的附加不平衡量。所以在装配体不平衡量预测的同时,各单件的质心分布情况也值得考虑分析。

参考国际标准ISO1101-2012[21]中同轴度误差的定义方法,以基准轴线(根据实际情况以回转轴线为基准轴线)为轴线,以包容各质心截面提取质心点的最小圆柱面半径t表示质心分布情况。

t=max(δ1,δ2,…,δn)

(15)

式中δ表示质心到基准轴线(回转轴线)的距离。

至此就得到了完整的转子不平衡量预测模型,即通过圆柱度仪测试的跳动数据等计算获得在回转轴线坐标系下的单件静、偶不平衡量,整个转子装配体的静、偶不平衡量及质心分布情况。

2 不平衡量多目标优化

多级盘转子主要采用螺栓连接,上下连接件相对相位不同直接影响装配后的初始不平衡量。进行装配相位的多目标优化可以找到满足目标要求的最佳装配相位,实现装配后各个因素综合性能达到最佳,从而达到提高转子装配质量的目的。

2.1 优化目标

评价多级盘转子的装配质量的因素有很多,包括同心度、同轴度、不平衡量等,本文根据不平衡量预测模型选择3个优化目标,包括整体的静不平衡量和偶不平衡量的大小,还有各零件质心分布情况。三者都是影响装配质量的重要因素,这3个值越小装配后的转子质量越高,所以目标函数取它们的最小值,即:

(16)

式中:F1表示转子整体静不平衡量大小;F2表示转子整体偶不平衡量大小;F3表示质心分布情况;多级盘转子共有n级;xi表示第i+1级转子的安装相位;R=[R1,R2,…,Rn]T表示转子的基本数据包括质量、高度、转动惯量等;ε=[ε1,ε2,…,εn]T表示转子的跳动数据;函数f表示转子装配不平衡量预测模型的计算过程。

设计变量:多级盘转子由多个单件逐级堆叠而成的,每一级转子都有自己的安装相位,所以以第一级转子以外的单件装配相位为设计变量,设计变量的总个数取决于多级转子的级数。

x=[x1,x2,…,xn-1]T

(17)

式中n是转子总级数。

约束条件:由于多级盘转子主要由螺栓连接,所以装配相位主要由连接上下单件的螺栓孔数量限制,若多级盘转子第i级和第i+1级间的连接螺栓有mi个,则第i+1级的装配相位取值为

(18)

可以看出设计变量为离散型变量,是装配相位优化的主要约束条件。综上,得到的优化方程为:

(19)

2.2 优化方法

装配相位优化属于离散变量的求极值问题,优化算法有很多,这里选择一种效率较高且结果可以满足要求的一种多目标遗传算法(NSGA-Ⅱ),算法流程图如图6所示。

结果筛选:经过遗传算法NSGA-Ⅱ优化获得最终种群,由于3个优化目标没有明确的优劣关系,理论上最终的种群中所有值即为优化非劣解组(即没有任何一个个体的3个目标值均小于另一个),这里为了得到唯一确定优化结果,需要进一步的筛选,即进行优中选优。需要根据实际情况进行选择,本文的筛选函数设置为:

(20)

式中M表示结果中的中位数。

3 航空发动机高压转子算例

本文以某型航空发动机高压模拟转子(图7)为例,对转子装配不平衡量进行计算与优化。该模拟转子由前轴、一级盘、二级盘、三级盘、涡轮盘和后轴等6个单件组成,转子相邻两级盘间采用法兰盘连接、止口过盈配合定位、螺栓锁紧的结构形式。为更接近实际情况,这里假设整个转子上下两测量处径向跳动拟合圆圆心连线为整体回转轴线,即不平衡量计算及质心分布的基准轴线。

图7 高压模拟转子模型

3.1 高压转子装配不平衡量计算

首先通过测试的端面跳动、径向跳动数据及测量位置和测量半径等信息计算表示每个单件的4×4表征矩阵。经过堆叠装配,计算获得每个结合面处拟合圆心的位置;根据假设求回转轴线位置,即首末两圆心连线。再旋转装配体使Z轴与回转轴线重合,即在堆叠过程中,左乘矩阵M0。

(21)

进而计算获得各个单件装配后在回转轴线坐标系的质心坐标，如表1所示。

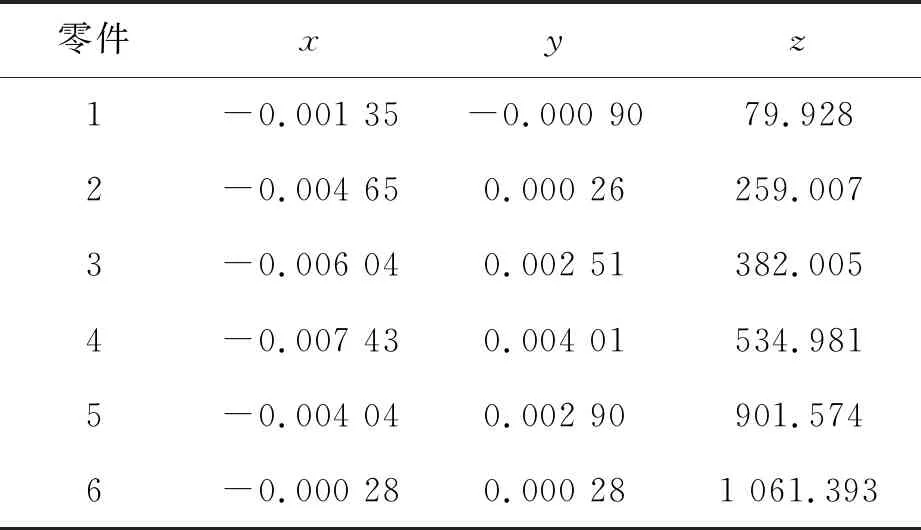
表1 质心位置

根据质心坐标及质量数据,计算得到静不平衡量，如表2所示。

表2 各单件静不平衡量

根据单件轴线与回转轴线的位置及转动惯量计算得到各单件装配后的偶不平衡量，如表3所示。

表3 各单件偶不平衡量

根据各个单件静、偶不平衡量,计算对于整个装配体的静、偶不平衡量，如表4所示。

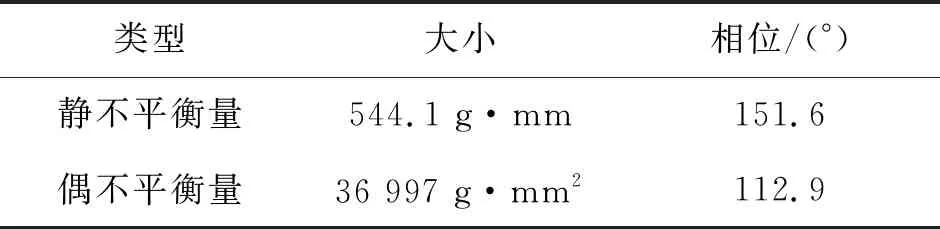
表4 整个装配体不平衡量

3.2 高压转子装配不平衡量多目标优化

利用Python geatpy工具包进行装配相位优化。种群规模200,算子变异概率0.1,算子交叉概率0.9,最大进化代数1 000。

得到的最终非劣解组如表5所示。

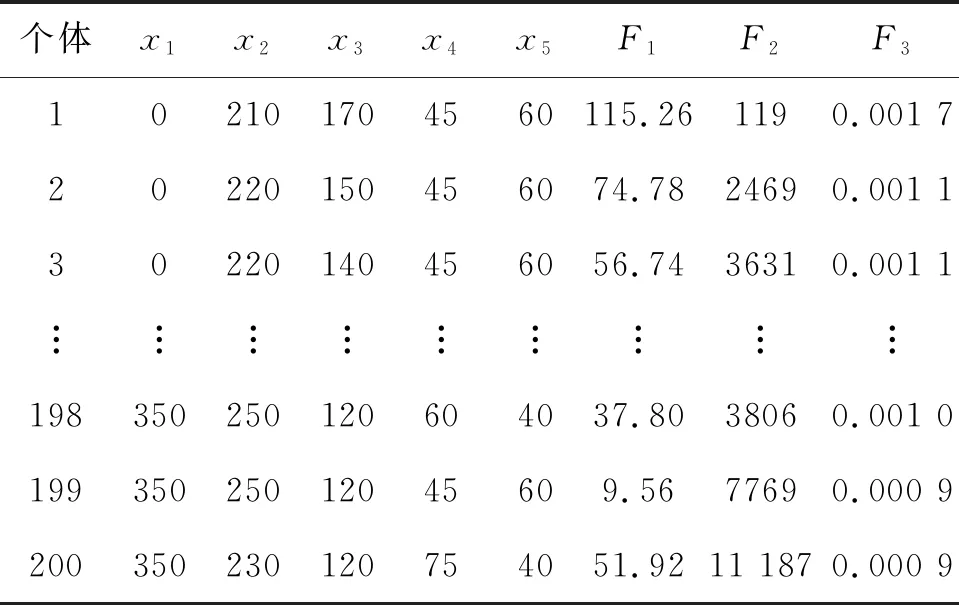
表5 非劣解组

其中x1、x2、x3、x4、x5为第2～6级转子单件的装配相位,x1、x2、x3有36个装配相位取,相邻位置相差10°;x4有24个装配相位,相邻位置相差15°;x5有18个装配相位,相邻位置相差20°;F1为装配后整体初始静不平衡量大小,g·mm;F2为初始偶不平衡量大小,g·mm2;F3为单件质心分布情况,mm。

经过结果评价选出来的最优结果如表6所示。

表6 优化结果

与初始相位装配和随机装配对比,结果如表7和图8所示。

表7 结果对比

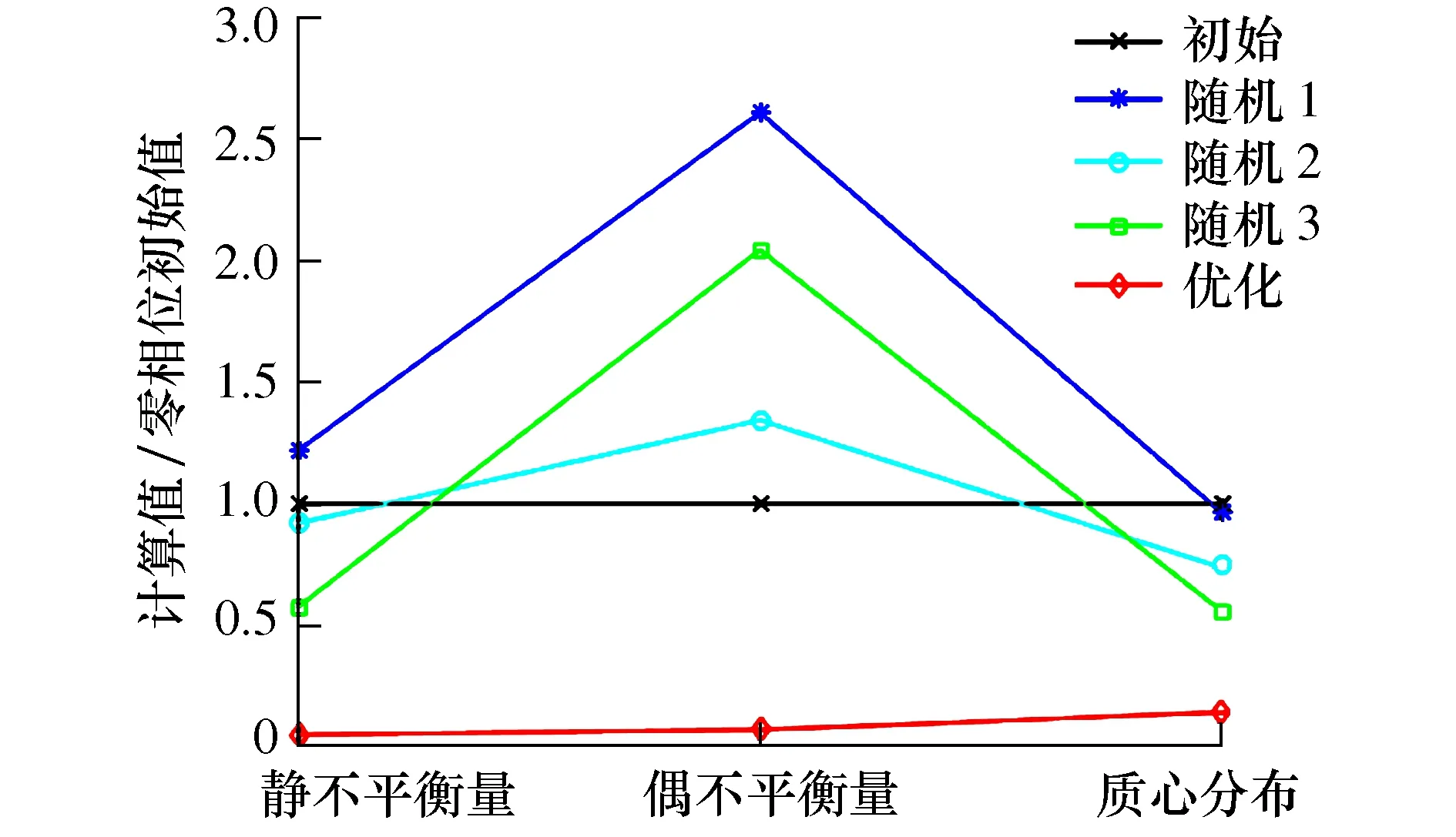
图8 结果对比

由表7和图8可知,优化方案对比初始和随机装配明显降低了装配之后的静不平衡量、偶不平衡量以及零件质心分布范围。其中对比初始状态静不平衡量降低至5.11%,偶不平衡量降低至7.09%,零件质心分布范围降低至14.29%,优化效果明显。

与不考虑质心分布的优化结果对比,结果如表8所示。

表8 两优化方法比较

两种优化方法的质心分布范围及延回转轴线投影对比，如图9所示。

图9 质心分布范围及延回转轴线投影对比

如图9所示,考虑质心分布优化对比未考虑质心分布的优化相比,前者能明显控制质心分布范围,但同时静、偶不平衡量也随之升高,工程实际中需要考虑具体情况选择合适的优化方法。若只关注装配不平衡量引起的振动,则不考虑质心分布;若考虑质心位置引起的零件结合面弯矩和发生变形后的不平衡量情况,则可以选择考虑质心分布的优化方法。

遗传算法优化结果与穷举法优化结果对比，如表9所示。