一种冗余机械臂的简化运动学求解方法
2022-08-30高春艳唐家豪吕晓玲张明路
高春艳,唐家豪,吕晓玲,张明路
(河北工业大学 机械工程学院,天津 300130)
冗余机械臂因其较好的避障和躲避奇异点的特性受到了学者们的广泛研究[1];但求逆解比较困难,目前,求逆解主要有3种方法:代数数值法、迭代算法和几何参数法。代数数值法主要有雅可比伪逆法[2-3]、二次规划反向算法[4];迭代算法主要有神经网络算法[5-6]、遗传算法[7-8]、粒子群算法[9-10]。魏延辉等采用了在求机械臂逆解中运用了构形平面几何参数方法,将机械臂三维问题转化为二维问题进行求解[11],但此方法对本次求解的机械臂不适用;韩书葵等采用代数法对机械臂进行计算[12],此方法主要同过联立方程对机械臂进行求逆解,易于理解但计算较为复杂;王鹏程等提出了“自由度模块化”的概念,通过将复杂的空间机构运动学问题转变为平面机构问题,大大提高了计算速度[13],但对此机械臂不适应;刘世平等采用BP神经网络对机械臂进行求解,主要通过神经网络的训练数据拟合来实现各关节角度的反解[14];此方法需要进行训练数据,故对求解速度有所影响;胡奎等针对关节限位的机械臂求出了逆解[15]。上述几种求逆解的方法,有的因其求解过程复杂,影响计算效率,有的不适用于此机械臂。
本文针对一种S-R-S构形的机械臂,在建立机械正运动学模型的基础上,提出了一种几何法和代数法相结合的冗余自由度求逆解的方法,此方法形式简单,能够快速得到所需关节转角。
1 机械臂正解
首先根据机械臂模型采用D-H法对机械臂进行建模,机械臂模型如图1所示。

图1 机械臂实体模型图
根据机械臂模型得到机械臂参数如表1所示。

表1 机械臂D-H参数表
机械臂正向运动学中,根据D-H参数模型可以得到两个相邻坐标系之间的转换关系为

(1)
式中:Rot(z,θi)为坐标系绕z轴的旋转矩阵;Trans(z,di)为坐标轴沿z轴平移矩阵;Trans(x,ai)为坐标轴沿x轴平移矩阵;Rot(x,αi)为坐标系绕x轴的旋转矩阵。
根据计算可得
(2)
将机械臂参数表中的参数代入式(2),并令cosθi=ci、sinθi=si可以得到:
(3)
(4)
(5)
(6)
(7)
(8)
求得正解为
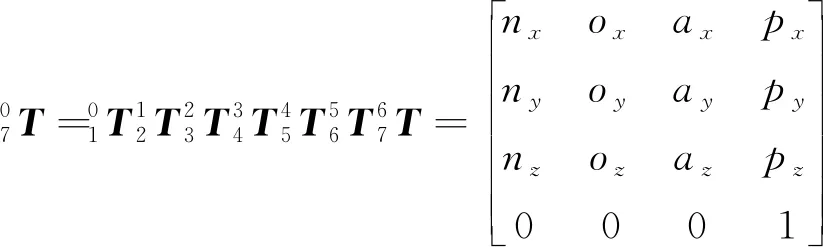
(9)
2 机械臂逆解

图2 自运动示意图
2.1 θ4的求解
为求解θ4将机械臂模型简化,如图3所示。
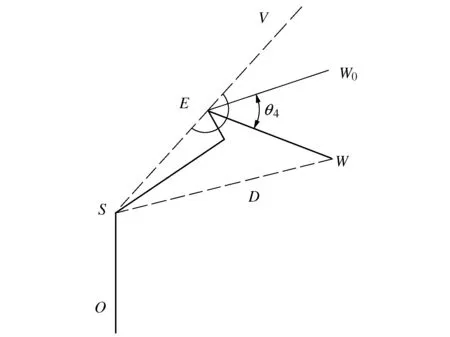
图3 θ4求解示意图
在图3中,S点的坐标为(0 0d1),W的坐标为末端位置坐标,为(pxpypz)。
由图3可知:
(10)
∠SEW0=2arctan(lED/lSD)
(11)

根据几何关系可得θ4=∠SEW0-∠SEW。
2.2 臂型角θ0=0时,θ1、θ2、θ3的求解
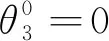
(12)
又根据几何关系,坐标轴3中的y轴在基坐标系下的投影为
(13)
根据旋转矩阵的定义,可得
(14)
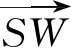
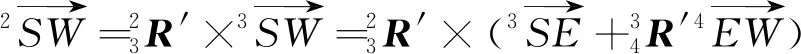
(15)

(16)
(17)

2.3 求解θ1、θ2、θ3
根据Rodrigues 公式可得

(18)

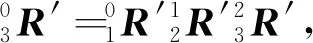
(19)
根据D-H坐标变换有
(20)
将式(19)与(20)联立,即可求得:

(21)
2.4 求解其他关节转角
其中θ5、θ6和θ7可通过下式求得
(22)
等式左边已知,等式右边根据D-H参数可得
(23)
联立式(22)和(23),即可求得
(24)
至此,求出所有关节转角。
3 仿真
使用MATLAB中的Robotics Toolbox进行仿真,根据上文所述方法,在MATLAB中进行编程,首先随机给定50组角度进行求正解,根据正解得到的位姿矩阵进行求逆,将求得的逆解再次代入正解矩阵求得位姿矩阵,将所给位姿与求得位姿对比,得到误差如图4所示。
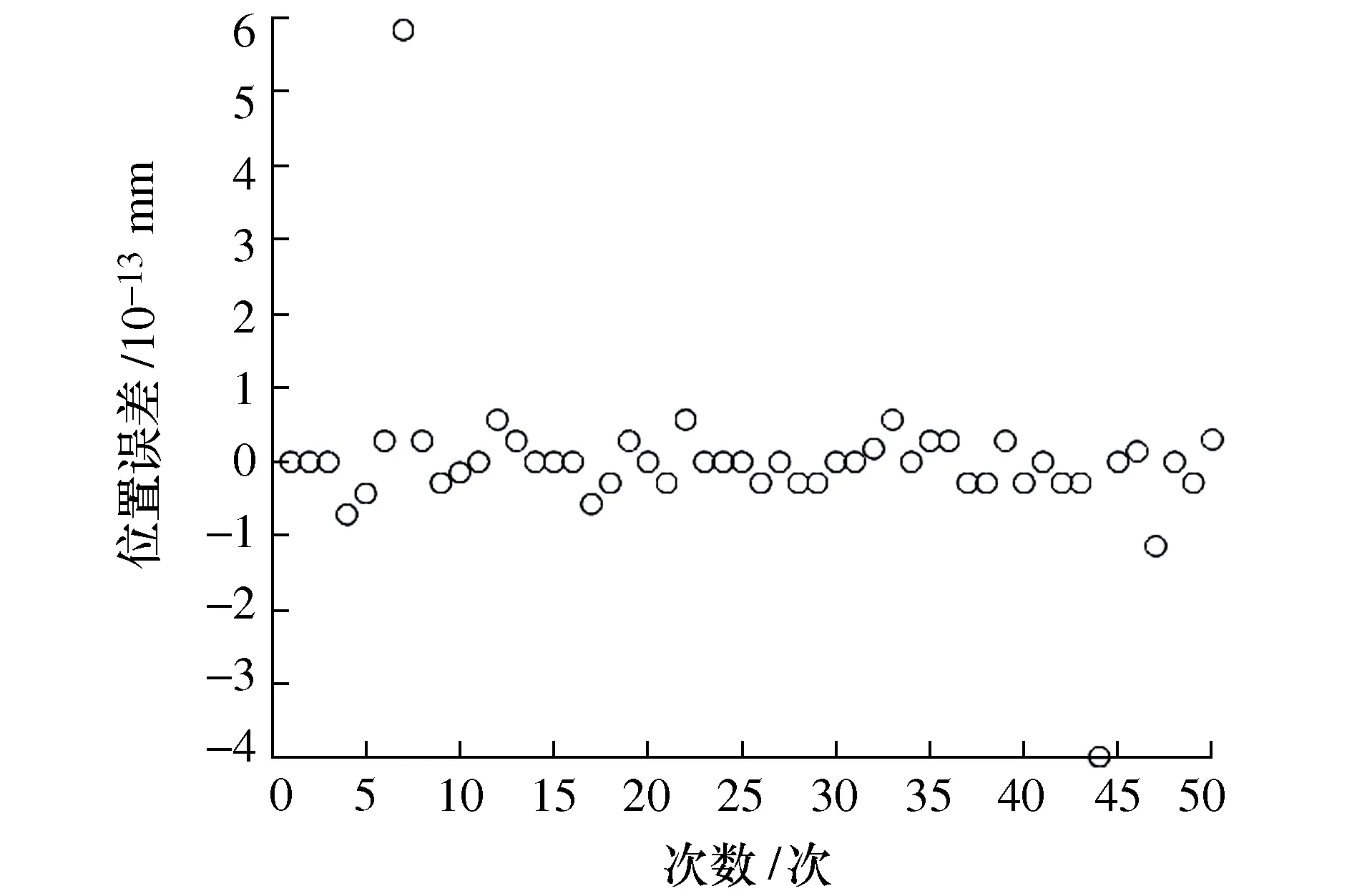
图4 位置误差图
由图4可知,位置误差最大不超过6×10-13mm,故满足其精度要求。
从随机的50组数据中再挑出3组进行验证,第一组数据为
(25)

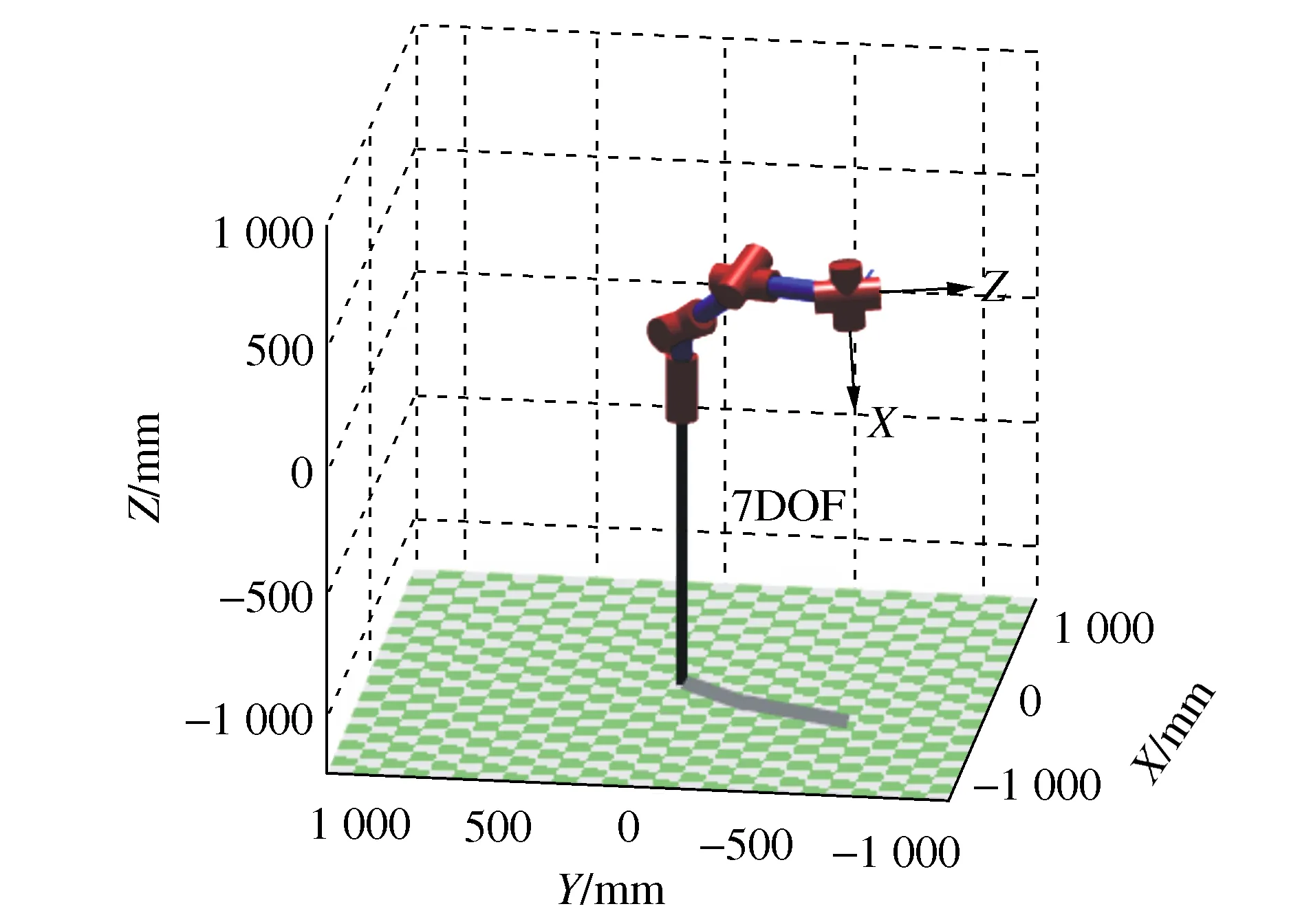
图5 第一组数据姿态
第二组数据为
(26)


图6 第二组仿真位姿
第三组数据为
(27)
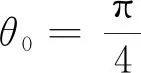

图7 θ0分别取0和机械臂位姿
通过上述实验计算逆解,并观察逆解计算时间,发现此逆解算法耗时0.50 ms。之后,对机械臂的逆解进行运动仿真,随机给定机械臂初始位姿和目标位姿,并在其中插值50次,机械臂从初始位姿运动到末端位姿每个关节角度随时间变化如图8所示,机械臂末端位置变化如图9所示。通过此仿真可以看出此逆解方法得到的轨迹顺滑,并且仿真结果正确,因此求逆解的方法正确有效。

图8 各关节角度随时间变化图
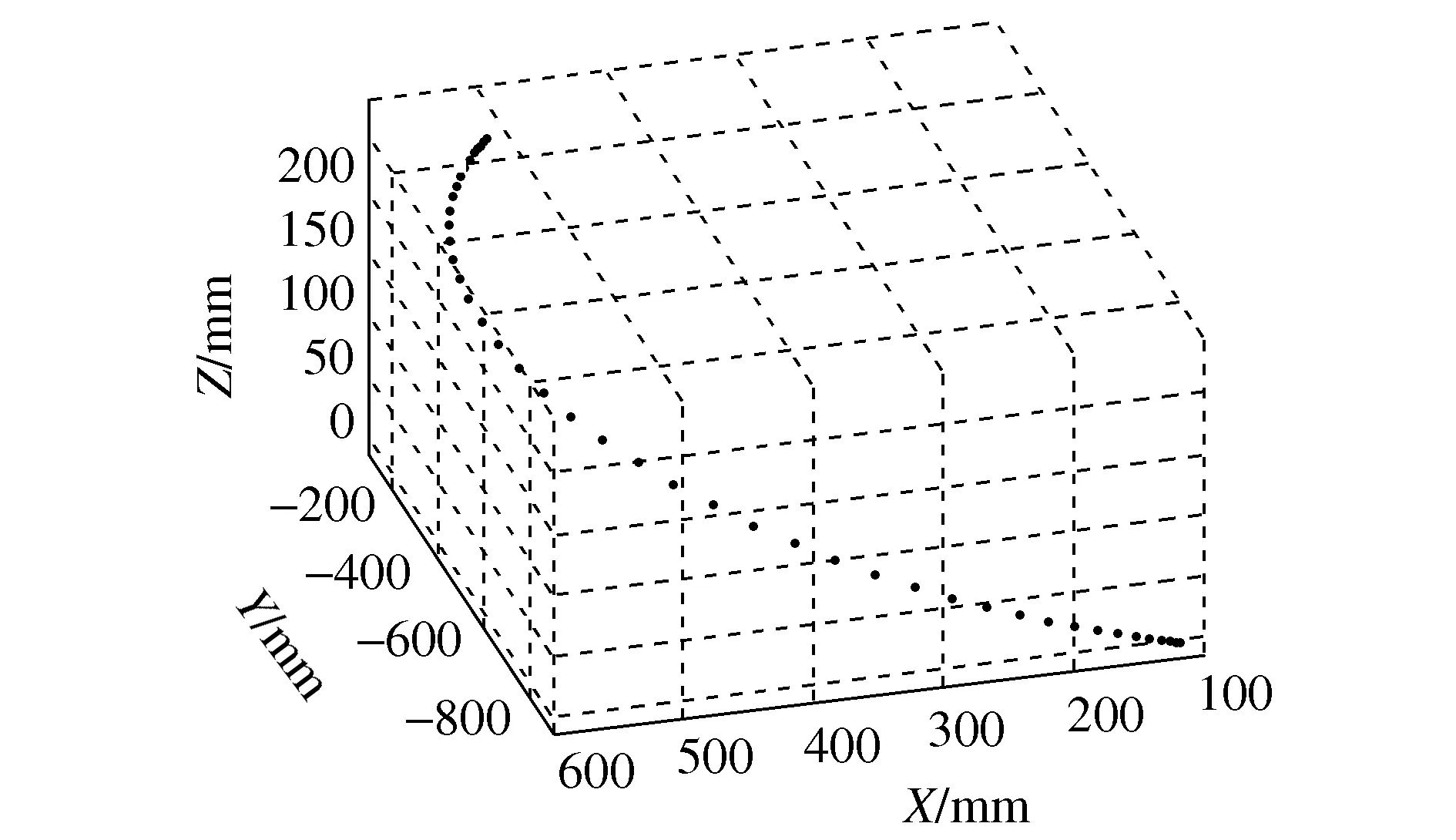
图9 机械臂末端变化图
4 结束语
本文针对一种特殊机械臂对其进行了运动学分析,提出了一种几何法和解析法相结合的求逆解方法,并对这种方法进行了仿真实验,实验结果表明此方法具有高精度,运算简单的优点,对之后的运动学控制和路径规划具有较好的实用价值。
