焊锡机器人关节空间最优路径规划方法研究
2022-08-30赖俊豪朱大昌朱厚耀曾俊海杨家谋杜宝林
赖俊豪,朱大昌,朱厚耀,曾俊海,杨家谋,杜宝林
(广州大学 机械与电气工程学院,广州 510006)
20世纪70年代以来,焊接机器人已被广泛用于汽车、摩托车、工程机械制造业。其中点焊机器人占比约为45%,并大量用于汽车白车身,PCB板,家电五金等焊接工况[1]。合理的机器人焊接路径规划对减少生产节拍时间、提高机器人运行的平稳性和寿命以及提高汽车的更新换代效率有着很大的意义[2]。例如,大型构件(大尺寸PCB板)焊接中,存在焊点数量繁多、空间分布错综复杂、焊接工艺要求严格等因素,则需要对焊接路径进行合理规划,提高焊接效率。候仰强等[3]基于蚁群粒子群混合算法,建立白车身侧点焊多机器人协调焊接数学模型,实现了焊点的均匀分配和单机器人焊接路径最优。刘海江等[4]通过对白车身多机器人工位焊点任务分配问题进行了数学分析,建立多背包问题模型,并基于遗传算法设计出求解该问题的方法。姚江玉等[5]针对焊接过程中焊枪的避障问题,提出了基于改进人工蜂群算法的机器人避障焊接路径规划策略。陈立等[6]针对基本蚁群算法在焊锡机器人路径优化存在交叉点的不足,提出一种自动消除焊接路径中交叉点的算法,将其与蚁群算法融合,通过增加消除交叉环节,得到更优的焊接路径。传统点焊路径规划模型是以焊点在笛卡尔坐标下的最短距离作为路径最优评价标准[7-8],但该路径规划方法往往不能同时实现机器人能量损耗最小和加工时间最优。本文以3-RRR并联焊锡机为研究对象,建立其正逆运动学方程及基于关节空间角度加权和的路径规划数学模型,并设计了一种带有精英策略和信息挥发自适应调节函数的改进蚁群算法对路径规划模型进行优化。通过焊锡工况仿真实例与传统笛卡尔坐标下的路径规划进行比较分析,实验数据表明,用关节空间路径规划模型优化的锡焊机器人路径总关节空间角度加权值更小,进而验证了所提出路径规划方法在缩减焊接机器人能量损耗和加工时间方面的有效性。
1 3-RRR并联焊锡机的运动学建模
1.1 3-RRR并联焊锡机模型
本文以3-RRR并联焊锡机作为研究对象,该焊锡机主要由动平台、焊头、定平台、电机驱动杆及从动杆等部分组成,其三维模型如图1所示。焊锡机的连杆之间、杆件与动定平台之间均通过R副连接。
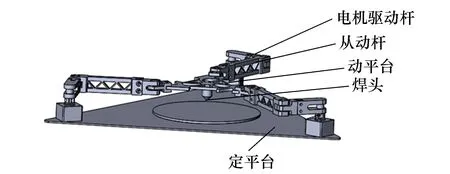
图1 3-RRR并联焊锡机三维模型
1.2 3-RRR并联焊锡机的逆运动学方程
3-RRR并联焊锡机的结构简图如图2所示,其动、定平台均为等边三角形,动平台与各支链的连接点分别为C1、C2、C3,定平台的3个连接点分别为A1、A2、A3,B1、B2、B3为驱动杆与从动杆的连接点。
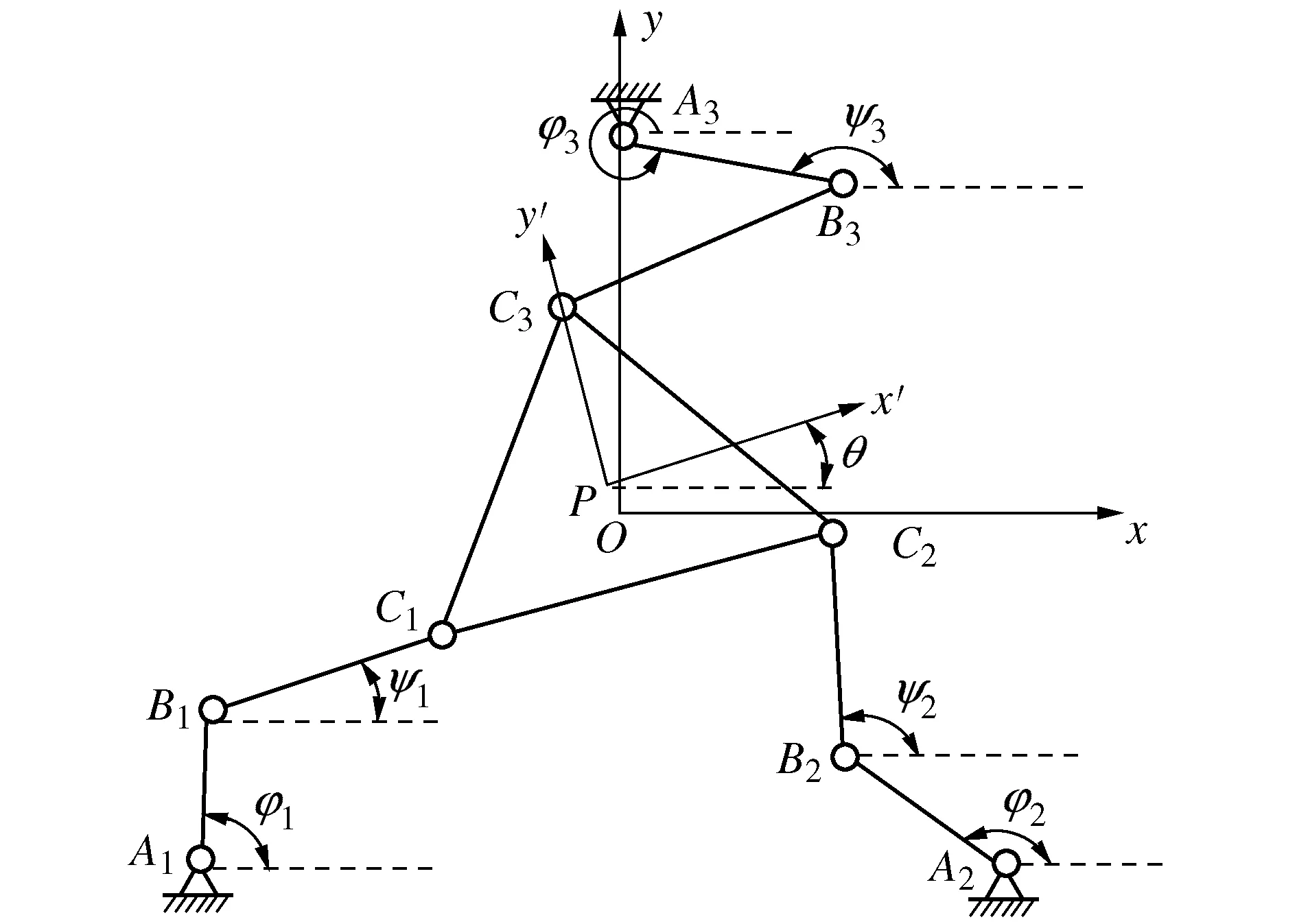
图2 3-RRR并联焊锡机简化模型


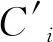
(1)

(2)
设运动平台中心点的位移为(xp,yp,θ),联立式(1)、式(2)求出3-RRR并联焊锡机3个驱动杆所转过的角度(φ1,φ2,φ3),即运动学逆解为:
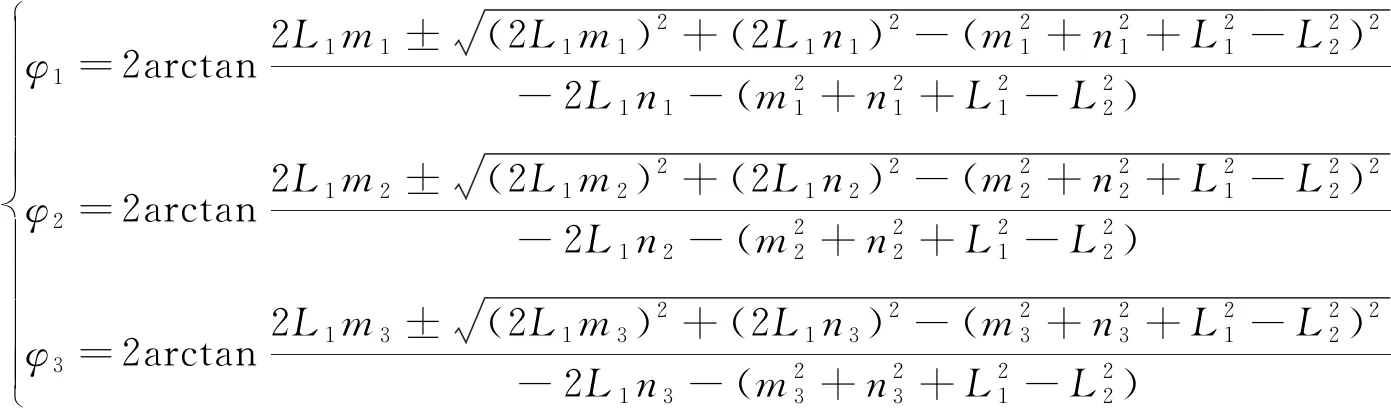
(3)
其中:
1.3 3-RRR并联焊锡机的正运动学方程
用(xc1,yc1)表示C1的全局坐标,(Bix,Biy)(i=1,2,3)表示B1,B2,B3的全局坐标位置,联立式(1)和式(2)得出方程组如下:
(4)
方程组(4)可以化简成的矩阵形式为
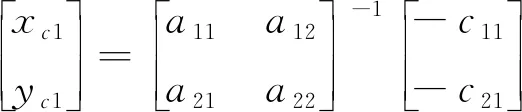
(5)
其中:
a11=2bcosθ-2B2x+2B1x
a12=2bsinθ-2B2y+2B1y


(6)
2 最优路径规划
2.1 最优路径规划数学模型
焊接机器人在焊点之间的控制属于点位控制,只需考虑邻近加工焊点间的始末加工姿态[9]。传统点焊路径规划是以焊点在笛卡尔坐标下的最短距离作为最优评价标准,但该方法往往不能同时实现机器人能量损耗最小和时间最优。而以时间-能量消耗作为优化目标的函数通常要结合动力学模型进行求解,计算量则十分庞大[10]。基于此,本文提出一种基于关节空间角度加权和的最优路径规划方法。
根据机器人动力学和点到点之间的轨迹规划方程,可以得到机器人系统的整体时间-能耗模型如式(4)所示[11]。为简化计算,把该模型转化成单关节的时间-能耗模型,即

(7)
式中:dθi为关节角位移;tf代表轨迹的总运行时间;弹性系数ηi让总时间和单关节能耗处于同一数量级;ki1、ki2为权衡系数,ki1+ki2=1;n表示机器人系统的关节数量;τi表示第i个关节的力矩值,i=1,2,…,n。整体时间-能耗函数可以写为
Z=z1+z2+…+zn
(8)
设点与点之间的轨迹规划均采用五次多项式规划,且初始点位的角速度,角加速度都为零。不考虑关节摩擦和电机热量耗损,以单关节为分析对象,当关节角度变化越大,轨迹规划时间越长且单关节能耗越大。单个关节的角度变化值与轨迹规划时间和关节能耗值呈正相关,进而推出zi与dθi呈正相关。
设S={s1,s2,s3,…,sn}是n个所需加工焊点对应角度变化的集合,机器人系统的驱动关节为k个,则S可以写成

(9)
用Hij(i,j=1,2,…,n,且i≠j)表示任意两个焊点之间带权值的各关节空间角度变化绝对值之和,则对Z的优化可以转化成对Hij的优化,其表达式为
Hij=w1|si1-sj1|+w2|si2-sj2|+…+wk|sik-sjk|
(10)
w1~wk为对应各关节时间-能耗模型的权重因子,表明相同角度变化下各关节时间-能耗函数值zi之间的权重。权值根据zi之间的大小来进行调节,使Z值的优化等效成Hij的优化。为了让机器人加工时间更短和能耗最小,则应规划出加工焊点的最优次序使得总加工路径的关节空间角度加权和最小。
2.2 蚁群算法的改进
蚁群算法是通过模拟自然界中蚂蚁对“信息素”的感知能力来寻找最优觅食路径的一种群智能优化算法[12]。针对传统蚁群算法易早熟、搜索路径效率低及收敛速度慢等缺陷[13],本文利用精英策略强化精英蚂蚁[14-15]对信息素浓度的影响,并对信息挥发因子进行自适应调节,以增强蚁群算法收敛速度和全局搜索能力。设计的改进蚁群算法流程图如图3所示。
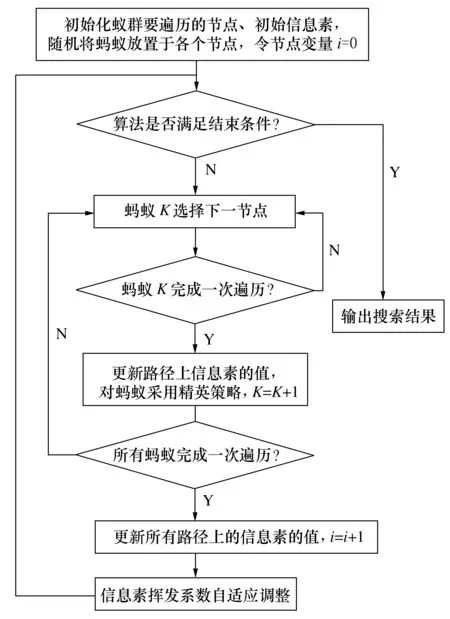
图3 改进蚁群算法流程图
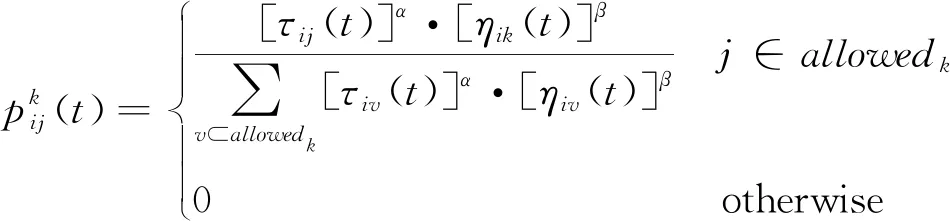
(11)
式中:allowedk表示蚂蚁k下一步允许选的焊点位置;τij(t)为t时刻路径(i,j)上的信息量;α为信息启发式因子;β为期望启发式因子;ηik(t)为启发函数,这里取关节空间角度加权和的倒数,其表达式为
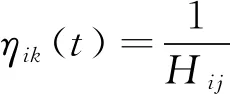
(12)
信息素浓度规则为:
τij(t+n)=(1-ρ)·τij(t)+Δτij(t)
(13)


(14)
式中:λ=e(1-Lk/Lbest),Lk为当前所有蚂蚁走过的最优路径;Lbest为历史迭代中蚂蚁走过的最优路径;Q为信息素强度。当Lk>Lbest时则削弱当前蚂蚁对信息素浓度的影响,当Lk 信息素挥发系数对蚁群算法的收敛速度和全局搜索性能有着直接的影响,当ρ过大时,会加大路径重复选择的可能性,当ρ过小时,可以提高算法的随机性和全局性,但收敛速度会变慢,根据ρ的特性设计自适应调节函数为 (15) 式中:N为当前迭代次数;Nmax为最大迭代次数。自适应调节函数的作用主要是在算法前期加大蚂蚁的搜索能力,防止过早局部收敛,中后期衰减信息挥发因子,防止无效的路径过渡搜索,增强算法的收敛速度。 表1 焊点位置点及对应的关节空间角度值 设基于关节空间的路径规划函数的权值w1=w2=w3=1,该改进蚁群算法的信息素强度Q为10,信息素初始浓度为1,蚂蚁的总数为m=30,信息启发因子α=1,期望启发因子为β=5,最大迭代次数为200,改进蚁群算法的ρ的初始值设为0.5,ρmin设为0.2。对该3-RRR并联焊锡机焊锡工况进行加工路径规划,基于关节空间角度加权和的改进优群算法的迭代曲线和最优焊点路径如图4和图5所示。 图4 基于关节空间角度加权和的迭代曲线 图5 基于关节空间角度加权和的最优路径 与传统笛卡尔坐标下的最优路径规划仿真数据进行比较分析,结果如表2所示。结果显示,在关节空间路径规划下,3-RRR并联焊锡机完成所有焊点加工的总角度加权值为158.68°,其加工路径在笛卡尔坐标的总距离为473.64 mm。基于笛卡尔坐标最优路径规划的总路径距离比前者少42.89 mm,其关节空间角度加权和为176.26°,比前者多17.58°。 表2 关节空间和传统笛卡尔空间路径规划比较 在本文中,针对焊接机器人点焊工况,提出一种基于关节空间角度变化加权和的最优路径规划数学模型,并设计了一种带有精英策略和信息挥发因子自适应调节函数的改进蚁群算法对所提规划方法进行优化,最后以3-RRR并联焊锡机的焊锡工况为例,利用改进的蚁群算法进行关节空间角度加权和的最优路径规划。仿真数据表明,与传统的笛卡尔坐标最优路径规划相比,基于关节空间角度变化加权和的最优路径规划缩短了总关节角度加权值17.58°,验证了该数学模型在减少焊锡机器人的加工时间及能量损耗方面的有效性,对提高传统焊接机器人的加工效率有着一定的参考价值。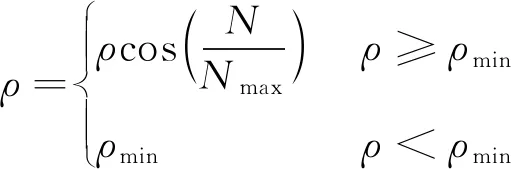
3 最优路径规划




4 结论
