不均匀坝基条件下混凝土拱坝失效模式分析

刘 杰，荆帅召

(1.重庆市水利电力建筑勘测设计研究院有限公司，重庆 400020；2.河海大学水利水电学院，江苏 南京 210098)

近些年来，拱坝由于其安全和经济方面的优越性，已成为大坝设计中的三大优选坝型之一[1- 3]。随着我国水利事业的不断发展，在西部地区已修建了许多超过200m的拱坝，如小湾、溪洛渡、锦屏、白鹤滩等[4- 5]。而坝基岩体的不均匀性作为一种常见的地质缺陷，往往会引起拱坝的失稳破坏，造成十分严重的后果[6- 7]。因此，研究不均匀坝基条件下坝体的破坏与失稳机制对于保障拱坝的安全运行具有重要意义。

有限元法由于在处理复杂边界及荷载条件、复杂结构和非线性问题方面具有独特的优势，广泛应用于水工结构破坏分析中[8- 11]。而对于水工混凝土这种复合材料，由于其抗拉强度较低，在模拟混凝土损伤破坏时常会导致结构出现刚度矩阵的不对称现象，这使得基于隐式算法的有限元分析易出现不收敛的问题。同时，多数隐式分析需通过反复调整模型参数来避免计算出现不收敛，易引起较大的计算误差，且试算过程需消耗大量时间。而显式有限元方法基于动态算法则无需迭代计算，对于高度非线性问题不存在收敛困难，同时能够较为真实地模拟结构的实际加载过程[12]。另一方面，通用有限元软件ABAQUS以其强大的非线性求解能力而被广泛应用于水工结构仿真计算中[13]，其基于显式算法开发的显式分析模块ABAQUS/Explicit对于求解各类非线性结构力学问题非常有效[14]。

鉴于此，本文基于三维非线性显式有限元方法，利用ABAQUS对位于不均匀坝基上的某混凝土拱坝进行数值模拟分析，总结出坝基岩体的非均匀性对混凝土拱坝损伤破坏过程和失效模式的影响，可为拱坝结构的整体优化设计和确定坝基岩体工程加固方案提供技术参考。

1 基于ABAQUS的非线性有限元显式分析方法

ABAQUS/Explicit中的显式分析方法采用时间差分法进行积分[15]，通过上一个增量步的动力计算条件进行计算并获取后一个增量步的动力计算条件，不必再进行平衡迭代，因此计算速度快，一般不会出现计算不收敛问题。具体求解步骤如下：

增量步开始，程序首先求解动力学平衡方程，节点合力的求解方程为：

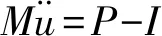
(1)

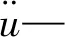
增量步开始时(t时刻)，计算加速度为：

(2)

采用中心差分法计算加速度对时间的积分，计算速度变化的过程中假设加速度为常数，则当前增量步中心点速度的计算公式为：

(3)

当前增量步结束时的位移计算公式为：

(4)

不同于隐式分析的无条件稳定，显式分析作为一种条件稳定算法，要求时间增量步长Δt不能大于稳定时间步长限制值Δtstable，即Δt≤Δtstable，否则会导致结构响应出现波动，计算结果出现无边界的振荡发散。无阻尼时，Δtstable可由下式估计：

(5)

式中，ωmax—模型最高固有频率；Le—最小尺寸单元的长度；cd—材料波速，可由材料的弹性模量、泊松比和密度决定。

2 不均匀坝基拱坝损伤破坏分析

2.1 工程概况

为研究不均匀坝基条件下混凝土拱坝失效模式，本文以我国西南部某水平拱圈呈抛物线型的混凝土双曲拱坝作为研究对象进行显式有限元分析。

该拱坝最大坝高78m，最低建基面高程441m。坝肩地质断面及开挖线如图1所示，坝基由多个不同厚度的水平岩层组成。根据地质勘查资料，441～480m高程的下部坝基岩层的力学性能明显强于480m高程以上的上部坝基岩层，坝基岩体整体处于不均匀状态。

图1 坝肩地质断面图

2.2 有限元计算模型及荷载工况

本文采用ABAQUS/Explicit计算混凝土拱坝坝体-坝基的三维有限元计算模型。拱坝与坝基系统整体有限元网格主要由八节点六面体单元组成，结点和单元数分别为154813和141877，如图2(a)所示。为更真实地模拟拱坝坝体损伤破坏的发生位置和扩展过程，对坝体模型进行了较为精细的网格离散。坝体部分的最小单元尺寸为1.5m，结点和单元数分别为24660和21064，图2(b)所示。

此外，本文采用水密度超载法[16]开展超载工况分析，可间接模拟由于材料强度降低导致大坝失效的过程，具体介绍如下：假定六组超载系数，超载系数为施加的水荷载与正常荷载的比值，即将上游水容重增加到正常工况下的1、2、3、4、5、6倍，分别试算拱坝超载1～6倍水压荷载，分析得到超载系数下相应的应力位移分布情况及塑性破坏区域。

图2 拱坝三维有限元模型

2.3 材料本构模型及力学参数

坝体混凝土材料在拉压过程中因塑性积累和刚度的退化，性能变化极其复杂。而混凝土连续损伤塑性模型(CDP)[17]作为一种典型的非线性损伤模型，考虑了混凝土材料拉压性能的差异，可较好地模拟混凝土材料在外荷载作用下由于损伤引起的刚度退化。因此，为了能较好地描述混凝土材料的力学特性，本文采用ABABUS内置的CDP模型作为坝体混凝土材料的本构模型，其他相关混凝土力学性能参数见表1。

表1 混凝土材料力学性能参数

对于坝基岩体，本文采用ABAQUS软件提供的线性Drucker-Prager模型[18- 19]作为本构模型，其考虑了中间主应力和静水压力的影响，可较为准确地描述坝基岩体的力学特性。同时，为体现坝基岩体的不均匀性，力学性能相对较好的坝基岩体采用实际的力学参数，而对于力学性能较差的坝基岩体则采用参数折减法描述其力学性能。上部软弱坝基岩体力学参数为折减系数与下部坝基岩体力学参数的乘积，其中软弱坝基岩体密度与泊松比的值保持不变。折减系数值R分别取为1.0、0.7、0.5、0.3，不同R值对应的软弱坝基岩体的力学参数见表2。

表2 坝基岩体力学性能参数

2.4 结构准静态模拟分析

为解决显式算法分析的条件稳定性问题，需对拱坝坝体-坝基系统模型进行准静态模拟分析，将结构响应引起的波动性控制在工程可接收的范围内。而满足显式计算准静态分析要求的主要因素和要点包括加载幅值曲线、加载时长以及模型的网格划分3个方面。

由于显式分析是基于自然时间的求解过程，且由式(5)可知时间增量Δt数值上非常小，因此模型加载时长若取值过小会引起动态效应造成计算误差，过大则会提高计算的时间成本。而另一方面，在结构准静态加载过程中，最小自振周期对结构的响应具有控制性作用。因此，可将模型加载时长增加到系统最小自振周期的10倍左右[20]，以减小荷载施加过快引起的动态效应，使计算结果的准确度和计算效率满足要求。经过计算，拱坝坝体-坝基系统结构的最小自振周期为0.796s，综合考虑，取加载时长为20s。

其次，在模型加载过程中，若加载速度出现突变，则会引起结构的震荡，造成计算结果出现较大偏差[21]。因此，为使准静态分析结果的误差更小、计算效率更高，本文ABAQUS中选用如图3所示加载过程平滑、波动性较小的光滑函数曲线。该曲线将两个自定义的幅值间以五阶多项式进行过渡，在自定义的幅值点处速度和加速度为0。

此外，由于最小网格尺寸与数值模拟的精度成反比，且由式(5)可知，稳定极限大致与最短的单元尺寸成比例，因此最小单元尺寸的合理选取对显式计算结果影响重大，且结构网格的划分应尽量均匀。本文限于篇幅和计算量，只选取一种较为合理的网格划分方式。

由于实现准静态分析的核心要求是选择合理的加载速度，为判断上述方法是否满足准静态分析要求，本文以加载过程中结构的动能与内能的比值不超过10%作为判断准则[22]。其中，动能表征结构运动速度，内能表征结构变形程度。

图3 平滑幅值曲线

3 结果分析

3.1 准静态分析验证

由2.4节可知，在ABAQUS后处理中可绘制结构动能与内能的比值随时间变化的曲线用于检验结构在运算过程中是否处于准静态。本次分析结果如图4所示，结构动能与内能的比值在整个加载过程中的最大值仅为0.0113%，满足准静态分析要求。

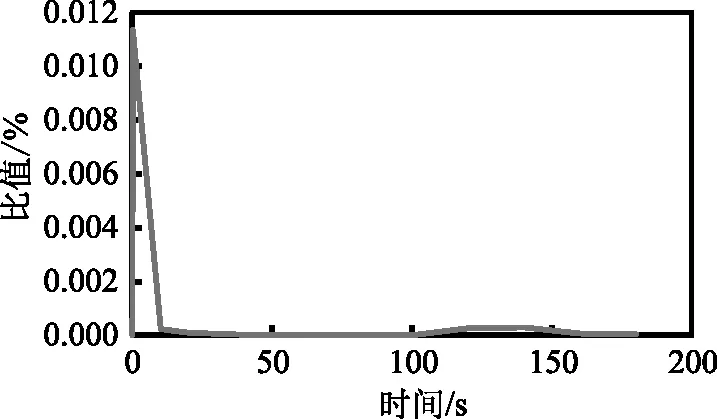
图4 动能/内能随时间变化值

3.2 超载破坏分析结果

超载分析中，本文以塑性区贯通作为拱坝结构完全破坏的标志，以等效塑性应变超过100με作为混凝土材料进入塑性的指标[23]。针对不同R值下的坝基条件，图5—8分别展示了塑性区贯通时相应超载倍数下拱坝的塑性区(红色区域)分布。

(1)当R=1.0时，坝基岩体可视为均匀岩体，超载倍数达到6时坝体塑性区贯通，如图5所示，拱坝的塑性区主要集中在拱坝坝体底部、上游面拱端处、下游面上部拱端和靠近坝顶的中心区域。

图5 折减系数R=1.0，超载倍数6.0

(2)当R=0.7时，超载倍数达到4.5时坝体塑性破坏区贯通，如图6所示，且与R=1.0时拱坝上下游面塑性破坏区分布位置基本一致。

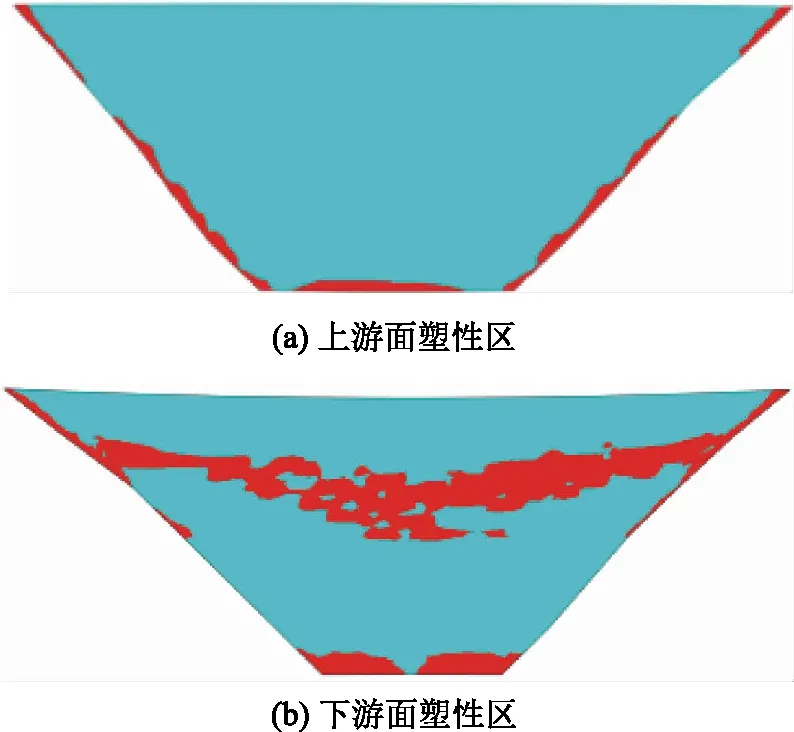
图6 折减系数R=0.7，超载倍数4.5

(3)当R=0.5时，拱坝在超载倍数为3.5时塑性区贯通，如图7所示，相比于R≥0.7时，上游面塑性区在480m高程以上分布有所增加，而其他塑性区分布位置基本保持不变；下游面塑性破坏区在480m高程处从拱端向中心区域发展，但仍未贯通，而靠近坝顶中心区域的塑性区减少。

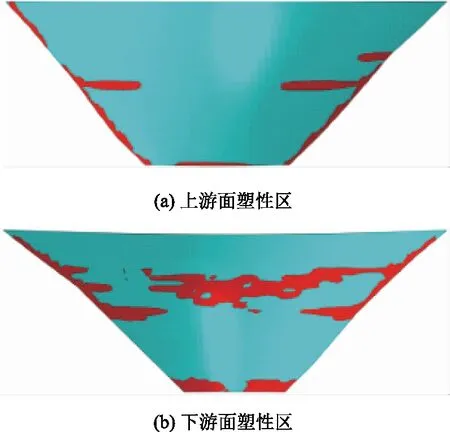
图7 折减系数R=0.5，超载倍数3.5

(4)当R=0.3时，拱坝在超载倍数达到2.5倍后塑性破坏区贯通，如图8所示，上下游塑性破坏区皆贯通于480m高程拱圈附近区域。上游面底部由于中心区域的屈服破坏使得梁的作用失效，并未出现塑性屈服。

图8 折减系数R=0.3，超载倍数2.5

3.3 失稳模式分析

(1)失效模式Ⅰ：当R≥0.7时，坝基岩体不均匀程度较低，塑性区分布位置随R值的改变并无显著变化，这意味着下部坝基岩体对拱坝的失效模式影响更大。此种损伤破坏模式可定义为失效模式Ⅰ。在失效模式Ⅰ下，拱坝的损伤破坏主要受到坝体与下部坝基之间相互作用的影响。

(2)失效模式Ⅱ：相较于R≥0.7的情况，R=0.5时，在480m高程拱端附近也出现了塑性区，此时坝基岩体的不均匀程度对拱坝破坏机制产生了一定影响，此种损伤破坏模式可定义为失效模式Ⅱ。对于失效模式Ⅱ，拱坝的失稳破坏主要受到坝体与上部和下部坝基共同作用的影响。

(3)失效模式Ⅲ：当R=0.3时，坝基岩体不均匀程度较高，拱坝的塑性区主要集中在480m高程处对应的拱圈附近区域。相较于失效模式Ⅰ，拱坝的破坏位置和形式发生了明显变化，此种损伤破坏模式可定义为失效模式Ⅲ。对于失效模式Ⅲ，拱坝的失稳破坏主要受到坝体与上部坝基之间相互作用的影响。

4 结语

为研究不均匀坝基条件下混凝土拱坝的失效模式，基于实际工程对位于不均匀坝基上的混凝土拱坝开展了一系列的数值计算，主要结论如下：

(1)基于显示有限元的准静态分析方法得到混凝土拱坝失效的全过程。

(2)受坝基不均匀程度的影响，混凝土拱坝存在3种失效模式。

(3)对于不同的失效模式，提出了当折减系数值R达到一定数值后，一般性的工程措施很难满足大坝安全需要，其余可根据混凝土的失效过程对坝基采用相对应的加固措施，可为后续类似工程设计提供技术参考，具有较为重要的学术意义与工程应用价值。