茨淮新河灌区中长期供水优化调度建模与分析
2022-08-29李杰
李 杰
(安徽省水利水电勘测设计研究总院有限公司,安徽 合肥 230088)
1 研究背景
茨淮新河灌区位于黄淮海平原南端,地处南北方气候过渡带,水热资源优于北方,光资源优于南方,但旱涝灾害频繁,年内常有旱涝交替的现象发生。灌区承担防洪、排涝、供水、生态、航运等多种调控任务,运行调度涉及多目标和多制约因素,条件复杂[1]。解决新时代灌区面临的问题,就必须突破传统的治水思路,依靠信息科技进步,通过加强水利信息化建设,推进水利的现代化[2- 4]。因此,开展茨淮新河灌区联合优化调度方案的编制工作,能够科学地规划和利用灌区内可用水源,抓好调水、输水、灌水、用水、排水过程,为防汛抗旱调度和水资源配置调度提供科学的决策支撑。
灌区各级枢纽联合优化调度是发挥水利枢纽工程综合效益的关键,也是目前水利科学技术人员关注和研究的热点问题[5- 7]。经过多年的研究发展,灌区调度模型及其高效求解方法理论研究已积累了丰硕的成果,广大学者在探索和认识梯级枢纽优化运行规律方面做出了杰出的贡献。线性模型[8]、非线性模型[9]、随机模型[10]和多目标优化模型[11- 12]相继提出并运用于联合优化调度方案编制,相比于前几种模型,多目标优化模型能同时优化多个目标,权衡各个目标间的竞争冲突关系,通过单次计算即可得到一组非劣方案集,计算效率较高。在过去的几十年中,出现了各种多目标进化算法,例如基于非支配排序遗传算法(NSGAII)[13]、基于分解机制的多目标进化算法(MOEA/D)[14]、基于参考点机制的非支配排序遗传算法(NSGAIII)[15]等。
鉴于以上背景,本研究围绕灌区梯级枢纽优化调度目标需求分析、模型构建及高效求解的关键科学问题,以茨淮新河插花枢纽、阚疃枢纽、上桥枢纽供水效益最优为目标,研究灌区中长期供水优化调度建模方法,采用多目标优化高效求解算法用于求解调度模型,基于优化调度方案集给出优选方案供调度决策者参考,同时与实际运行过程进行比较。本研究不仅可以丰富和完善灌区多目标调度建模理论与方法,且研究成果可直接应用于指导灌区调度方案的编制,具有一定的社会、经济和环境效益。
2 研究方法
2.1 茨淮新河概化模型
茨淮新河工程根据防洪、排涝、灌溉和航运等综合利用要求,自上游至下游依次兴建了茨河铺、插花、阚疃、上桥4座枢纽工程,其中茨河铺闸为颍河分洪闸,颍河水除在大水年份分洪进入茨淮新河外,一般年份不入茨淮新河。插花、阚疃、上桥为3座蓄水灌溉枢纽,灌区的灌溉水源主要来自上游颍河来水和插花、阚疃、上桥3座节制闸拦蓄当地径流,当灌溉水量不足时,依靠上桥一级抽水站和阚疃二级站从蚌埠闸上抽提淮河水源补给。灌区内水资源禀赋条件、水系分布、作物种植结构相对比较复杂,插花枢纽以上为小麦、玉米等旱作耕作区,插花枢纽至阚疃枢纽段为旱过渡发展区,阚疃枢纽至上桥枢纽段为稻茬麦耕作区,主要灌溉方式均由沿河和灌区内输水干渠两岸设多级面上站抽水进行灌溉。除农业灌溉需水外,茨淮新河灌区还存在城镇和工业用水需求。茨淮新河供需水概化如图1所示。
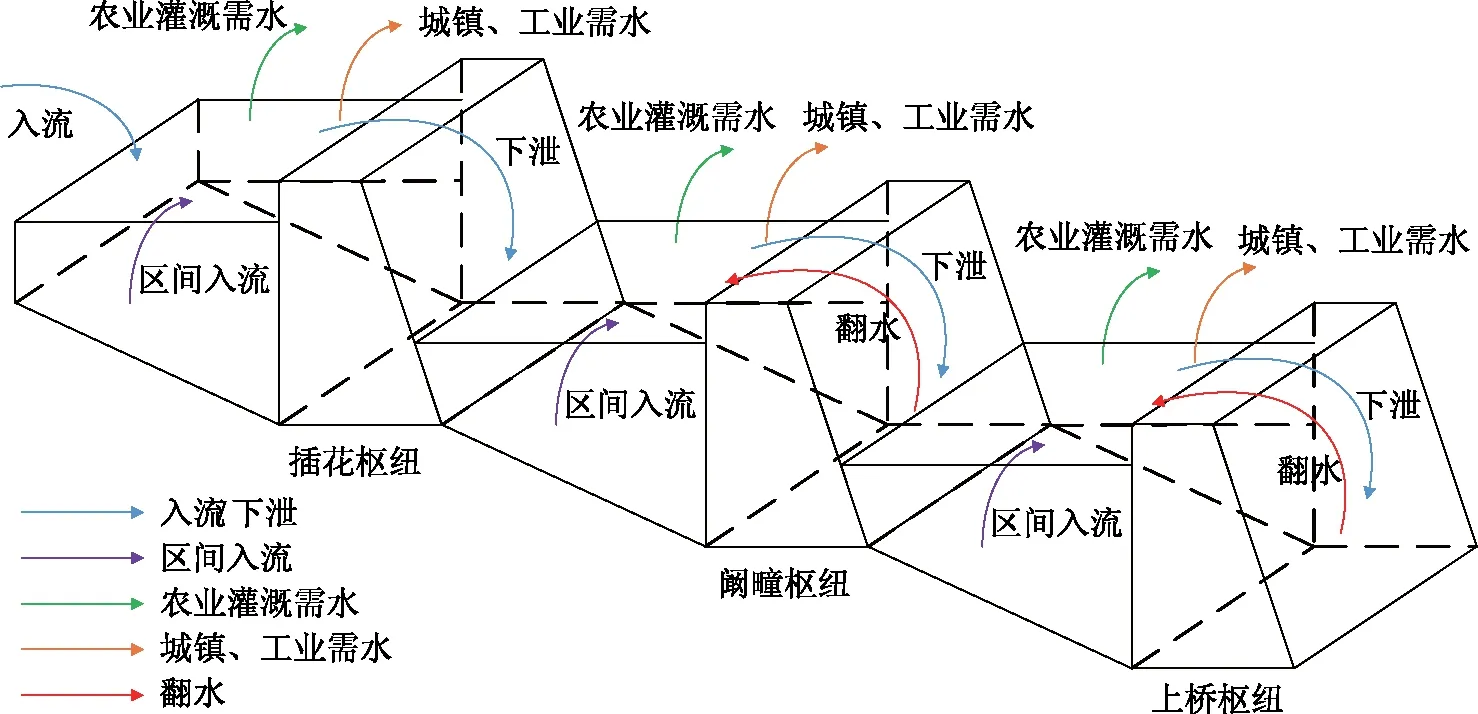
图1 茨淮新河供需水概化图
2.2 中长期供水优化调度模型
研究以茨淮新河各级枢纽为对象,针对各级枢纽开发利用过程中面临的供水需求问题,以供水保证率最高、上桥枢纽总抽提水量最小为供水效益调度目标,同时考虑防洪、通航、生态各时段约束条件,构建茨淮新河中长期多目标供水优化调度模型。
2.2.1调度目标
(1)供水保证率最高
(1)
(2)上桥枢纽总抽提水量最小
(2)
式中,n—枢纽总数;T—时段总数;Ri,t—第t个时段第i个枢纽段的下泄水量,万m3;Si,t—第t个时段第i个枢纽段从下游河段翻水至上游河段的水量,万m3。
2.2.2约束条件
(1)水量平衡约束
Ii,t+Pi,t+ΔVi,t-Wi,t-Ui,t=Ri,t-Si,t
(3)
ΔVi,t=Vi,t+1-Vi,t
(4)
(5)
Si,t=0 (Ri,t≥0)
(6)
式中,Ii,t—第t个时段第i个枢纽的入流水量,万m3;Pi,t—第t个时段第i个枢纽段的区间来水量,万m3;Vi,t—第t个时段第i个枢纽段的库容,万m3;Wi,t—第t个时段第i个枢纽段的农业灌溉需水量,万m3;Ui,t—第t个时段第i个枢纽段的城镇、工业需水量,万m3;ΔVi,t—第t个时段第i个枢纽段的库容变化值,万m3。
(2)水位约束
(7)
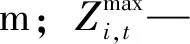
水位约束同时考虑防洪、通航、生态需水位要求。
(3)下泄流量约束
(8)
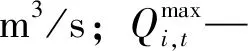
流量约束同时考虑防洪、通航、生态流量要求。
2.3 多目标优化算法
茨淮新河根据农业灌溉和城镇、工业用水2个不同供水效益目标,同时考虑防洪、航运、生态需求等边界条件,优化调度涉及多枢纽多时段等复杂决策过程,几乎不存在使各调度目标同时达到最优的单个调度方案。针对多目标优化调度模型求解,目前主要有2种方式:①通过权重法、约束法、隶属度函数法等将多目标优化问题转化为单目标问题进行逐步求解;②采用多目标优化算法进行求解,生成1组帕累托前沿非劣方案集。权重法、约束法、隶属度函数法等单次求解仅能得到1个调度方案结果,求解过程需要进行多次迭代才能得到1组方案集,计算效率相对低下。近年来,研究工作人员针对流域多目标优化调度问题展开研究,采用基于非支配排序遗传算法(NSGAII)建模求解,并取得了较为不错的效果,多目标进化算法领域仍然是目前研究发展的热点趋势之一,本文采用多目标优化算法进行建模和求解。
模型以茨淮新河插花、阚疃、上桥枢纽闸前水位为决策变量进行编码,以月为时间尺度,通过计算不同水位编码条件下供水调度目标值,进而得到供水效益最优的方案集,编码如下:
Xi,t={H1,1,H1,2,…,H1,T,H2,1,H2,2,
…,H2,T,H3,1,H3,2,…,H3,T}
(9)
式中,Xi—种群中每一个个体,对应一个优化调度方案;Xi,t—第i个水库第t个时段的坝前水位值,m;T—调度周期。
本文采用NSGAII算法进行调度模型求解,算法参数设置:种群规模为50,最大迭代次数为2000,其它参数与测试函数ZDT系列2目标测试实验相同。
(1)约束处理方式。若种群中存在个体违反约束条件,在算法的选择过程中进行处理,遵循下述原则:①若2个个体的解均未违反约束,按照目标函数值的非劣性确定二者之间的支配关系。②若其中2个个体的解违反约束,选取另1个不违反约束的个体。③若2个个体的解均违反约束,选取约束违背程度较小的个体。
(2)算法计算流程。①随机产生规模为N的初代种群,非支配排序后通过遗传算法的选择、交叉、变异3个基本操作得到第一代子代种群;②从第二代开始,将父代与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群;③通过遗传算法的基本操作产生新的子代种群,以此类推,直到满足程序结束的条件。算法流程如图2所示。
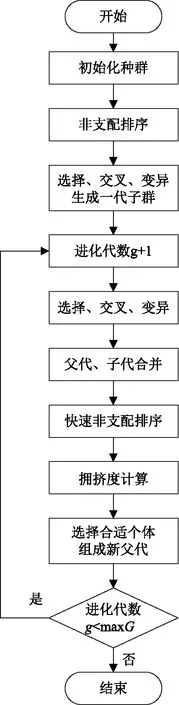
图2 算法流程图
3 模型求解与分析
本文选取茨淮新河灌区插花、阚疃、上桥枢纽1988年10月—2018年9月的基础数据资料,包含各级枢纽的来水、区间入流、农业灌溉需水、城镇和工业需水以及防洪、航运、生态水位约束条件等,基于非支配排序遗传算法(NSGAII)对中长期供水优化调度模型进行求解,根据模型求解结果,对比不同调度方案间的差别、优化调度与实际运行之间的差别,探究中长期供水优化调度目标效益、水位过程、抽水量过程之间的相互影响关系。
3.1 供水调度目标效益分析
算法迭代2000次计算得到的结果如图3所示。从帕累托前沿图可以看出供水保证率目标集中在0.955~0.966之间,总抽提水量在45.2亿~45.8亿m3之间,前沿呈现8个分布点,进一步对比调度目标可以看出,供水效益目标中目标①供水保证率最高与目标②上桥枢纽总抽提水量最小成反比关系,目标之前存在一定的制约性,进一步说明上桥枢纽抽水总量越多,泵站机组能耗越高,茨淮新河供水保证率越高。
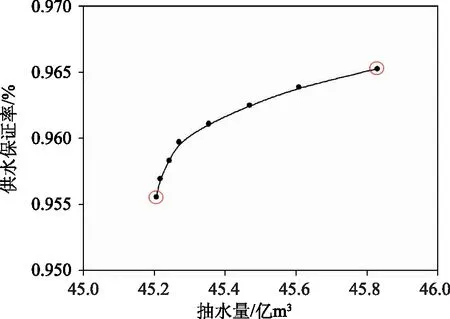
图3 NSGAII算法求解结果帕累托前沿图
3.2 调度方案对比分析
为了对比分析帕累托前沿图中2个供水目标效益之间的关系,本文选取帕累托前沿边缘2个相对极端方案(方案1供水保证率最高方案、方案8总抽提水量最小方案)进行对比分析,计算并绘制插花、阚疃、上桥水位抽水量过程图,如图4—8。通过1988年10月—2018年9月的插花闸前、阚疃闸前、上桥闸前水位以及上桥抽水量过程中可以看出,方案1和方案8在大部分月份水位、抽水量过程差别不大,但在来水偏枯、需水较大的月份(如1989年8—10月、1994年2—6月、1999年1—7月、2015年10月)存在一定的差异性。方案1和方案8在供水调度过程中,当来水充足时各个枢纽最大化抬高水位至最高限制水位,保证下一时段的供水的充足性;当来水较少时各个枢纽降低水位至最低限制水位,保证本时段的供水需求,若仍不能满足供水需求再采取翻水取水。但方案1在来水偏枯、需水较大的月份倾向于通过提高上桥抽水量来提高茨淮新河供水保证率,而方案8倾向于减少上桥抽水量,降低能耗。
为了进一步对比分析方案在不同水平年下的差异,通过水文频率排频计算选取25%频率丰水年(2007年)、50%频率平水年(2013年)、75%频率枯水年(1999年),计算并绘制插花、阚疃、上桥水位抽水量过程图,如图9—12。在丰水年、平水年中,方案1和方案8水位和抽水量过程没有差别,丰水年通过优化调度方案实施无需进行上桥抽提水基本可以满足供水需求,插花、阚疃、上桥水位基本维持在各个时段的最高限制水位。平水年通过调节各个枢纽的闸前水位,在一定程度上减少上桥抽提水量达到满足各个时段的供水需求。在枯水年,方案1和方案8存在一定的差异,方案1上桥总抽提水量更大,供水保证率更高,水位变化相对较为平缓,方案8上桥总抽提水量更小,供水保证率相对较低,但水位波动更大。
本文收集了2002—2017年间上桥实际抽水量数据,通过方案1、方案8和实际抽水量对比,如图13所示。可以看出,除2004年外,其他年份优化调度计算得到的抽水总量小于实际抽水总量。在2002—2017年总抽水量计算上,方案1和方案8相比于实际抽水量分别减少了38%、37%,进一步说明了供水优化调度方案具备一定的优越性。
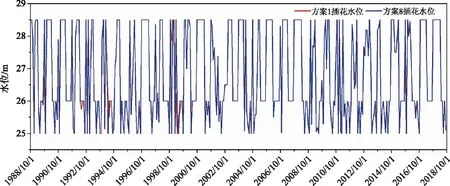
图4 方案1、方案8插花枢纽水位对比图
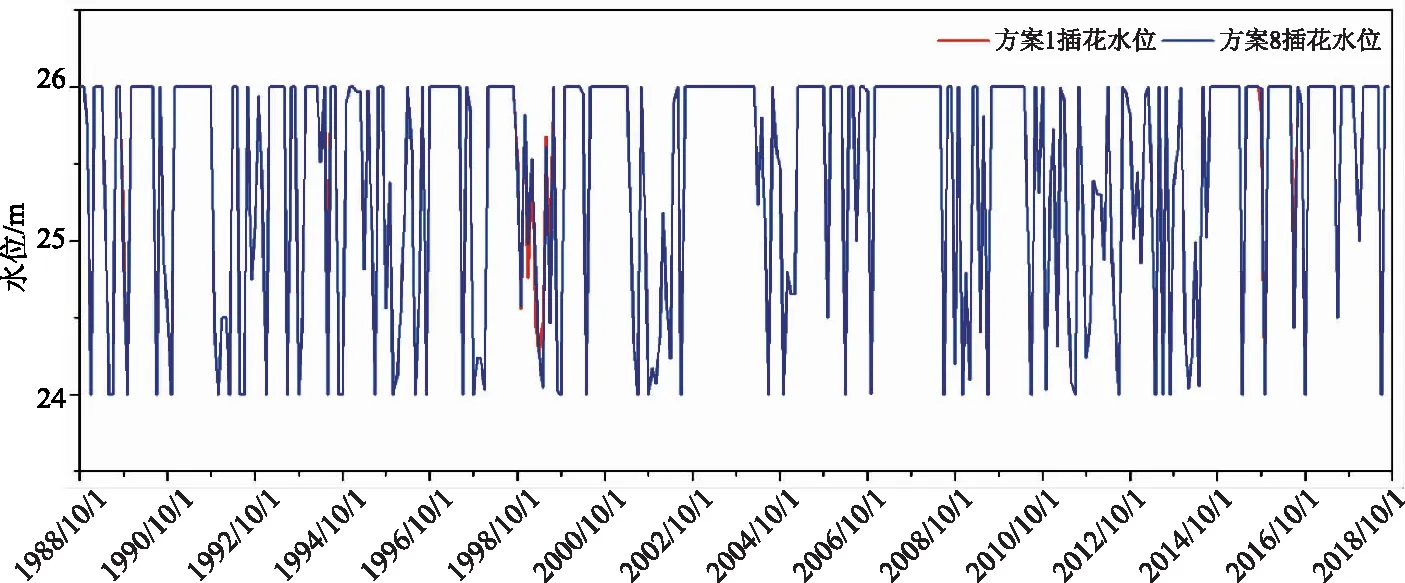
图5 方案1、方案8阚疃枢纽水位对比图
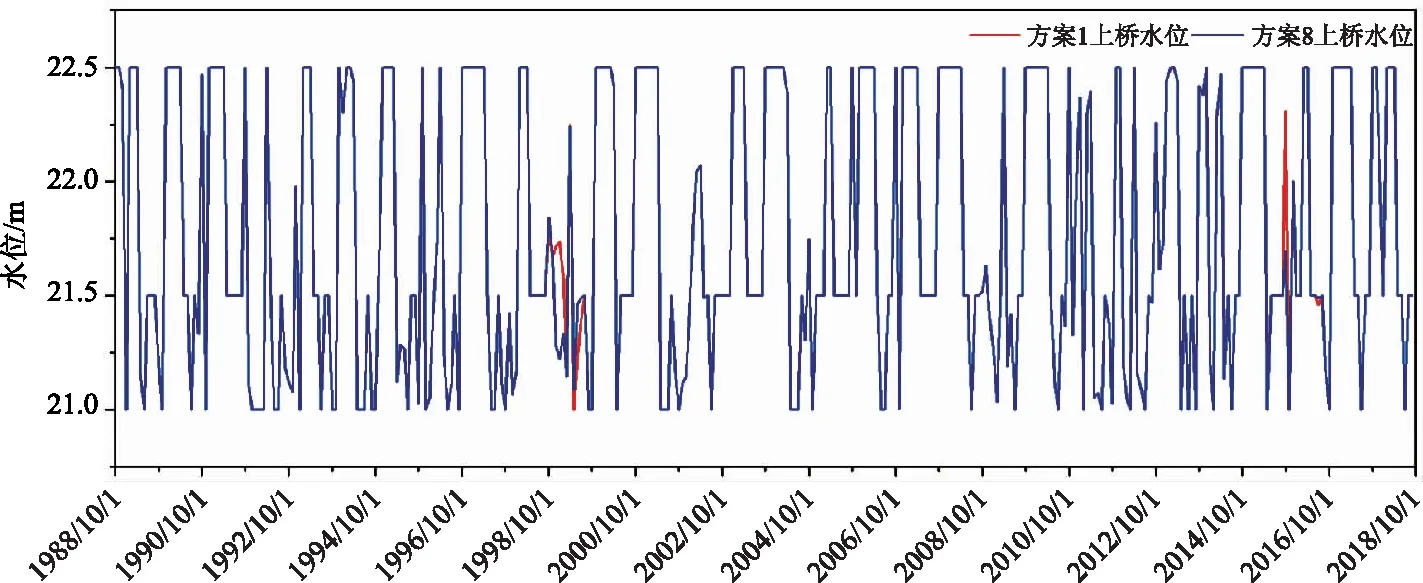
图6 方案1、方案8上桥枢纽水位对比图
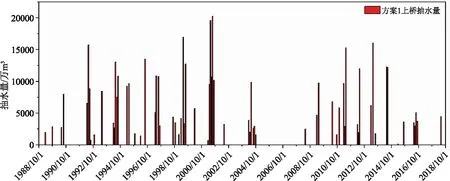
图7 方案1上桥枢纽抽水量过程图
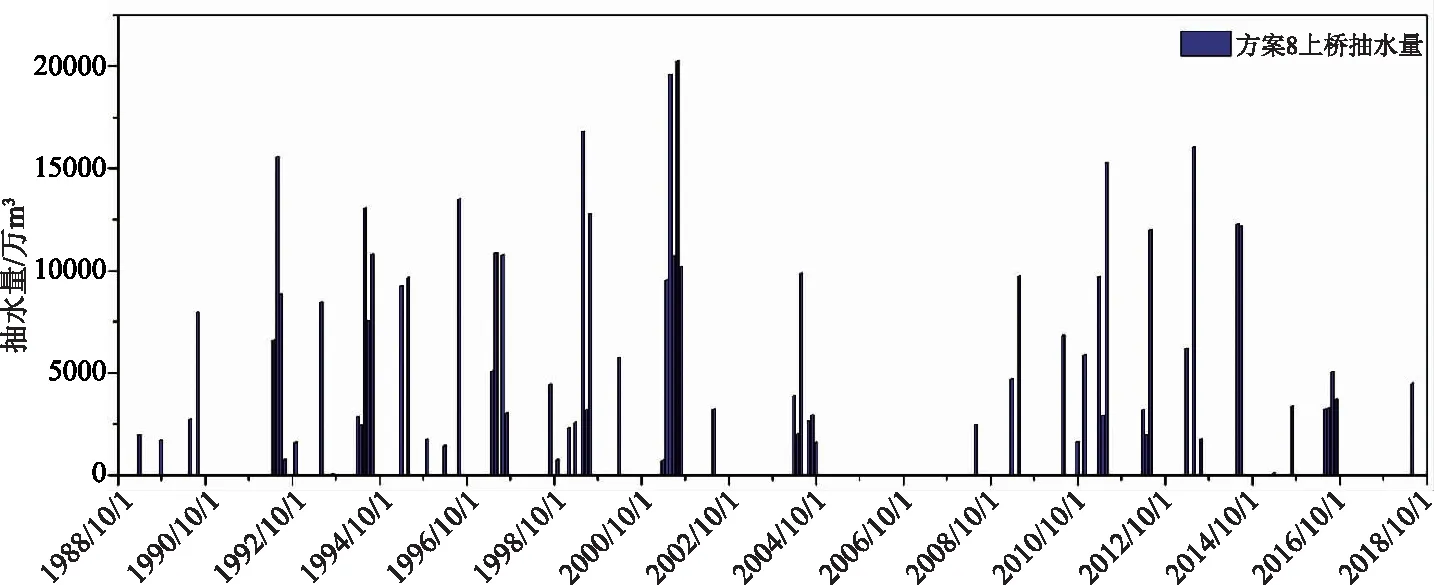
图8 方案8上桥枢纽抽水量过程图
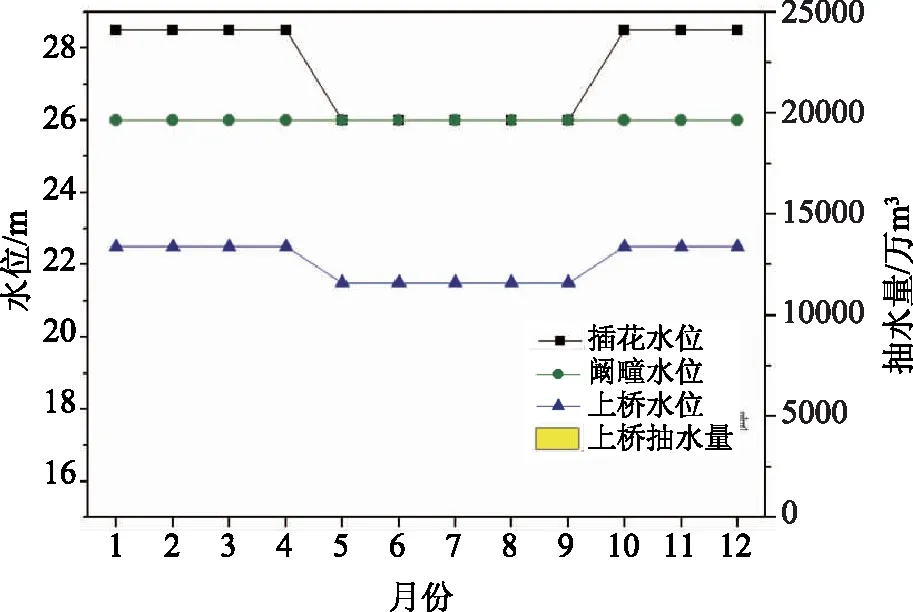
图9 丰水年插花、阚疃、上桥水位抽水量过程图
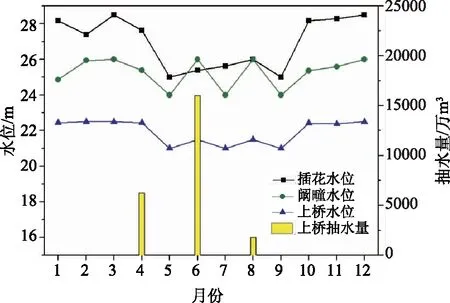
图10 平水年插花、阚疃、上桥水位抽水量过程图
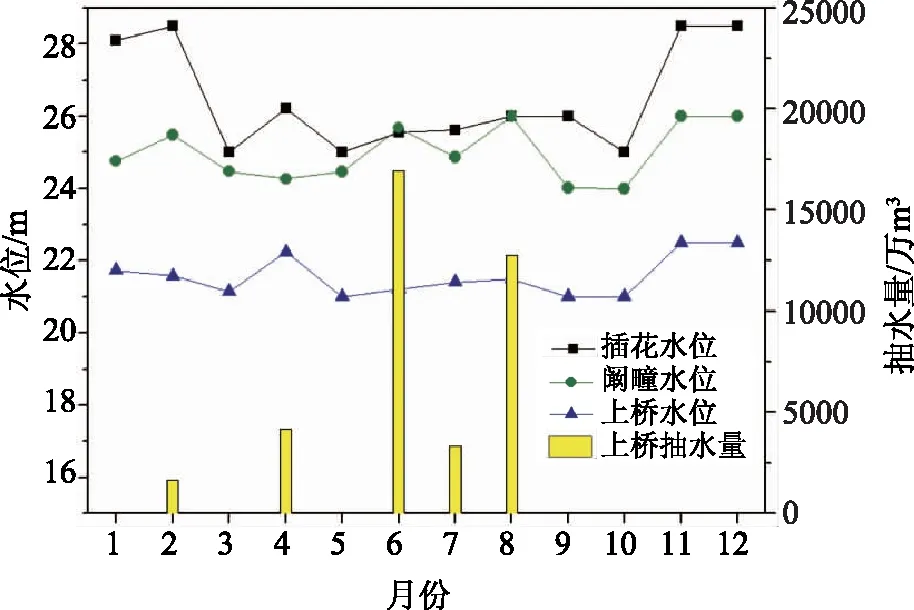
图11 枯水年方案1插花、阚疃、上桥水位抽水量过程图
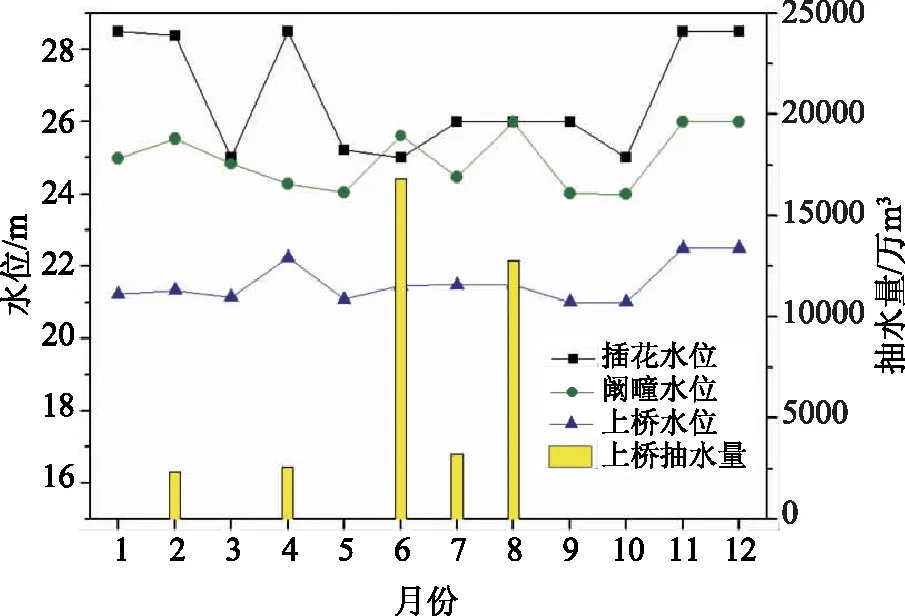
图12 枯水年方案8插花、阚疃、上桥水位抽水量过程图
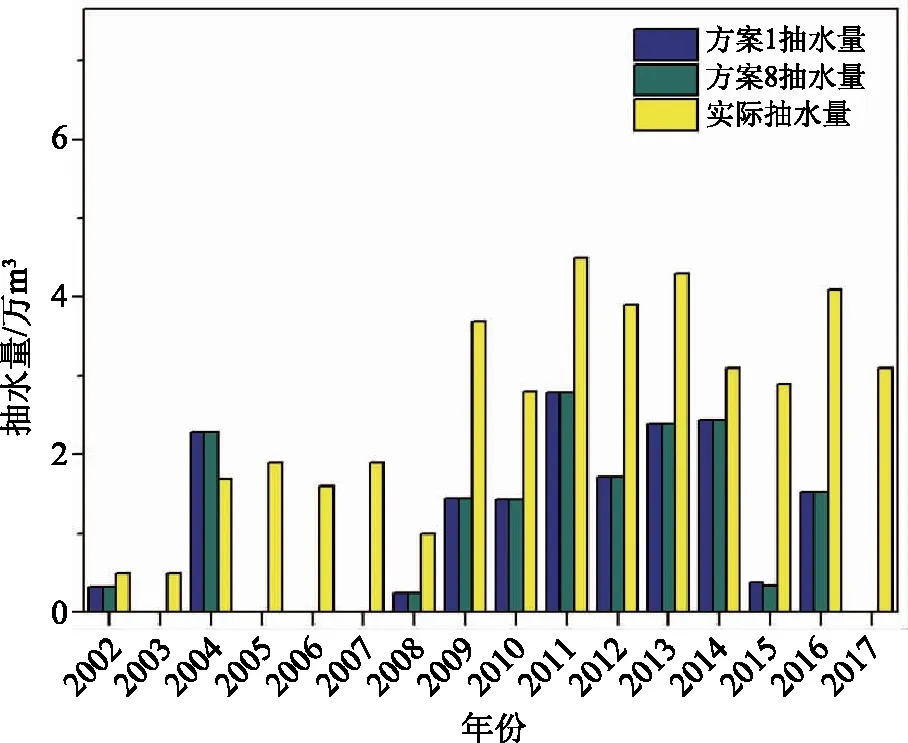
图13 方案1、方案8、上桥实际抽水量对比结果图
4 结论
(1)研究综合分析了影响茨淮新河灌区供水效益的供水保证率、总供水能耗2个目标以及防洪、生态、航运等约束条件,建立了梯级枢纽多周期多目标优化调度模型,同时采用先进的多目标算法进行求解,并给出优化调度方案集,提供了一种全面综合分析建模的求解思路。
(2)研究对比了丰、平、枯水年优化调度方案,发现水位偏枯的年份,不同的优化调度方案差距较大。今后研究中,可结合不确定性来水条件做进一步分析。
(3)研究对比了优化调度方案与实际运行方案,在保证在满足供水保证的条件下,优化调度方案最高可减少37%总抽水能耗,优化调度方案的结果可供调度决策者参考,给予实际指导意义。
