“光的折射、全反射”试题类型及其解答方法分析
2022-08-29安徽张玉龙
安徽 张玉龙
光的折射、全反射知识是历年高考及各地区模拟考的热点内容,涉及的题目以计算题为主,要求学生能够理解相关物理概念,能正确地画出光路图,还要求学生具有一定解决物理问题的计算能力,具备较高的物理学科核心素养。纵观历年光学试题,显然每年试题设置的物理情境均有所变化,但各种类型试题的解答方法仍有规律可循,下面是笔者对本考点试题类型的概括及解题思路的总结,希望对教师和学生有所帮助和启发。
一、光在棱柱中传播
光与棱柱相结合是光学试题的基本模型,通常以棱镜柱为载体巧设物理情境,主要考查学生对光的反射定律、折射定律、全反射现象的理解与应用,学生需要先理解题目的考查意图并正确地画出光路图,然后借助数学知识处理相关问题。

图1
【解析】光路图如图2所示。

图2
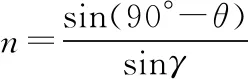
解得γ=30°
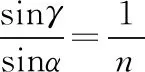
解得α=60°
故MB∥NA,则MN=AB
h=lOM·cotα=2dtanγ·cotα
解得d=6 cm,所以玻璃砖厚度为6 cm。
【点评】本题意在考查光在平行玻璃砖中的传播特点,题中把折射率n作为已知量,对平行玻璃砖,学生做出光路图后就能迅速判断出ON与MB光线是平行的,再以折射率n为连接点即可求解相关问题。
【例2】(2018·全国卷Ⅱ·34)如图3,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
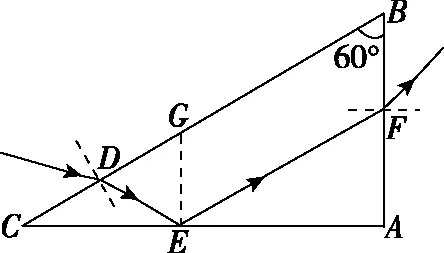
图3
(ⅰ)求出射光相对于D点的入射光的偏角;
(ⅱ)为实现上述光路,棱镜折射率的取值应在什么范围?
【解析】(ⅰ)根据题意可以做出光路图如图4所示,n为棱镜的折射率,i1和r1分别是该光线在BC面上的入射角和折射角,i2和r2分别是该光线在AC面上的入射角和反射角,i3和r3分别是该光线在AB面上的入射角和折射角。

图4
当光从BC面上折射进入棱镜中,由折射定律得

光线在AC面上发生全反射时,由反射定律得
i2=r2②
光线在AB面上发生折射,由折射定律有
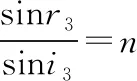
根据光路图,由几何关系得
i2=r2=60°,r1=i3=30° ④
则F点的出射光相对于D点的入射光的偏角为
δ=(r1-i1)+(180°-i2-r2)+(r3-i3) ⑤
由①②③④⑤式得δ=60°
(ⅱ)根据全反射的知识,光线在AC面上发生全反射,在AB面上不发生全反射,有
nsini2≥nsinC>nsini3⑥
式中C是全反射临界角,满足
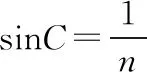
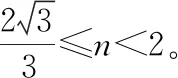
【点评】本题考查光在三棱镜中的传播特点,难点在于寻找不同夹角之间等量关系,能否准确的画出光路图是解答本题的关键,且光路图画的越准确越有助于解题(有时根据图像就可以估测出特殊角的大小)。
二、光在球形(半球形)或圆形(弧形)介质中传播
球形(半球形)或圆形(弧形)具有对称性,可以灵活地设计光路和设置问题。解答这类题型需要一定的技巧,学生先要对物理概念有较深的理解,进而画出临界光路图,必要时还要使用对称性或代入法对其进行反向论证,因为试题中的角度往往是常见的特殊角,所以学生还需要熟悉三角函数知识。
【例3】如图5,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直)。已知玻璃的折射率为1.5。现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线)。求:
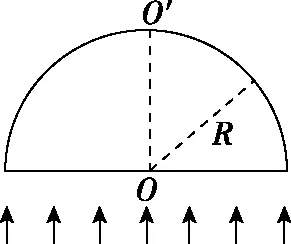
图5
(ⅰ)从球面射出的光线对应的入射光线到光轴距离的最大值;
【解析】(ⅰ)如图6所示,从球面射出的光线对应的入射光线到光轴距离有最大值时,这个入射光刚好发生全反射,临界角为C

图6

入射光的光线到光轴的最大值为
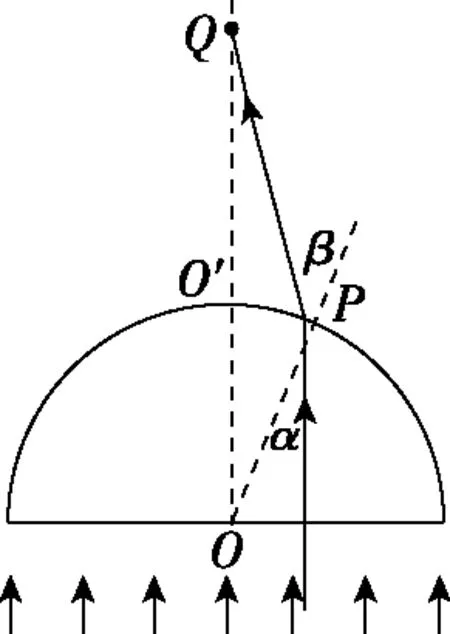
图7
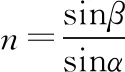
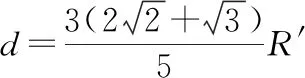
【点评】解答此类题型的关键是找出临界光线,过圆心做出临界光线在不同介质分界面上的法线,光路图应尽量与实际相符,从而找到物理量间的关系,最后使用正弦定理得出答案。
三、光在光纤介质中传播
光纤是光的全反射的一个重要应用,光在光纤中传播的过程中不仅涉及光的折射定律,还涉及光的全反射现象。这类试题往往模型固定、题型单调,学生只要对其熟悉便能轻松解题。
【例4】图8为一光导纤维(可简化为一长玻璃丝)的示意图,玻璃丝长为L,折射率为n,AB代表端面。已知光在真空中的传播速度为c。
(ⅰ)为使光线能从玻璃丝的AB端面传播到另一端面,求光线在端面AB上的入射角应满足的条件;
(ⅱ)求光线从玻璃丝的AB端面传播到另一端面所需的最长时间。
【解析】(ⅰ)设光线在端面AB上C点的入射角为i,折射角为r,由折射定律有
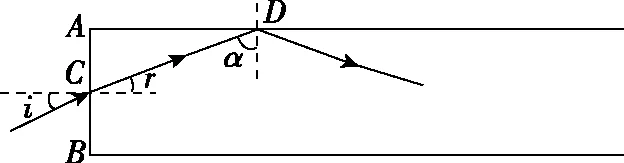
图9
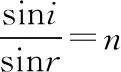
设θ是光线在玻璃丝内发生全反射时的临界角,则
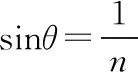
设光线射向玻璃丝内壁D点的入射角为α,为了使该光线可在光导纤维中传播,
应有α≥θ③
由几何关系得α+r=90° ④
光速在玻璃丝轴线方向的分量为vz=vsinα⑦
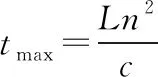
【点评】光从光纤的端口折射进入时,若使光在光纤中传播发生全反射,需要光从端口入射时的入射角越小越好,且当光在光纤中恰好发生全反射时对应的传播路程最大。
四、光与运动相结合
当光源移动时,光线在分界面的出射点也会发生位置变化,此类试题往往在不同方向上存在着定量的运动关系,学生需在读懂题目的前提下建立不同运动方向的内在等量关系,最终结合光学知识突破相关问题。
【例5】如图10所示,一足够大的水池内盛有某种透明液体,在水池的底部中央放一点光源S,当光源S以速度v1匀速上升的同时,发现在液体表面形成亮斑的半径以速度v2匀速减小,且v1=v2,求:
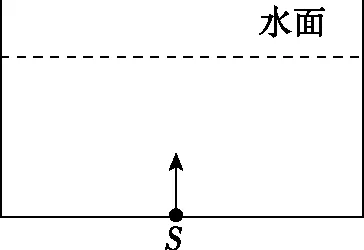
图10
(ⅰ)液体的折射率;
(ⅱ)若其中一条光线从池底以30°的入射角入射到液体与空气的界面上,则它的反射光线与折射光线的夹角为多少。
【解析】(ⅰ)当光源向上移动时,光路图如图11所示,C为全反射的临界角,亮斑在t时间内移动的距离为ΔR,光源在t时间内上升的距离为ΔH

图11
则由几何关系可得
ΔR=v2·t
ΔH=v1·t
(ⅱ)如图12所示,i=30°
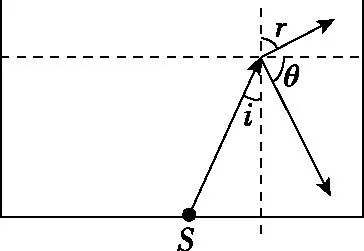
图12
θ=180°-r-i=105°
【点评】这类题型比较新颖,物理量间等量关系隐含较深,学生很难直接通过一条光线找到等量关系,则需要做出几条完整的传播光线,分别在不同方向上列出对应的位移、速度公式,最后再通过光学知识寻找几何关系。
五、光与能量相结合
当光从光密介质射入光疏介质时,在没有发生全反射之前,反射光的强度会随着入射角的增大而增大,当发生全反射时光强达到最大。
【例6】为了研究某种透明新材料的光学性质,将其压制成半圆柱形,如图13所示。一束激光由真空沿半圆柱体的径向与其底面过O的法线成θ角射入。CD为光学传感器,用以探测光的强度。从AB面反射回来的光强随角变化的情况如图14所示。现在将这种新材料制成的一根光导纤维束弯成半圆形,如图15所示,暴露于空气中(假设空气中的折射率与真空相同),设半圆形外半径为R,光导纤维束的半径为r。求:
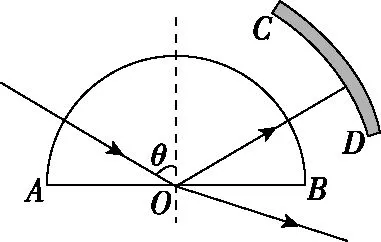
图13
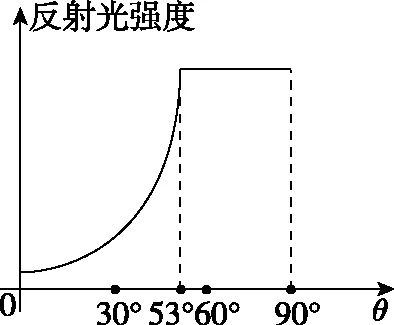
图14
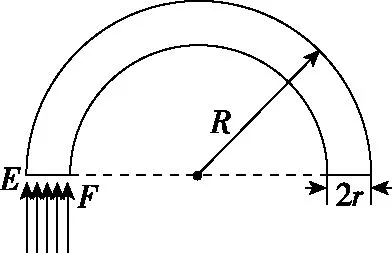
图15
(ⅰ)这种新材料的折射率;
(ⅱ)用同种激光垂直于光导纤维的端面EF射入,若该束激光不从光导纤维的侧面外泄,则弯成的半圆形的半径R与光导纤维半径r应满足的关系。
【解析】(ⅰ)在折射过程中未发生全反射时,反射光线的强度随着入射角的增大而增大,当刚好达到临界角时,反射光强度达到最大且此后不再变化,由图14可知
全反射临界角C=53°
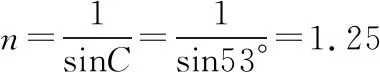
(ⅱ)当入射光线越接近E点时,则光在光纤中的入射角越大,就越容易发生全反射,因此激光不从光导纤维束侧面外泄的临界条件是入射光在光导计准侧面发生全反射,临界光路图如图16所示
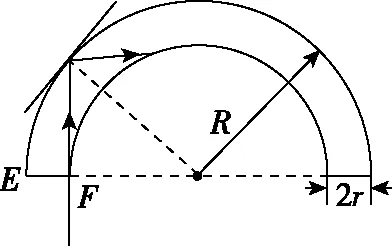
图16
解得R=10r,因此只要R≥10r,该束激光就不会从光导纤维的侧面外泄。
【点评】这类试题从能量方面对光的全反射进行考查,考查的知识点比较细致,学生需要应用折射率、临界条件等知识列式求解。
六、光路与色散相结合
该类题型主要以选择题为主,考查学生对光的本质属性及折射率的理解,学生只要熟记常见的可见光(红橙黄绿蓝靛紫)的频率大小关系,就可以快速解答。
【例7】如图17,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线。则________。
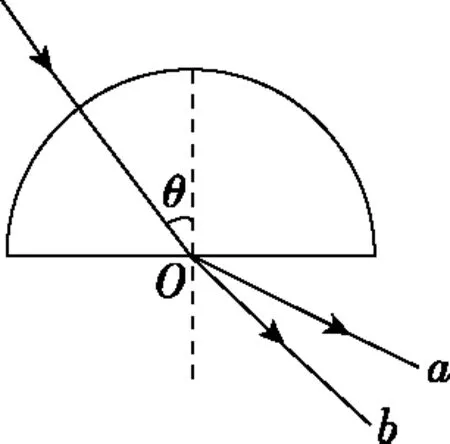
图17
A.在玻璃中,a光的传播速度小于b光的传播速度
B.在真空中,a光的波长小于b光的波长
C.玻璃对a光的折射率小于对b光的折射率
D.若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失
E.分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距
【解析】由图17可知,玻璃砖对a光的折射率大于对b光的折射率,故C错误;在玻璃中,a光的传播速度小于b光的传播速度,故A正确;a光的频率大于b光的频率,在真空中,a光的波长小于b光的波长,故B正确;因a光的折射率大,所以当θ角逐渐变大时,折射光线a首先消失,故D正确;a光的波长小于b光的波长,分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距小于b光的干涉条纹间距,故E错误,因此正确选项为ABD。
【点评】这类题目的考点并不难,学生可以通过动手做实验加强对色散现象的记忆及光干涉条件的掌握。
七、总结
光的折射、全反射知识是高中物理光学考试的重点内容,教师在指导复习的过程中,要善于引导学生对试题类型进行归纳,让学生熟悉各种类型下光学题目的特征及解题方法;同时,学生也要有针对性地进行适当练习,提升数学计算能力。
