两个异种点电荷电场中零势能面的探讨
——以一道高考模拟题为例
2022-08-29广东邹范勇
广东 邹范勇
《普通高中物理课程标准(2017年版2020年修订)》中物理教学的基本理念旨在培养适应学生终身发展和社会发展需要的核心素养,尤其强调推理论证、质疑创新与合作交流等必备品格和关键能力。在高三复习备考中,笔者从一道高考模拟题出发,通过质疑、论证和探索,对题设条件的自洽性进行了讨论和证明,并对题设问题进行拓展,一方面可以锻炼学生的科学思维,提升解决问题的能力;另一方面,可以使学生举一反三,提高备考复习效率。
1.原题
(2021·贵州省新高考联盟复习考·2)在水平直线上的A、B两点分别固定有不等量点电荷,其中A处为正电荷,B处电荷电性未知,O1为A、B连线中点。由绝缘材料制成的光滑圆轨道的圆心O2在AB连线上A点左侧,其轨道平面与AB在同一水平面内,如图1所示。在轨道上穿一带正电的小球并置于轨道上的某一点P,给小球一沿轨道切线方向的初速度,小球恰好能沿轨道做匀速圆周运动,小球可视为质点,下列说法正确的是

图1
( )
A.B处点电荷带负电,其电荷量小于A处电荷电荷量
B.小球沿轨道运动过程中,小球的电势能不变
C.小球沿轨道运动过程中,小球受到的电场力大小不变
D.小球沿轨道运动过程中,轨道对小球的弹力大小不变
2.解析
由于小球做匀速圆周运动,动能不变,根据能量守恒定律,小球在圆轨道上运动时的电势能也不变,则圆轨道一定处在电场的一个等势面上,所以B选项正确。
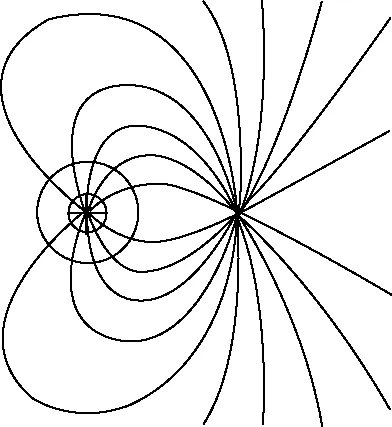
图2 不等量异种点电荷的电场线
由于电场强度的叠加,轨道上各处的场强大小不都相等,故小球受到的电场力大小会发生变化,故C选项错误。
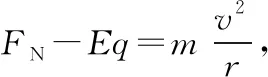
【答案】B
3.质疑
题设中的关键条件是小球能做匀速圆周运动,已知条件是否自洽呢?或者说,异种电荷是否真的存在一个球形的等势面呢?如果存在,球心的位置在何处?结合题设条件,能否确定出B处小球的电荷量大小与A处小球的关系呢?
4.论证
以A为坐标原点,A、B连线为x轴,在水平面内建立xAy坐标系。设A处点电荷的电荷量为q1,B处点电荷的电荷量为q2,A、B距离为l,则A、B点的坐标分别为(0,0)、(l,0)。在电势为φ的等势面上,设任意一点P的坐标为(x,y),其满足如下方程(为便于讨论,设静电力常量为1)。
①
5.探索
应用Geogebra软件,可以方便地探索两个点电荷的等势面的分布情况。在Geogebra中建立滑动条q1、q2、φ,在命令栏中输入“q_1/(x2+y2)^0.5+q_2/[(x-l)2+y2]^0.5=φ”,打开“开启跟踪”选项,移动滑动条改变参数q1、q2、φ的值,得到如下等势面的分布图。
如图3,4所示,同种点电荷的等势面随电势升高连续变化,逐渐分化为两个电势相等且分别围绕两个点电荷的等势面;而后随电势升高,等势面越发趋近以点电荷为球心的球面,但由于另一个点电荷的存在而不会完全变成球形。

图3 等量同种点电荷
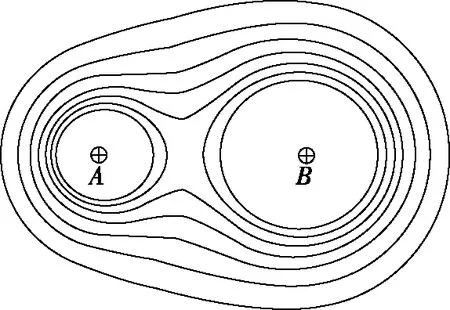
图4 不等量同种点电荷
如图5,6所示,异种点电荷的等势面,当电势为负值时,是围绕q2的曲面,当电势为正值时,是围绕q1的曲面。但当电势为零时,等势面会发生突变,等量异种点电荷的零势能面会突变为平面,不等量异种点电荷的零势能面会突变为球面。
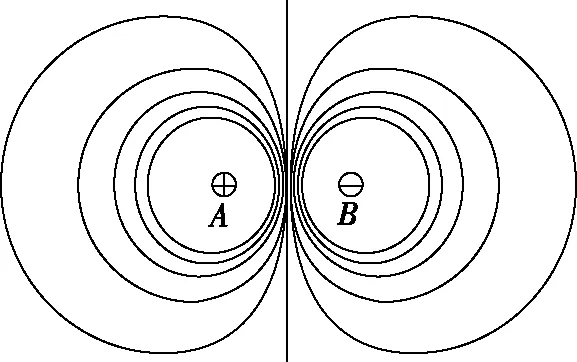
图5 等量异种点电荷

图6 不等量异种点电荷
6.证明
不等量异种点电荷形成的电场中,必存在球形的零势能面。
(1)代数证明
令q1=q,q2=-kq,则电势φ=0时,方程①变为
②

k≠1时,化简方程②得
③
(2)几何证明
k=1时,方程②代表到点A和点B距离相等的点的集合,即两点连线的中垂面。
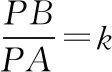

图7
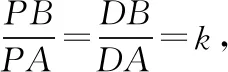
不等量异种点电荷电场中的球形等势面,其球心位置O和球面半径R完全由两个点电荷的电荷量比值k和相对距离l决定,此模型在高考模拟题、自主招生试题和竞赛题中时有出现,下面结合两个例题进行拓展。
7.拓展


图8
( )
A.q2恰好位于圆轨道的圆心处
B.q2带正电,电荷量为2q
C.小球在B点受到的电场力最大
D.小球的电势能保持不变

【答案】BD
【点评】本题很好的考查了两个不等量异种点电荷电场的基本特点以及零势能面的半径与两点电荷距离的关系,以小球在电场中做匀速圆周运动为突破口,可判断小球的运动轨迹必与异种点电荷电场中的零势能面重合。
【例2】(原创)如图9所示,两个点电荷q1=+q、q2=-2q固定在绝缘光滑水平面上。质量为m、电荷量为-q的带电小球在水平面内沿着半径为R的光滑绝缘圆轨道内侧做完整的匀速圆周运动,已知圆轨道圆心O在两点电荷的连线上,静电力常量为k,求:

图9
(1)小球的速度至少为多少;

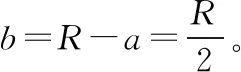
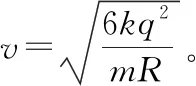

解得Q=q,所以需要在圆心O放置负电荷,其电荷量至少为q。
【点评】本题第(1)问结合质点在轨道内部做完整圆周运动的条件,考查了不等量异种点电荷零势能面的基本特征;第(2)问中,利用在零势能面的球心处放置点电荷只改变电势高低,不改变等势面形状的特点,进一步加深了对不等量异种点电荷电场中球形等势面的理解。
8.结论

