波形腹板阻尼器人字形支撑框架的抗侧性能研究

2022-08-29王威徐善文罗麒锐孙壮壮王冰洁刘磊

中南大学学报（自然科学版） 2022年7期

王威，徐善文，罗麒锐，孙壮壮，王冰洁，刘磊

(西安建筑科技大学土木工程学院，陕西西安，710055)

在建筑结构抗震领域，纯钢框架结构在地震荷载作用下往往侧移较大，难以保证结构的安全。因此，基于抗震的考虑，可以在纯钢框架的基础上设置支撑结构，形成钢框架支撑结构体系。在地震荷载的作用下，支撑结构作为抗震的第1道防线，钢框架结构作为抗震的第2道防线，能够有效保证结构的安全。

现有的支撑结构主要分为偏心支撑[1-3]与中心支撑结构[4-7]，偏心支撑结构在其与主梁的连接处设置了消能梁段，消能梁段本身通过屈服进行耗能。学者们针对不同的支撑形式进行了大量研究。支撑结构按形状一般可分为Y 形[8]、K 形[9]和人字形支撑[10]等。在钢框架结构中设置不同的支撑体系，可以有效提高钢框架结构的抗侧刚度和承载性能。传统的偏心支撑结构对于框架柱和支撑的承载力要求较高，可使地震荷载作用下的消能梁段在达到极限承载力之前不屈服；另一方面，消能梁段在地震荷载作用下发生剪切变形，支撑框架结构的主梁容易被破坏，其更换及修复较为繁琐。为克服以上不足，人们在钢框架结构的偏心支撑上设置消能阻尼器，利用金属阻尼器的弹塑性变形消耗地震能量。在地震作用下，将结构的塑性变形及损伤破坏集中于阻尼器上，阻尼器相当于结构的“保险丝”，可保护整体结构的安全。

然而，现有的阻尼器往往构造较复杂，制作成本较高，对工作环境要求高。例如黏滞阻尼器[11-12]对密闭性有一定的要求；电磁阻尼器[13-14]虽然有着可靠性高、系统使用寿命长等优点，但其造价较高，难以在普通建筑中广泛应用。为此，本文作者首先设计一种波形腹板阻尼器，其形式构造简单，造价较低。其次，通过试验研究波形腹板阻尼器的滞回性能，并在偏心人字形支撑框架结构中布置阻尼器，以增加框架结构的附加阻尼，减小地震作用对框架结构的影响。最后，借助于ABAQUS 有限元软件，分析波形腹板阻尼器人字形支撑框架结构的抗侧性能。

1 阻尼器的设计及试验

1.1 阻尼器的设计

本文分别设计横向波形腹板阻尼器(CSPD-H)与竖向波形腹板阻尼器(CSPD-V)这2 个阻尼器，阻尼器的腹板及翼缘板采用由平钢板弯折成的波形板，波形腹板采用正对称的形式布置。阻尼器的各个部件均采用Q235 普通钢材，翼缘板、腹板分别与上下端板焊接。为保证波形腹板拥有充足的变形空间，在翼缘板与腹板之间预留出10 mm的空隙。波形板的厚度均设置为6 mm，上下端板厚度设置为16 mm；波形腹板的高度及宽度均为264.8 mm，波形板的弯折角度为45°。阻尼器的具体构造如图1所示。

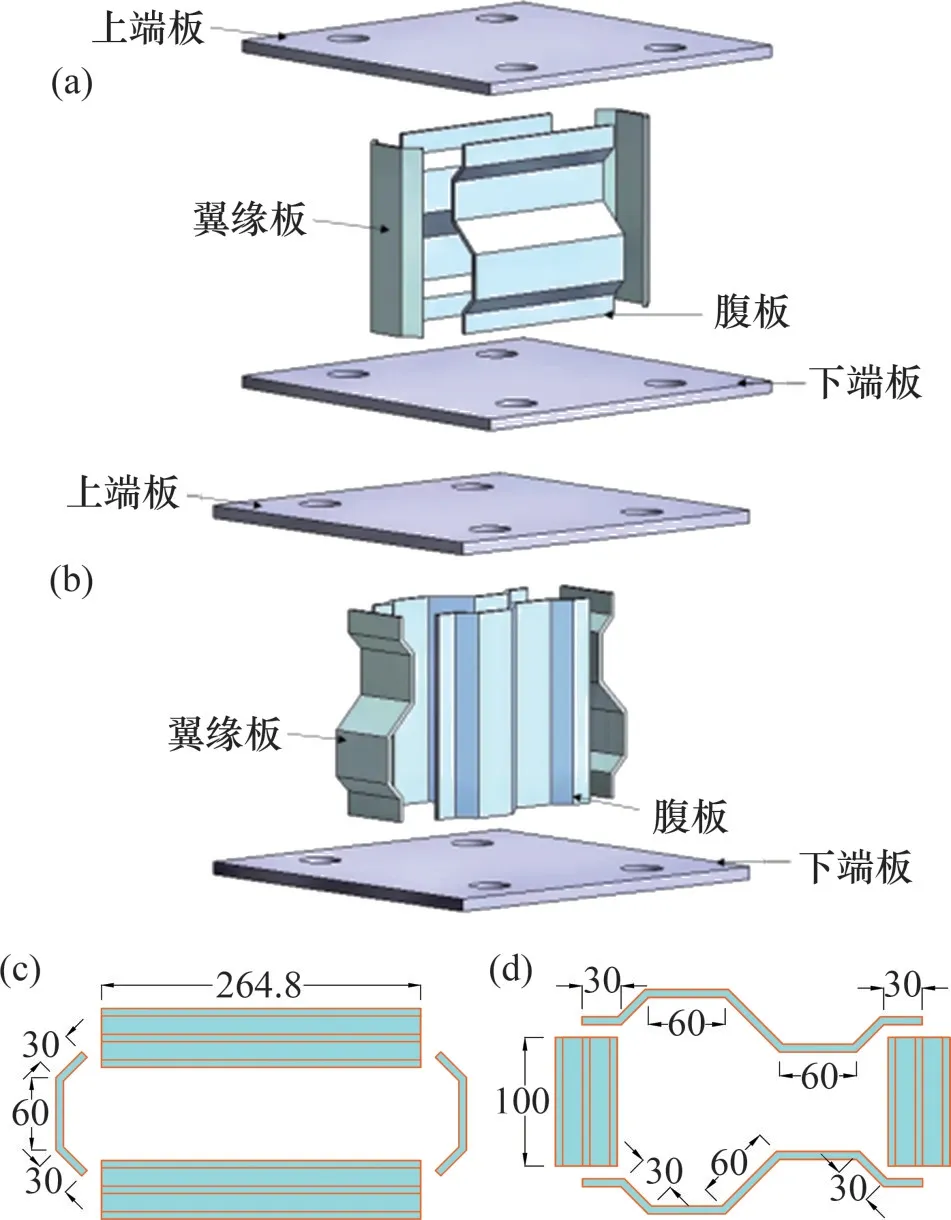
图1 阻尼器的构造Fig.1 Construction of damper

1.2 试验

在西安建筑科技大学结构与抗震实验室进行拟静力试验，由MTS 电液伺服试验机施加循环往复荷载，研究波形腹板阻尼器的滞回性能。根据JGJ/T 101—2015“建筑抗震试验规程”[15]中的要求，采用荷载-位移双控制法，阻尼器试件屈服前采用力控制，试件屈服后改用位移控制，每级位移加载3 次，试验加载制度如图2 所示。图2 中，Py为初始荷载，Py,n为第n级荷载；Δy为初始位移，Δy,n为第n级位移。按照GB/T 2975—1998“钢及钢产品力学性能试验取样位置及试样制备”[16]的要求，从阻尼器母材中切取3个标准拉伸试件进行材性试验，测得的数据取平均值，得到钢材的力学参数。本次试验的基本流程如图3所示。

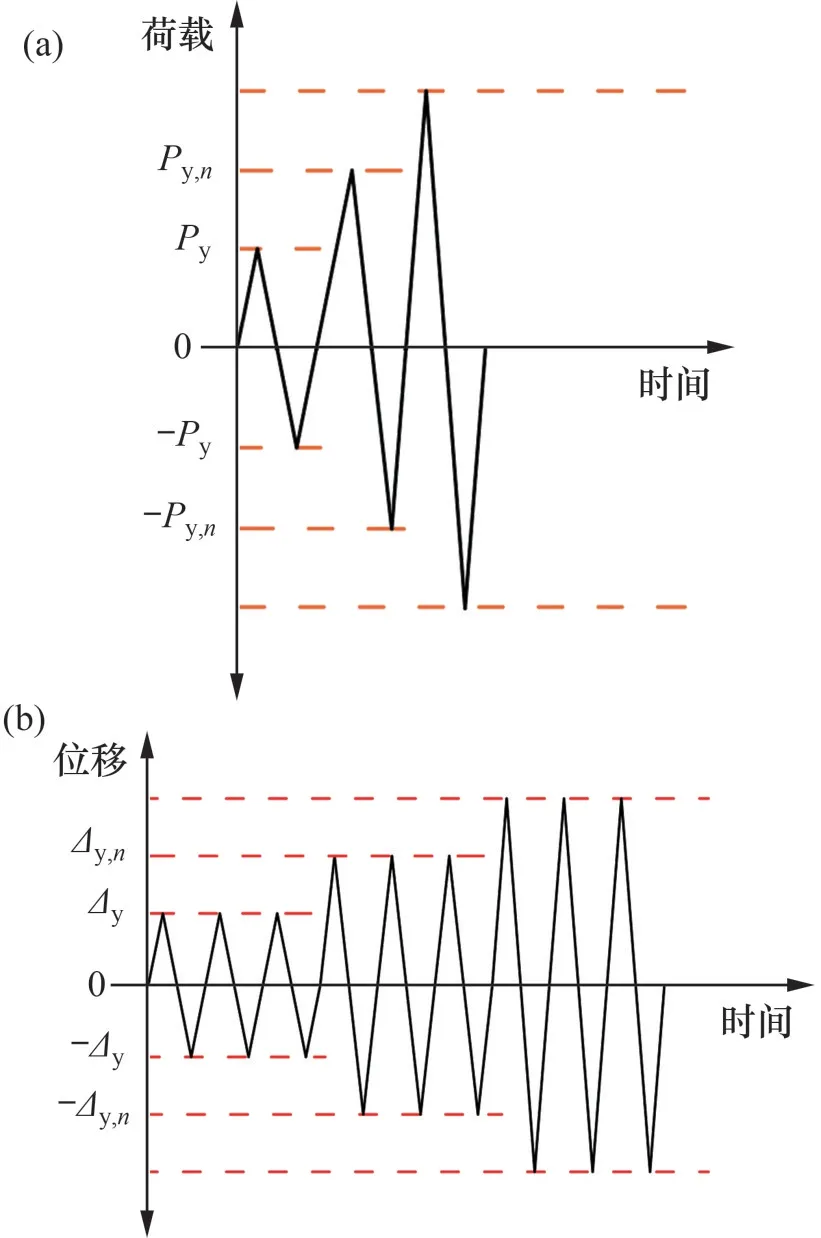
图2 试验加载制度Fig.2 Test loading system

图3 试验流程Fig.3 Test flow

1.3 试验结果及有限元验证

1.3.1 试验结果

试件的滞回曲线与骨架曲线如图4所示，其中Δ为阻尼器水平方向加载位移，P为阻尼器水平方向荷载。由图4(a)可见：试件CSPD-H 与CSPD-V的滞回性能良好，滞回曲线相对饱满。在水平荷载作用下，2 个阻尼器试件均经历了弹性、弹塑性、塑性及破坏阶段。在弹性阶段，阻尼器的变形较小，耗能较少；进入屈服阶段以后，阻尼器的波形腹板产生较大屈曲变形，阻尼器的耗能增加；翼缘板可对阻尼器提供一定的侧向约束，防止阻尼器发生面外倾斜。由图4(b)可见：试件CSPD-H 的峰值承载力约为117 kN，试件CSPD-V的峰值承载力约为211 kN。试件CSPD-V的承载力明显高于试件CSPD-H的承载力，这是因为波形腹板的布置形式对阻尼器的力学性能有较大影响。对于竖向波形腹板阻尼器(CSPD-V)，由于腹板波形边与上下端板焊接面积大，抗侧刚度大，因而其承载力较高；而横向波形腹板阻尼器(CSPD-H)只有腹板的平直边与上下端板焊接，焊接面积小，因而其承载力较低。

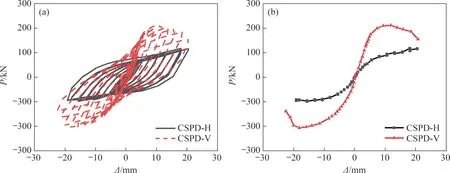
图4 试件滞回曲线与骨架曲线Fig.4 Hysteresis curve and skeleton curve of specimens

综合来看，对于人字形支撑框架结构，布置阻尼器后，地震作用导致的变形和损伤集中在阻尼器上。阻尼器主要承受水平方向的荷载，利用波形腹板的弹塑性变形，耗散地震能量，达到保护整体框架结构的目的。对于阻尼器试件CSPD-H与CSPD-V而言，试件CSPD-V拥有更高的抗侧承载力，因此更适合布置在支撑框架结构中。

1.3.2 有限元验证

利用ABAQUS 有限元软件，建立试件CSPDH与CSPD-V的有限元模型，并将有限元结果与试验结果进行对比。以材性试验中得到的钢材力学性能参数为依据，确定有限元模型中的本构参数。在有限元模型中，阻尼器的上、下端板采用C3D8R 实体单元；阻尼器的波形腹板和翼缘板采用S4R 壳单元；阻尼器的端板和波形腹板及各个构件之间采用绑定(Tie)的方式连接。不同试件的正面及侧面应力云图如图5 所示。由图5 可以看出：有限元模拟结果与试件的变形结果较符合，说明有限元模拟结果有一定的参考价值。

图5 不同试件的正面及侧面应力云图Fig.5 Stress cloud diagrams of the front and side of different specimens

试件CSPD-H 与CSPD-V 的滞回曲线及骨架曲线的试验结果和有限元结果的对比如图6所示。从滞回曲线来看，有限元模拟结果与试验结果吻合度较高，有限元模拟得到的滞回曲线比试验得到的滞回曲线的滞回环面积稍大。这是因为有限元软件的模拟结果较为理想化，而试验中的影响因素较多，如初始缺陷、加工与制作试件产生的误差等都会对试验结果产生影响。从骨架曲线来看，有限元模拟结果与试验结果曲线形状较为相似，骨架曲线均为S形，骨架曲线的走势基本一致。试件CSPD-H的承载力较低，而试件CSPD-V的承载力相对较高。这是因为当波形钢板竖向放置时，沿波形截面方向约束较强，波形钢板能够充分发挥其面外刚度大的优势；而波形钢板横向放置时，沿波形截面方向约束较小，波形钢板面外刚度大的优势未能充分发挥。结合以上分析来看，有限元模拟结果可以为后续阻尼器在人字形支撑框架结构中的应用提供参考。

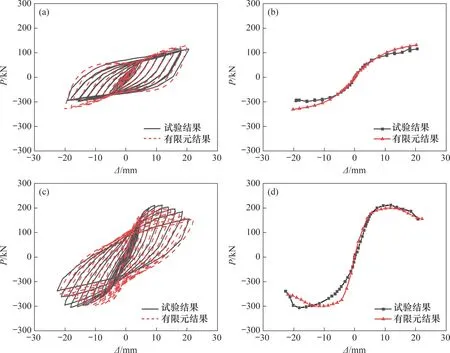
图6 试件滞回曲线及骨架曲线的试验结果和有限元结果对比Fig.6 Experimental result and finite element results of hysteresis curve and skeleton curve of specimens

2 带阻尼器的人字形支撑框架结构

2.1 框架结构的构造

人字形支撑框架结构的三维图如图7(a)所示。整体框架结构由框架柱、框架梁、阻尼器、支撑、连接件等组成，人字形支撑通过上、下连接件与框架相连，阻尼器布置于人字形支撑上，阻尼器的上端板与框架梁相连，各个部件连接组成附加阻尼器的人字形支撑框架结构。

框架结构的柱、梁和支撑均采用Q235 材质的H 型钢，框架柱的高×宽×腹板厚度×翼缘厚度为400 mm×400 mm×16 mm×16 mm；框架梁的高×宽×腹板厚度×翼缘厚度为400 mm×250 mm×12 mm×15 mm；为保证支撑拥有足够的抗侧刚度，不先于阻尼器发生破坏，人字形支撑的高×宽×腹板厚度×翼缘厚度为300 mm×300 mm×10 mm×12 mm；阻尼器的波形板厚度选为6 mm，框架结构尺寸如图7(b)所示。

图7 框架结构的构造Fig.7 Construction of frame structure

2.2 框架结构的有限元分析

2.2.1 有限元模型的建立

为了研究波形腹板阻尼器在人字形支撑框架结构中的抗侧性能，借助ABAQUS 有限元软件，建立有限元模型，如图8所示。框架柱、框架梁、支撑、阻尼器及各个部件之间采用绑定(Tie)连接，框架结构均采用C3D8R 实体单元，阻尼器的单元选择、本构参数、建模方法参考本文1.3.2 节阻尼器的有限元验证。根据“建筑消能减震技术规程”[17]，对框架结构的各部件采用双线性本构模型。

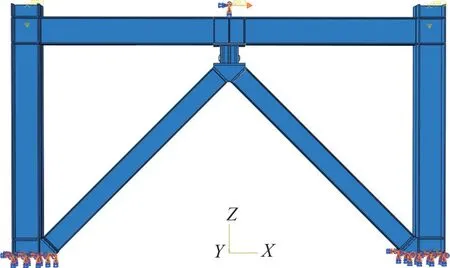
图8 有限元模型Fig.8 Finite element model

加载方式为低周往复加载，并采用位移控制的加载形式，一共加载10 圈，最大加载位移为66 mm。为了更真实地模拟框架结构的上部荷载，在左、右框架柱柱顶施加200 kN 的轴向力，循环荷载施加在耦合的参考点上，在水平方向施加往复作用力。

2.2.2 结果分析

通过有限元模拟得到不设置阻尼器的人字形支撑框架结构的应力云图，如图9(a)所示。由图9(a)可以看出：在水平往复荷载的作用下，不设置阻尼器的支撑框架结构的支撑及框架梁均产生了屈曲破坏，对框架结构的安全产生了威胁。设置阻尼器的支撑框架结构如图9(b)所示。由图9(b)可以看出：支撑框架结构中主要是阻尼器发生破坏，阻尼器能够发挥“保险丝”的作用，将结构的塑性变形和损伤集中于阻尼器的耗能腹板上，框架梁及支撑不先于阻尼器发生破坏，阻尼器能够有效保护结构的安全。

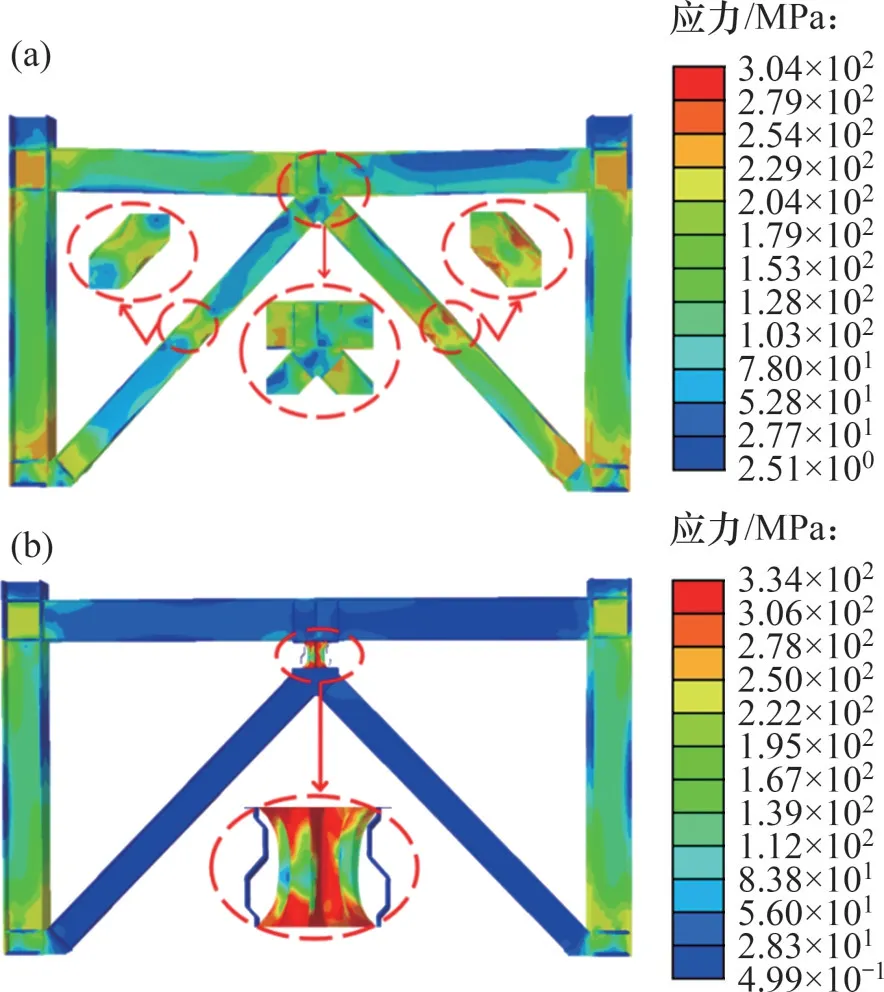
图9 支撑框架结构的应力云图Fig.9 Stress cloud diagram of braced frame structure

对于不设置阻尼器的支撑框架结构，支撑结构是抗震的第1道防线，主要依靠支撑的屈曲及变形来耗能，但支撑及框架梁破坏严重，框架梁的修复及更换较为困难，因此，以牺牲框架梁及支撑来耗能是不经济的，且会给建筑结构带来安全隐患。而对于设置阻尼器的支撑框架结构，阻尼器作为抗震的第1道防线，阻尼器破坏后更换较为方便，能够有效保护框架结构的安全。因此，在实际工程应用中，可在支撑框架结构中设置波形腹板阻尼器。

3 参数分析

改变框架结构的梁、柱截面尺寸以及阻尼器的波形腹板厚度，以便进一步研究设置波形腹板阻尼器人字形支撑框架结构的承载能力及耗能能力。为保证支撑结构拥有足够的强度，支撑结构的高×宽×腹板厚度×翼缘厚度仍然设置为300 mm×300 mm×10 mm×12 mm，阻尼器中只改变波形腹板的厚度。一共建立16 个有限元模型，模型中构件的截面尺寸如表1所示。

表1 构件的截面尺寸Table 1 Section dimensions of components

3.1 承载力

支撑框架结构的骨架曲线如图10 所示。由图10 可见：在保持框架结构的梁、柱截面尺寸不变的情况下，增加阻尼器的波形腹板厚度，能够提升支撑框架结构的承载力。这是因为增加波形腹板的厚度，能够保证阻尼器不会过早地发生破坏，因而框架结构的承载力会得到提升。在保持阻尼器的波形腹板厚度不变的情况下，增大框架结构的梁、柱截面尺寸，框架结构的承载力有所提升。这是因为波形腹板阻尼器人字形支撑框架结构为双重抗侧体系，阻尼器是框架结构抗震的第1道防线，阻尼器失效后，框架结构主要通过柱及梁的弯曲变形来耗能。

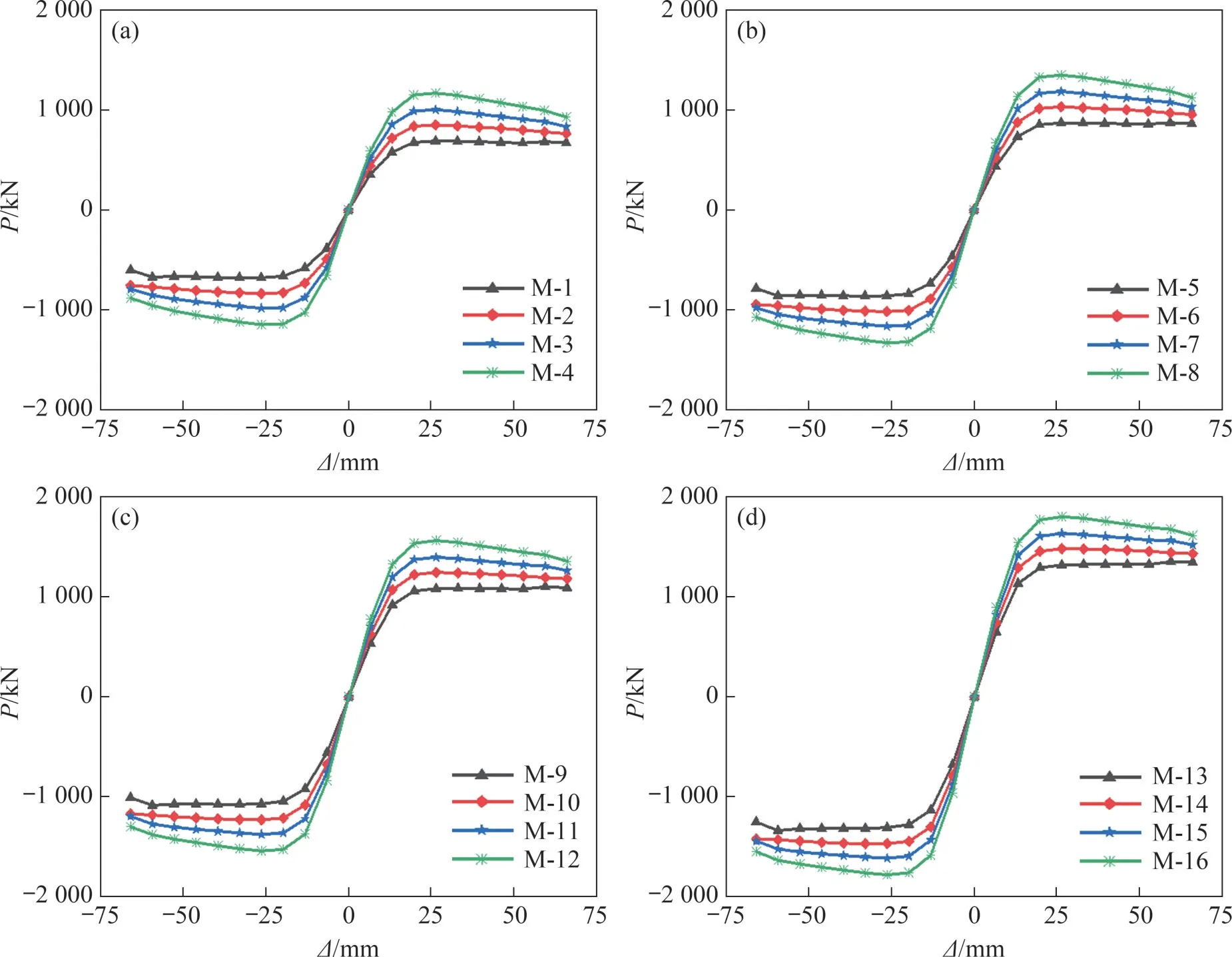
图10 支撑框架结构的骨架曲线Fig.10 Skeleton curves of braced frame structure

综合来看，波形腹板阻尼器人字形支撑框架结构的波形腹板应选择合适的厚度。若腹板太薄，则阻尼器容易过早失效；若腹板太厚，则会导致框架梁及支撑先于阻尼器破坏。

3.2 累计耗能

在滞回曲线中的加荷阶段，荷载-位移曲线下所包围的面积可以反映结构吸收的能量。单圈滞回环的面积即为结构的单圈耗能，单圈耗能叠加则为结构整体的累计耗能。结构的累计耗能玫瑰图如图11所示。由图11可知：增加阻尼器波形腹板厚度及增大梁、柱截面尺寸，结构的耗能能力均有所提升。M-1表现出较差的耗能能力，这是因为在水平荷载的作用下，阻尼器过早破坏，结构失去抗震的第1道防线，因而结构的承载力及耗能较差。M-16 表现出较好的耗能能力，这是因为阻尼器的波形腹板厚度适中，框架梁、柱抗侧刚度大，阻尼器能发挥较好的耗能作用。

图11 框架结构累计耗能玫瑰图Fig.11 Cumulative energy dissipation rose diagram of frame structure

4 抗侧性能

4.1 抗侧刚度

4.1.1 框架结构抗侧刚度

结构的抗侧刚度可由屈服荷载除以屈服位移计算得到，波形腹板阻尼器人字形支撑框架结构的抗侧刚度K则可以采用式(1)计算得到：

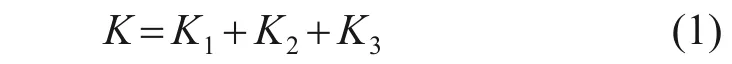
式中：K1为框架柱的抗侧刚度；K2为支撑机构的抗侧刚度；K3为阻尼器波形腹板的抗侧刚度。

在地震荷载作用下，波形腹板阻尼器发挥耗能作用，框架梁、柱仍处于弹性状态。框架柱的抗侧刚度，可采用D 值法计算，由于本文框架结构只有一层，因此不考虑修正系数的影响，结合力学知识可得到框架柱的抗侧刚度K1的表达式为

式中：E为材料的弹性模量；Ic为框架柱的截面惯性矩；Hc为框架柱的高度。

对于框架的支撑结构，可以将支撑简化为悬臂梁，由此可得支撑结构的抗侧刚度K2的表达式为

式中：Iz为支撑结构的截面惯性矩；Lz为支撑结构的长度；α为支撑与水平面的夹角。

4.1.2 阻尼器抗侧刚度

波形腹板阻尼器的抗侧刚度主要由耗能腹板提供，波形腹板为主要的耗能构件。图12 所示为波形腹板的抗侧刚度计算示意图。图12中：ɑ为波形腹板平波段长度；b为波形腹板斜波段长度；c为波形腹板的平直段长度；d为波形腹板半个波形水平投影距离；h为波形腹板的波幅；θ为波角(斜波段与中轴线的夹角)。

图12 波形板抗侧刚度计算示意图Fig.12 Calculation diagram of lateral stiffness of corrugated plate

波形板的抗侧刚度K3的表达式[18]如下：

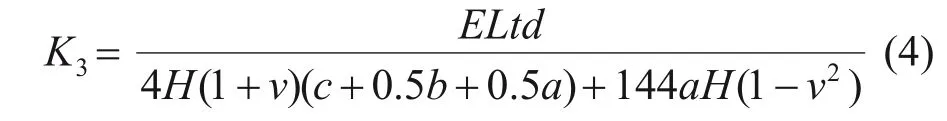
式中：ν为泊松比；t为波形板厚度；H为波形板高度；L为波形板宽度。

将式(2)～(4)代入式(1)，即可得到波形腹板阻尼器人字形支撑框架结构的抗侧刚度K：

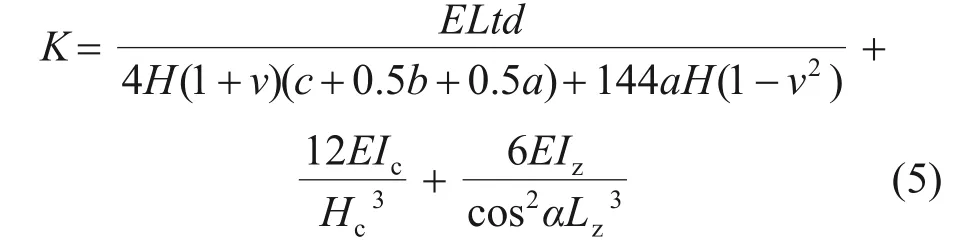
为了验证式(5)的准确性，将抗侧刚度计算值与模拟值对比，如表2所示。从表2可以看出，仅少数模型的抗侧刚度计算值与模拟值的相对误差绝对值大于10%，其余模型的抗侧刚度计算值与模拟值误差绝对值均小于10%。这是因为波形腹板阻尼器的腹板厚度较薄时，阻尼器过早破坏；波形腹板厚度较厚时，支撑提前屈曲，这些都会导致误差的产生。因此，在保证阻尼器腹板厚度适中的情况下，式(5)的计算结果具有一定的可靠性。

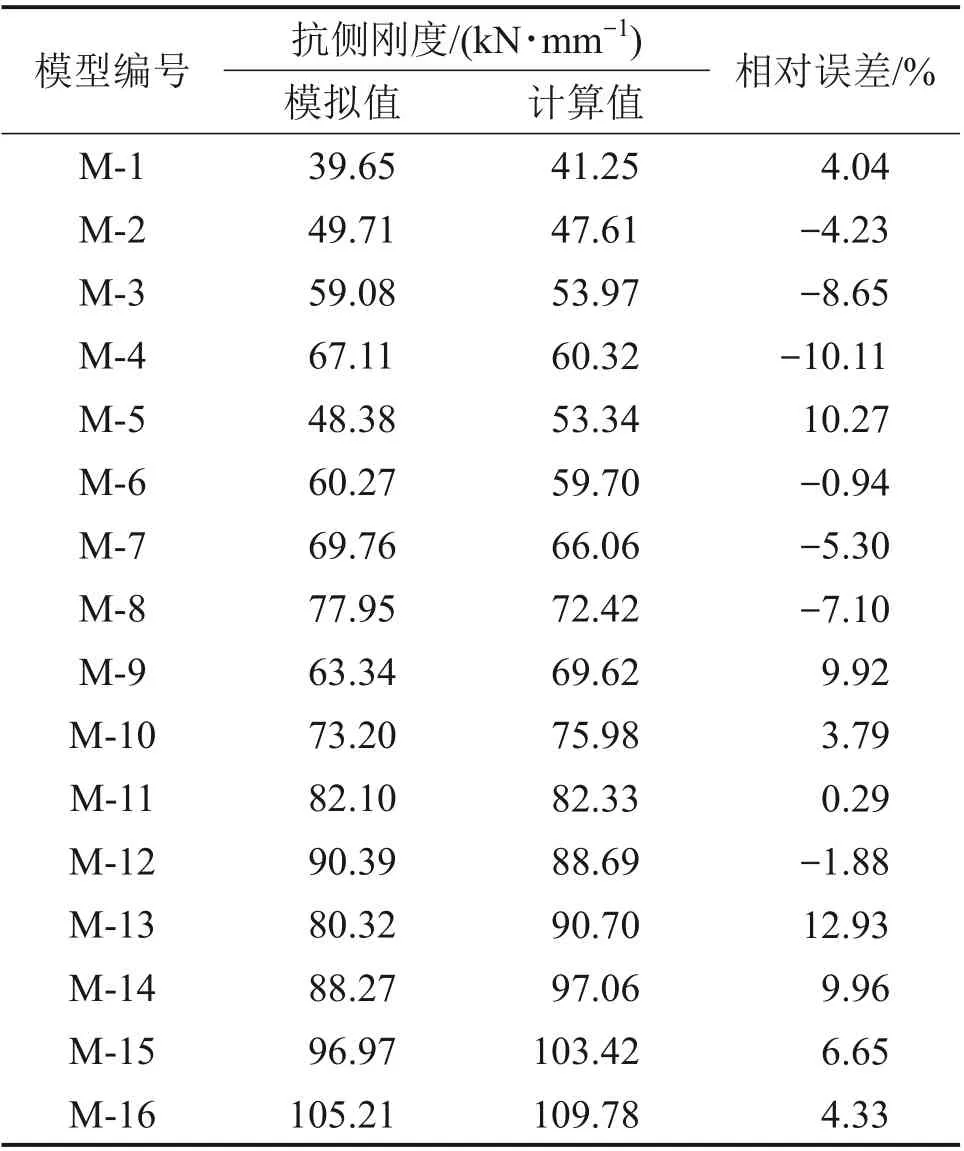
表2 框架结构抗侧刚度计算值与模拟值对比Table 2 Comparison between calculated and simulated values of lateral stiffness of frame structure

4.2 抗侧承载力

4.2.1 框架结构抗侧承载力

对于框架结构，假设框架柱及框架梁刚度足够大，阻尼器作为抗震的第1道防线，最先发生破坏。忽略框架梁的轴向变形，框架结构的抗侧力主要由阻尼器及框架柱提供。GB 50017—2003“钢结构设计标准”[19]规定，受弯构件的轴力及弯矩的关系式为

式中：φx为受压构件的稳定系数；Mx为所计算构件段范围内的最大弯矩；Wx为构件的截面抗弯模量；γx为截面塑性发展系数，取1.05；βmx为等效弯矩系数，可取1.0。

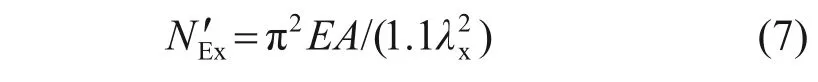
式中：λx为构件长细比。

在水平荷载作用下，纯框架结构的柱端弯矩Mpc的表达式为

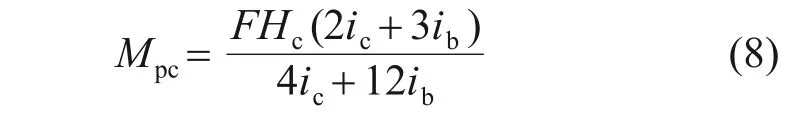
式中：F为水平荷载；Hc为框架柱的长度；ic为框架柱的线刚度，ic=EIc/Hc；ib为框架梁的线刚度，ib=EIb/Lb；Ib为梁的截面惯性矩。

令Mx=Mpc并代入式(6)中可得：

4.2.2 阻尼器抗侧承载力

波形腹板阻尼器主要依靠波形腹板屈曲变形耗能，因此阻尼器的抗侧承载力即为波形腹板提供的抗剪承载力。波形腹板阻尼器的受力简图如图13所示。图13中，Fd为波形腹板阻尼器所受水平力；Vd为波形腹板阻尼器抗侧承载力。

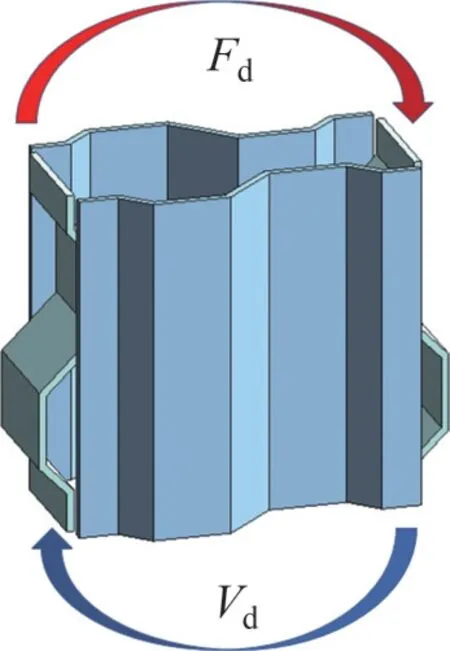
图13 波形腹板阻尼器受力简图Fig.13 Stress diagram of damper of corrugated web

本文取单片波形板进行研究，阻尼器翼缘板对承载力贡献较小，因此可以忽略翼缘板的承载力影响。根据T/CECS 624—2019“波形钢板组合结构技术规程”[20]，单片波形钢板的承载力V计算式为

式中：φs为单片波形板的受剪稳定系数；H为波形板的平直边长度；τy为剪切屈服应力，由Mises 屈服准则确定，其计算式为

波形板的稳定系数φs与正则化高厚比λs相关，本文结合有限元算例，拟合得到φs与λs的关系：

式中：Vcr为波形钢板受剪弹性屈曲荷载。

波形腹板阻尼器的2 片耗能腹板呈正对称分布，由此可得出波形腹板阻尼器的抗侧承载力Vd为

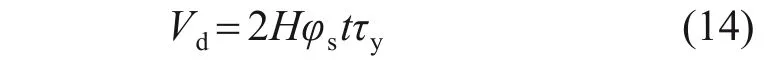
波形腹板阻尼器人字形支撑框架结构的受力简图如图14 所示。对于整体的支撑框架结构，支撑结构为阻尼器提供侧向约束，忽略框架梁的轴向变形，则波形腹板阻尼器的抗侧承载力为阻尼器的承载力与框架柱的承载力之和。根据叠加原理，波形腹板阻尼器的抗侧承载力Ps的表达式为

图14 支撑框架结构受力简图Fig.14 Stress diagram of braced frame structure

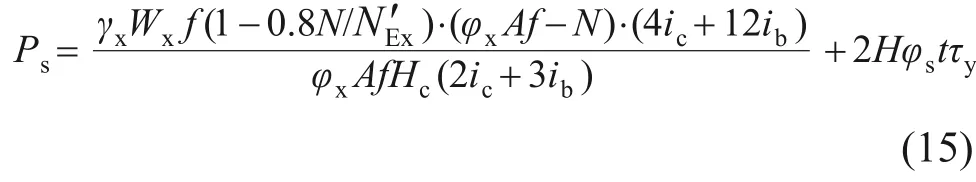
为了进一步验证式(15)的可靠性，将式(15)所得计算值与有限元模拟值对比，如表3所示。

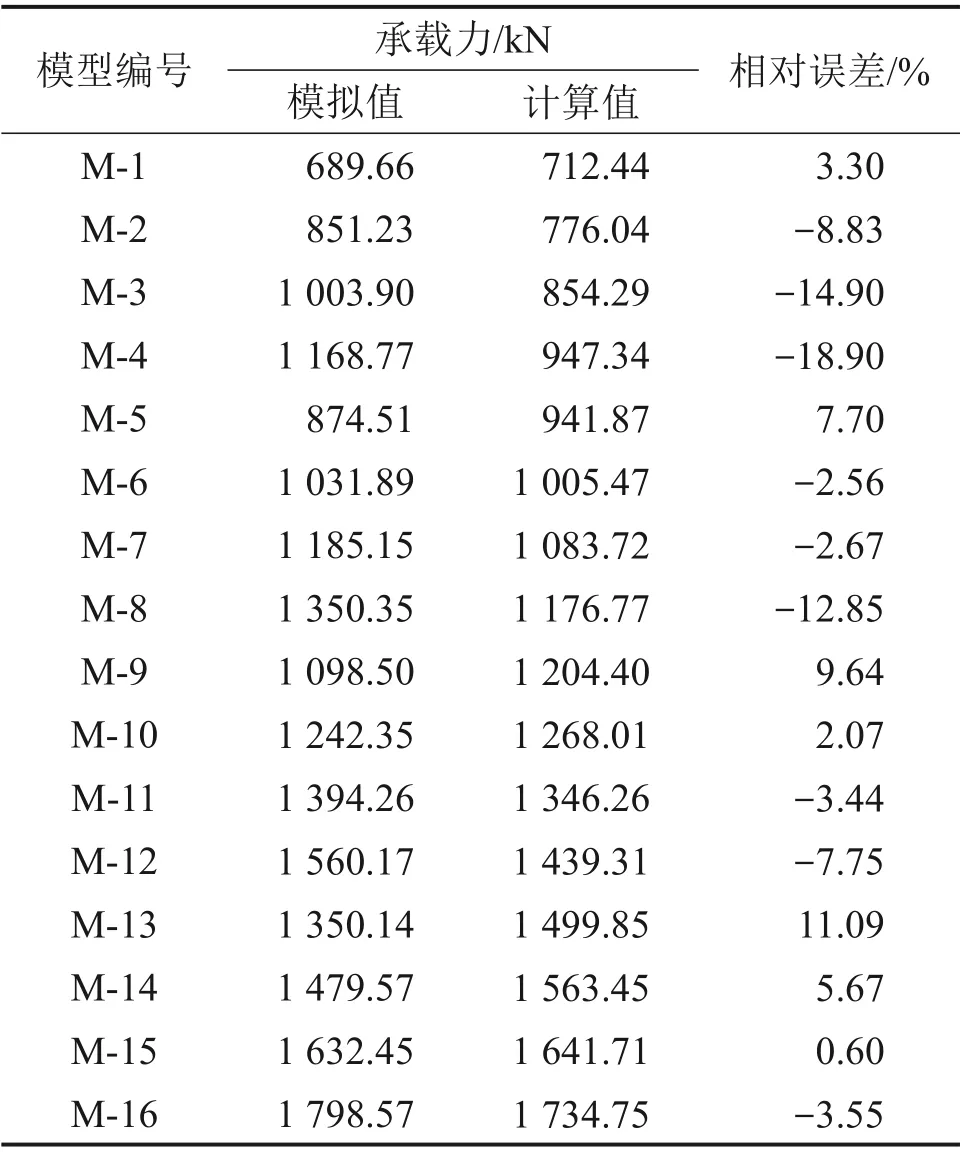
表3 框架结构承载力计算值与模拟值对比Table 3 Comparison between calculated and simulated values of bearing capacity of frame structures

从表3 可以看出：除了模型M-3，M-4 及M-8外，其余模型中承载力计算值与模拟值的相对误差绝对值均小于10%。这是因为模型M-3，M-4及M-8 阻尼器波形腹板厚度较大，而梁、柱强度不够，阻尼器未能充分发挥耗能作用，因此承载力理论计算值偏小，相对误差较大。在实际工程应用中，应保证框架梁、柱拥有足够的抗侧刚度，才能充分发挥阻尼器的耗能能力。本文所提承载力计算公式(式(15))具有一定的参考价值，可以用来估算波形腹板阻尼器人字形支撑框架结构的抗侧承载力。