丢番图恒等式在高中数学创新题中的应用
2022-08-28北京市顺义牛栏山第一中学李启超刘爱军邮编101300
北京市顺义牛栏山第一中学 李启超 刘爱军 (邮编:101300)
丢番图恒等式表明,如果两个正整数分别为两个平方数之和,那么这两个正整数的乘积也能写成两个平方数之和,即:
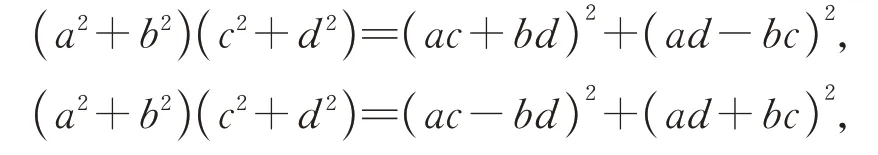
其中a、b、c、d可以取任意实数.
这个恒等式最早可以追溯到公元3 世纪丢番图(Diophantus)的著作《算术》中[1].公元7 世纪,婆罗摩笈多(Brahmagupta)把这个恒等式推广到更一般的情形(我们仍称之为丢番图恒等式):
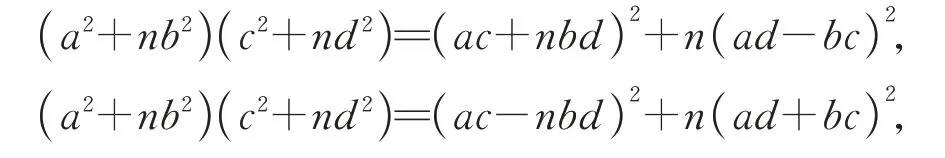
其中a、b、c、d和n可以取任意实数,通过两边展开,容易验证上面恒等式成立.当n=-1 时,有:
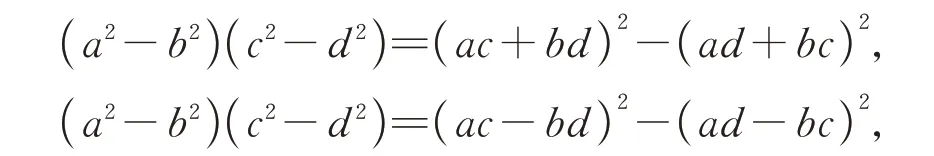
这些恒等式形式简单结构优美,在数学史上曾启发了一系列重要发现.它们不仅在初等数论和多项式问题中有重要应用,还经常出现在各类高中数学试题中.以下详细介绍丢番图恒等式在两类创新题中的应用
1 在集合问题和代数式变形问题中的应用
例1设A是两个整数平方和的集合,即A={x|x=m2+n2,m、n∈Z}.
(1)证明:若s、t∈A,则st∈A;
(2)证明:若s、t∈A,t≠0,则,其中p、q是有理数.
分析本题要求验证集合A具有乘法封闭性,即两个平方和的乘积仍然可以写成平方和的形式.要证st∈A,只需借助丢番图恒等式证明其是两个整式的平方和即可.

即st是两个整数的平方和,所以st∈A.
(2)由于s、t∈A,由(1)可知,st∈A.于是可以设st=m2+n2,m、n是整数.又因为t≠0,因此
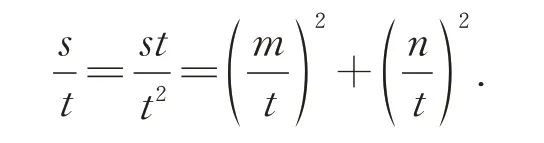
例2设A是两个整数平方差的集合,即A={x|x=m2-n2,m、n∈Z}.
(1)证明:若s、t∈A,则st∈A;
(2)证明:若s、t∈A,t≠0,则,其中p、q是有理数.
分析与上一个例题类似,要证st∈A,只需借助丢番图恒等式证明其是两个整式的平方差即可.
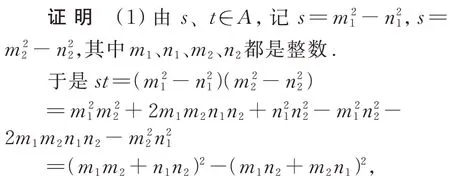
即st是两个整数的平方差,所以st∈A.
(2)由于s、t∈A,由(1)可知,st∈A.于是可以设st=m2-n2,m、n是整数.
又因为t≠0,因此
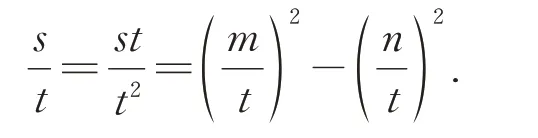
例3已知a2+b2=1,c2+d2=1,ac+bd=0.求证:a2+c2=1,b2+d2=1,ab+cd=0.
分析这道题有明显的线性代数背景:如果2×2 矩阵中,两个行向量是单位正交向量,则这个矩阵是正交矩阵,从而两个列向量也是单位正交向量.本题的常规方法是三角换元,或者比值代换,其实借助丢番图恒等式也可解决.
证明根据丢番图恒等式(a2+b2)(c2+d2)=(ac+bd)2+(ad-bc)2,可知1=0+(ad-bc)2,从而ad-bc=±1.
(1)当ad-bc=1 时,将视为关于(c,d)的二元一次方程组,
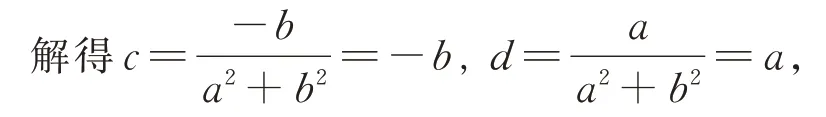
代回条件a2+b2=1,c2+d2=1,ac+bd=0,可得a2+c2=1,b2+d2=1,ab+cd=0;
(2)当ad-bc=-1 时,将视为关于(c,d)的二元一次方程组,

代回条件a2+b2=1,c2+d2=1,ac+bd=0,可得a2+c2=1,b2+d2=1,ab+cd=0.证毕.
2 在高中数学联赛试题中的应用
丢番图恒等式还可以用于解决一些与平方和(差)有关的竞赛最值问题,试看几例:
例4(2021年全国高中数学联赛A1 卷一试第8题) 已知正实数x、y满足如下条件:存在a∈[0,x],b∈[0,y],使得a2+y2=2,b2+x2=1,ax+by=1.则x+y的最大值为______.
分析题目给出的等式条件中有好几处平方和的结构,这启发我们不妨试试丢番图恒等式.
解答根据丢番图恒等式(a2+y2)(x2+b2)=(ax+by)2+(ab-xy)2,可知(ab-xy)2=1.又因为x≥a≥0,y≥b≥0,可知xy-ab=1.

说明以上题目,主试委员会提供的标准答案是使用三角换元法.上面借助丢番图恒等式,解题过程更加简洁.
例5(2017年全国高中数学联赛一试第10题 第(1)问) 设复数z1、z2满足Re(z1)>0,Re(z2)>0,且(其中Re(z)表示复数z的实部).求Re(z1z2)的最小值.
分析将复数z1、z2写成实数分量形式,容易发现条件Re(z1)>0,Re(z2)>0,且等价于复数z1、z2对应的点在双曲线x2-y2=2 的右半支上.接下来,根据丢番图恒等式不难解决问题.

完全类似的方法,还可以解决下面的2006年北京市高考理科数学解析几何问题,将其视为例5 的变式练习题.
例6已知点M(-2,0)、N(2,0),动点P满足条件.记动点P的轨迹为W.
(1)求W的方程;
(2)若A、B是W上的不同两点,O是坐标原点,求的最小值.
解答(1)根据双曲线定义,可知动点P的轨迹为双曲线的右半支,轨迹W的方程为x2-y2=2(x>0);

说明这是一道解析几何问题,常规解法是先联立直线AB和曲线W的方程,然后借助韦达定理将写成关于直线AB斜率和截距的函数再求最值.以上解法借助推广的丢番图恒等式,形式紧凑,思路清晰,而且不必分类讨论直线AB斜率不存在的特殊情形.
3 总结
丢番图恒等式结构简洁,应用广泛.有意识地借助丢番图恒等式解决问题,可以提高学生的代数运算能力和知识迁移能力.对于学有余力的高中生,我们不妨在选修课上适当介绍这类恒等式在各类问题中的应用.
