一种面向全空域覆盖阵列的和差比幅测角跟踪方法*

谢 伟，陈 颖，杨 龙，王 娜，袁 田，王 茗

(1.中国西南电子技术研究所，成都 610036；2.中国人民解放军63760部队，南宁 530009)

0 引 言

在卫星通信和测控通信等领域，随着国内外关于全空域相控阵系统的研究与应用[1-2]，具有全空域覆盖能力的相控阵系统大有替代传统抛物面系统的趋势。

对于相控阵的测角，常用的方法包括CAPON算法、子空间类算法[3]以及单脉冲测角方法[4-6]等。CAPON算法和子空间类算法虽然具备超分辨特性，但其计算过程复杂。相对而言，单脉冲类方法利用目标辐射信号的单个采样快拍即可完成测角，对目标信号起伏不敏感，且原理简单、实现复杂度低，在实际工程中应用最为广泛。

单脉冲技术主要包括和差比幅[7]以及和差比相[8]两类方法，且均已广泛应用于相控阵系统。对于平面阵列，单脉冲技术的应用已趋于成熟，但对于具备全空域覆盖能力的相控阵系统，仅有和差比相方法成功进行了应用扩展[2,9]，尚未见和差比幅方法在全空域系统中成功应用的报道。

受遮挡效应的影响，全空域系统在使用过程中需首先根据波束指向进行阵元激活状态的计算[2]，这导致在不同的波束指向时阵列具有不同的激活状态。与此同时，和差比相方法的应用需要将激活阵元进行区域划分，且各区域增益的一致性和等效相位中心的对称性直接决定了和差比相方法的性能。在子阵化、多面体拼接等工程化因素的约束下，全空域系统难以保证增益一致性和区域的对称性，进而对适用阵列具有一定的限制。

和差比幅方法从不同波束接收信号的幅度中估计目标偏离等强轴方向的程度。显然，和差比幅方法同样适用于全空域系统，且其性能主要由幅度响应或波束方向图决定，对阵元分布并没有对称性要求，因此可以作为和差比相方法的有效补充。

为将和差比幅方法扩展到全空域系统，本文给出了测向辅助波束的指向计算方法和子阵级多波束形成的计算方法，以降低多波束形成的计算和实现复杂度。仿真结果验证了所提方法的有效性和优越性。

1 信号模型

假设一个窄带阵列系统由M个子阵组成，子阵内的阵元个数为L，则可将阵列指向方向p∈3×1的导向矢量写作b(p)=[b1(p),…,bM(p)]T，其中，(·)T表示转置，bm(p)=[bm1(p),…,bmL(p)]T表示子阵m指向方向p的导向矢量。若将阵元坐标和阵列波长分别表示为{dml∈3×1}m,l和λ，则有

(1)

式中：vml(p)和aml(p)分别表示子阵m中阵元l在方向p处的幅度和相位响应。若考虑子阵均是由均匀平面阵组成，则在子阵内不同阵元在同一方向的幅度响应可假设一致，也即

vm(p)≐vm1(p)=…=vmL(p),m=1,2,…M。

(2)

ym(t)=vm(pt)am(pt)s(t)+nm(t)。

(3)

式中：am(p)=[am1(p),…,amL(p)]T，pt∈3×1表示目标信号的入射方向向量(对应球坐标系下方向可假定为方位角θt和俯仰角φt)，s(t)∈1×1表示目标信号传输到坐标原点处的信号波形，nm(t)∈L×1表示子阵m接收到的噪声矢量。对于数字相控阵系统而言，所有测角算法都是基于采样得到的IQ信号{y(t)}t进行处理。

式(3)给出了阵列信号的一般性接收模型。该模型可以兼容实际工程中的绝大部分阵列，例如，对于小规模全空域阵列，阵面未进行子阵化分，则只需将上述参数L置1即可；而对于大规模共形阵(包括平面等常规阵列)，为了工程实现方便，大都采用子阵化设计、多级波束形成的架构[1]。

2 测向辅助波束的指向计算

比幅单脉冲技术需要至少形成4个指向不同的测向辅助波束，对于辅助波束的波束指向配置，可采用图1所示方案(其他配置方案可参见文献[7-8])。

图1 波束指向配置示意图

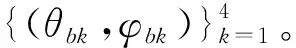
对于抛物面而言，pb1～pb4与pb的夹角关系固定且相等，而对于相控阵系统，各波束指向与等强轴方向的夹角可以由不同指向条件下横纵向的实际波束宽度而进行灵活配置。

假定横纵向辅助波束的偏角已确定(参见后文讨论)，可在辅助坐标系下对测向辅助波束的具体角度进行计算，再通过辅助坐标系与阵面坐标系之间的关系计算阵面坐标系下测向辅助波束的具体指向。该辅助右手坐标系可选择如下：坐标原点与阵面坐标系重合，x0轴指向等强轴方向，y0轴指向横向方向，如图2所示。由横纵向和等强轴方向相互正交的关系可知，z0轴方向纵向方向重合。

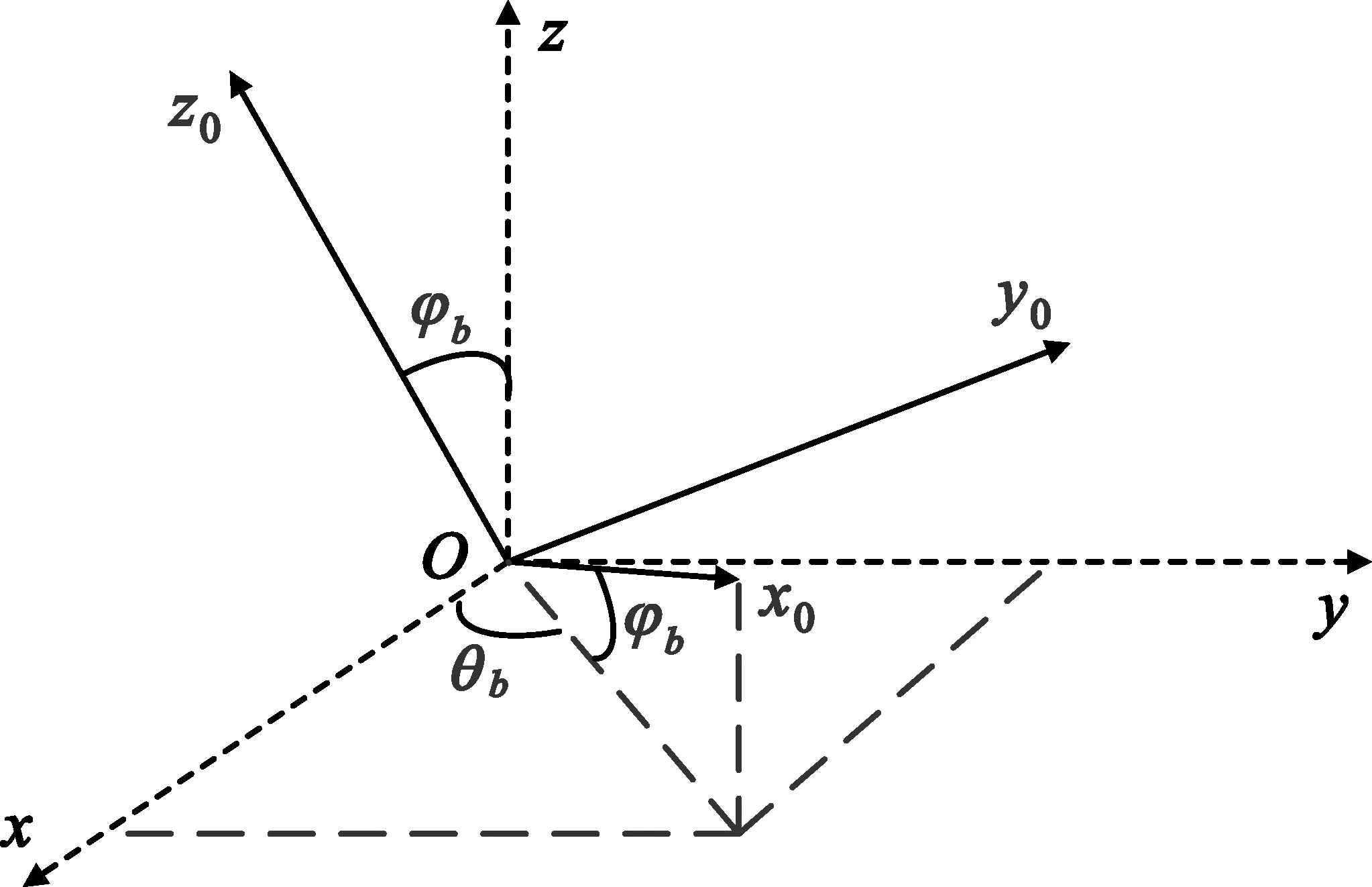
图2 阵面坐标系Oxyz和辅助坐标系Ox0y0z0关系示意图

由定义可知，横向同时垂直于等强轴方向和阵面坐标系中的z轴，因此横向一定在阵面坐标系中的xOy平面内，且辅助坐标系的z轴、阵面坐标系的z轴以及等强轴方向一定共面。

根据两个坐标系之间的几何关系，可以通过两次坐标旋转实现两个坐标系的转换。以辅助坐标系到阵面坐标系的旋转为例，可首先将Ox0y0z0坐标系绕y0轴逆时针旋转φb，再绕z0轴顺时针旋转θb即可实现两坐标系的重合，对应旋转矩阵可表示为

(4)

根据等强轴方向pb、横向(同时与pb和俯仰向相垂直的方向)波束宽度θh3dB、纵向(俯仰向)波束宽度θz3dB，可以直接确定在辅助坐标系下，测向辅助波束1～4的方向分别为(0,-qθz3dB)、(qθh3dB,0)、(0,qθz3dB)和(-qθh3dB,0)，其中，q是一个比例常数，表示辅助波束相对等强轴指偏角与3 dB波束宽度的比值，q越大，指偏越大，S曲线(即差和比)越陡峭，但波束接收信号的增益损失越大，且由于整个比幅测角的表达式是基于对方向图函数进行高斯拟合的假设下得到，且利用到一阶泰勒近似(参见第4节)，因此方向图仅在主瓣内的拟合误差较小，综合仿真分析结论(参见仿真验证小节)，建议q的取值在0.45左右。

利用辅助坐标系与阵面坐标系之间的转换关系，可以得到

pb1=Γp0(0,-qθz3dB),pb3=Γp0(0,qθz3dB)，

(5)

pb2=Γp0(qθh3dB,0),pb4=Γp0(-qθh3dB,0)。

(6)

式中：p0(θ,φ)=[cosθcosφ,sinθcosφ,sinφ]T。至此，利用式(5)和式(6)并结合实际波束宽度，以及式(4)的两坐标系的转换矩阵便可计算得到测向辅助波束的具体指向。

3 子阵级多波束形成

由于和差比幅方法需要形成4个测向辅助波束，对于大规模阵列，可采用文献[8]所述的子阵级多波束形成方法，以降低资源消耗。

子阵级波束形成分为子阵内加权合成和子阵间加权合成两级。在子阵内，各子阵均指向等强轴方向pb，子阵m的合成数据可表示为(此处忽略了噪声项)：

(7)

在子阵间，欲使全阵合成波束指向辅助波束方向pbk，子阵m的加权值wbkm可表示为[10]

(8)

进而，全阵合成指向第k个辅助波束方向pbk的波束数据zbk(t)以及对应幅度ubk(t)分别为

(9)

ubk(t)=|zbk(t)|。

(10)

4 和差比幅测角

基于相控阵的和差比幅测角在横纵两个方向上的处理完全一致，因此可以首先以一维测角(纵向)的情况对测角原理进行讨论。

考虑图3所示一维测向场景，图中φt表示目标方向；φd、φ1、φ3分别表示等强轴方向、测向辅助波束1和3的指向且φd=φb-φ1=φ3-φb；Δz=φt-φb表示目标方向与等强轴方向的夹角，也即待估计的纵向指向角误差。

图3 一维比幅和差测角示意图

在图3所示场景下，两波束在接收合成信号的幅度可分别表示为(以单快拍数据进行说明)

ub3=P0Fz(φ3-φt)=P0Fz(φd-Δz)，

(11)

ub1=P0Fz(φt-φ1)=P0Fz(φd+Δz)。

(12)

式中：P0是由目标信号发射EIRP、距离衰落和G/T值等因素决定的比例系数，Fz(·)表示纵向的波束幅度方向图。

对两个波束接收信号做和差计算，可以得到纵向和信号uzΣ以及差信号uzΔ分别为

uzΣ=ub3+ub1，

(13)

uzΔ=ub3-ub1。

(14)

方向图函数可用高斯函数对方向图函数进行拟合，其表达式如下：

(15)

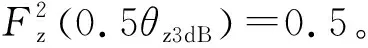
考虑误差Δz是一个较小的数，则可将Fz(φd-Δz)和Fz(φd+Δz)在φd进行泰勒展开，近似后得到

(16)

(17)

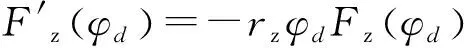
uzΣ=2P0Fz(φd)，uzΔ=2P0rzφdFz(φd)Δz。

(18)

进而，纵向差波束信号与和波束信号的比值

(19)

以上结果说明，差和信号比值在一定范围内是角误差的线性函数，斜率为ρz。

对于横向，类似于纵向的推导，可以得到横向和信号uhΣ以及差信号uhΔ分别为

uhΣ=ub2+ub4，

(20)

uhΔ=ub2-ub4，

(21)

以及横向差和比值

(22)

(23)

式中：Δh表示横向角误差，ρh表示横向比例系数，θd表示横向波束指向相对于等强轴的偏角。

基于式(9)、式(22)和式(23)，可以得到横纵向误差估计。与辅助波束指向的计算类似，方位向角误差的估计并不能直接从横向角误差直接得到，但横纵向误差刚好就是在辅助坐标系下的方位角和俯仰角，因此在阵面坐标系下的目标方向可直接通过以下坐标旋转的方式得到

pt=Γp0(Δh,Δz)。

(24)

式中：向量函数p0(Δh,Δz)与式(5)中的定义一致。

5 角度滤波与跟踪

整个测角算法的推导过程中利用高斯函数对方向图函数进行拟合，在目标方向先验误差较大或方向图函数不够对称的条件下拟合误差较大。同时，波束宽度会随着波束指向的变化而变化，而实际工程中不可能将每个指向的波束宽度进行测量。

高斯拟合误差和波束宽度误差均会引入误差到比例系数ρh和ρz当中，进而恶化比幅测角的性能。由于比例系数是由波束宽度和指偏角决定的正实数，因此可将误差建模为乘性误差。

为提升在乘性误差的条件下的测角精度，可以采用迭代多次实施测角；也可以采用滤波的方式，通过环路参数与波束指向的自适应调整，实现目标的角度的闭环测量与跟踪。常用的滤波方式包括环路滤波以及卡尔曼滤波，其中环路滤波器以其物理含义明确、实现简单、性能优越等特点，已在包括角跟踪系统在内的众多领域中得到了广泛的应用。

基于和差比相与和差比幅的环路滤波具有相同的原理。现有角跟踪方案包括角度跟踪(对方位角和俯仰角进行滤波)和三轴跟踪(对直角坐标系下的指向向量进行跟踪)两类，其中角度跟踪会涉及到过顶条件下目标方位角的突变和俯仰角角速度的突变问题。

文献[2]提出的三轴跟踪方法在估计到横纵向角误差后，首先计算方位向和俯仰向角误差，然后在此基础之上计算指向误差向量，最后再对目标方向向量进行环路滤波。在方位向角误差的计算过程中采用了一个近似的表达式，该表达式在低俯仰角处的近似程度很高，但在高俯仰角处其近似误差不可忽略。为避免该问题，可直接利用式(24)得到的目标指向向量估计结果pt，将其减去等强轴方向pb，即可得到指向误差向量Δp：

Δp=pt-pb。

(25)

再利用pb和Δp进行环路滤波，便可实现对目标在下一个时刻方向的预测，进而根据预测结果调整波束指向pb，再进行指向误差向量Δp计算、滤波以及其他迭代操作，直到跟踪稳定(对于静止目标)或者目标消失为止(对于动目标)。环路滤波技术已趋于成熟，其具体原理此处不做赘述，可参见文献[2]和[9]。

现将本文讨论方法的计算过程汇总如下：

Step1 离线确定横纵向波束宽度(θh3dB、θz3dB)以及辅助波束的指偏角θd和φd(对于不同指向条件下，波束宽度变化大的阵列，可存储多个波束宽度值)；确定目标方向向量pb。

Step2 利用式(5)和式(6)计算辅助波束指向pb1～pb4。

Step3 多波束形成，利用式(9)和式(10)计算各辅助波束接收信号幅度ub1(t)～ub4(t)。

Step4 计算横纵向和信号uhΣ、uzΣ与差信号uhΔ、uzΔ，计算方式参见式(13)、式(14)和式(20)、式(21)。

Step5 利用式(19)和(22)、(23)计算横纵向比例系数ρh、ρz和差和比Gh、Gz。

Step6 计算横纵向角误差估计值：Δh=Gh/ρh，Δz=Gz/ρz(对于多快拍情况，角误差估计值做平均即可)。

Step7 利用式(24)和式(25)计算目标方向误差向量Δp。

Step8 将目标方向误差向量进行环路滤波，并将滤波结果更新目标方向向量pb，再重复执行Step 2～ 8，直至目标消失(动目标)或收敛(静止目标)。

在计算量方面，提出方法需要进行4次加权合成，得到4个波束。采用阵元级多波束形成和子阵级多波束形成的计算复杂度分别为O(4MLT)和O(ML(T+1)+4MT)，其中T表示采样快拍数。在测角过程中的其他步骤中，主要的计算量在于Step 5中的差和比计算和Step 6中的角误差估计，其计算复杂度为O(4T)，其余步骤中，辅助波束指向计算(需56个乘加运算)、比例系数计算(可离线计算)、方向误差向量计算(需11个乘加运算)均与快拍数无关。总的计算复杂度约为O((5ML+4M+4)T+ML+67)。

6 仿真验证

本节主要从差零深、指偏角影响、固定目标测角和运动目标角跟踪四个方面对比幅单脉冲测角方法进行仿真分析，为保证分析结果在实际工程中应用的合理性，仿真中均考虑了阵元幅度误差(-0.5～0.5 dB均匀分布)和相位误差(-20°～20°均匀分布)。

考虑一个由26个面组成(足球32面体去掉6个最低俯仰角处的面)的阵列，该阵列包含正5边形子阵11个，每个子阵由16个阵元组成，正6边形子阵15个，每个子阵由19个阵元组成，共计461个阵元。天线频率考虑为2 GHz，阵列在x、y、z方向的孔径分别约为1.5 m、1.5 m和1.2 m。在具体布阵方面，两种类型的子阵内部阵元坐标分布分别一致，对于正6边形子阵，阵元间距均为0.75λ；对于正5边形子阵，阵元间距在0.67～0.78λ之间，同时考虑单阵元的波束宽度为100°。整个阵面的子阵划分以及阵元位置如图4所示。

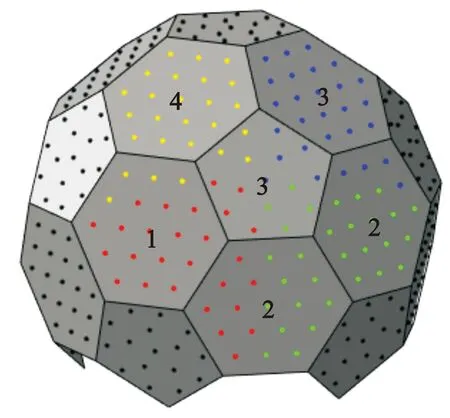
图4 球面阵子阵划分以及阵元坐标示意图

为对比幅和比相两种方法的差方向图进行对比，需要首先对阵列进行激活与区域划分。本文以波束指向与阵元法向夹角为60°为条件进行激活判断，同时将激活阵元进行横纵向区域划分，可得激活和区域划分结果如图4所示，图中红、绿、蓝、黄四种颜色分别标识出了在波束指向(72°,26.6°)(刚好是中心正五边形子阵的法线方向)时的区域1～4。

图5给出了基于图4区域划分方式得到的和差差波束方向图，其中子阵级区域划分采用了图4中数字编号的划分方式，子阵化区域划分可简化系统的实现复杂度，但其对称性已经被严重破坏。需注意，图4展示条件在阵元级区域划分时对称性良好，但若改变波束指向，在上述激活规则下同样无法保证区域间的对称性。

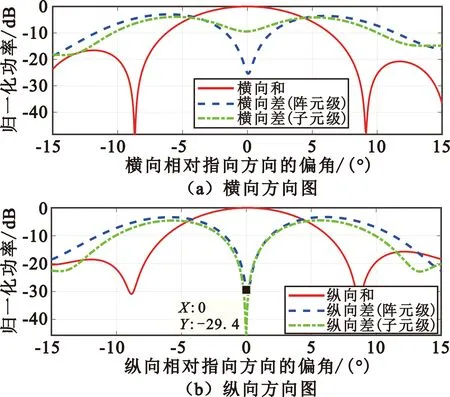
图5 比相单脉冲方法的和差波束方向图

由图5可以看到，阵元级区域划分后差零深均在30 dB以内，子阵级划分后纵向差零深达到了43 dB，但横向差零深恶化十分严重。

根据图5中的和波束得到横纵向波束宽度均为7.4°。图6给出了q=0.45条件下(波束指偏角均为3.3°)横纵向指偏波束以及差波束曲线，其中辅助波束的波束形成采用了子阵级波束形成方法。

图6 比幅单脉冲方法辅助波束以及差波束方向图

由图6可以看到，子阵级波束指向与设置值出现了约0.5°的指向偏差和约0.3 dB的增益损失。其原因在于子阵级波束形成中，子阵的波束指向固定且偏离于辅助波束指向，而合成波束由子阵波束和阵因子的乘积决定，由此带来最大增益与设置方向的偏差与增益损失(在子阵数量更多时，该损失可以降低)。除此之外，比幅方法展现出了优越的差波束性能，差零深均达到50 dB。

图7考察了式(19)和式(22)、(23)中差和比Gz以及Gh与角误差的关系，以及利用差和比与比例系数ρz和ρh计算角误差的拟合误差。由比例系数ρz和ρh的表达式可知，q越大，比例系数越大，因此差和比仅给出了q取值0.45的曲线；拟合误差的子图中给出了q分别取0.15、0.3、0.45、0.6和0.75的情况。

图7 理想与实际S曲线/拟合误差对比图

从图7可以看到S曲线在±5°区间内基本呈现线性的的关系，与理想曲线重合度较高。同时拟合误差曲线表明，近似线性的区域随着q的增加而减小。若且q取值太小(取值0.15或0.3)或太大(取值0.75)，在近似线性的区间内误差波动也较大，且在q取值太小时误差曲线有个明显上翘的现象。综合考虑，可将q取值为0.45～0.6。考虑到q越大增益损失越大，因此建议q取0.45即可，但具体取值应根据具体应用场景分析决定。

由图7仿真结论可知，受模型误差影响，和差比幅方法的单次测角具有一定偏差。同时由于模型误差属于乘性误差，测角偏差可以通过扫描、迭代闭环求解或环路滤波的方式解决。其中，后两类方法均属于闭环处理的方法，但迭代闭环求解仅适合于静态目标场景，而环路滤波对静态和动态目标均适用。因此，此处仅以基于环路滤波的动态目标跟踪为例进行性能验证。

考虑一个1 000 km高度圆轨道卫星的过顶场景，目标从俯仰角60°上升，过顶后下降到另一个方向的60°，其中最高俯仰角到达89.6°。为模拟实际工作场景，考虑波束指向更新周期50 ms，每个指向更新时刻用于测角的采样快拍数为512个点，阵元在其法向与波束指向夹角60°以内时激活。环路滤波采用二阶环路滤波器，环路带宽设置为2 Hz。仿真中，将横纵向波束宽度和辅助波束指偏角分别固定为7°和3.15°(q=0.45)，信号考虑为码速率为1 Mb/s的BPSK信号，成形因子0.5，初始时刻波束指向相对于真实目标方向的方位、俯仰向误差分别为-3°和-3°，合成后信号的信噪比设置为10 dB。

图8在给出目标真实方位和俯仰角的同时也给出了利用本文测角方法结合二阶环路器的跟踪结果，图9给出了测角误差曲线。作为对比，同时对和差比相方法进行了仿真，但对于子阵级和差比相以及阵元级和差比相方法，均无法收敛。

图8 目标跟踪角度和估计角度曲线

图9 目标测角跟踪误差曲线

从图8和图9可以看到，在实验条件下，比幅辅助以二阶环路的测角跟踪方法在高仰角处也能得到很好的跟踪性能，约1 s即可实现收敛，收敛后夹角误差的均方根误差(Root Mean Square Error,RMSE)约为0.07°。

图10给出了测角RMSE随信噪比的变化情况，其中，RMSE曲线由200次独立仿真结果统计得到，其余条件与图9仿真条件一致。

图10 目标测角跟踪误差曲线

从图10可以看到，在合成后信噪比-10～10 dB的区间内，RMSE随SNR呈近似线性的关系，而在大于10 dB条件下，RMSE减小程度不再明显。同时，在SNR大于-5 dB时即可实现0.1倍波束宽度的测角性能，且在高SNR(大于10 dB)条件下，夹角均方根误差达到0.07°。

7 结 论

本文研究了和差比幅方法在全空域阵列系统中的扩展，解决了测向辅助波束的指向计算问题，提出了一种基于高斯拟合的和差比幅测角方法，优化了角度滤波实现过程中角误差向量的估计方法，并通过仿真对算法进行了验证。仿真结果表明，在阵元对称性较差的条件下，和差比相方法几乎失效，但和差比幅方法仍然保持了较好的性能。与和差比相方法相比，和差比幅方法无需进行区域划分，在原理上可适用于任意阵型，但受测向辅助波束的限制，其计算复杂度更高，可作为和差比相方法的有效补充。