大间距多轴一致性检测方法研究

张丽芳，王劲松，陈雅鑫，马泽同，江宝林

（长春理工大学 光电工程学院，长春 130022）

在现代武器序列中，多管武器发射系统以其发射速度快、火力密度大和覆盖范围广的特点，已成为现代战争中的主要威慑武器［1-2］。武器系统的多个发射轴之间的平行性以及发射轴与观瞄系统的瞄准轴间的一致性直接决定了武器系统的打击精度，因此多轴一致性问题是衡量多轴武器发射系统工作性能的一个重要参数。多轴一致性的传统检测方法主要有五棱镜法、激光光轴仪法、大口径平行光管法和投影靶板法等［3-5］。五棱镜法的测量装置分散，集成度低，测量误差较大，不适用于外场检测。激光光轴仪法的系统装配难度高，一般用于某些专用设备，通用性不强［4］。大口径平行光管法对光轴一致性测量精度高，但该方法受设备体积大的限制不适合携带，多用于实验室条件下的测量。投影靶板法是用激光器来把各个光轴投影到靶板上，通过对投影靶板上的光轴投影之间距离的测量，计算得到各轴之间的夹角，该方法结构简单，且光束的传输距离较远，可适用于在外场环境条件进行轴一致性的测试［3］，但其自动化程度低，测试效率差，精度低。本文提出一种基于全站仪的轴一致性检测方法，在不影响全系统装配状态的前提下，实现武器系统和观瞄系统轴一致性的检测，可对武器多发射轴间、武器系统发射轴与观瞄系统瞄准轴之间及观瞄系统激光发射轴和瞄准轴之间的一致性进行检测，对外场条件下武器打击准确性的快速评估具有现实意义。

1 测量原理

1.1 测量原理

该系统主要由全站仪、激光定位指示装置和靶板组成。其测量原理如图1所示，激光定位指示装置安装于被测发射筒内模拟武器系统的发射轴，调节全站仪使全站仪与观瞄系统中被测瞄准轴同轴，保证靶板与观瞄系统的瞄准轴垂直，将全站仪作为基准点，被测瞄准轴作为基准轴，将全站仪翻转180°测出全站仪与靶板之间的距离，沿全站仪的垂直轴将其旋转90°，通过光电瞄准（人眼对准）的方式测出全站仪与激光定位指示装置之间的距离及空间角，继续转动全站仪，使全站仪的测距激光与激光定位指示装置在靶板上的投影重合，测出全站仪与激光定位指示装置在靶板上的投影的距离及空间角，测量结果可以通过计算机计算或手动计算［6］，求出被测光轴之间的夹角。

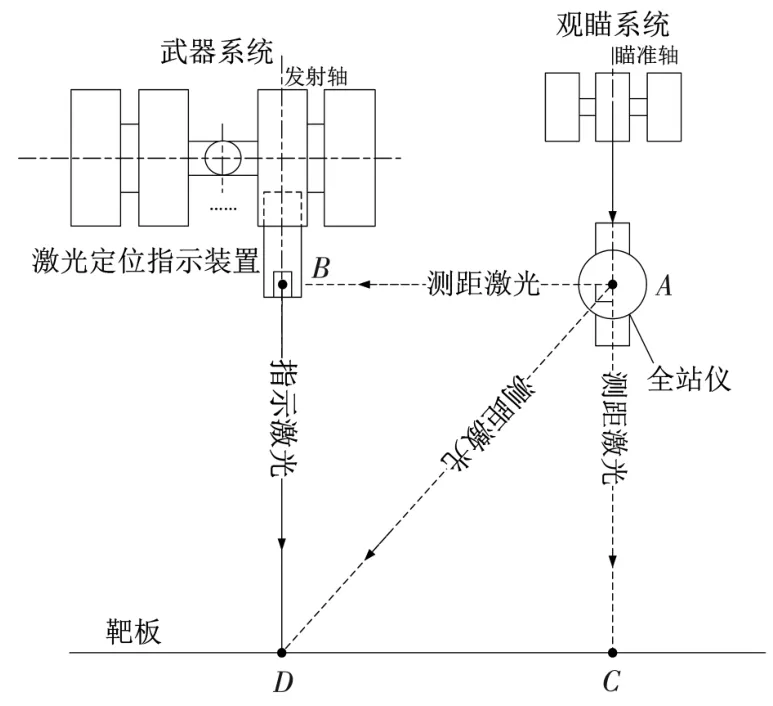
图1 发射轴与瞄准轴一致性检测原理图

1.2 一致性计算模型

武器系统的发射轴与观瞄系统的瞄准轴之间会存在空间夹角。以全站仪为基准点，记为A，激光定位指示装置中心轴与全站仪的测距激光光轴交点记为B，当全站仪与观瞄系统的瞄准轴同轴时，其测距激光在靶板上的投影为C，激光定位指示装置在靶板上的投影记为D。通过全站仪可测得全站仪与靶板、激光定位指示装置中心轴及投影点D之间的距离分别为d1、D1和d3，激光定位指示装置相对于全站仪的偏角为θa1、θp1，由测量原理可知θa1=90°，投影点D相对于全站仪的偏角为θa2、θp2。坐标定义和光轴偏角计算模型如图2所示［7］。

图2 一致性计算数学模型

通过上述分析，A、B之间的距离D1为：

其中，d0为激光定位指示装置直径；d2为全站仪与激光定位指示装置间的距离。

C、E之间的距离D2x为：

其中，θa2为投影点D相对于全站仪的水平角。

D、E之间的距离为：

其中，θp2为投影点D相对于全站仪的垂直角。

则C、D之间的距离D2为：

A、B分别向xOz、yOz平面投影为：

其中，θp1为激光定位指示装置相对于全站仪的垂直角。

最终可得瞄准轴与发射轴水平方向一致性的偏差角αh为：

瞄准轴与发射轴垂直方向一致性的偏差αv为：

2 误差分析

由公式（7）和公式（8）可知，影响多轴一致性检测精度的因素有：（1）距离d0、d1、d2、d3的测量误差；（2）垂直角度θp1、θp2的测量误差；（3）水平角度θa2的测量误差。采用微分法进行分析［8-9］。

（1）距离d0、d1、d2、d3的误差对检测精度的影响：

将公式（7）和公式（8）对距离取全微分：

距离d0、d2的测量误差是由全站仪的测量误差引起的，d1、d3的测量误差由全站仪的测量误差及靶板与全站仪的垂直度误差引起。按照在检测过程中靶板与全站仪的间距在20 m左右，全站仪与激光定位指示装置中心轴的间距为2～3 m，进行计算，会有，进行距离测量时，使用的是同一全站仪，其距离测量精度为2 mm+2 ppm，故有：

靶板与全站仪的垂直度采用全站仪对靶板进行自准直法调节，保证全站仪的出射激光能原路返回，计算可得其误差为2′，由于AC轴为基准轴，则靶板与全站仪的垂直度误差对d1的影响可认为不存在，故认为dd1=2.04mm，参考1.2节中的数学模型，经过分析与计算可知，靶板与全站仪的垂直度误差对d3的影响为2.9 mm，则：

当θp1≈θp2＝45°时，距离误差对检测精度的影响最大，带入数据计算可得：

（2）垂直角度θp1、θp2的误差对检测精度的影响：

将公式（7）和公式（8）对垂直角取全微分：

垂直角度θp1测量误差由全站仪的测量误差引起，垂直角度θp2由全站仪的测量误差及靶板与全站仪的垂直度误差引起，同理，在测量过程中使用的是同一全站仪，角度测量的精度为2″，则：

由上面的介绍可知靶板与全站仪的垂直度误差为2′，其对垂直角度θp2的影响经过计算可知为 8.09″，故：

当θp1≈θp2＝45°时，垂直角度的测量误差对检测精度的影响最大，此时d3≈1.42d1，将数据带入公式（15）和公式（16）中可得：

（3）水平角度θa2的误差对检测精度的影响：

将公式（7）和公式（8）对水平角取全微分：

水平角度θa2由全站仪的测量误差及靶板与全站仪的垂直度误差引起，经过计算，靶板与全站仪的垂直度误差对水平角度θa2的影响为5.2″，故：

参考1.2节中的数学模型，结合全站仪与激光定位指示装置、靶板之间的距离关系有θa2≈0°，从而会有：

（4）总误差对检测精度的影响：

水平方向的总误差为：

垂直方向的总误差为：

3 实验与数据分析

3.1 实验系统搭建

为了验证本文提出的检测方法对多轴一致性的实际检测效果，采用650 nm半导体准直激光器、电子经纬仪、激光测距仪、光学经纬仪、靶板等设备在光学平台上搭建原理样机，如图3所示［10］。

图3 多轴一致性检测方法的原理样机

选择其中一个激光器放置在长圆柱筒中模拟武器系统的炮筒及激光定位指示装置，将长圆柱筒固定在光学经纬仪上，通过光学经纬仪角度旋转模拟炮筒的转动，另外一个激光器光轴作为观瞄系统中的瞄准轴，激光测距仪固定于电子经纬仪上作为全站仪使用，可作为基准点，通过人眼对准的方式进行数据测量，计算出被测光轴之间的一致性偏角。

3.2 测量过程

该方法的操作步骤如下：

（1）进行电子经纬仪、激光测距仪与光学经纬仪的调平［9］。

（2）使用经纬仪与观瞄系统的瞄准轴对瞄，使经纬仪的瞄准望远镜对准观瞄系统的瞄准轴。

（3）将电子经纬仪沿俯仰轴翻转180°，角度置零，利用自准直法，调节靶板与测距仪垂直，通过测距仪测出其与靶板之间的距离d1。

（4）将电子经纬仪沿方位轴旋转90°，调节电子经纬仪的俯仰角测出激光定位指示装置相对于基准点的空间偏角为θα1、θp1，激光定位指示装置与基准点之间的距离d2，其中水平角θα1=90°。

（5）转动电子经纬仪使激光测距仪出射激光与激光定位指示装置出射激光在靶板上的投影重合，由此测出激光定位指示装置在靶板上的投影点相对于基准点的空间偏角θα2、θp2以及投影点与基准点之间的距离d3。

（6）根据1.2节中推导出的计算轴一致性偏差角的公式（7）和公式（8）计算发射轴与瞄准轴的一致性偏差，从而实现多轴一致性的检测［11］。

3.3 数据分析

按照本文提出的多轴一致性检测方法的操作步骤，可以得到初始位置时的测量数据为A（0°，90°，0），B（90°，92°58′55″，580 mm），C（0°，90°，4 793 mm），D（6°40′26″，，92°50′48″，4 819 mm），光学经纬仪的读数为（93°28′30″，89°07′50″），根据公式（7）和公式（8）可以算出此时两光轴之间的水平偏角αh0为 15.67″，垂直偏角αv0为 9.52″。首先保证光学经纬仪俯仰方向不动，将光学经纬仪沿方位轴进行微动，记录光学经纬仪水平方向的角度偏转为∆θh，重新通过电子经纬仪和激光测距仪测出经过偏转后C点和D点的数据，根据公式（7）计算出该位置时发射轴与瞄准轴的水平偏角，与初始位置的水平偏角做差值计算，将光学经纬仪的偏转角与该差值作比较，得到实际偏角与测量偏角的误差值，重复上述步骤进行10次［12-13］，测量数据和计算结果如表1所示。

重新确定一个初始位置为A（0°，90°，0），B（90°，92°52′55″，578 mm），C（0°，90°，4 793 mm），D（6°58′26″，92°50′35″，4 820 mm），光学经纬仪的读数为（93°28′30″，89°07′50″），此时两光轴之间的水平偏角αh1为 15.64″，垂直偏角αv1为 9.5″。然后保证光学经纬仪方位方向不动，将光学经纬仪沿俯仰轴进行微动，记录光学经纬仪垂直方向的角度偏转为∆θv，重新通过电子经纬仪和激光测距仪测出经过偏转后C点和D点的数据，根据公式（8）计算出该位置时发射轴与瞄准轴的垂直偏角，与初始位置的垂直偏角做差值计算，将光学经纬仪的偏转角与该差值作比较，得到实际偏角与测量偏角的误差值，重复上述步骤进行10次，测量数据和计算结果如表2所示。

表1 水平方向测量数据

表2 垂直方向测量数据

由表1和表2中实验数据可知，使用本文提出的方法进行测试时，水平方向一致性的最大偏角为 19.08″，平均值为 15.66″，标准差为 2.52，与本文方法检测的水平方向偏差23″相比，在误差范围内一致。垂直方向一致性的最大偏差角为 15.09″，平均值为 13.57″，标准差为 1.47，与前述误差分析的垂直方向偏差17″一致。由于实验室空间的影响，实验室检测距离为实际检测距离的1/4倍，而检测距离越远，产生的误差就会越小［14］，即实际检测误差完全满足本文检测方法的误差范围。从而验证了本文方法的正确性。

4 结论

本文提出了一种基于全站仪的多轴一致性检测方法，首先进行了检测方法的叙述与建模，接着利用全微分法将会影响到检测精度的因素进行了分析与计算，最后对提出的方法进行了验证性实验，并对实验数据进行相应的分析。实验结果表明：该方法适用于测量大间距轴间的空间夹角，测量精度可达到20″以内。该检测方法采用了模块化设计、制造，该方法中所需设备体积小，便于安装和控制，较好地解决了传统人工检测的效率问题，改进了检测方法，提高了检测的精度与效率。