焦斑投影法检测发射轴和瞄准轴一致性

陈雅鑫，王劲松，马泽同，张丽芳，江宝林

（长春理工大学 光电工程学院，长春 130022）

多管武器以其高发射速度和大火力密度成为现代战争中的有力威慑，为了提高其打击精度，对多管武器性能参数的精度检测要求也越来越高，尤其是多管武器发射轴间、发射轴和瞄准轴间、激光发射（测距）轴和瞄准轴间的一致性是直接影响武器成功命中目标概率的重要指标之一［1-2］。除此之外，复合光电瞄具系统和双目望远镜在军事上的应用也十分广泛，其轴间一致性也是决定其性能的关键指标。显而易见，多管武器和复合光电瞄具系统轴间一致性的检测意义重大。目前传统的室内条件下轴间一致性检测方法有平行光管法、离轴抛物镜法、五棱镜法和靶标法。在外场条件下的主要测试方法有投影靶标法、像纸法和CCD法［3-7］。传统方法有很多问题存在，这种室内检测方法虽然精度较高，但使用场合有所限制，不适合外场检测，适合外场检测的方法对场地大小有一定要求，布站时间长，工作强度大，受环境影响大，测量效率和精度较低。为适应室内和室外通用，本文提出焦斑投影法检测发射轴与瞄准轴间的一致性，采用瞄准目标模拟光路（瞄准轴）和激光接收（发射轴）光路共光路耦合结构，通过CCD相机对激光光斑图像进行数字化测量，具有测量精度高，适用性强的特点。

1 测量装置及检测原理

1.1 测量装置

如图1所示，该测量装置主要由发射管激光定位指示装置、分光棱镜SP1、分光棱镜SP2、物镜L、反射棱镜RP、投影屏、靶标、毛玻璃、辐射源、电源、CCD相机、图像采集卡和计算机组成。其中，多发射管武器系统和观瞄系统为被测件，分光棱镜SP1和反射棱镜RP之间的距离可调整，靶标根据观瞄系统的瞄准装置波段可分为可见光田字格分划和红外田字格分划。

根据焦斑投影法散斑产生机理，被测激光经准直物镜后会在物镜焦平面处形成一个圆形光斑，即要求投影屏位于物镜L的焦平面处，和靶标处于等效位置，同时投影屏位于成像物镜的物平面，CCD相机位于成像物镜的像平面。图1中实线光路为两轴一致时的理想光路，虚线光路为两轴不一致时的光路，产生的夹角为θ，投射在投影屏上的光斑偏离理想光轴的距离为Δx，光斑像到CCD相机的光敏面中心的距离为Δx′，物镜L焦距为f′，根据焦斑投影法和几何光学原理，有：

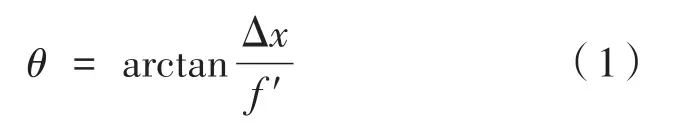
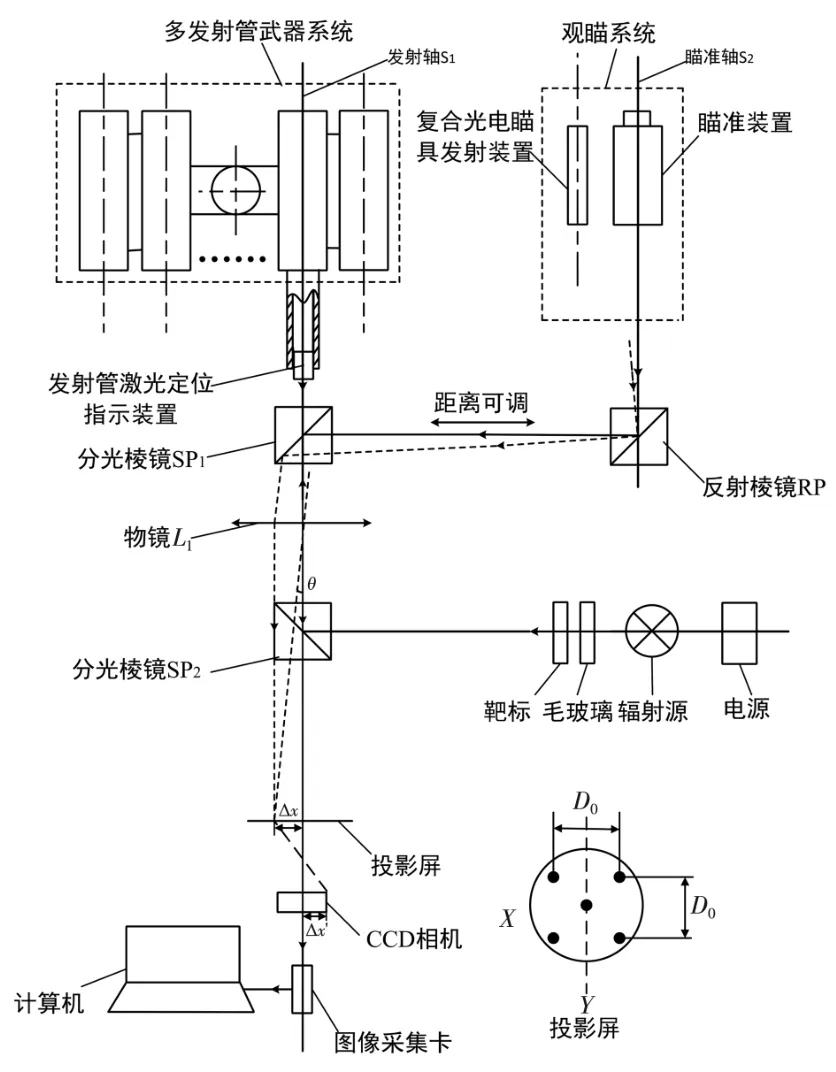
图1 测量系统工作原理图

已知成像物镜的放大倍率为β，根据投影屏上的光斑和CCD相机中光斑的物像关系，则公式（1）可以换算为：

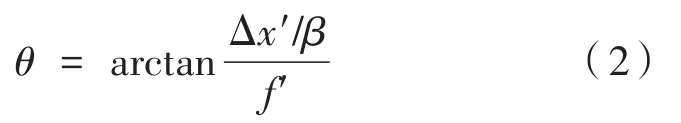
通过图像处理技术解算得到光斑质心与投影屏中心之间像素数N1、N2、N和像素的大小d，公式（2）又进一步换算为：

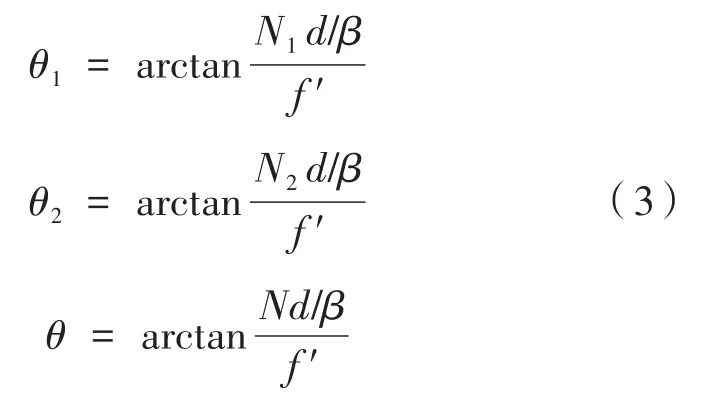
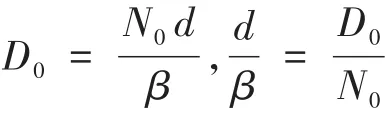
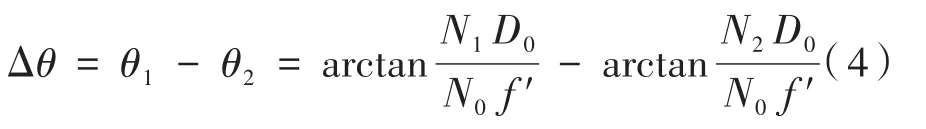
则测量发射轴和瞄准轴一致性和测量两瞄准轴一致性时，N1或N2等于零，则：

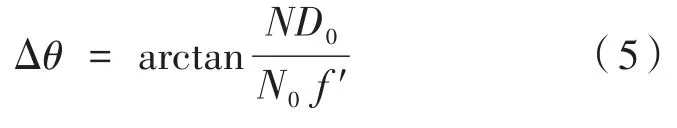
1.2 发射轴和瞄准轴间一致性检测

首先通过观瞄系统的瞄准装置对准检测装置的靶标中心，然后使模拟发射轴的发射管激光定位指示装置发射激光，经过分光棱镜SP2后使激光光斑成像在投影屏上，通过图像处理求得激光光斑的质心与投影屏中心的像素数，即光轴偏移量，最终根据公式（5）求得两轴之间的夹角。

检测两发射轴间一致性和检测两瞄准轴间一致性的原理与此相同，其中的光轴偏移量分别为两个激光光斑质心之间的像素数和双目望远镜的两个镜筒十字线中心之间的像素数。

1.3 理论误差分析

（1）测量两发射轴一致性时，对公式（4）进行全微分计算，有：

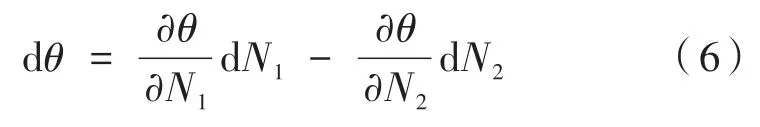
影响两发射轴一致性检测精度的因素主要有像素数N1和N2的图像处理误差，而D0引起的标定误差和物镜焦距的安装误差属于系统误差，多次测量相消。

像素数N1和N2的误差对检测精度的影响，对N1和N2取全微分有：

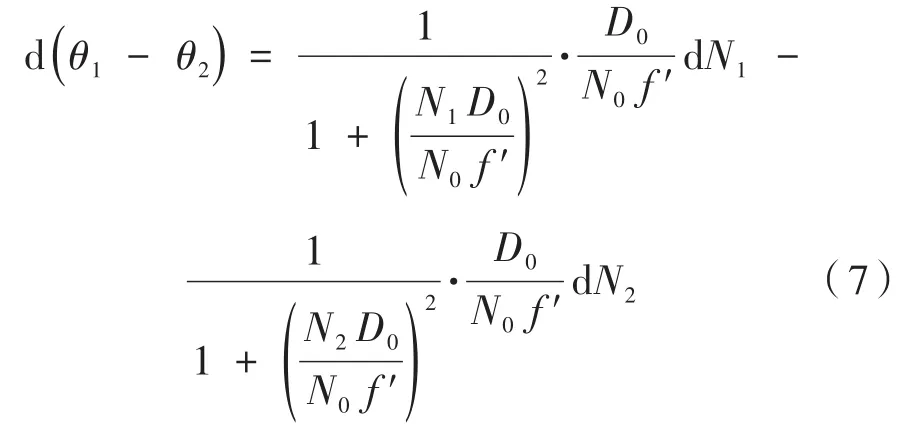
影响像素数N1和N2的误差主要由图像处理引起，包括质心的定位误差和质心之间像素数的解算误差，按照8位像素细分计算有：

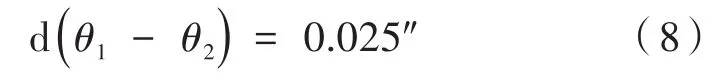
发射管激光定位指示装置与多发射管武器系统之间是间隙配合，定位长度为200 mm，根据现有精密机械定位工艺水平，炮管轴线激光指示装置的定位精度可以达到7″。

检测两发射轴一致性时总误差对检测精度的影响为：

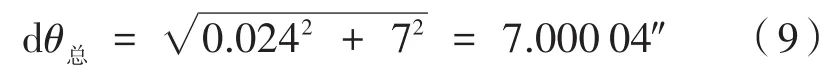
（2）测量发射轴和瞄准轴一致性和两瞄准轴一致性时，对公式（5）进行全微分计算，有：

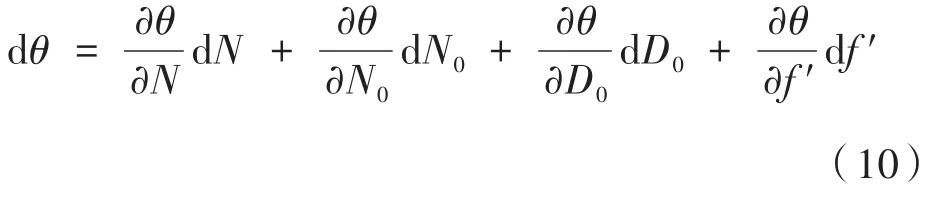
由公式（9）可以看出，影响两轴一致性检测精度的因素主要有：（a）光斑质心与投影屏中心之间的像素数N的图像处理误差；（b）两标定点间距离D0的标定误差；（c）物镜焦距的安装误差。其中光斑质心与投影屏中心之间的像素数N带来的影响与上述分析相同，经过计算有：

两标定点间距离D0对检测精度的影响：

对D0取全微分有：

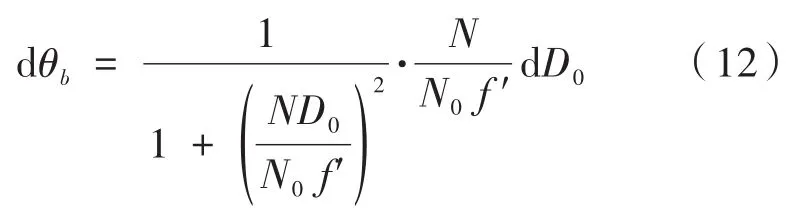
影响D0的误差主要由投影屏标定点距离标定引起的，经计算可得：

（3）物镜焦距f′对检测精度的影响：

对f′取全微分有：

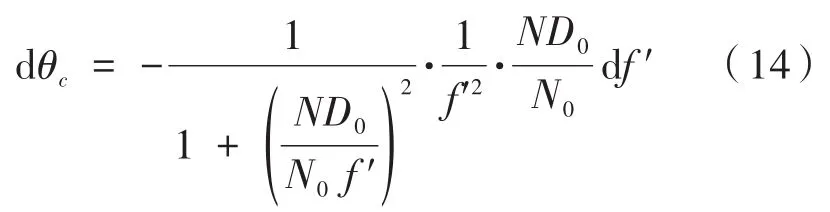
影响f′的误差主要是物镜的安装误差引起的［8-9］，经过计算可得：

由于D0和f′引起的误差和分光棱镜SP1和反射棱镜RP对应的加工误差，都属于系统误差，不参与总误差对检测精度影响的计算。

除以上分析的误差外还有人眼瞄准误差，由于瞄准镜物镜放大率为Γd=3，即瞄准误差为3.3″［10］，所以检测发射轴和瞄准轴一致性和检测两瞄准轴一致性时的总误差大小为：

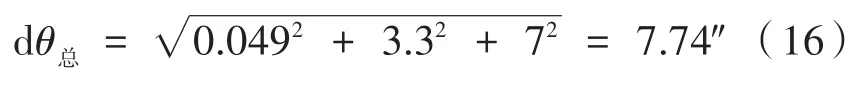
2 检测实验及数据分析

2.1 测量实验平台的搭建

根据测量原理在光学平台上搭建测量实验平台，测量发射轴和瞄准轴间一致性的实验平台如图2所示。若检测发射轴间一致性，只需将瞄准镜换成代表发射管的钢管即可。其中发射管定位指示装置、物镜L和投影屏组成激光光斑焦斑投影系统，其作用是测量原理的体现，是整个检测系统的核心，实验采用钢管模拟武器发射管，用发射管激光定位指示装置模拟发射轴，用带有五个标定点的投影屏接收激光光斑，投影屏的材质是半反半透的，避免激光能量太强损坏CCD。本实验系统的测量范围为±30 mil，物镜口径为60 mm，焦距为880 mm，因此可以确定投影屏大小89 mm，设置两标定点之间的距离为投影屏大小的四分之三最为合适，即两标定点之间的距离为67 mm。物镜、靶标和辐射源构成无限远目标模拟系统，作用是为检测发射轴和瞄准轴间一致性提供无限远目标，快速调整系统轴间一致性。CCD相机、图像采集卡和计算机构成视觉图像采集系统，实现投影屏上光斑信息及靶标信息的采集及处理的功能，得到光斑的位置信息并最终解算轴间一致性。相机采用的是海康威视DS-2CD5032FWD-A，镜头参数为f=8 mm，通过网线直接与计算机相连，实时采集激光光斑图像。选用LED光源作为测量系统的辐射源，有效光谱范围可以覆盖可见光及近红外波段。

图2 发射轴和瞄准轴一致性检测实验平台

实验中采用经纬仪提供标准值，以便和测量值进行对比。将模拟多管武器发射管的钢管安装在经纬仪上，可以使经纬仪同步转动，调整检测装置轴一致性后，记录经纬仪的角度值，该值作为参考基准。

2.2 实验数据处理及分析

测量两个发射轴间一致性时，将计算机获取到的激光光斑图像采用MATLAB进行图像处理，采用灰度线性变换法进行图像增强，通过最大类间方差方法找到一个合适阈值进行图像二值化，边缘检测采取了LOG算子和形态学处理相结合的方法，具有亚像素的定位精度，采用基于圆拟合的激光光斑中心检测算法求得光斑质心坐标［11-15］，通过距离公式求得两光斑之间的像素数，最终由公式（4）得到两轴之间的夹角，图像处理流程如图3所示。

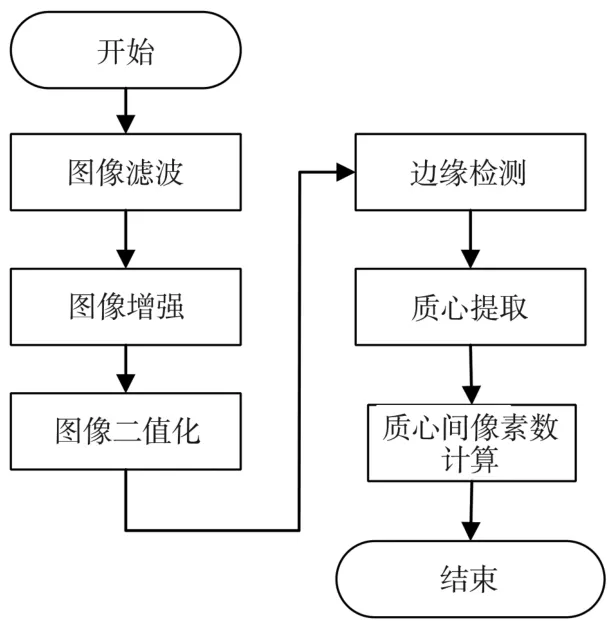
图3 图像处理流程图

用经纬仪将检测范围 ±30 mil平均分为10个角度测量，转过3 mil角度时两个激光光斑的相对位置如图4所示。根据兵器测试领域业界习惯，采用两个分量表达轴一致性检测夹角的大小，更加直观，并且综合被测夹角水平分量改变但垂直分量不改变、水平分量不改变但垂直分量改变和水平分量及垂直分量都改变三种情况的实验对比，得出水平分量改变但垂直分量不改变时，实验误差最小。实验数据如表1所示。

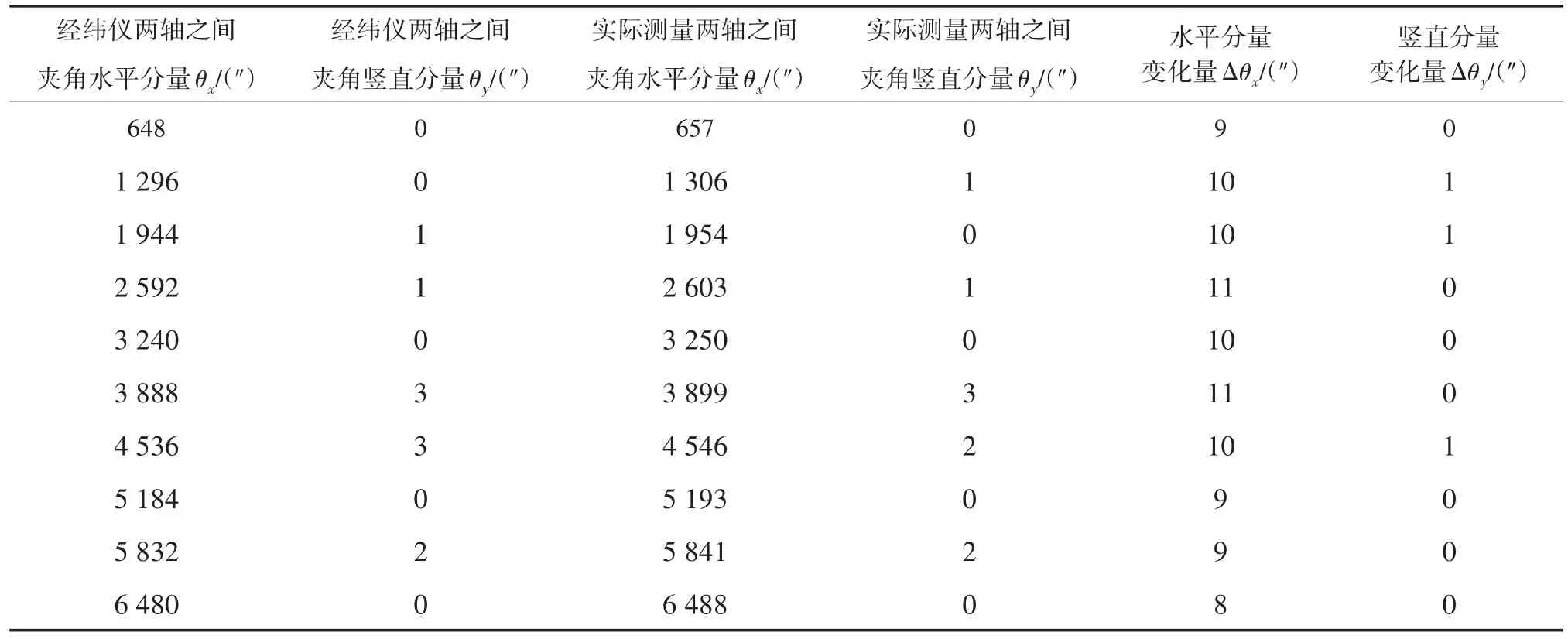
表1 发射轴间一致性检测实验数据

图4 发射轴间一致性检测激光光斑图像

由三次实验获得的数据绘制成θx-Δθx的关系曲线图（图5）可以看出，随着经纬仪转动角度的变化，可以得到该测量装置的测量范围为±30 mil，且水平分量误差在10″左右变化，将系统误差剔除后计算得出，发射轴间一致性检测的误差平均值为9.7″，标准差为2.76″，在此装置的测量范围内，误差分布均匀，能够满足大多数系统的测量需求。θy的测量和分析与θx的相同。

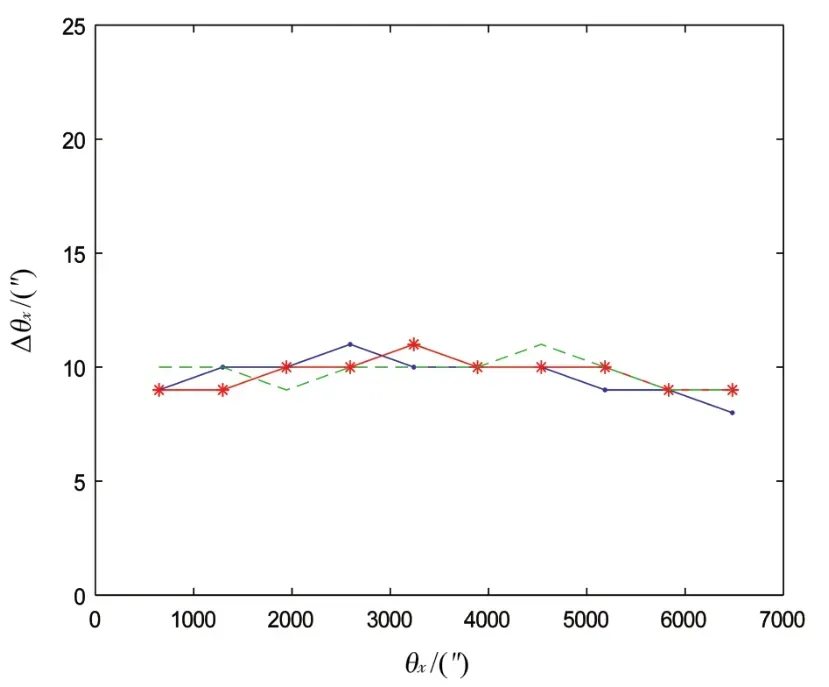
图5 发射轴间一致性θx-Δθx的关系曲线图

测量发射轴和瞄准轴一致性时，将瞄准装置、靶标和投影屏的轴线调一致后，通过CCD相机采集图像到计算机中，进行图像处理，得到激光光斑质心与投影屏中心的距离，再采用公式（4）求得两轴之间的夹角。瞄准装置中十字线中心与靶标田字格中心重合的图像如图6所示，实验数据如表2所示。

表2 发射轴和瞄准轴一致性检测实验数据

图6 瞄准镜十字线中心与靶标中心重合图像

由三次实验获得的数据绘制成的θx-Δθx关系曲线图（图7）可以看出，在系统测量范围内，误差变化均匀，将系统误差剔除后计算得出，水平分量误差平均值为9.8″，标准差为2.76″，但由于引入了瞄准装置十字线对准靶标田字格中心时的瞄准误差，计算结果可能存在一定偏差。θy的测量和分析与θx的相同。

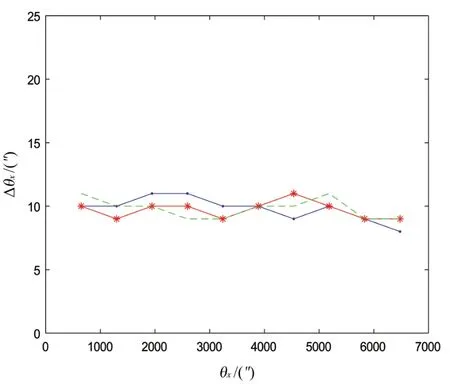
图7 发射轴和瞄准轴间一致性θx-Δθx的关系曲线图

测量两瞄准轴一致性时，已知靶标的田字格设计为每5 mil一个格值，所以根据这个参数就可以计算出两个瞄准轴之间的距离，最后也可以根据公式（4）得出两瞄准轴之间的夹角。

3 结论

通过焦斑投影法数学模型的建立，实现了大间距发射轴和瞄准轴之间夹角的测量，与传统方法相比，焦斑投影法的优点在于测量精度高且适用性强。采用微分法对两轴之间角度进行了误差分析，能够实现轴一致性误差平均值控制在9.8″以内，在理论误差分析范围内，满足大多数系统轴一致性检测需求。经模拟实验搭建和MATLAB软件仿真得到此装置在±30 mil的测量范围内，误差在10″上下均匀变化。在后续的研究工作中，需要对图像处理算法进行改进，使激光光斑中心定位更加准确。