车载跟瞄转台的扰动补偿控制技术研究
2022-08-26吴忠明张立中白杨杨孟立新张乐仪
吴忠明 ,张立中 ,白杨杨 ,孟立新 ,张乐仪
(1.长春理工大学 机电工程学院,长春 130022;2.长春理工大学 空地激光通信国防重点实验室,长春 130022)
车载光电跟瞄转台应用于空间激光通信,主要进行目标的捕获、跟踪和瞄准,完成载体间的通信[1-2]。在复杂的车载环境下,转台受到车辆姿态变化、路面振动冲击、外界风载扰动、自身不平衡力矩以及摩擦力矩等扰动力矩的影响[3]。为了保证车载跟瞄转台可以对运动目标进行高精度稳定跟踪,就要求控制系统具有很强的扰动抑制能力。传统的线性PID控制已难以满足高精度稳定跟踪的要求[4],因此,可以从控制算法的角度,采用一些扰动补偿控制方法。
目前,在光电跟踪系统中对扰动补偿方法应用的越来越多,文献[5]将自抗扰控制[6]用于望远镜光电跟踪系统的速度环,以补偿和抑制跟踪系统存在的摩擦等非线性问题,改善了系统的速度控制性能;文献[7]将前馈控制应用于舰载平台,将扰动量的一阶导数作为速度前馈,进行补偿,系统的跟踪精度提高了一个数量级;文献[8]将干扰观测器应用于三轴转台,用以补偿外部扰动力矩的影响,平台速度误差得到提高。
本文在传统的PID控制基础上,将速率陀螺测得载体姿态变化的角速度加入到速度环输入端,进行可测扰动的前馈补偿,再将自抗扰控制中的扩张状态观测器加入到位置环控制器,通过PI+ESO控制实现对转台位置和外部未知扰动的实时观测和补偿,提高系统的抗干扰特性,进而提高系统的跟踪精度。通过在MATLAB中对跟瞄转台方位轴系统(包含驱动器、电机以及机械负载)进行仿真测试补偿方法的效果,最后在车载跟瞄转台控制系统中进行跟踪性能测试,验证算法的有效性。
1 伺服系统组成及原理
搭建方位轴的开环控制系统:直流力矩电机、SA57驱动器、23位增量式光栅编码器、CCD可见光相机、单轴光纤速率陀螺。进行转台方位轴开环频率测试,输入频率连续变化的正弦扫频信号,通过ARM+FPGA处理器实时读取方位电机编码器位置信息,上位机连接控制器采集数据,并将数据保存后进行处理,通过相关分析法[9]得到采样数据的幅频和相频曲线,建立直流力矩电机模型,采用自适应差分进化算法[10]辨识控制系统的传递函数模型,最后根据传递函数模型进行控制器设计,完成仿真分析和实验测试,其不考虑高频段辨识的转台方位轴传递函数为:

其伺服系统组成如图1所示。
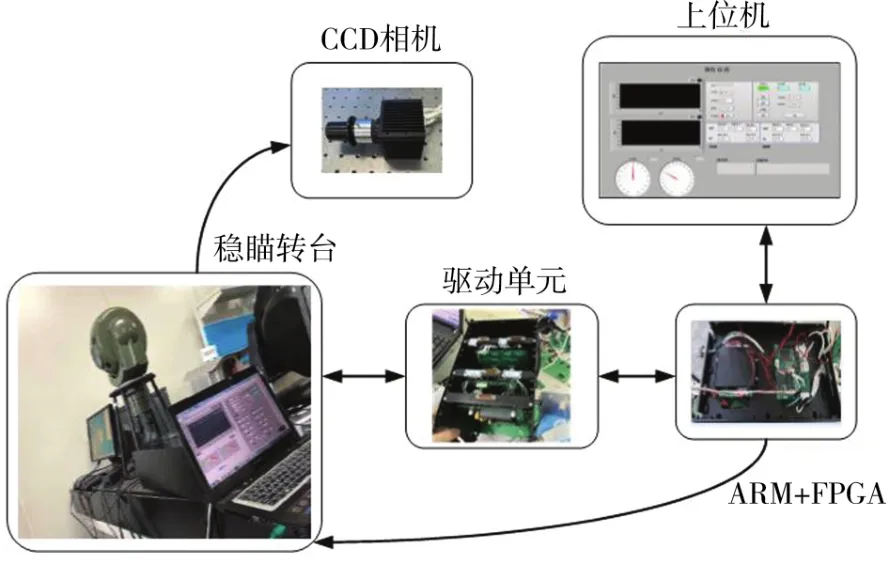
图1 伺服系统组成
2 陀螺速度前馈
前馈控制的原理就是使系统多一个前馈通道,被测得的已知扰动可以通过前馈控制器改变控制量。利用扰动附加的控制量与扰动量影响的叠加消除或减少干扰的影响。
根据前馈控制的特点,将车载跟瞄转台方位轴和俯仰轴的速率陀螺测得的车体振动速度作为干扰源,前馈到速度环输入端,陀螺速度所对应的车体振动、摇摆作为位置环输入端的输入量,这样通过前馈控制补偿可以达到隔离车体振动的作用。图2为前馈控制原理框图,图3为传递函数简化框图。
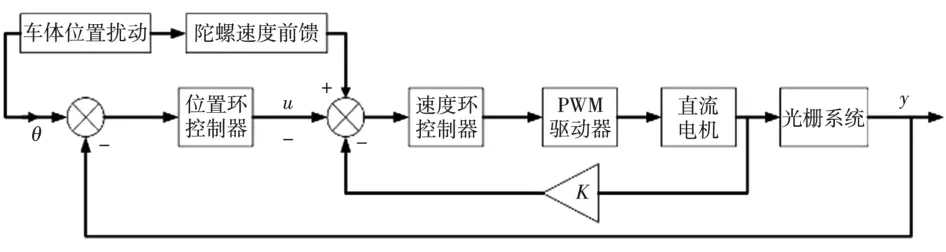
图2 前馈控制原理框图

图3 传递函数简化框图
图3中,U(s)是位置变化量输入,E(s)是误差信息,C(s)是位置环控制器,G(s)是速度闭环传递函数。可得系统的传递函数和误差控制函数为:
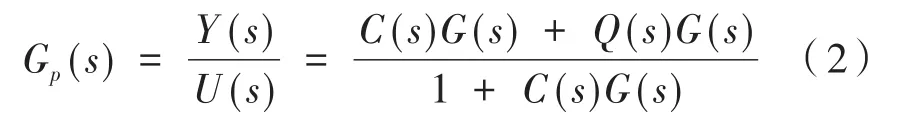
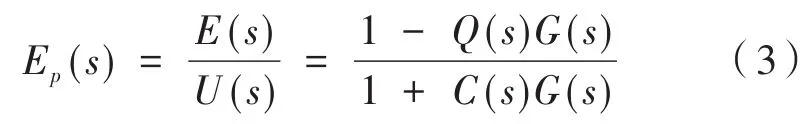
由此可以看出,只要让式的分子为零,则可以控制误差为零,得:
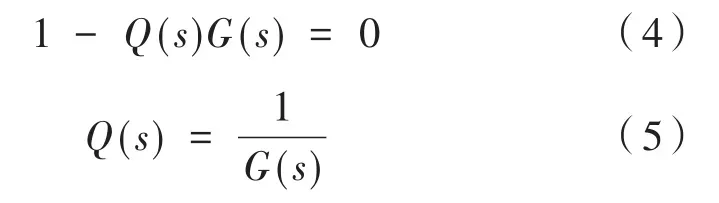
G(s)为速度闭环传递函数,可以简化为一阶小惯性环节为:
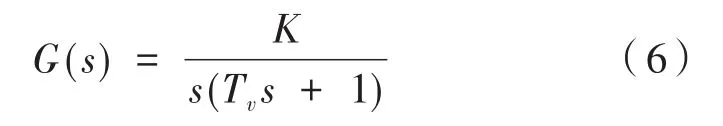
其中,K是闭环增益;Tv是速度闭环经过等效后的时间常数,可得:
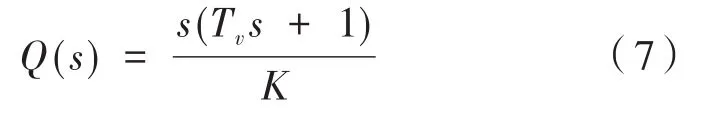
可以看出Q(s)为输入信号一阶、二阶或更高阶的导数所构成。由此可将车体振动摇摆信息作为输入,速率陀螺测得速度量作为速度前馈输入到速度环控制器,达到隔离车体振动带来的已知扰动。
采用单轴速率陀螺测量在车体实际振动条件下陀螺的速度输出,并用上位机采集一定时间数据,根据采集的数据在MATLAB中进行有无前馈控制的仿真,分为以下两种情况:
(1)将采集到的陀螺速度值进行积分处理,作为位置环的位置输入,然后将速度值前馈到速度环输入端,得到位置跟踪误差;
(2)将采集到的陀螺速度值进行积分处理,只作为位置环的位置输入,不进行前馈控制的补偿,得到位置跟踪误差。
图4、图5分别为有无陀螺速度前馈的跟踪误差,对比两次仿真中的跟踪精度。采用前馈控制,误差最大值为0.013 77°,均方差0.003 439°(1σ),不采用前馈控制误差最大值0.048 95°,均方差0.015 81°(1σ)。可得速度前馈有一定的隔离车体振动的效果。
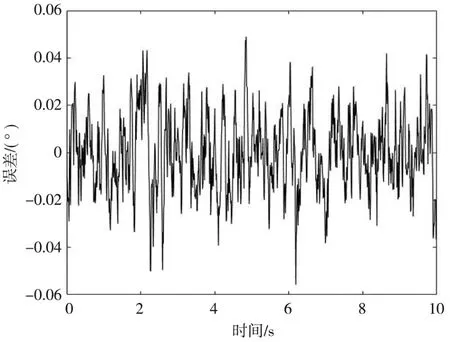
图4 无速度前馈跟踪误差
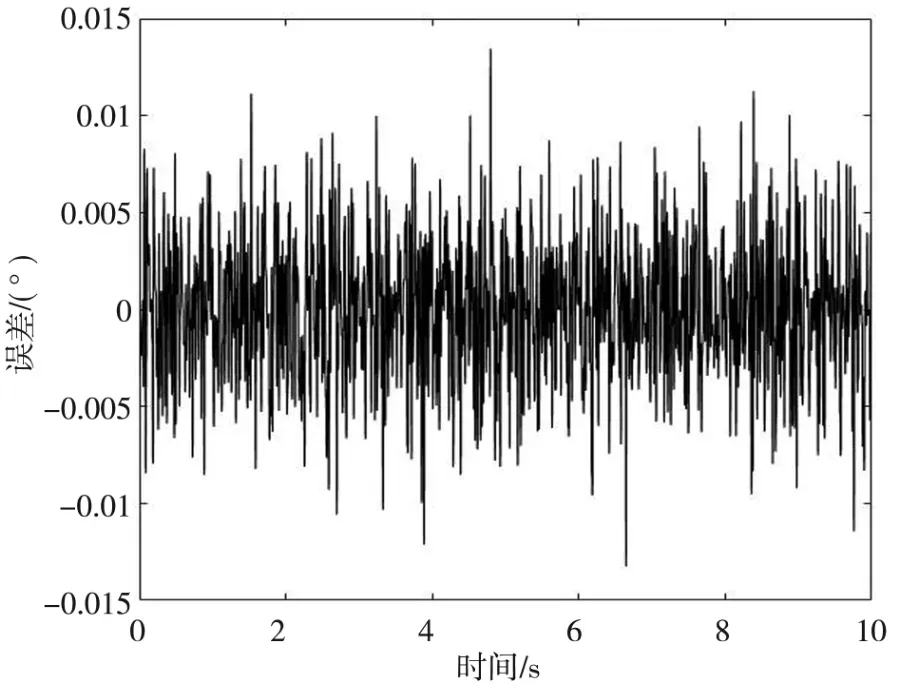
图5 有速度前馈跟踪误差
3 设计扩张状态观测器
3.1 扩张状态观测器
扩张状态观测器是自抗扰控制技术[5]的核心部分,它将控制系统的内部扰动以及外部扰动当成一个未知的状态变量,进而得到一个新的状态观测器,由于扩张了一个新的状态变量,所以称为扩张状态观测器。扩张状态观测器不需要对扰动进行测量,也不需要系统本身有关扰动的任何先验知识,只需要根据系统输入信号以及输出信号数据,就能够实时估计系统状态以及扩张的扰动。因此,扩张状态观测器得到了广泛使用。扩张状态观测器(ESO)可以对系统的未知扰动进行预测和跟踪,通过多级变换,可以将系统转化为积分结构应用于传统PI控制。
3.2 基于位置环的ESO
ESO的核心思想将跟瞄转台经过光栅编码器取得的位置信息中的未知扰动经过扩张状态观测器,可以实现对跟瞄转台的位置环、速度内环和不确定变量进行预测和补偿,进而通过调节参数,提高跟踪精度。其中位置环的ESO框图如图6所示。
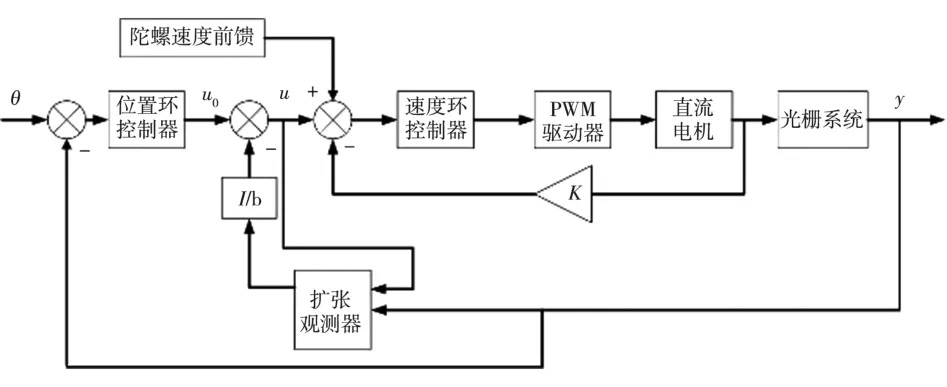
图6 位置环ESO框图
速度环控制器设计的主要目的是保证系统的带宽和相位裕度满足要求,采用超前滞后校正设计速度环控制器,在低频段,速度闭环传递函数可近似等效为一阶惯性环节,考虑到编码器的传递函数可等效为积分环节,位置环被控对象可以表示为:
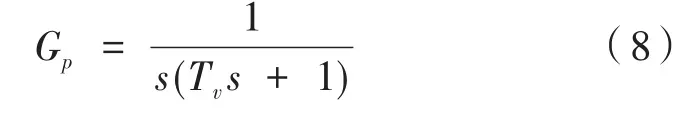
将其转换为状态方程为:
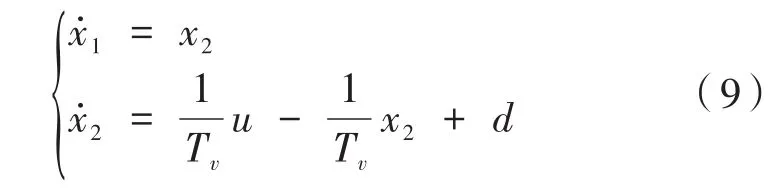
其中,x1为位置测得量;1为位置求导,即速度值;x2为速度测得量;u为扩张状态观测器控制量;d为转台未知扰动。利用光栅位置量设计扩张观测器,以实现对状态观测器的准确估计。将作为被扩张的转态变量x3,即,其导数为m(t),令,则系统可扩展为一个新系统:
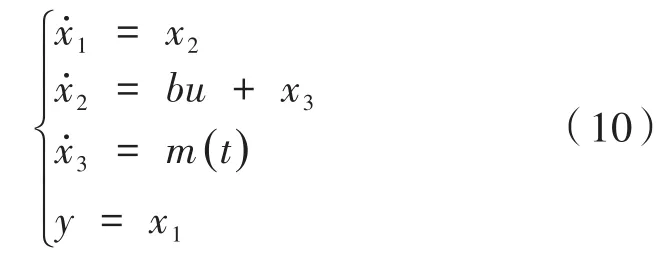
新系统中,扩张状态观测器通过转台输出响应和设计的控制量,可以对系统状态变量进行估计,进而设计三阶扩张状态观测器,对速度、位置和未知扰动进行观测补偿,如下:
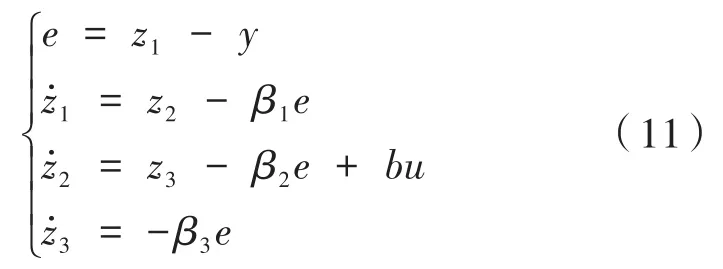
其中,z1、z2、z3为位置、速度和不确定因素的估计值;y为被控对象输出,即编码器采集位置量;β1、β2、β3为观测器的增益。令e1=z1-y=z1-x1,e2=z2-x2,e3=z3-x3,可得误差方程为:
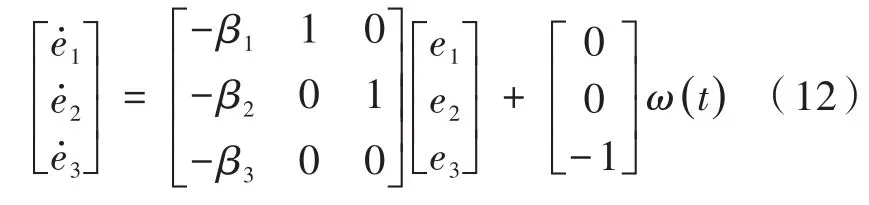
可以看出扩张状态观测器是一个有着两项输入三项输出的系统,为了可以很好地抑制干扰,引入观测器带宽ω0,而且β1、β2、β3满足如下关系,特征方程表示为:
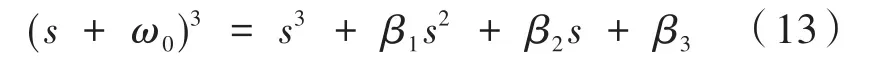
其中,ω0为设计观测器控制带宽。ω0的选取值越大,对状态变量的估计越准确,一般情况下ESO适应范围较宽,参数较容易整定,但系统噪声增大,所以应根据实际进行选择。根据带宽需要就可以确定线性 ESO 的参数,将位置环控制器输出设置为u0,将扩张状态变量估计值z3作为一个反馈值,进而可以对系统控制量进行修正,可以设计带动态补偿的作用式,如下:
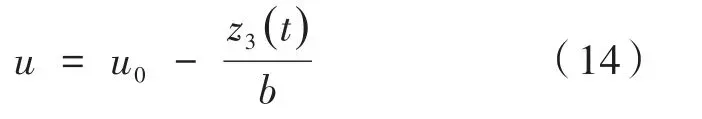
其中,b可以看作是控制量的放大倍数。则校正后系统可写为:
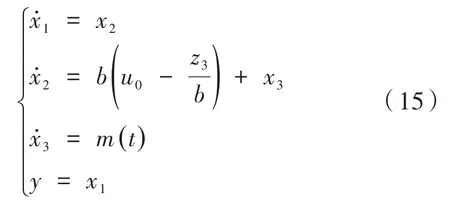
可见校正后系统是一个连续积分串联型系统,可以根据z3的控制律对系统进行动态补偿,通过上面两式可以得到:
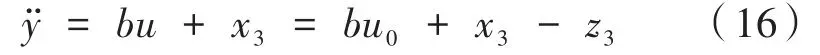
式中,x3近似等于z3。ESO的几个参数需要合理选择,进而可以得出z3的观测值,从而对位置环控制器的输出进行修正,系统可以转换为一个积分式:
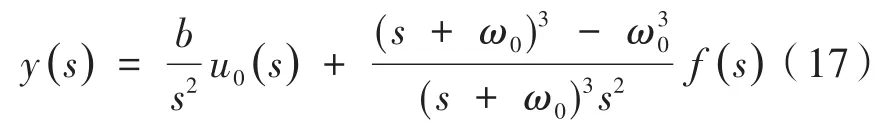
由于微分环节对系统噪声较敏感,因此根据上式设计位置环的PI控制器为:
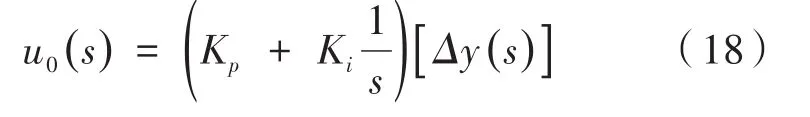
通过选择PI控制器的KP,Ki,根据转台输出量,并将其作为反馈量,不断进行输出量的反馈,在扩张状态观测器下对系统的未知扰动进行补偿,用补偿后的控制量重新设计传递函数,从而位置环PI控制器的传递函数可以写为:
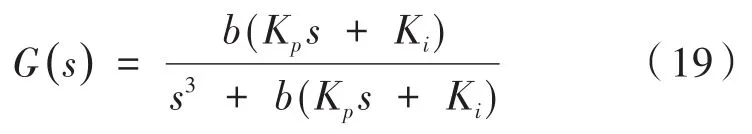
通过上述设计的控制器,以公式(1)的传递函数模型为例在MATLAB的Simulink中建立ESO的仿真模型,如图7所示。经过速度环的闭环控制后,进行带有扩张状态观测器的位置环控制。
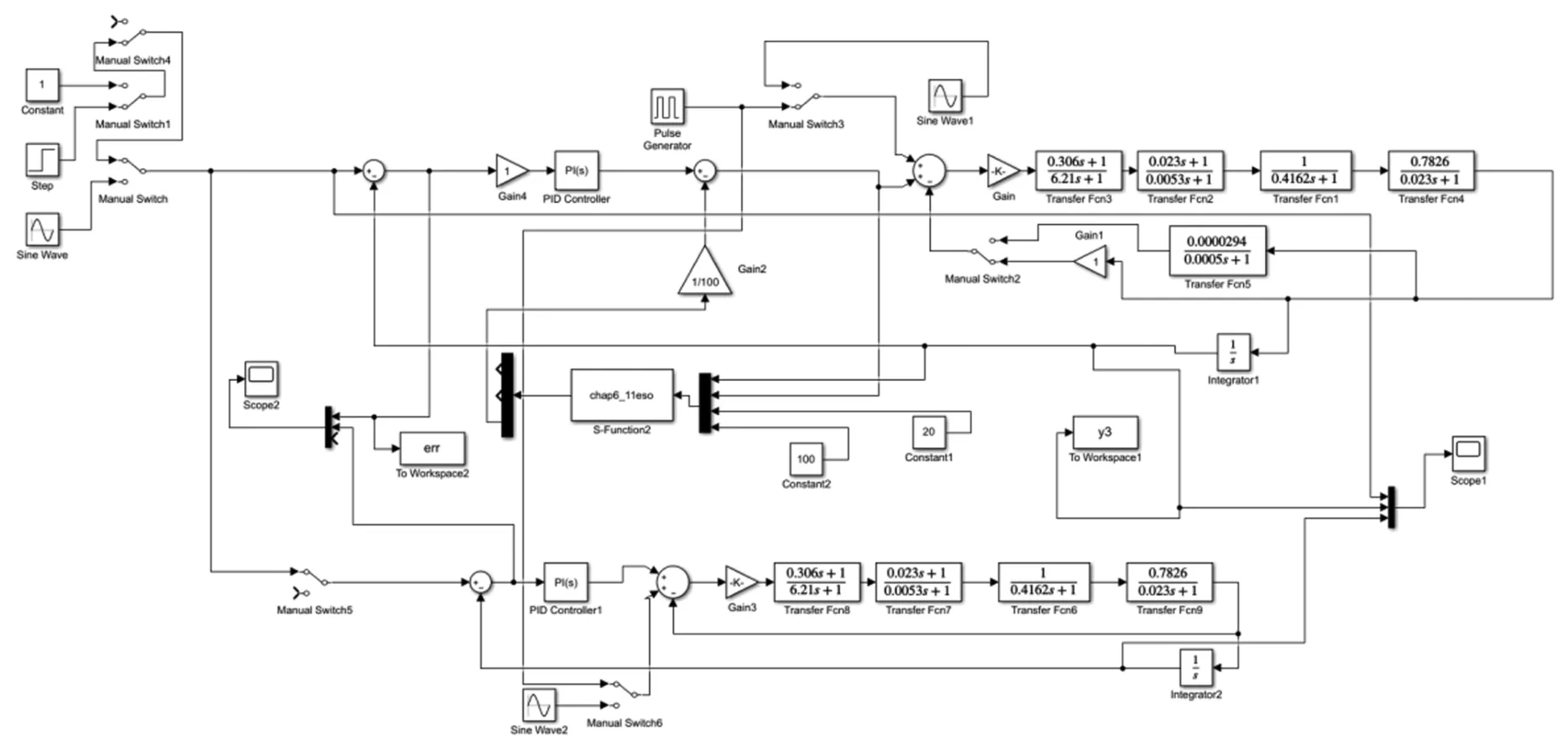
图7 ESO仿真框图
在PI控制器参数Kp、Ki,系统增益b一定的情况下,给定跟瞄转台最大角速度10°/s,角加速度 10 °/s2的等效正弦θ=10sin(t)°,得到ω0=5、10、20、40、70带宽下的正弦跟踪误差曲线和局部放大曲线如图8、图9所示。
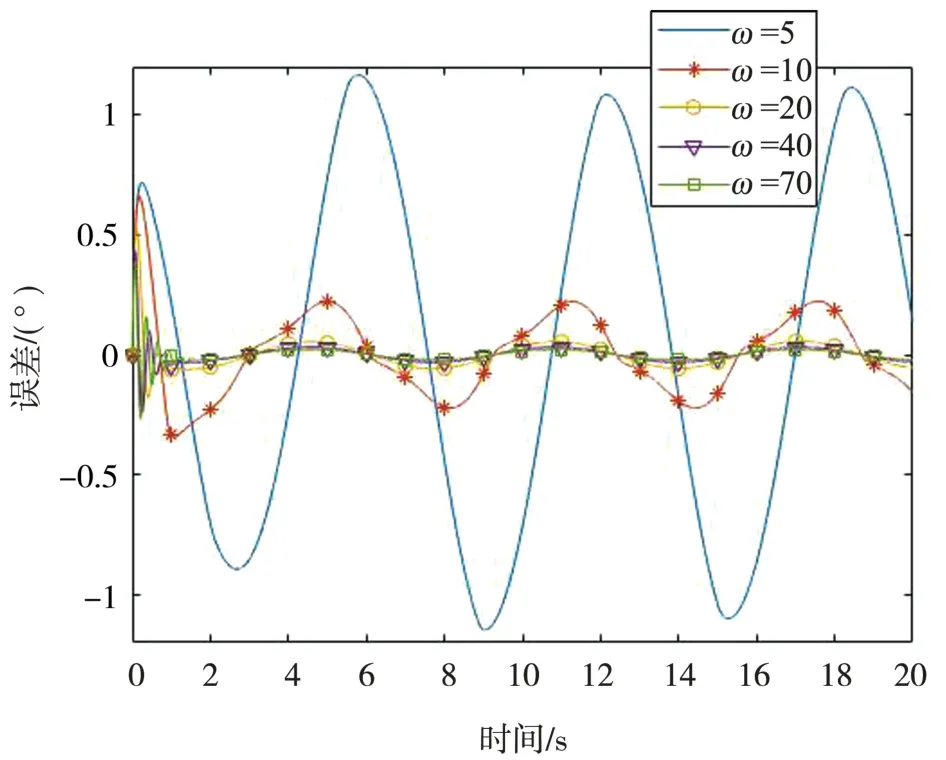
图8 正弦跟踪误差
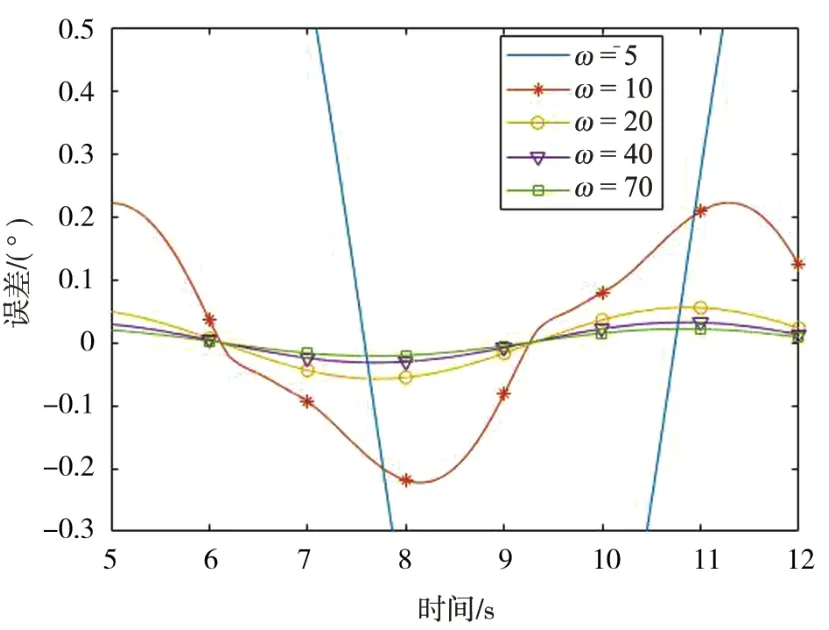
图9 跟踪误差局部放大图
可以看出随着观测器带宽ω0的增大,正弦跟踪稳定后最大误差由1.1°减少到了0.002 114°,跟踪精度逐渐提高,由扩张状态观测器原理可知,随着ω0的增大,估计值z3对系统不确定扰动的估计值越准确,进而提高系统跟踪精度。但是也可以看出跟踪初期调节时间逐渐增大,因此,对不同带宽进行阶跃响应分析,不同带宽下阶跃响应曲线和闭环频率特性曲线如图10、图11所示。
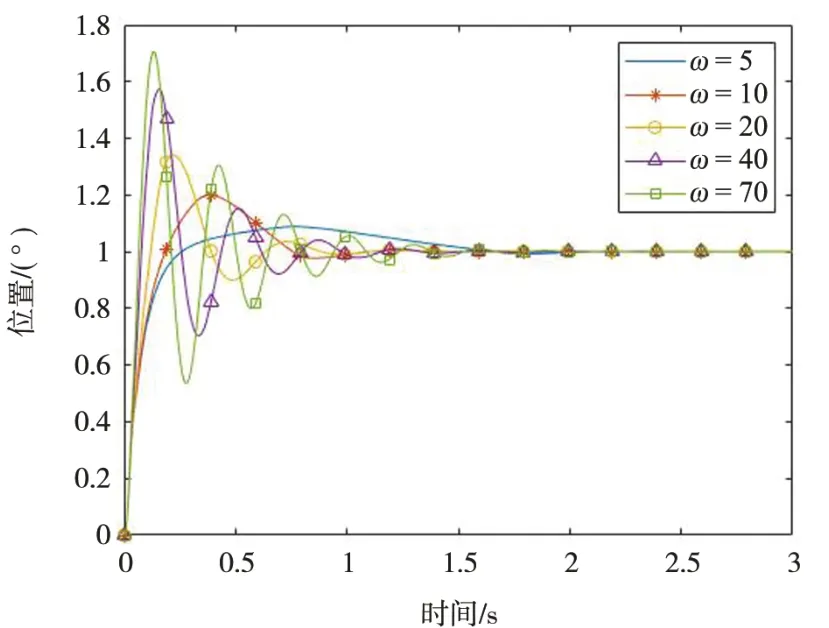
图10 阶跃响应曲线
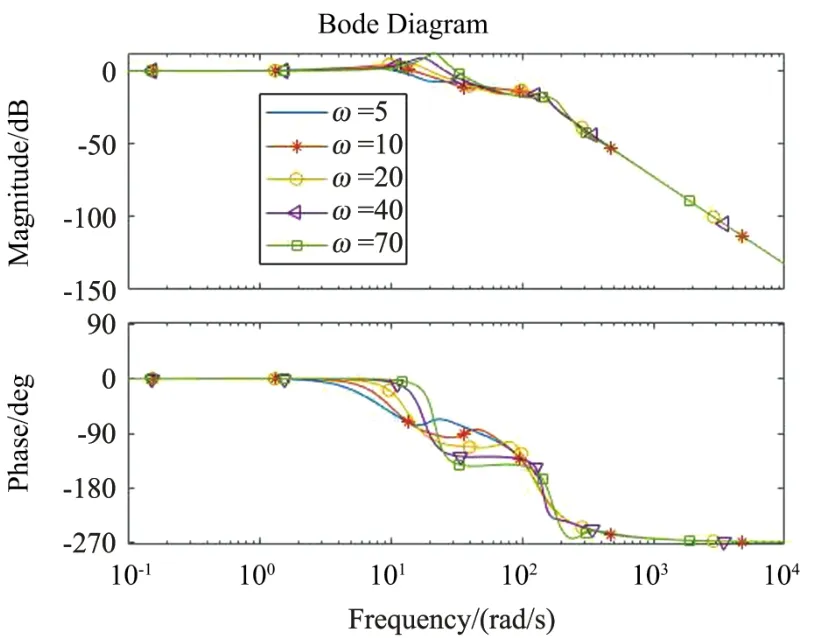
图11 幅频和相频曲线
可以看出在观测器带宽ω0=5时,系统超调量小,但是调节时间过长,从ω0=10开始,随着观测器带宽增大,系统超调量不断增大,调节时间越来越长,逐渐产生震荡,由于加入观测器不断补偿,导致相位裕度逐渐减小,使动态性能下降,调节时间增大。
经过上述对带有扩张状态观测的位置环闭环系统分析,最后选择观测器带宽ω0=20,b=100,Kp=28.59,Ki=169.45,对带有 ESO 的位置环PI控制和不带ESO的闭环控制进行有干扰信号的跟踪精度测试,进一步证实ESO对外界干扰的抑制效果和补偿能力比只有PI控制下好。
进行有干扰的仿真实验,在理想输入阶跃响应1°情况下,在第3 s施加幅值为10°,宽度为1 s的阶跃干扰。如图12为PI和PI+ESO对干扰的抑制效果。传统PI下,最大波动误差为0.54°,而增加了ESO后,波动误差降低为0.215°,说明ESO对阶跃干扰力矩有一定的抑制效果。
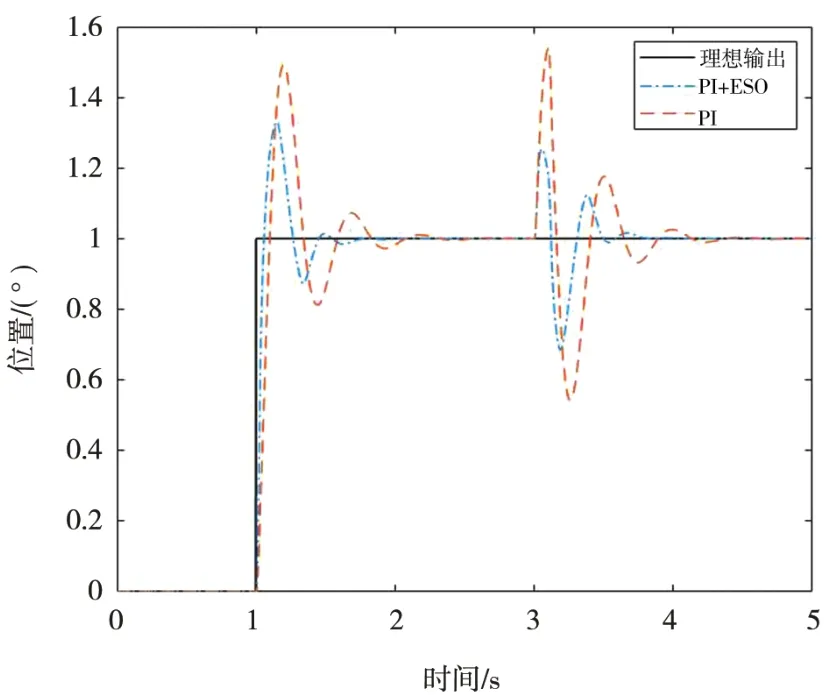
图12 阶跃干扰曲线
同样在相同的阶跃输入下,同时初始施加最大角速度10°/s,角加速度10°/s2的等效正弦θ=10sin(t)°干扰,图13为PI和PI+ESO对干扰的抑制效果。传统PI下,波动最大误差为0.058°,而增加了ESO后,波动最大降低为0.003°,说明ESO对正弦干扰力矩有较好的抑制效果。
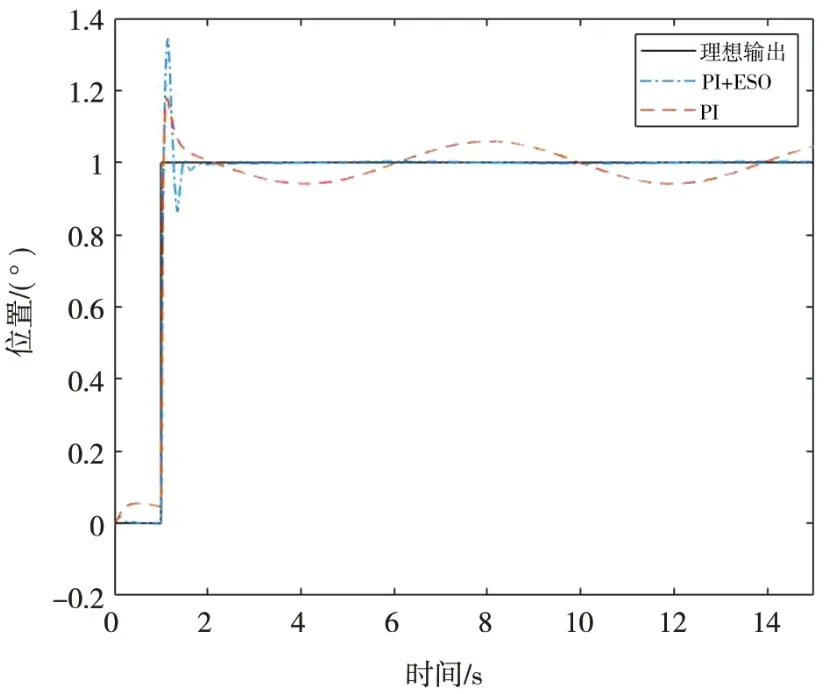
图13 阶跃下正弦干扰曲线
对系统输入1°/s,模拟目标匀速运动,同时输入同等幅值和频率的正弦干扰,模拟车载姿态运动,图14是正弦干扰下的对比曲线。传统PI控制下,稳定后最大误差为0.104 5°,而增加了观测器ESO后,最大误差降低为0.005 386°,跟踪精度提高了19.4倍,说明ESO对正弦跟踪下正弦干扰力矩有较好的抑制效果。
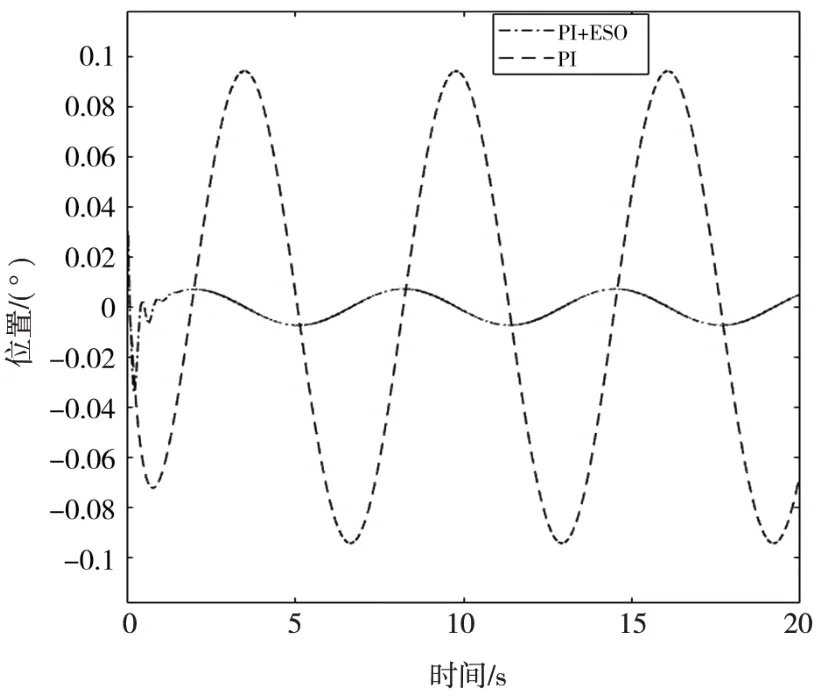
图14 匀速跟踪下正弦干扰跟踪误差
4 实验研究
为测试陀螺速度前馈、PI+ESO在实际车载光电平台上的抗干扰效果和跟踪精度,对实际车载光电跟瞄转台进行测试验证。图15为实验测试场景,在摇摆台上对车载跟瞄转台的方位轴进行测试,对转台进行最大角速度10°/s,角加速度10°/s2的等效正弦引导测试,PI和PI+ESO误差对比曲线如图16所示,设置摇摆台方位按最大角速度10°/s,角加速度10°/s2的扰动作正弦摆动,对远处速度为1°/s匀速运动的平行光管发出的信标光进行跟踪,误差对比如图17所示。

图15 实验测试平台
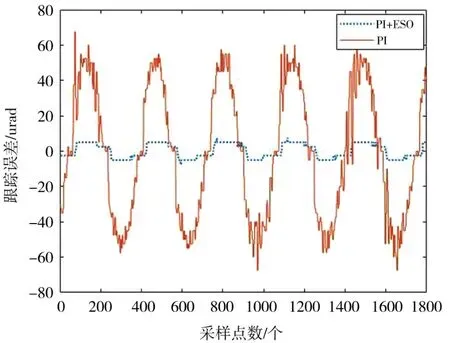
图16 等效正弦引导误差
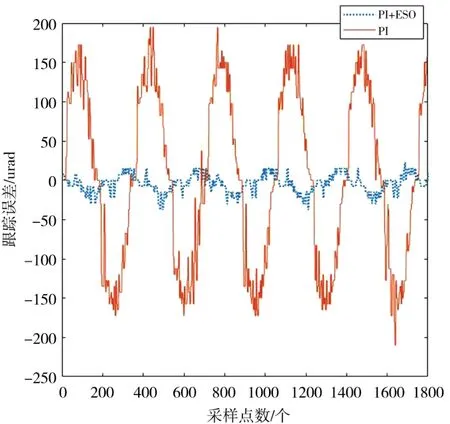
图17 正弦扰动下跟踪误差
在等效正弦引导测试下,应用传统PI的控制算法,转台的正弦引导均方误差为37.33 μrad(1σ),PI+ESO 下的均方误差为 4.13 μrad(1σ),在有扰动的正弦跟踪下,PI控制下转台的跟踪均方误差为111.5 μrad(1σ),PI+ESO下的均方误差为 11.64 μrad(1σ),可以确定引入前馈控制和扩张状态观测器能有效估计和克服平台的扰动并进行补偿。
5 结论
本文针对车载光电平台高精度稳定跟踪问题,采用扰动补偿控制算法,将速率陀螺测得角速度前馈到速度环输入端,通过前馈控制实现对可测扰动的补偿,同时在位置环引用扩张状态观测(ESO),实现对转台位置和未知扰动的实时观测和补偿,并在MATLAB中分别采用PI控制算法和PI+ESO的控制算法,进行Simulink仿真分析,仿真结果证实了速度前馈补偿和PI+ESO的算法具有更小的跟踪误差,在摇摆台上对转台进行最大角速度10°/s,角加速度10°/s2的正弦干扰跟踪测试中,PI+ESO下的跟踪均方误差为11.64 μrad(1σ),跟踪精度相比 PI控制提高 9.58倍。证实了前馈控制和PI+ESO控制算法对抑制扰动和补偿的有效性。
