基于三相变流系统的级联改进自抗扰控制策略

2022-08-26周雪松郭帅朝马幼捷李月超

智慧电力 2022年8期

周雪松，郭帅朝，马幼捷，马闯，李月超

（1.天津理工大学复杂系统控制理论与应用实验室，天津 300384；2.天津理工大学电气工程与自动化学院，天津 300384）

0 引言

能源消费的主要对象为不可再生能源，如石油、天然气等，由于能源消费的持续暴涨，人类生活环境出现了大面积恶化现象。作为缓解能源危机与能源消费的代表国之一，中国提出以“碳达峰、碳中和”为目标的能源政策，为能源转型和向低碳清洁发展开辟了一条光明路径。太阳能具有捕获范围广、清洁程度高、资源无穷多等优点，是当下最具长远应用前景的可再生能源之一[1-3]。光伏系统输出电流不稳是影响系统暂稳态可靠运行的重要因素，为解决电流谐波含量高的问题，选用滤波器进行电流滤波成为当下广泛采用的方法。目前主流做法是将LCL 型滤波器作为滤波装置，以控制经济成本、降低扰动抑制，但其高频段出现的谐振尖峰会使系统在高频下发生谐振，导致并网电流谐波含量激增，引发谐波谐振现象，对系统稳定运行构成威胁[4-7]。

针对由谐波谐振现象而引起的变流系统稳定性问题，国内外专家与学者进行了长时间探索与研究，提出了大量应用价值较高的方法。文献[8-9]最早提出利用实际滤波电阻与滤波电感或滤波电容进行串并联增加系统阻尼的方法，缺点是实际滤波电阻作为耗能元件增加了系统有功损耗、降低了系统经济性。文献[10-12]针对实际阻尼的经济性问题，提出以虚拟阻尼代替实际电阻的方法，分别以电容电压或电容电流作为闭环反馈信号，使重构后的系统自然出现阻尼数值来弥补无源阻尼的不足，缺点是反馈信号的采集和接线会增加系统的复杂性、降低系统的可靠性。文献[13-14]采用基于人工智能的模型预测算法，仅通过编辑程序即达到使系统稳定收敛的要求，但所采用预测算法的核心过于依赖模型，存在大量影响系统运行的不可预测因素，实际应用价值不高。文献[15]以传统比例积分控制算法作为核心算法，通过设置2 个控制器参数达到对系统的稳定控制，缺点是旋转坐标系下的d，q轴系统存在耦合情况，需进行解耦回路的设计，降低了系统的可靠性和经济性。文献[16-17]利用LCL 型变流系统为三阶系统的特性，以线性自抗扰控制（Linear Active Disturbance Rejection Control，LADRC）作为核心控制算法设计三阶自抗扰闭环策略，优点在于计算过程无需解耦，缺点是算法和复杂度极高、工程应用中难度较大。LADRC 是高志强博士在韩京清先生提出的自抗扰控制的基础上进行线性化所得到的[18-19]。LADRC 将系统中拥有不确定特性的因素视作新的状态变量，经线性扩张状态观测器（Linear Extend State Observer，LESO）予以估计量测，最终通过线性状态误差反馈控制器（Linear State Error Feedback，LSEF）给予补偿，成功将原有复杂闭环系统转为积分串联结构系统[20]。LADRC 应用中存在的问题是传统线性自抗扰存在参数间的耦合，会加重系统调参的负担，影响系统的动态性能。

综上所述，本文针对LCL 型三阶变流系统自身谐波谐振现象引起的系统稳定运行问题，设计一种以改进自抗扰和传统自抗扰相结合的双闭环控制策略。通过将三阶系统等效化简为二阶和一阶系统，在一阶系统中引入经解耦重构后的一阶LADRC，在二阶系统中引入传统型LADRC，构成以电流和电压为控制目标的级联双闭环控制策略。最后，通过理论推导与数字仿真，验证了本文所提控制策略的正确性。本文的创新之处在于将新型解耦方法引入双闭环系统中，成功抑制了谐波谐振现象，使系统获得了更为优越的稳定效果。

1 LCL型并网逆变器数学模型

LCL 型并网逆变器结构图如图1 所示。

图1 LCL型并网逆变器结构图Fig.1 Structure of LCL-type grid-connected inverter system

图1 中，L1为逆变器侧滤波电感，L2为网侧滤波电感，C为滤波电容，R1和R2为滤波电感的寄生电阻，UQc为逆变器输出电压，i1abc为三相并网电流，uabc为逆变器输出电压，ucabc为三相滤波电容电压，ugabc为三相电网电压。

根据基尔霍夫电压电流定律，得到LCL 型并网逆变器数学模型为：

式中：i1d和i1q分别为变流器侧电流dq轴分量；i2d和i2q分别为网侧电流dq轴分量；ud和uq分别为逆变器输出电压dq轴分量；ucd和ucq分别为滤波电容电压dq轴分量；ugd和ugq分别为电网电压dq轴分量；ω为系统基波角频率；t为时间变量。

2 一阶改进LADRC设计

2.1 LADRC整体结构

式（1）中，前2 个等式为LCL 型并网逆变器内环系统的数学模型。分别对dq轴设计一阶自抗扰，考虑到dq轴在LADRC 下的数学模型具有一致性，在后续的设计与分析中，仅以d轴模型作为研究对象。一阶LADRC 拓扑图如图2 所示。

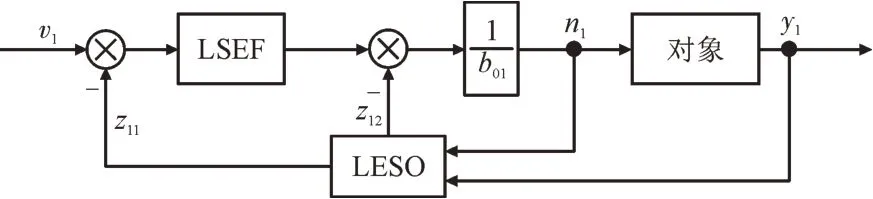
图2 一阶LADRC拓扑图Fig.2 First order LADRC topology diagram

图2 中，LSEF 为线性状态误差反馈控制器，LESO 为线性扩张状态观测器，v1为内环期望信号，b01为内环已知控制增益，n1为内环控制变量，y1为内环输出信号，z11和z12为经LESO 处理后的估计值。

2.2 传统二阶LESO设计

一阶自抗扰系统数学模型为：

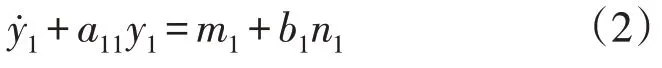
式中：为y1的一阶微分信号；a11为未知系数；m1为内环未知扰动；b1为内环未知部分增益。

令f1=-a11y1+m1+(b1-b01)n1，将式（2）改写为：

式中：f1为内环等效扰动。

令x11=y1，x12=f1，根据LESO 相关理论，可得到传统二阶LESO 的数学模型为：

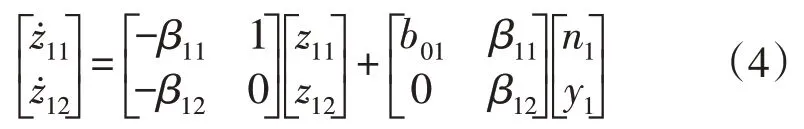
式中：为z11的一阶微分信号；为z12的一阶微分信号；β11和β12分别为z11和z12的二阶LESO 增益。

根据极点配置法理论，将β11与β12配置在可使系统稳定收敛的极点处，二阶LESO 增益表达式为：

式中：p01为二阶LESO 带宽。

2.3 LSEF设计

LSEF 数学模型为：

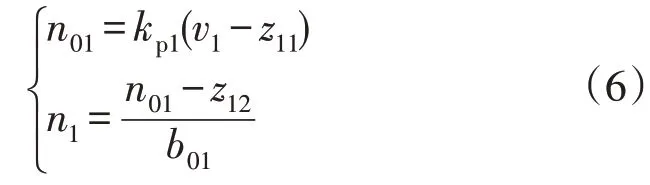
式中：n01为一阶LADRC 等效控制变量；kp1为一阶LSEF 增益。

由极点配置理论，将kp1配置在使系统能够稳定收敛的极点处，一阶LSEF 增益表达式为：

式中：pc1为一阶LSEF 带宽。

根据式（4）和式（6），得到一阶LADRC 的闭环简化数学模型为：

此时复杂闭环系统转为简单积分串联型系统，一阶LADRC 闭环系统结构图如图3 所示，其中，s为拉普拉斯变换算子。

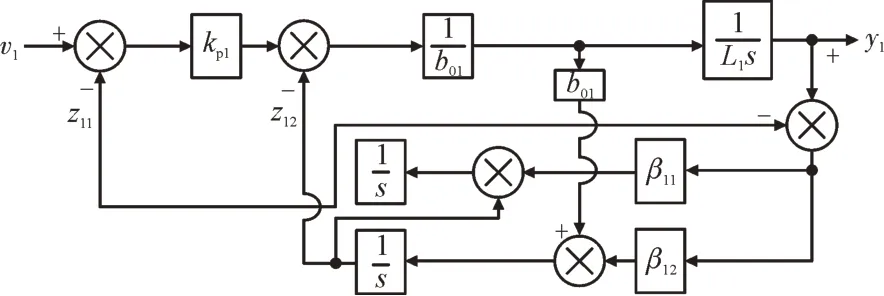
图3 一阶LADRC闭环系统结构图Fig.3 First order LADRC overall structure diagram

2.4 改进型LADRC设计

基于2.1 节-2.3 节对传统LADRC 的设计与分析，可得传统LADRC 的闭环扰动传递函数为：

由式（9）可知，闭环扰动传递函数与p01，pc1均有关，p01与pc1的交链耦合加大了系统调参的难度。为降低系统调参负担并对LESO 进行改进，改进LESO 数学模型为：

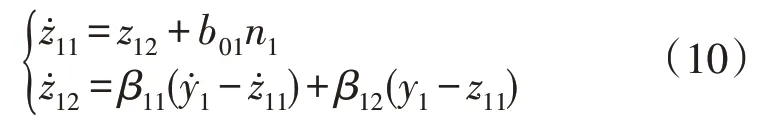
结合式（6）和式（10），可得改进后的LADRC 闭环扰动传递函数为：

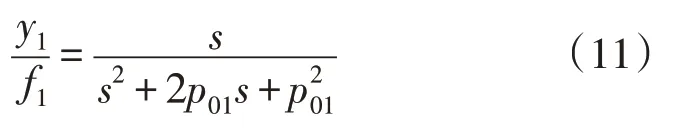
由式（11）可知，此时闭环扰动传递函数仅与p01有关，既规避了其参数耦合的产生，又减轻了调参的负担。为进一步分析传统型与改进型LADRC 之间的优劣，依据2 者扰动传递函数绘制扰动传递函数的伯德图对比如图4 所示。其中，横坐标p为带宽变量，式（5）和式（7）中的p01和pc1均为p的子变量。

图4 扰动传递函数的伯德图对比Fig.4 Comparison of Bode diagram of disturbance transfer function

由图4 可知，改进LADRC 在低频段的幅值特性明显低于传统型LADRC，幅值增益大约相差18 dB，在复杂系统中拥有更优的故障穿越能力。基于式（6）和式（10），绘制改进LADRC 的整体系统结构图如图5 所示。

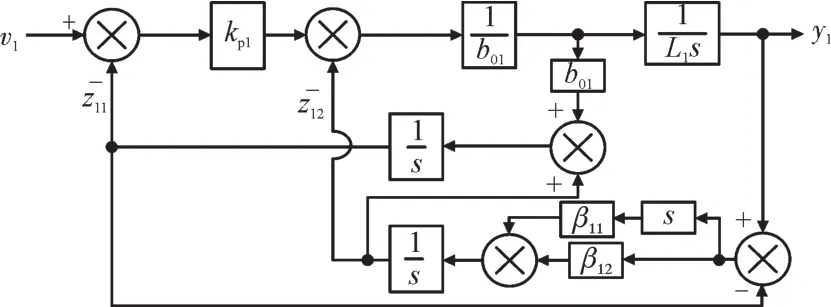
图5 改进LADRC的整体系统结构图Fig.5 Overall system structure diagram of improved LADRC

由图5 可知，与传统LADRC 相比，改进LADRC的接线方式更为简便，提高了系统运行的可靠性与快速性。

3 二阶LADRC设计及级联改进自抗扰策略

3.1 二阶LADRC设计

根据式（1）推导可得LCL 型并网逆变器外环系统的数学模型为：

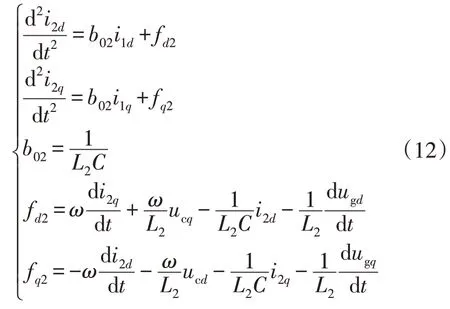
式中：b02为外环已知控制增益；fd2和fq2分别为外环dq轴扰动。

由式（12）可知被控对象为二阶系统，故设计二阶LADRC 策略对其进行控制。二阶系统的一般数学模型为：

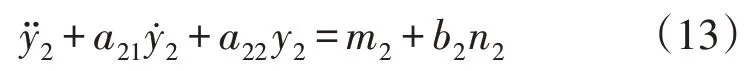
式中：为y2的二阶微分信号；为y2的一阶微分信号；y2为二阶LADRC 输出信号；a21和a22为未知系数；m2为二阶LADRC 未知扰动；b2为二阶LADRC 未知部分增益；n2为二阶LADRC 控制变量。

令f2=-a21y2+m2+(b2-b02)n2，将式（13）改写为：

式中：f2为外环等效扰动。

由式（14）可得二阶LADRC 中三阶LESO 的数学模型为：

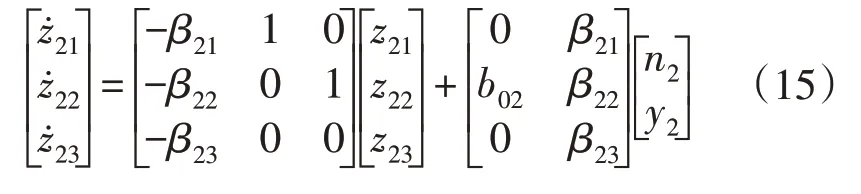
二阶LSEF 的数学模型为：

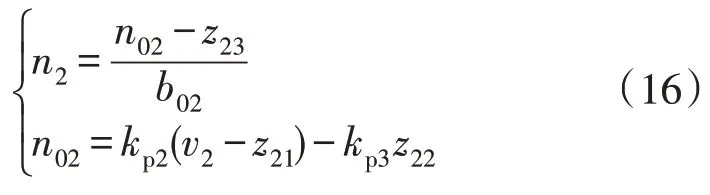
式中：n02为二阶LADRC 等效控制变量；kp2和kp3分别为z21和z22的二阶LSEF 增益；v2为外环期望信号。

根据极点配置法，可得二阶LADRC 的带宽参数为：

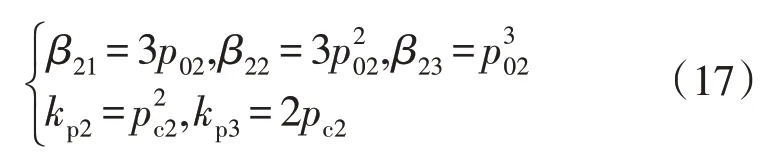
式中：p02为三阶LESO 带宽；pc2为二阶LSEF 带宽。

3.2 级联改进自抗扰控制策略

级联改进LADRC 的整体双环结构图如图6 所示。

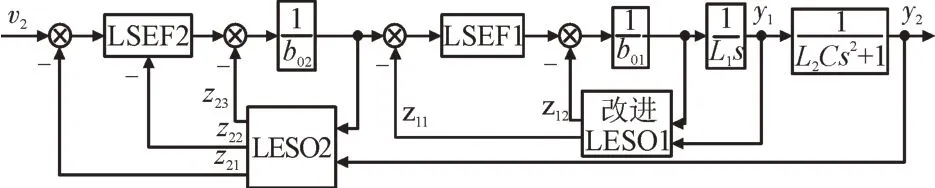
图6 级联改进LADRC的整体双环结构图Fig.6 Overall double ring structure diagram of cascade LADRC

图6 中，LSEF2 为外环线性状态误差反馈控制器，LESO2 为外环阶线性扩张状态观测器，LSEF1为内环线性状态误差反馈控制器，改进LESO1 为内环线性扩张状态观测器。

基于图6 可得级联改进LADRC 闭环传递函数为：

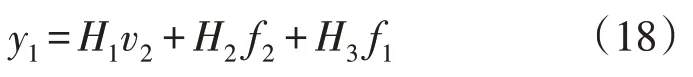
式中：H1为级联改进自抗扰等效期望传递函数；H2为级联改进自抗扰外环扰动等效传递函数；H3为级联改进自抗扰内环等效扰动传递函数。

级联改进LADRC 闭环控制框图如图7 所示。

图7 级联改进LADRC闭环控制框图Fig.7 Closed loop control block diagram of cascade LADRC

由式（18）可知，电流双闭环输出信号由3 部分组成，分别为跟踪指令信号、扰动信号1 和扰动信号2。推导含实际被控对象的闭环传递函数为：

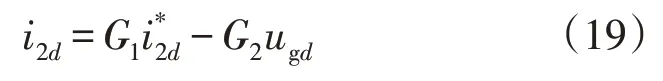
式中：G1为双闭环系统期望传递函数；G2为扰动传递函数。

3.3 级联改进自抗扰策略频率特性分析

分析比较p01，p02，pc1，pc2对LCL 型并网逆变器的影响，从以下4 种情形进行研究[21]。

1）情形1。当pc1为500，p02为15 000，pc2为500 时，p01分别取10 000，20 000，30 000，40 000。情形1 中频率特性如图8 所示。

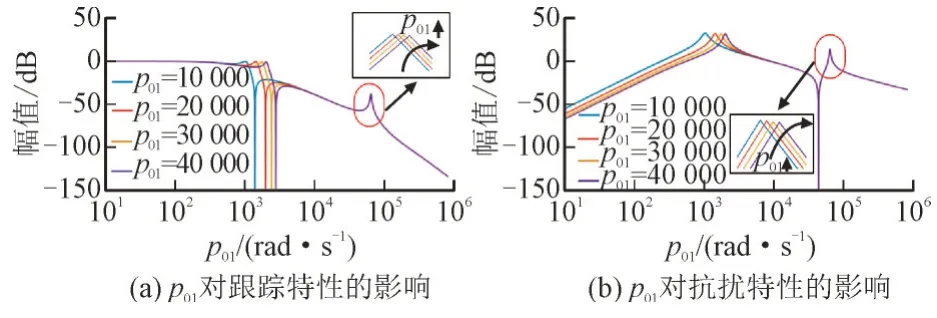
图8 情形1中频率特性Fig.8 Frequency characteristics of case I

由图8（a）可知，随着p01的增加，跟踪特性曲线逐渐向高频段移动（即系统的闭环跟踪带宽得到提高），系统获得更快速的动态响应，高频段几乎处于重合状态。由放大图可知，系统的高频尖峰处于平行状态，且逐渐向右移动。图8（b）中，随着p01的增加，曲线向右移动，高频谐振尖峰几乎重合[22]。

2）情形2。当p01为30 000，p02为15 000，pc2为500 时，pc1分别取100，200，300，400。情形2 中频率特性如图9 所示。

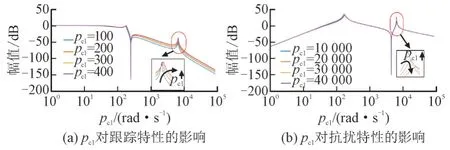
图9 情形2中频率特性Fig.9 Frequency characteristics of case II

由图9（a）可知，随着pc1的增加，系统带宽频率并未发生显著变化，而高频谐振尖峰逐渐被削减，使谐波谐振现象得到了良好的抑制。图9（b）中，随着pc1的增加，由放大图可知谐振尖峰逐渐降低，但降低程度并非明显[23]。

3）情形3。当p01为30 000，pc1为500，pc2为500 时，p02分别取2 000，5 000，8 000，11 000。情形3 中频率特性如图10 所示。

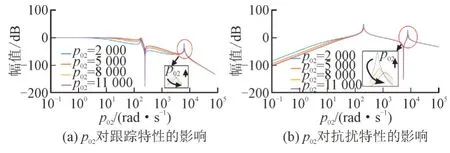
图10 情形3中频率特性Fig.10 Frequency characteristics of case III

由图10（a）可知，随着p02的增加，高频尖峰在向右偏移的过程中逐渐降低，成功抑制了谐波谐振现象。图10（b）中，高频尖峰也随p02的增加逐渐被削减。

4）情形4。当p01为30 000，pc1为500，p02为15 000 时，pc2分别取100，200，300，400。情形4 中频率特性如图11 所示。

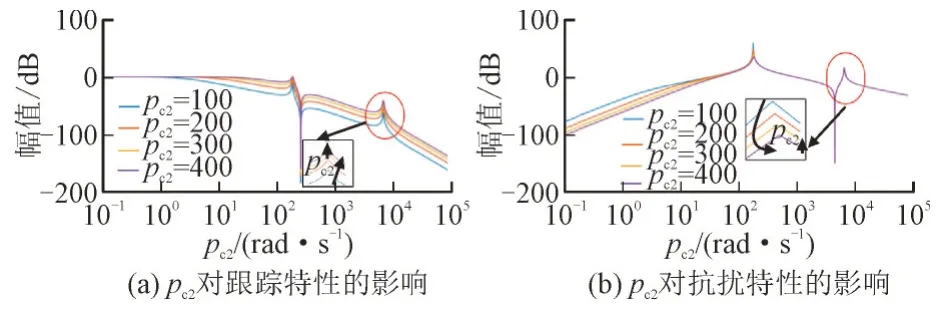
图11 情形4中频率特性Fig.11 Frequency characteristics of case IV

由图11（a）可知，随着pc2的增加，高频谐振尖峰被抬升，逐渐向0 dB 靠近。图11（b）中，高频尖峰被削减，逐渐向0 dB 以下靠近。

4 仿真分析

为验证本文所提控制策略的正确性和时效性，利用MATLAB/Simulink 仿真平台建立了两级三相LCL 型光伏变流系统模型，对本文所提级联改进自抗扰控制策略、传统PI 控制以及三阶LADRC 策略进行比较分析，仿真参数见表1。

表1 仿真参数Table 1 Simulation parameters

4.1 谐振尖峰抑制效果验证

3 种策略下的闭环伯德图如图12 所示。

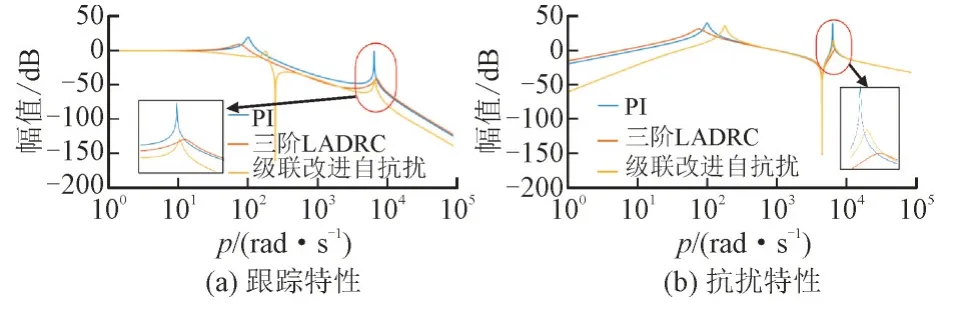
图12 3种策略下的闭环伯德图Fig.12 Closed-loop Bode diagram under three strategies

由图12（a）可知，传统PI 控制下谐振尖峰幅值位于0 dB 附近，当高频段引入噪声信号时，输出波形会出现锯齿状。而在级联改进自抗扰和三阶LADRC 下的高频尖峰幅值位于-50 dB 附近，能有效抑制高频噪声信号。图12（b）展示了对扰动的抑制效果，在低频段级联改进自抗扰几乎位于0 dB 以下，达到了理想了抑制效果，而其余2 种控制方式有较多低频部分位于0 dB 以上，没有级联改进自抗扰抑制扰动能力优越。在图12（b）高频段，PI 下的尖峰幅值靠近50 dB，其余2 种策略均位于0 dB 左右。

4.2 并网电流谐波含量验证

3 种策略下的并网电流谐波畸变率如图13所示。

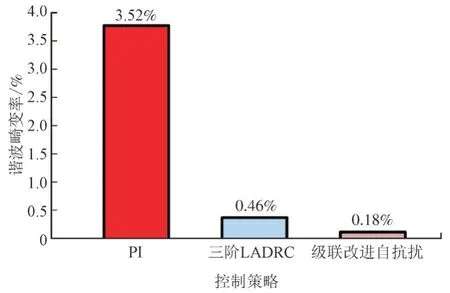
图13 3种策略下的并网电流谐波畸变率Fig.13 Grid connected current TDH under three strategies

由图13 可知，在级联改进自抗扰、三阶LADRC、PI 这3 种控制策略中谐波畸变率分别为0.18%，0.46%，3.52%。由3 种策略对比可知，级联改进自抗扰下的电流谐波抑制效果最好，拥有更好的谐波谐振抑制能力[24-25]。

4.3 dq轴电流起始响应情况验证

网侧dq轴电流波形如图14 所示。由图14（a），（b），（c）可知，级联改进自抗扰下的系统无突变量，三阶LADRC 控制下电流突变量为496.8 A，PI控制下的电流突变量为331.5 A，故在PI 和三阶LADRC 下，系统可能因电流突增导致设备损耗增加，致使经济性降低。级联改进自抗扰、三阶LADRC、PI 的调节时间分别为0.072 s，0.02 s，0.008 s，3 者调节时间并无较大差异[26-28]。由图14（d），（e），（f）可知，级联改进自抗扰电流突变量为80.41 A，三阶LADRC 为132.2 A，PI 为103 A。级联改进自抗扰、三阶LADRC、PI 的调节时间分别为0.05 s，0.036 s，0.02 s，3 者调节时间并无较大差异。基于以上分析可知级联改进自抗扰下的系统拥有更佳的动态响应。