自适应提升及预测误差修正的风电功率超短期预测

2022-08-26谢丽蓉叶家豪乔倜傥

智慧电力 2022年8期

高阳，谢丽蓉，叶家豪，乔倜傥，代兵

（新疆大学电气工程学院，新疆乌鲁木齐 830047）

0 引言

随着全球化新能源的飞速发展[1-3]，具有可持续性、清洁性、储量大的风能被作为主要的新能源。但风资源的不稳定性制约了风能利用率，同时，能否准确预测风电功率对电网的调度计划和风机的安全运行尤为重要[4-7]。

传统的风电功率预测方法大多为物理方法[8]和统计方法[9]。其中，统计方法是根据历史数据规律预测未来数据的发展趋势，方法简单易实现且预测效果较好，但目前集中于研究不同模型的优劣性，集合多个相异模型的亮点，形成组合预测模型[10-13]。与传统预测模型相比，组合预测能够达到更好的预测效果，并且有更强的适应能力[14]。文献[15]用经验模态分解（Empirical Mode Decomposition，EMD）将信号分成信号分量（Intrinsic Mode Functions，IMF），搭建模拟退火（Simulated Annealing，SA）优化的支持向量回归预测模型。文献[16]用集合经验模态将风电功率序列分成IMF 序列采用鲸鱼算法（Whale Optimization Algorithm，WOA）优化最小二乘支持向量机中的超参数，构建预测模型。文献[17]用粒子群算法对极限学习机（Extreme Learning Machine，ELM）参数进行寻优，搭建预测模型，对风速进行预测。文献[18]采用互补集合经验模态分解。在极限学习机的基础上，用改进的布谷鸟算法矫正模型的超参数后，预测处理后的风速序列。这些文献都是针对时间序列的复杂性先分解，针对单个模型的随机参数再寻优，最后预测。然而不同算法及不同的组合模型有其优缺点，如EMD 虽然运算速率快，但是存在分量混叠现象；SA 运行时间短，但全局寻优性差且易受参数影响；WOA 优化速度慢，且不易跳出局部极值等问题。同时大部分组合模型未充分考虑误差来源，继而未进行后处理去修正预测值，造成预测不准确问题[19]。

针对这些存在的问题，本文建立了一种自适应提升及预测误差修正的风电功率超短期预测方法。首先，借助完全自适应噪声集合经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN）把非平稳的功率序列处理成多个平稳子序列，用精细复合多尺度熵（Refined Composite Multi-Scale Entropy，RCMSE）重构子序列，提高预测效率。其次，引入搜索精度高、收敛速度快、稳定性好，并且可避免陷入局部最优的ESSHHO 去优化ELM 参数，在此基础上使用AdaBoost，提高预测精度。最后，基于历史训练误差去预测测试集误差，从而修正预测值，再次提升预测精度。经过验证分析，本文所提预测方法具有更好的预测效果。

1 风电功率数据的分解与重构

1.1 CEEMDAN算法

CEEMDAN 是用于处理非平稳信号的一种算法，是在EMD 算法上的改进算法[20]。

定义Ej(·)为EMD 分解过程中第j个标准正态分布的高斯白噪音；ε0为每次EMD 分解时加入噪音的标准差。CEEMDAN 算法分解的计算步骤为：

1）利用EMD 对信号f(t)+ε0vi(t) 进行R次分解，利用多次相加再均值后消除加入的噪音，即：

2）第1 次分解后的残余量为：

3）利用EMD 算法对r1(t)+ε1E1(vi(t))进行R次分解之后，通过计算平均值，得到第2 个信号分量，即：

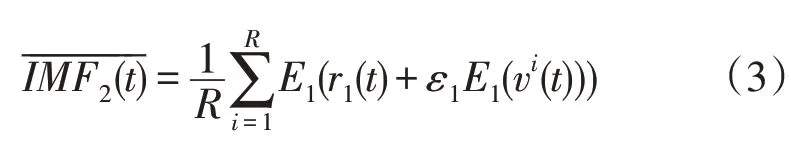
4）对于k=2,···,K，计算第k个残余信号，即：

5）重复步骤3）的计算过程，得到第k+1个信号分量，即：

6）重复4）和5）的分解过程，一直分解到残余分量达到终止条件。则最后的残余量获取式为：

原始信号可由分解信号和最后的残余量得，即：

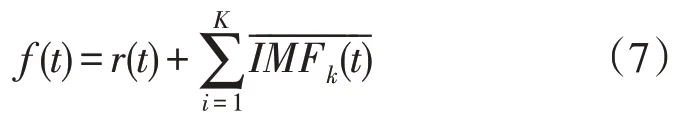
1.2 RCMSE方法

RCMSE 是一种更加有效衡量序列复杂性的度量方法[21]。该方法不仅能够克服其他多尺度熵的未定义熵及熵值不准确问题，而且得到的熵值稳定性更好。其主要步骤如下。

1）对于风电功率时间序列x={x1,x2,···,xn}，其第τ个尺寸粗粒过程为：

式中：m为嵌入维数；r为条件阈值。

2 风电功率预测模型建模

2.1 EESHHO算法

EESHHO 是一种基于哈里斯鹰（Harris Hawks Optimization，HHO）改进的优化算法[22]。该算法将精英进化策略（Elite Evolution Strategy，EES）集成到HHO 的开发阶段，提高了HHO 的局部和全局的挖掘能力以及收敛速度。

EESHHO 算法步骤如下：

1）初始化哈里斯鹰优化算法的种群数量N，最大寻优次数T，哈里斯鹰的位置x，兔子的位置Xrabbit1，Xrabbit2，Xrabbit3和能量E0。

2）计算初始哈里斯鹰的适应度值，确定最优哈里斯鹰个体。

3）根据式（10）计算兔子的自身能量E，如果E大于1，哈里斯鹰处于探索阶段，用探索阶段2 种策略更新哈里斯鹰位置，若E小于1，哈里斯鹰处于开发阶段，用开发阶段的4 种开发策略更新哈里斯鹰位置。

为了模拟从探索到开发的过渡，兔子的能量被建模为：

式中：t为当前的迭代次数；T为最大的寻优次数；E0为猎物初始状态的能量。

4）进行迭代，重复2）和3），不断地更新最佳哈里斯鹰的位置，当寻优次数达到最大寻优次数T时，不再迭代寻优，此时确定适应度最佳的哈里斯鹰及其位置就是优化的最佳结果。

2.2 ELM模型

采用梯度下降法设置神经网络的超参数，具有学习速率缓慢和极难跳出局部最优的缺点，基于此类问题文献[23]提出ELM。该模型在保留泛化性的前提下减少了模型参数选择的计算量。

假设有N个样本集(Xi,ti)∈(Rn,Rm),i=1,2,...,N，其中Xi=[xi1,xi2,...,xin]T，ti=[ti1,ti2,...,tim]T，n为输入维度，m为输出维度。对于单隐含层网络L个隐含层节点可表示为：

式中：αi为输出权值；h(x)为激活函数；Wj为输入权值；bj为隐含层单元阈值。

当输出无误差时，则有：

矩阵形式表达为：

式中：H为隐含层节点的输出；B为输出权值；T为期望输出。

2.3 自适应提升算法

Adaboost 算法是集成算法的一种，其主体思路是多个“弱基学习器”通过集成组合成“强学习器”，从而提升其学习能力。Adaboost 在主体思路下通过有侧重的学习来进一步加强学习能力。侧重表现在关注错误率高的样本，在每次迭代中给错误率高的样本赋于更高的权重，加强对这些错误率高的样本的学习[24]。算法的学习过程如下：

1）把样本数的平均值初始化为训练数据的权值Wt(i)。

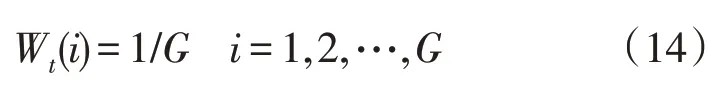
式中：G为训练样本数。

2）弱基学习器预测。通过基学习器对赋予权重的训练数据训练并预测，由此可以得到弱基学习器的预测误差et。

式中：q为弱预测器个数。

3）弱预测器得权重更新。根据式（16）迭算训练样本的权值，调整误差较大的样本权值，使下次能够得到充分地训练。

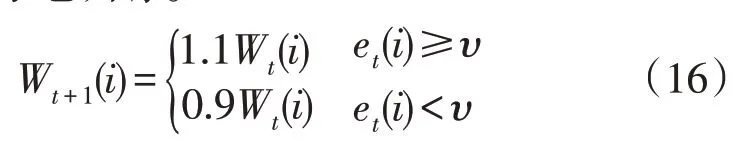
式中：υ为误差阈值。

4）弱预测器的权重计算。根据式（17）更新弱预测器的权值at。

式中：e(t)为弱预测器的预测误差。

5）强预测器预测。采用训练数据训练学习Q次结束。在用弱预测器得出测试集的数据后，根据式（18）计算强预测器预测值Y。

式中：y(t)为t时刻弱预测器预测值。

2.4 EESHHO-ELM-AdaBoost建模流程

ELM 虽然学习速度快，但其输入层和隐含层权阈值具有随机性，这种随机性会造成ELM 训练时间延长，导致预测结果不精确。因此利用EESHHO 对ELM 参数寻优，能提升ELM 的预测精度。同时引入AdaBoost 进一步提高预测精度，提升ELM 的稳定性。建模过程如图1 所示。

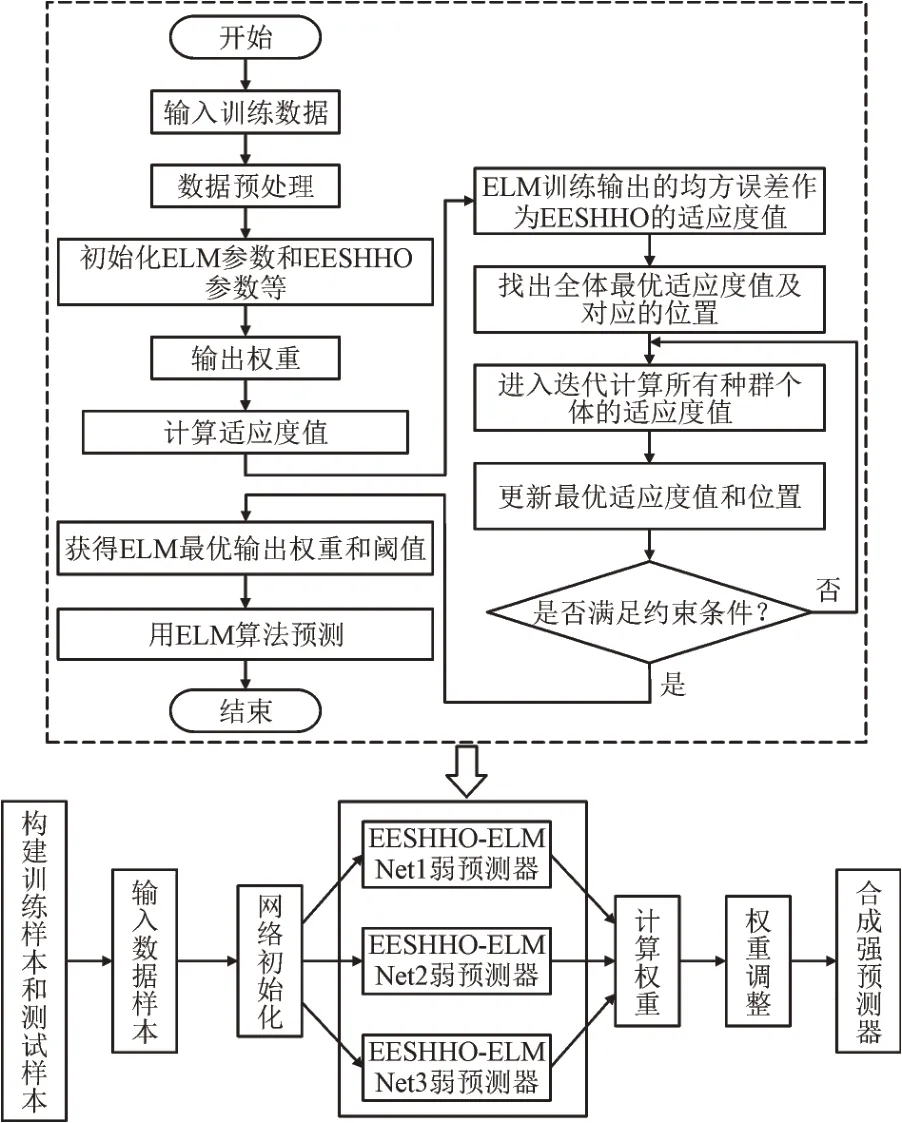
图1 EESHHO-ELM-AdaBoost算法流程图Fig.1 EESHHO-ELM-AdaBoost algorithm flow chart

2.5 预测误差修正

本文在充分考虑风电场数据的不完备性和模型本身的局限性下[25]，建立一种基于训练集误差去预测测试集误差修正预测值的策略。所提策略的预测修正过程为：（1）风电功率预测。用EESHHOELM-AdaBoost 对数据集训练预测得到训练集误差Pe和测试集预测值Pb；（2）误差预测。用模型学习训练集的误差特性，然后用学习好的模型预测测试集的误差序列，得到测试集误差的预测值p′e；（3）计算模型的组合预测值。组合模型的预测值P为测试集的预测值和误差的预测值之和，即

2.6 自适应提升及预测误差修正模型的建模

自适应提升及预测误差修正模型的建模主要流程如下：

1）对复杂的原始风电功率时间序列整理并标准化处理。

2）使用CEEMDAN 有效分解风电功率时间序列，得到本时序分量IMF和残差量。

3）用RCMSE 方法计算熵值，根据近似熵值重构成新IMF。

4）采用EESHHO 算法优化ELM 的权值和阈值，同时使用AdaBoost 集成算法把EESHHO-ELM 弱预测器集合成强预测器。然后预测每个新分量。

5）整合分量的预测值。

6）用学习完训练集误差的EESHHO-ELMAdaBoost 模型预测验证集的误差，从而修正预测值，得到最终的预测值。

自适应提升及预测误差修正模型的建模流程如图2 所示。

图2 基于误差修正的EESHHO-ELM-AdaBoost预测流程图Fig.2 Prediction flow chart of EESHHO-ELMAdaBoost based on error correction

3 实例仿真

本文所用的实验验证数据来自西北地区某风电场，从中截取2017 年1 月1 日到1 月20 日1 832组数据做样本，每隔15 min 采样1 次，共计1 832个采样点，其中前1 800 个当作模型的训练集，剩余的为测试集。天气数据和历史功率作为预测网络的输入层，风电功率作为预测网络的输出。风电功率时序曲线如图3 所示。

图3 风电场功率时序图Fig.3 Wind fam power time series

仿真测试中，EESHHO-ELM-AdaBoost 预测模型的参数设定为：种群规模N=30；最大迭代次数T=500；ELM 输入层为2；隐含层节点个数为8；输出层为1；Sigmod 函数作为激活函数。AdaBoost 弱学习器个数20，误差阈值1.5。

3.1 风电功率数据的处理和分析

对复杂的风电功率时间序列采用CEEMDAN分解，降低复杂度，提高平稳性。CEEMDAN 的噪音组数、噪声标准差和迭代次数分别取50，0.05 和100。风电功率自适应分解结果如图4 所示。

图4 CEEMDAN自适应分解结果Fig.4 CEEMDAN adaptive decomposition result

对分解的IMF分量，用RCMSE 度量其复杂度，从而有效重构分量，提升预测效率及输入特征质量。在计算MRCSE过程中，嵌入维数、条件阈值和时滞分别取2，0.1std(IMFi)和1。每个分量根据近似MRCSE值重构分量结果如图5 所示。

由图5 可知，各分量的MRCSE值主要分布在3.5，2.1，1.2，0.5，0.1 这5 个值附近，为此，重构成5 个新分量，F1=IMF1-IMF3，F2=IMF2，F3=IMF4，F4=IMF5～IMF6，F5=IMF7～IMF11。可以减少模态分量和提高预测效率。

图5 近似MRCSE值重构图Fig.5 Reconstructed graph of approximateMRCSE values

3.2 风电功率的预测实验

为了验证基础模型ELM 的有效性，分析对比了单一模型BP，SVR 和ELM 的预测效果。预测结果对比如图6 所示。

图6 单一模型预测结果对比图Fig.6 Comparison chart of single model prediction results

为了更好地对比验证模型的精确度，使用绝对平均误差（Mean Absoulte Error，MAE）（量值为EMA）和均方根误差（Root Mean Square Error，RMSE）（量值为ERMS）来衡量预测模型的预测精度。

式中：et为t时刻预测的绝对误差值；m为预测采样样本个数。

计算BP，SVR，ELM 3 种单一模型的EMA和ERMS结果，如表1 所示。

表1 单一模型的EMA和ERMS值Table 1 EMA and ERMS of single model

由图6 和表1 可知，ELM 的预测曲线更靠近真实序列，其EMA和ERMS分别是1.384 2 和1.707 0，相比于BP 和SVR 分别提高了13.25%，14.58%和17.38%，29.26%。因此，采用ELM 作为基础预测模型。

分析3 种优化算法AOA，PSO 和EESHHO 优化ELM 权值和阈值后的预测效果，预测效果对比如图7 所示。

图7 优化模型预测结果对比图Fig.7 Comparison chart of optimization model prediction results

分别计算AOA-ELM，PSO-ELM 和EESHHOELM 的评价指标EMA和ERMS值，如表2 所示。

表2 优化模型的EMA和ERMS值Table 2 EMA and ERMS of optimized model

由图7 和表2 可知，EESSHHO-ElM 整体精度较高，整体偏离程度较低，相比于AOA-ELM 和PSO-ELM 来说，在EMA和ERMS上分别提升了3.98%，7.05%和1.07%，1.81%。由此说明，EESHHO 优化的ELM 预测效果更好。

分析对比4 个预测模型的预测效果来验证CEEMDAN 分解和AdaBoost 集成的有效性，预测效果如图8 所示。

图8 模型预测结果对比图Fig.8 Comparison chart of prediction results

4 个模型分别是模型ELM、模型EESHHOELM、模型 EESHHO-ELM-AdaBoost 和模型CEEMDAN-EESHHO-ELM-AdaBoost。

分别计算ELM，EESHHO-ELM，EESHHOELM-AdaBoost 和 CEEMDAN-EESHHO-ELMAdaBoost 的评价指标EMA和ERMS值如表3 所示。

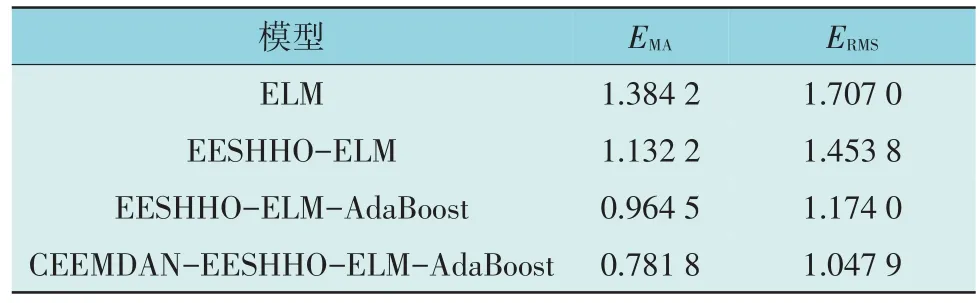
表3 不同组合模型的EMA和ERMS值Table 3 EMA and ERMS of different combined model

由图8 和表3 可知，CEEMDAN-EESHHOELM-AdaBoost 预测效果更佳。在优化预测模型EESHHO-ELM 上引入AdaBoost 集成思想，EMA和ERMS分别提升了16.77%和27.98%。在优化集成模型 EESHHO-ELM-AdaBoost 的基础上加入CEEMDAN 分解，EMA和ERMS分别提升了18.27%和12.61%，达到0.781 8 和1.047 9。因此，验证了加入AdaBoost 和CEEMDAN 能够有效提高预测精度。

利用训练集的训练相对误差序列去预测测试集的相对误差序列，用来修正模型的初始预测值，更进一步提升模型的预测效果。误差修正预测结果对比如图9 所示。

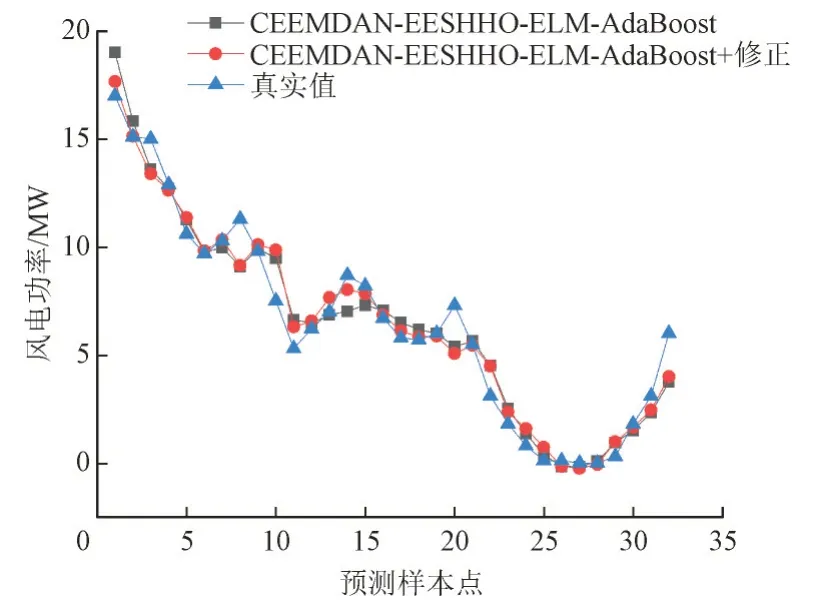
图9 误差修正预测结果对比图Fig.9 Error correction prediction results comparison chart

计算对比分析修正之前和修正之后的EMA和ERMS值。修正之前和修正之后的EMA和ERMS值如表4 所示。

由图9 和表4 可知，与未修正的预测模型相比，修正后的预测模型达到了更高的预测精度。EMA和ERMS分别提高了10.1%和8.59%，由此可知，根据训练集训练误差去预测测试集误差从而修正预测值能够有效提高预测精度。

表4 误差修正模型的EMA和ERMS值Table 4 EMA and ERMS of error correction models

为进一步测试本文所提模型应对非平稳数据的预测性能，增加预测时间尺度。对比了以ELM 为基础，逐层引入EESHHO 优化、AdaBoost，CEEMDAN分解和误差修正5 种模型的预测结果如图10所示。

图10 5种模型预测结果对比图Fig.10 Comparison of prediction results of five models

从图10 可知，CEEMDAN-EESHHO-ELMAdaBoost+修正的预测曲线更接近真实功率曲线。为了更加清楚预测性能提升程度，分别计算5 种预测模型的评价指标EMA和ERMS的值，如表5 所示。

表5 5种预测模型的EMA和ERMS值Table 5 EMA and ERMS of five prediction models

由表5 可知，CEEMDAN-EESHHO-ELMAdaBoost+修正的模型预测效果最好。与CEEMDANEESHHO-ELM-AdaBoost 相比，EMA和ERMS分别提高了10.17%和5.62%；与EESHHO-ELM-AdaBoost 相比，EMA和ERMS分别提高了20.02%和52.02%；与EESHHO-ELM 相比，EMA和ERMS分别提高了67.08%和117.68%；与ELM 相比，EMA和ERMS分别提高了269.88%和574.68%。由此可得，本文所提的预测方法预测性能更佳。