双馈风电机的虚拟惯性控制优化策略
2022-08-26杨德健金恩淑郑太英金朝阳
王 鑫,杨德健,金恩淑,郑太英,金朝阳
(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林吉林 132012;2.浙江大学电气工程学院,浙江杭州 310058;3.电网智能化调度与控制教育部重点实验室(山东大学),山东济南 250061)
0 引言
双馈风力电机(Doubly-fed Induction Generator,DFIG)具有“变速恒频”等优良性能,其通过变流器并网实现了转子与电网进行功率交换的功能,但导致DFIG 转子转速与系统频率解耦,造成整个系统的惯性响应能力降低[1-2]。在系统面对扰动时,DFIG 并不能像同步机一样参与调频,导致频率大幅跌落[3-4];随着风电渗透率的不断增加,频率跌落会愈发严重,容易启动低频减载保护,甚至导致系统崩溃[5-6],如英国“8.9”大停电、我国锦苏直流闭锁等[7]。为此,众多国家要求DFIG 具有一定的调频能力,并为此提供相应的奖励政策[8-10]。
DFIG 参与系统调频能量来源可分为:外部储能、功率备用和风机转子动能,其中储能需要增设设备,能量管理和转化较为复杂,增加调频成本[11-14];以功率备用作为能量来源的超速控制和桨距角控制均降低了风能利用率,不利于DFIG 经济运行[15];以风机转子动能为能量来源的虚拟惯量控制(Virtual Inertia Control,VIC)方法,获得良好的调频效果,专家学者们对此展开了大量研究[16-19]。
文献[20]中根据DFIG 的控制特点和控制过程,通过附加惯性控制环节,使DFIG 能够在一定程度上参与系统频率调整,然而使用虚拟惯性控制的固定控制增益不能充分利用转子动能。文献[21]中研究了风电机组在不同控制增益下虚拟惯性控制性能。为进一步提高系统频率稳定性,文献[22]提出使用最大频率偏差变化率进行虚拟惯性控制,但DFIG 运行时很难准确测量最大频率变化率。文献[23] 基于风电机组比例微分(Proportional-Derivative,PD)虚拟惯性控制的基本原理,推导了PD 虚拟惯量控制与系统频率的量化关系,分析表明微分系数主要影响频率跌落速度,对频率跌落最低点影响较小。
为此,本文提出计及频率偏差的虚拟惯性控制策略,通过将传统虚拟惯性控制中控制器增益与频率偏差建立耦合关系,从而使DFIG 在面对不同扰动调整调频增发功率,充分利用自身转子动能参与调频,实现调频的目的。最后在EMTP-RV(Electro Magnetic Transient Program-Restructured Version)仿真平台搭建了电力系统模型,验证改进策略的有效性。
1 DFIG结构及惯性响应机理
1.1 DFIG的主要结构
本文以DFIG 为研究对象,主要由风轮机、齿轮箱、感应电机和变流器组成,如图1 所示。
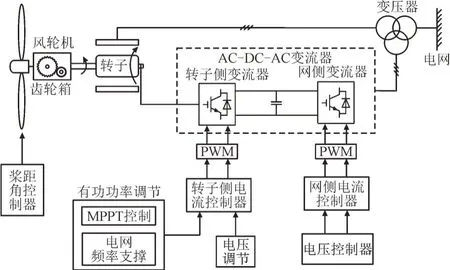
图1 典型双馈风力发电机组及控制系统示意图Fig.1 Diagram of typical DFIG and control system
其中,MPPT 控制为DFIG 的最大功率跟踪控制(Maximum Power Point Tracking,MPPT),PWM 为一种脉宽调制技术(Pulse Width Modulation,PWM)。
风机输出的机械功率Pm可用式(1)描述:

式中:CP(λ,β)为风能的捕获效率;s为风机叶片扫过的面积;vw为风速;ρ为空气密度。
CP(λ,β)与叶尖速比、风机桨距角、风速的关系式如下:
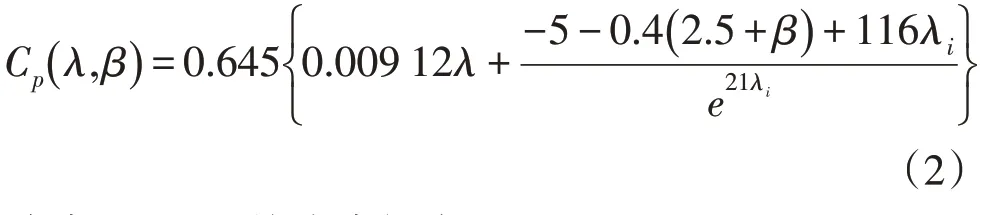
式中:λ,λi均为中间变量。
λ,λi表达式如下:

式中:ωr为风机的转子转速;β为风机桨距角。
为了使风电机组在不同风速下,风能得到充分利用,DFIG 运行在MPPT 控制。
1.2 DFIG惯性响应机理分析
DFIG 含有丰富转动惯量,其更加宽泛的转速调节范围,使其利用自身转子动辅助调频变为可能[24-25]。仿照同步发电机对DFIG 建立惯性时间常数表达式如下:

式中:H为DFIG 惯性时间常数;J为转子惯性系数;ωn为DFIG 额定转速;S为额定容量。
将式(5)代入转子运动方程中,并标幺化处理得:

式中:ΔPpu为扰动的标幺值;ωr.pu为转速的标幺值。
对式(6)积分,并且用频率标幺值代替转速标幺值,可得到式(7):

式中:t0为扰动发生时刻;为t0时刻系统频率标幺值;Δt为时间间隔;ΔEpu为DFIG 惯性响应期间释放动能的标幺值;为(t0+Δt)时刻系统频率。
由式(7)可知,DFIG 可通过模拟惯性响应释放转子动能,协助同步机调频;DFIG 释放的动能与系统频率存在密切关系,即DFIG 释放动能ΔEpu越大,根据能量守恒原理可知,同步机组转子吸收能量越多,频率最低点改善效果越好。
2 DFIG调频策略
2.1 DFIG传统惯性控制
在扰动期间,为了使DFIG 模拟同步机惯性响应,给电网提供频率支撑,提出了虚拟惯性控制,DFIG 输出的有功功率Pref如下:

式中:PMPPT为MPPT 输出参考值;PA为虚拟惯性控制中抑制系统频率跌落的调频增发功率;K为控制增益;fpu为系统频率标幺值。
以式(8)和式(9)为基础建立传统虚拟惯性控制框图,如图2 所示。其中,f为系统频率,fnom为系统频率标准值,T为滤波器时间常数。

图2 传统虚拟惯性控制框图Fig.2 Traditional virtual inertial control block diagram
扰动期间,DFIG 按照式(9)约束,随频率变化率的变化增加输出功率,释放自身旋转动能,为系统提供频率支撑。
由文献[26]可知,传统虚拟惯性控制可以改善最大频率变化率,但对频率最低点的作用很小,主要是因为如式(9)所示PA在短时达到最大值之后会迅速减小,并在频率最低点减小至0。此外,由于传统虚拟惯性控制中控制参数恒定不变,在不同扰动情况下会限制DFIG 参与调频能力。故要如何使DFIG 在不同扰动下发挥更好的调频能力(频率跌落和频率变化率)是值得探讨的问题。
2.2 基于系统频率偏差的惯性控制改进策略
针对如何更好发挥DFIG 调频能力的问题,本文提出了基于系统频率偏差的改进虚拟惯性控制方法,如图3 所示。
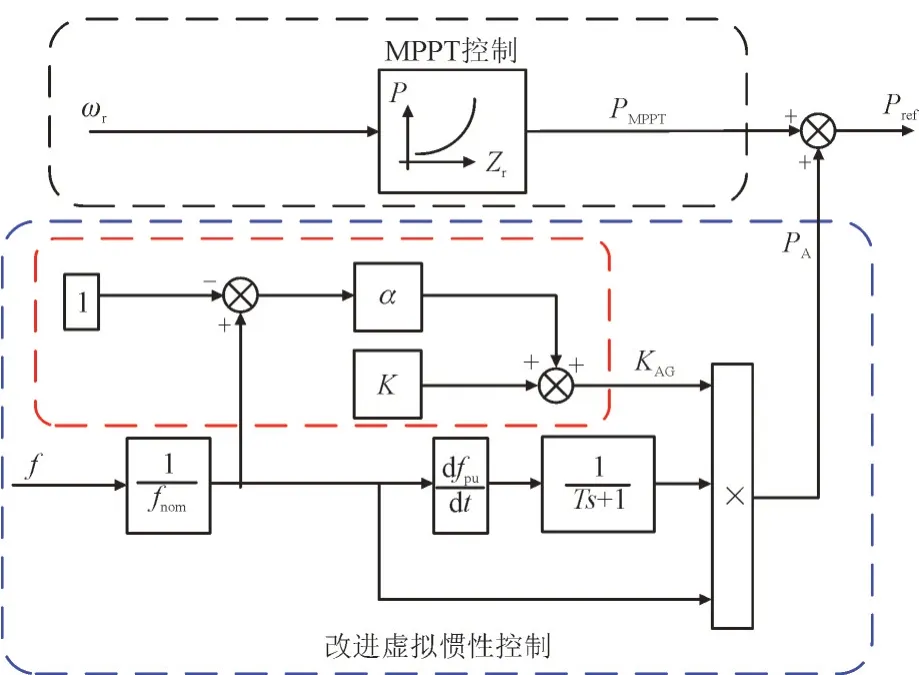
图3 改进虚拟惯性控制框图Fig.3 Improved virtual inertial control block diagram
改进虚拟惯性控制的补偿功率表达式如下:

式中:KAG为改进的控制增益;Δf为频率偏差;a为修正系数。
由式(10)和式(11)可知,KAG与系统频率存在耦合关系,扰动初期,Δf很小,KAG近似等于K,改进虚拟惯性控制与传统虚拟惯性方法输出的增发功率几乎相同。
由式(10)和式(11)建立补偿功率与频率变化率及频率偏差的三维图像,如图4 所示。

图4 补偿功率与频率变化率及频率偏差的曲线图Fig.4 Curve of compensation power and frequency change rate and frequency deviation
由图4 可知,随着Δf增大,KAG增大,Δf成为KAG的决定性因素,即频率变化率大幅减小,DFIG 能在系统频率变化率变为0 前提供更多的功率,有效地改善最大频率偏差。此外,在不同扰动下,DFIG 可灵活地为系统提供功率补偿,输出更多调频增发功率,减缓频率跌落速度,提高频率最低点。
由参考文献[9-10]可知,DFIG 参与调频的调频增发功率经济效益C为:

式中:CA为虚拟惯量响应补偿标准。
由式(12)可知,调频增发功率与其带来的经济效益成正比。在同样扰动下,相比于传统虚拟惯性控制,本文提出的改进虚拟惯性控制方法可为系统提供更多的调频功率,进而可获得更多调频效益。
3 基于EMTP-RV平台仿真分析
3.1 仿真系统模型
为了验证提出的改进虚拟惯性控制方法的有效性,在EMTP-RV 仿真平台上建立高风电渗透率的电力系统模型,包含6 台同步发电机SG1—SG6、1 个DFIG 聚合风电场、1 台异步电动机和容量为350 MW 的静电荷,其中DFIG 聚合风电场由20 台5 MW 的DFIG 组成。电力系统模型的结构图如图5 所示。
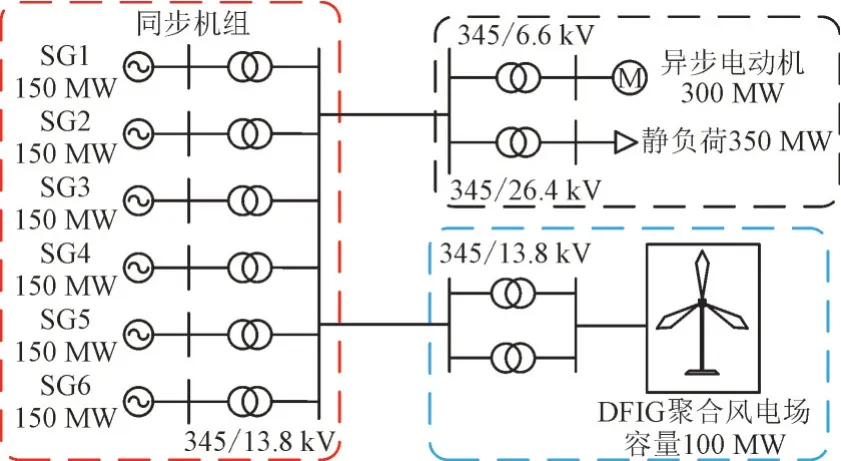
图5 仿真系统模型Fig.5 Model of simulation system
3.2 控制方法仿真对比
本文采用控制变量法来进行验证改进虚拟惯性控制的有效性,在恒定风速下建立扰动分别为70 MW 和110 MW 其他条件都相同的情况,对MPPT、传统惯性控制策略、改进惯性控制策略(a=100,a=200)的控制结果进行分析。
1)算例1:恒定风速9 m/s,扰动70 MW。
算例1 的仿真结果如图6 所示。在图6 中,同步机SG1在50 s 时脱网,造成70 MW 的功率缺额。当DFIG 以MPPT 运行时,频率变化率最大可达0.402 Hz/s,频率跌落至59.346 Hz;采用传统方法时,DFIG输出一定的补偿功率(能量来源于风机转子动能释放),频率跌落程度和频率跌落速度得到改善;采用本文提出的优化方法时,DFIG 能提供更多调频功率,不仅改善频率最低点和频率跌落速度,协助同步机调频,并且提高了风电场的调频收益。
由图6 可知,在改进虚拟惯性控制方法中,通过适当增大KAG中的修正系数α,可提高DFIG 对频率偏差的灵敏度,提供更多调频功率,获得更好的调频效果、更多调频收益。
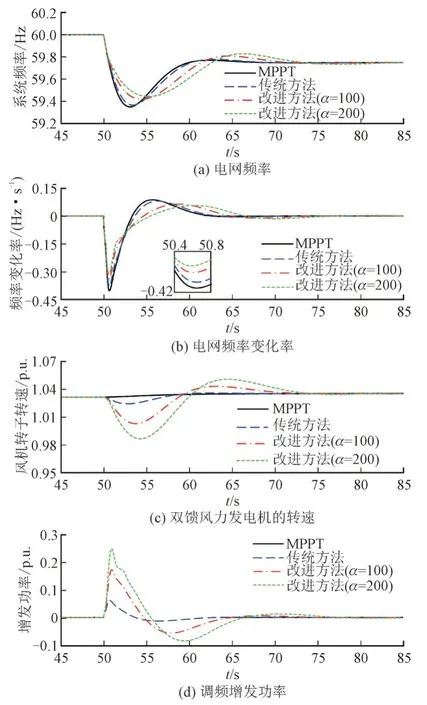
图6 算例1的仿真结果Fig.6 Simulation results of case 1
2)算例2:恒定风速9 m/s,扰动110 MW。
当系统功率缺额达到110 MW 时,仿真结果如图7 所示。

图7 算例2的仿真结果Fig.7 Simulation results of case 2
从图7 可以看出,在扰动增加40 MW 时,系统频率跌落更严重,频率最低点为58.938 Hz。在采用本文提出的优化方法后,DFIG 能大幅增加调频输出,短时调频功率最大值达至0.358 p.u.,频率最低点升至59.08 Hz,与传统虚拟惯性控制方法相比,对频率改善效果更好,风电场获得的调频收益多。
综合算例1 和算例2 可知,随着扰动增大,DFIG 采用改进虚拟惯性控制输出的调频增发功率与采用传统方法输出的调频增发功率之间的差值增大,不仅能使系统频率跌落得到大幅改善,风电场还能通过协助调频服务获得更多收益。
3)算例3:随机风速,扰动110 MW 功率。
为了更加贴近现实中DFIG 运行情况,使风机在50 s 产生110 MW 的功率缺额后,风速随机变化[26](在扰动前DFIG 进行初始化,保持风速恒定)。算例3 的仿真结果如图8 所示。

图8 算例3的仿真结果Fig.8 Simulation results of case 3
从图8 可以看出,与算例1 和算例2 相似,改进虚拟惯性控制能够在随机风速情况下,输出更多补偿功率,减缓频率跌落速度,提高频率最低点。
结合3 个仿真算例可知,本文所提改进虚拟惯性控制方法能更好地利用风机旋转动能参与调频。3 个算例汇总图如图9 所示。由图9(a)可知,从系统调频角度出发,本文提出方法频率跌落小,跌落速度慢,且扰动越大,调频效果越显著;由图9(b)可知,在风电场调频收益方面,本文提出方法比传统提供更多调频增发功率,风电场协助同步机调频获得的收益更高。并且通过适当增加增益系数中α的值,使DFIG 协助调频效果更好,给风电场带来更多的经济效益。
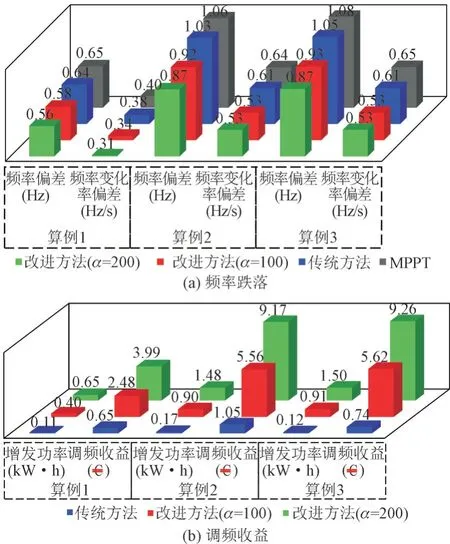
图9 算例总结Fig.9 Case summary
4 结论
本文针对DFIG 系统调频能力受限的问题,提出了计及频率偏差的虚拟惯性控制增益,改进后的虚拟惯性控制策略的创新点如下:
1)从系统调频角度出发,在控制增益中引入频率偏差,使其控制增益系数能够根据系统当前状态进行实时调整,输出更适合当前工况调频增发功率,改善频率跌落最低点及频率跌落速度。
2)从风电场收益角度出发,控制增益与频率偏差建立耦合关系,DFIG 能输出更多调频功率,获得更多调频收益。
3)通过调节修正系数α可以增加系统对频率偏差的灵敏度,增强DFIG 的调频效果,带来更多调频收益。
