反复多次通过方法中角动量对重核熔合的影响
2022-08-25苗泽宇
刘 玲, 苗泽宇, 刘 旭
(1. 沈阳师范大学 物理科学与技术学院, 沈阳 110034;2. 辽宁教育学院 基础教育教学研究中心, 沈阳 110032)
0 引 言
近年来,合成超重核是核物理研究的热点问题,原子核物理结构理论预言[1-2]双幻核208Pb后,下一个出现的双幻核的中子数N=184,质子数Z=114,在这附近会存在一批长寿命的新稳定核素,即“超重核稳定岛”。合成超重核对探究原子核质量极限有重要意义,重离子熔合反应是目前合成超重核的唯一途径。对于近似对称的弹靶熔合反应系统,两质子数符合Z1*Z2>1 600,且接触位置在条件鞍点之外时,弹靶熔合后会形成激发态的复合核,蒸发中子后形成超重核[3]。
目前,人们广泛应用Langevin方程[4-5]对弹核、靶核的熔合过程进行描述。原子核变形运动的动力学过程与布朗粒子的扩散运动相类比,如果把核内核子的运动作一个热浴处理,将单粒子自由度与变形自由度耦合来比为介子对布朗粒子的碰撞,通过解合适的Langevin方程就可以模拟布朗粒子随时间的演化过程,并追踪熔合的轨道[6]。在以往的Langevin模拟中,一旦一条Langevin轨道(试验粒子)到达鞍点,则认为熔合事件已发生,便停止对该轨道的追踪,称之为定义在鞍点处的首次通过条件鞍点模型[3-11]。然而一个粒子跃过条件鞍点后在热涨落的作用下,可能会再次返回条件鞍点,在鞍点处形成反复运动,引起所谓的回流效应[12-14],热涨落越强烈,回流也越强烈。通过记录粒子最后一次通过条件鞍点的时间来定义在鞍点处的通过几率,称之为试验粒子反复多次通过条件鞍点模型[3,6-7]。粒子最终到达基态位置,记录到达基态位置的时间,可以定义在基态位置处的通过几率,称之为基态位置的模拟模型,这在以往的研究工作中较常见。
对于利用反复多次通过鞍点模型讨论核裂变与熔合的相关课题较多,但均未考虑角动量这一因素的影响。而在实际物理问题中,重核熔合是一个复杂且困难的过程,角动量的影响是十分重要的,超重核合成的大部分理论研究均要考虑角动量的作用。本文在原有工作基础上加入角动量,主要利用反复多次通过条件鞍点模型来研究角动量对核熔合的通过几率的影响;研究并分析在不同的角动量下,通过几率的变化机制;在考虑角动量的前提下,进一步探究温度、入射能量对通过几率的影响。
1 以前研究中的理论方法
描述重核熔合动力学过程通常可以用朗之万方程来描述,两熔合核的质心距q(t)随时间变化为
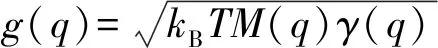
把随机龙格—库塔方法和单步迭代方法结合来求解方程(1)和(2),既能避免产生高阶导数,精度也比较高。朗之万方程组的数值解为
式中
其中:q*(t)和v*(t)为单步迭代方法的模拟解;Ψ表示均值为0,方差为1的标准高斯随机数[15-16]。
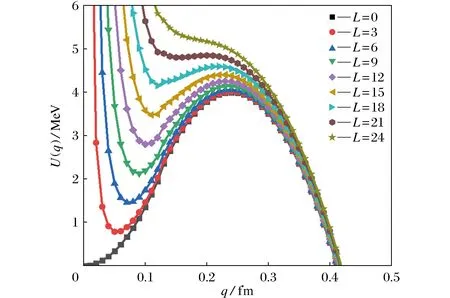
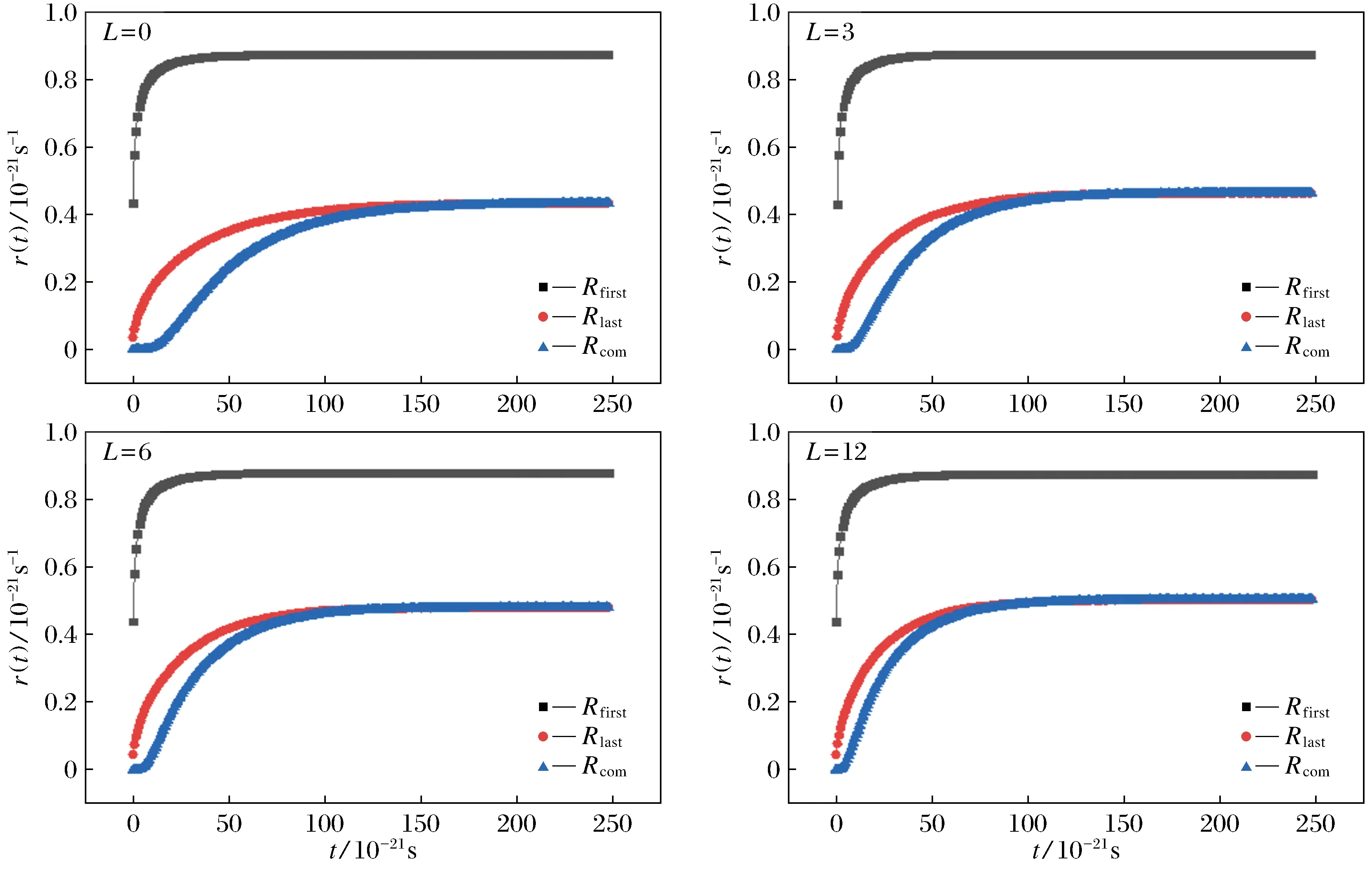
一般情况下,当布朗粒子的坐标在鞍点位置之前,即q(t) (7) 其中:N(t)表示t时刻未熔合的粒子数; dN(t)表示从t到t+dt内发生熔合的粒子数。为统计方便,规定一个有限时间间隔ts,在t~t+ts内平均通过几率为 (8) 未考虑角动量前,考虑一个正谐振子与一个倒谐振子光滑链接的复合核形变位势[8],熔合势垒可表示为 (9) 鞍点位置qb=0.24 fm,势垒高度Vb=4 MeV,基态位置q0=0 fm,其他参数m0=376.3ћ2MeV-1fm-2,时间步长τ=4/Tћ2/MeV,约化粘滞系数β=γ/m=464.4T2MeV/ћ[4]。 加入角动量后的熔合势垒的形式如下: 其中公式(11)取自文献[17-18]。为计算方便,将公式(11)的分子分母同时乘以c2, 已知ћc=197.327 053[MeV·fm],μ=931.494 32[MeV/c2]。本文研究的是248Cf[10]复合核的熔合过程,所以令带入计算的质量μ=248μ。为了使基态位置势阱更明显,引入常量A=900,所以公式(11)分母中的μ值应该为μ=248 Aμ。 为探究角动量与复合核位势的关系,根据式(10)和(11)得到图1。由图1可知,加入角动量以后,基态位置不再是q0=0 fm,随着角动量的增大,基态位置的坐标(横坐标)在向右移动,基态位置与条件鞍点的距离变得越来越近,模拟粒子更容易到达基态位置。条件鞍点左侧的势阱也随角动量的增大而变浅,大约在临界值L=21附近势阱消失了,没有势阱也就没有了束缚态,这说明此后的角动量对研究重核熔合的影响极小。然而角动量对于条件鞍点以外的势垒形式(0.35 fm~0.45 fm)影响很小,只比没有角动量的情况有轻微的提升。另外,条件鞍点所对应的势能高度也随着角动量的增加而增加。而条件鞍点变高效应,使模拟粒子不易通过条件鞍点。由式(10)和(11)可知,随着角动量的增加,体系的总能量变大,这有利于模拟粒子通过条件鞍点。这3种效应的共同竞争作用决定最后重核熔合过程的通过几率。 图1 加入角动量复合核位势随相对位置的变化Fig.1 Variation of compound nuclear potential with relative positions by adding angular momentum 图2是相同温度(T=4 MeV)同一入射能量(Ec.m.=7.526 MeV)下,不同角动量(L=0,3,6,12)下通过几率随时间的演化。方块曲线代表首次通过条件鞍点模型的结果,圆圈曲线代表反复多次通过条件鞍点模型的结果,上三角曲线代表定义在基态位置模拟模型的结果(模拟粒子为20 000个)。从图2中可以观察到,3种模拟方法在短时间内均到达稳态值,在不同角动量下,首次通过的结果均远远高于其他2种结果,首次通过模型的通过几率也更早到达稳态值。这是因为在首次通过条件鞍点模型中,在热涨落的作用下,一部分试验粒子掉落到断点发生裂变,而其他试验粒子一旦越过条件鞍点便认为熔合完成,形成复合核。而实际上首次通过模型中已经通过条件鞍点的试验粒子在热涨落的作用下很可能又返回条件鞍点,并在条件鞍点形成反复多次运动,引起所谓的回流效应,迟滞了粒子到达基态的时间,从而可以减小最终的通过几率。而记录最后一次通过条件鞍点时间的反复多次通过条件鞍点模型充分考虑了这一现象,并且能够发生最后一次通过条件鞍点的粒子事件就一定能够到达基态位置,因此,把最后一次通过鞍点的时间用来定义、统计鞍点处的通过几率显然也比定义在基态位置的通过几率更合理。从图2中可以看到,反复多次通过方法大大降低了首次通过方法的稳态值,而由于最后一次通过鞍点时间与到达基态位置的时间很短,所以反复多次通过方法和定义在基态位置的通过几率的稳态值很接近。而图2中不同角动量的加入并没有影响这3种不同模拟方法通过几率的稳态值的特点。但继续观察发现:考虑角动量后对首次通过条件鞍点模型的通过几率瞬态行为几乎无影响,而明显影响反复多次通过条件鞍点以及定义在基态位置的瞬态过程通过几率的差值,随着角动量的增加,瞬态差值明显变小,它们的瞬态行为更为接近。 图2 不同角动量下通过几率随时间的演化Fig.2 Evolution of passing probability with time under different angular momentum 图3 不同入射能量下,通过几率随角动量的变化Fig.3 Variation of passing probability with angular momentum under different incident energy 在不同角动量下,各通过几率的稳态值变化不易看出(图2)。为了更方便观察在不同的角动量下各方法的通过几率的稳态值的变化规律,在图3中分析了各通过几率在不同条件下的稳态值。图3表示相同温度(T=4 MeV)不同入射能量(Ec.m.=7.526,16.933 5,30.104 MeV)下,通过几率随角动量的变化。上三角折线表示入射能量为30.104 MeV时的结果,圆圈折线表示入射能量为16.933 5 MeV时的结果,方块折线表示入射能量为7.526 MeV时的结果(模拟粒子数为20 000个)。可以观察到,首次通过模型的通过几率随角动量的增加基本无变化。反复多次通过模型和定义在基态位置模拟模型的结果变化趋势基本一致,通过几率随着角动量的增加而增大。这是因为随着角动量的增加,基态位置与条件鞍点之间的距离变近效应变大,使得模拟粒子更容易到达基态位置;而条件鞍点变高效应,使模拟粒子不易通过条件鞍点,这2种效应的竞争,显然距离变近效应影响更大,通过几率随角动量显著增加。同时,考虑角动量后粒子能量变高也是极有利于试验粒子通过条件鞍点的。在相同的角动量下,3种模型的通过几率都随入射能量的增加而增大。这说明入射能量显然也是影响通过几率的一个重要因素,这在文献[19]有所提及。另外,还计算了温度分别为3 MeV和4.88 MeV时的情况,得到的结果与上述结果相一致。 图4表示相同温度(T=4.88 MeV)不同角动量(L=0,6,12)下,通过几率随入射能量的变化。 上三角折线表示角动量为12的结果, 圆圈折线表示角动量为6的结果,方块折线表示角动量为0的结果(模拟粒子数为20 000个)。 分析图4,可得到与图3相似的结论:同一条件下, 角动量的变化对首次通过模型的通过几率影响很小, 而反复多次通过模型和定义在基态位置通过模型的通过几率, 会随着角动量的增加而增大。 另外,还计算了温度分别为3和4 MeV时的情况,得到的结果与上述结论一致。 图5表示角动量分别为0和6(L=0时表示没有角动量)时,不同温度(T=3, 4, 4.88 MeV)下,通过几率随入射能量的变化。实线表示角动量为6的结果,虚线表示角动量为0的结果。上三角表示温度为4.88 MeV的结果,圆圈表示温度为4 MeV结果,方块表示温度为3 MeV的结果(模拟粒子数为20 000个)。分析图5可知,显然,随着温度的提高,粒子热运动速度加快,所以无论是否考虑角动量,同一入射能量的各通过几率都随温度的升高而升高。有趣的是,首次通过模型的通过几率受温度变化的影响更大,这点与前面提到的角动量对首次通过模型的通过几率影响小不同,温度对首次通过几率的影响较其他2种方法更明显。另外还发现,温度最高的线的斜率最大,温度最低的线的斜率最小,这说明温度越高对通过几率增加的促进作用越强。 图4 不同角动量下,通过几率随入射能量的变化 图5 不同温度下,通过几率随入射能量的变化 还观察到在首次通过条件鞍点方法中,不同温度下,考虑角动量后基本没有影响通过几率随入射能量的变化结果,而在反复多次通过方法和定义在基态位置方法中,随着温度的升高,考虑角动量后的通过几率明显高于无角动量的情况,但是通过几率随入射能量升高的趋势并没有变化。在利用反复多次通过鞍点模型中,本工作希望对温度、角动量、入射能量等因素对通过几率的影响给出有意义的探讨。 在原有的熔合位垒基础上考虑了角动量的影响,利用试验粒子反复多次通过条件鞍点模型数值模拟Langevin方程来计算核熔合过程的通过几率,研究分析角动量对通过几率的影响。利用定义在鞍点的首次通过条件鞍点方法、反复多次通过条件鞍点方法以及定义在基态位置的模拟方法,研究了角动量、温度、入射能量等因素对核熔合过程通过几率的影响。研究结果表明:随着角动量的增加,基态位置右移,势阱逐渐变浅直至消失;随着角动量的增加,在基态位置与条件鞍点之间的距离变近效应、条件鞍点变高效应、总能量变大效应的相互竞争下,试验粒子的通过几率变大;在相同条件下,角动量的增加会引起反复多次通过方法和定义在基态位置模拟方法中通过几率的增大,但是对首次通过方法中的通过几率基本无影响;加入角动量以后,温度以及入射能量对通过几率的影响发生不同变化。上述研究表明考虑角动量后反复多次通过条件鞍点模型能更好地描述重核的熔合过程的物理机制。
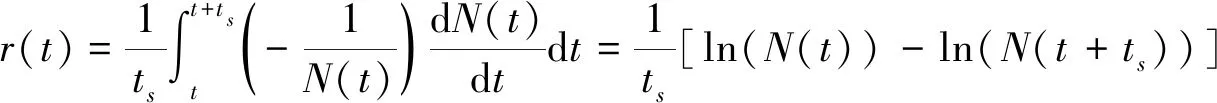

2 结果和讨论



3 总 结
