基于原位自适应制表与动态自适应机理的无焰燃烧氮转化研究

成鹏飞，李鹏飞，刘 璐，胡 帆，柳朝晖，郑楚光

(华中科技大学 煤燃烧国家重点实验室，湖北 武汉 430074)

0 引 言

天然气等气体燃料是国家能源转型期间大力发展的清洁能源，相较于其他化石燃料总体污染物生成较少，但NOx排放量亦不容忽视。我国对低氮排放的管控起步较晚但愈加严格，京津冀地区新建燃气锅炉NOx排放限值仅30 mg/m3[1]。因此，随着我国气体能源消费量的逐年增加，需要不断发展低氮燃烧技术并深入研究氮转化机理。

无焰燃烧是近年来备受关注的新型高效低氮燃烧技术，其技术关键在于反应混合物高速射流对炉内烟气的强卷吸作用，被烟气充分稀释并加热至超过自燃点的反应混合物将扩散至整个燃烧区且在局部低氧氛围下缓慢燃烧，因此整体表现为弥散燃烧状态且无明显火焰锋面[2-3]。相较于传统低氮燃烧技术，如火焰冷却技术、分级燃烧技术等[4]，无焰燃烧可从根本上抑制局部高温产生，并在保证燃烧效率、燃烧强度和燃烧稳定性的条件下实现更低的NOx排放。

计算流体力学(CFD)是燃烧研究的重要手段之一，具有简便快捷、成本低、数据丰富等优点，有效促进了无焰燃烧反应特征及NO生成调控的研究发展。无焰燃烧具有分布式低反应速率燃烧区和典型的中低温燃烧特性，需建立有限反应速率模拟以考虑强烈的湍流化学反应交互[5-7]。提高NO生成的数值预测精度是无焰燃烧数值模拟的关键[8-10]，相较于简化的半经验NOx后处理模型，基于耦合含氮详细反应机理的有限反应速率模拟可将燃烧氧化过程与氮化学反应耦合计算并考虑再循环烟气中的初始NO对着火的加速作用，从而准确预测着火和主反应区，并得到含氮中间组分分布和NO生成路径等氮转化关键信息[11]。

由于组分数、反应数较多的含氮详细反应导致实际数值计算过程耗时较长，通常需要耦合简化计算方法在不显著降低计算精度的条件下实现计算加速。原位自适应制表法(In-Situ Adaptive Tabulation, ISAT)可利用已存储的数据代替组分反应速率微分方程的复杂求解过程以减少计算耗时，在当前燃烧模拟中得到广泛应用[12-14]。动态自适应机理(Dynamic Adaptive Chemistry, DAC)可基于特定时间内每组当地瞬时热化学状态参数将详细反应机理实时简化为含最少组分和反应的精确子机理，实现计算加速。当前已有少数耦合DAC算法的气体及液体燃料燃烧模拟研究[15-19]，且笔者团队已将其拓展应用于煤粉等固体燃料[20]，但仍需进一步发展与优化该计算方法。

为提高无焰燃烧模拟的预测精度和计算速度并进一步研究分析该燃烧过程中的氮转化机理，笔者耦合含氮详细反应机理和简化计算方法进行了CH4/H2热伴流无焰燃烧模拟，发展了原位自适应制表法与动态自适应机理耦合计算方法(ISAT-DAC)并进行优化评估，最后基于经实验验证的模拟计算结果进行了氮化学反应动力学分析。

1 基于ISAT-DAC算法的数值模拟

1.1 原位自适应制表法

对于确定的反应动力学，最终反应状态是初始反应状态和时间步的函数。理论上，反应的映射关系在完成一遍计算后可制成表，当插值得出的结果满足精度要求时，可不必进行积分运算，从而节约计算时间。但由于实际尺寸过大，包含所有温度、压力、组分和时间步的预制表是不允许的，须在计算过程中制表。ISAT实质上是一种利用误差控制实时制表访问组合空间区域的加速计算方法。

在第1个时间步Δt内，若初始反应状态为φ0，则末状态为φ1可按式(1)计算：

(1)

其中，S为化学源项；t为反应时间。计算式-创建表中第1项，并包含式(2)中的映射梯度矩阵A：

(2)

(3)

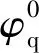
(4)

1.2 动态自适应机理简化

燃烧火焰化学成分在不同区域差别很大，因此无须在模拟计算域全局使用统一的反应动力学机理。DAC可将详细机理当地实时简化为精确子机理，以实现计算加速。

简化计算过程中首先需指定目标组分A和简化阈值λ，目标组分通常确定为燃料主要成分及燃烧过程中的关键组分，简化阈值需综合考虑计算误差和简化加速效果。通过直接关系图法[21]在每个网格单元内计算非目标组分B对目标组分A生成的贡献rAB：

(5)

其中，ωi为基元反应i的化学反应速率；vA,i为A组分在反应i中的化学计量数。当rAB>λ时将组分B保留在动态机理中。每个非目标组分对目标组分生成的贡献均需计算。

然后采用相同方法确定目标组分的间接贡献组分。若组分B包含于对目标组分直接贡献较大的组分集合中，需计算其余非目标组分K对组分B的贡献且当rBK>λ时保留K组分。对所有组分执行上述操作以确定最终保留在简化机理中的组分。

最后将所有与保留组分无关的反应去除，即得到每个网格单元的当地简化机理。通过求解简化后的低维常微分方程组，可显著缩短计算时间。因此，当λ值较大时，可减少保留组分及反应数并加速计算，但同时导致模拟误差的增大。

ISAT-DAC耦合算法，由CONTINO等[22]首次提出并应用于内燃机均质压燃(Homogeneous Charge Compression Ignition, HCCI)模拟，可充分发挥2种计算方法的优势，其计算流程如图1所示。

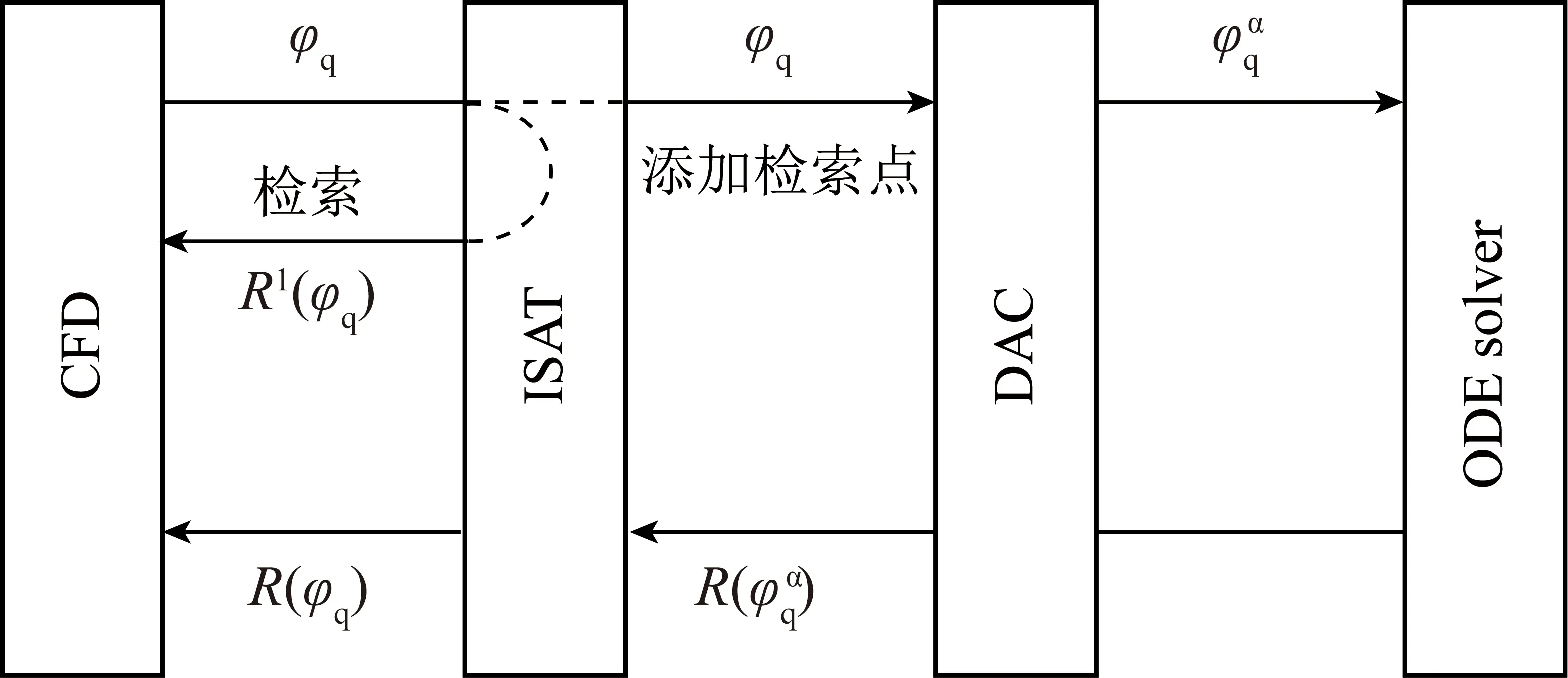
图1 ISAT-DAC计算流程Fig.1 ISAT-DAC calculation flow chart

1.3 模拟对象与计算细节

无焰燃烧模拟研究对象为同轴热伴流射流反应器[23]。燃烧器结构如图2所示，主要由中心燃料管和热氧化剂伴流管组成。以内置二次燃烧器的燃烧产物作为热氧化剂伴流，并通过控制燃烧器侧面的空气及氮气流量调节氧浓度。中心燃料管直径为4.25 mm, 热伴流流管直径为82 mm。

图2 燃烧器结构[23]Fig.2 Burner structure[23]

数值计算域如图3所示，将燃料喷口下游一段燃烧区域作为计算域，且由于全尺度含氮详细反应机理模拟需较大计算量及该燃烧器结构对称，采用轴对称二维雷诺平均模拟来简化计算三维圆管同轴射流[24-26]。计算域由喷口处轴向延伸500 mm，纵向延伸80 mm，其中纵向2.125 mm为燃料进口，燃料进口边界至纵向41 mm为热伴流进口，其余为空气风道。实验及模拟数据监测取中心射流与周围空气混合前Z=30 mm及混合后Z=120 mm截面，数据丰富且有代表性，便于进行无焰燃烧数据分析与模拟验证[23]。采用23 420单元数的网格并进行网格独立性计算，分析结果如图4所示，不同网格数量的模拟结果相近且与实验数据吻合较好，因此当前较低网格数量即可满足高精度模拟要求并加速计算。

图3 模拟计算域Fig.3 Computational domain of simulation

图4 网格无关性验证Fig.4 Grid independence validation

DALLY等[23]基于热伴流射流反应器建立了O2质量分数3%、6%和9%实验研究，结果表明热伴流O2质量分数3%条件下的燃烧状态最接近无焰燃烧。因此，笔者基于O2质量分数3%工况下的实验数据对DAC、ISAT及ISAT-DAC耦合算法的计算效果进行评估，并分析ISAT-DAC算法在无焰燃烧模拟中的适用性。具体工况参数见表1[23]。数值计算基于FLUENT求解器。采用标准k-ε湍流模型和标准壁面函数[27]，将模型系数Cε1由1.44 修正为1.60以提升圆管射流预测精度[28]。采用高精度离散坐标(DO)辐射模型求解计算域内若干离散立体角的辐射传递方程，引入灰气体加权和(WSGG)模型计算气体辐射特性参数，总发射率的空间变化是气体组分和温度的函数[29]。均相燃烧与氮转化模拟采用有限速率涡耗散概念(EDC)模型耦合GRI-Mech 3.0含氮详细反应机理(53种组分、325步反应)[30]，以描述由基元反应和中间组分控制的瞬态燃烧过程[31]。速度压力耦合方程采用SIMPLE算法以节约计算资源。空间离散采用高阶QUICK格式以提高燃烧模拟精度。

表1 工况条件[23]Table 1 Operating conditions[23]

2 模拟结果与讨论

2.1 简化算法的发展评估

基于CH4/H2热伴流无焰燃烧工况综合分析动态自适应机理简化法、原位自适应制表法及ISAT-DAC耦合简化算法的预测精度和简化加速效果，从而对无焰燃烧模拟简化算法进行发展与评估。

首先分析比较3种简化方法应用于无焰燃烧模拟研究中的预测精度。DAC、ISAT及ISAT-DAC算法的简化阈值均设置为10-4。DAC和ISAT-DAC算法的初始目标组分集合确定为CH4、HO2、CO和NO，其中CH4为燃料主要组分，CO、NO为燃烧关键组分、HO2为着火关键组分。以简化计算结果与直接积分模拟结果的相对误差作为评估标准，并按式(6)计算：

ψφ=|φID-on-φODE|/φODE，

(6)

式中，ψφ为基于3种简化方法的计算结果与直接积分模拟结果的相对误差；φID-on为基于ISAT、DAC或ISAT-DAC算法模拟得到的温度或组分浓度等燃烧关键参数值；φODE为直接积分计算结果。

一般认为，高精度燃烧模拟中主要参数或组分的预测误差限值可取5%，低含量组分的预测误差限值可取8%。选取温度及O2、H2O、CH4、CO、OH、HO2、NO体积分数计算相对误差值ψφ，结果如图5所示。可知基于3种简化方法的模拟计算结果均满足较高精度要求，且所有参数相对误差均未超过6%。不同机理简化方法对温度及O2、H2O、CH4体积分数等主要参数或组分的模拟结果影响较小，相对误差均低于1.5%，其中CH4体积分数受不同简化方法的影响较大。CO、OH、HO2、NO等低体积分数组分的模拟相对误差受不同简化方法的影响显著。基于DAC算法的所有燃烧关键参数模拟结果相对误差最低并可忽略不计，ISAT-DAC算法次之，ISAT算法的相对误差相较其他算法显著升高。

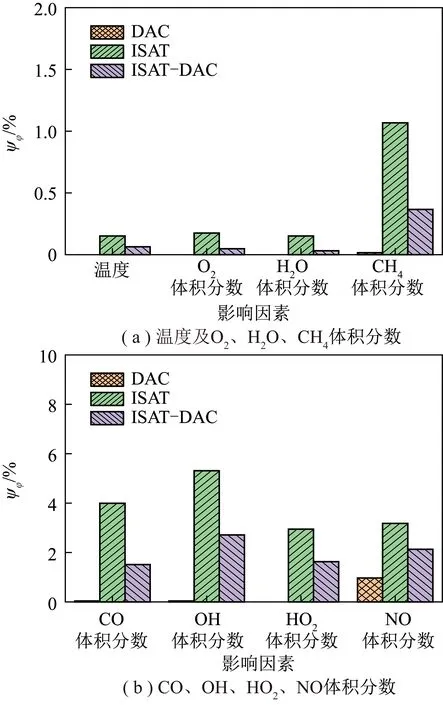
图5 3种简化方法的相对误差统计Fig.5 Relative error statistics of three simplified methods

基于DAC和ISAT-DAC简化算法的活跃组分分布如图6所示。图6(a)中单独采用DAC算法的简化计算域保留了更多活跃组分，因此数值预测精度略高，但过多的活跃组分会降低计算速度。图6(b)中采用ISAT-DAC耦合算法可将不活跃反应区域内的组分基本去除，从而精确识别反应区域，且模拟计算的相对误差亦在可接受范围。

图6 基于DAC和ISAT-DAC算法的活跃组分分布Fig.6 Active species distribution based on DAC and ISAT-DAC

分别统计基于直接数值积分法、动态自适应机理简化法、原位自适应制表法和ISAT-DAC耦合简化算法的无焰燃烧模拟计算时长，按式(7)计算加速因子并分析不同简化算法的加速计算效果：

f=tfull/treduct，

(7)

式中，f为加速因子；tfull为基于直接数值积分法模拟的计算时长；treduct为基于简化算法模拟的计算时长。

经归一化计算，直接数值积分法模拟加速因子为1。不同简化算法归一化计算结果见表2，基于DAC、ISAT及ISAT-DAC算法的模拟加速因子分别为1.3、1.8和3.2，因此不同简化算法均可减少计算时长。对于耦合GRI-Mech 3.0机理的气体无焰燃烧模拟，采用ISAT算法相较于DAC算法可获得更快的计算加速，且ISAT-DAC耦合算法可在DAC或ISAT算法基础上大幅提高计算速度。

表2 3种简化方法的加速因子Table 2 Acceleration factors of three simplified methods

2.2 动态自适应机理最优简化阈值

据第2.1节不同简化算法的评估分析可知，DAC算法可在一定程度上实现无焰燃烧计算加速且精度最高，进一步结合ISAT算法的计算优势可在保证较高精度的条件下大幅提升计算速度。基于ISAT计算加速的方式已在燃烧模拟中得到广泛应用，本节旨在寻找ISAT-DAC耦合算法的最佳DAC简化阈值。

反应机理仍选用GRI-Mech 3.0[30]。ISAT阈值设定为10-4，DAC简化阈值分别选取10-4、10-3、10-2和10-1，并按式(6)分别计算基于不同简化阈值的相对误差。温度及O2、H2O、CH4、CO、OH、HO2、NO体积分数的模拟相对误差如图7所示。

图7 ISAT-DAC算法中不同DAC阈值相对误差统计Fig.7 Relative error statistics of different DAC thresholds in ISAT-DAC

由图7(a)可知，温度及O2、H2O、CH4体积分数模拟结果受不同DAC简化阈值影响较小，相对误差均不超过4%。DAC简化阈值10-2条件下的模拟相对误差仍较小，进一步增大至10-1时相对误差显著升高。图7(b)中CO、NO、HO2、OH体积分数对不同DAC简化阈值更加敏感，且DAC简化阈值10-2条件下的低含量组分模拟相对误差未超过8%。DAC简化阈值10-1条件下的NO和HO2体积分数的模拟相对误差超过10%，且CO和OH体积分数的模拟相对误差亦趋近10%。综上，DAC简化阈值10-2条件下仍可保证较高的模拟精度。

基于ISAT-DAC耦合算法和不同DAC简化阈值的活跃组分分布如图8所示。随着DAC简化阈值的增大，ISAT-DAC耦合算法的计算简化能力增强。DAC简化阈值10-4时整体反应区域基本包含GRI-Mech 3.0详细机理的所有组分，DAC简化阈值10-3时整体反应区域组分数略有减少，但大部分区域保留了较多组分。当DAC简化阈值增至10-2时，反应区域中保留的活跃组分数进一步减至约30种。简化阈值10-1时的反应区域活跃组分数目仅余20种左右，因此CO、NO、HO2、OH等体积分数较低的组分在此阈值条件下的模拟相对误差较大。

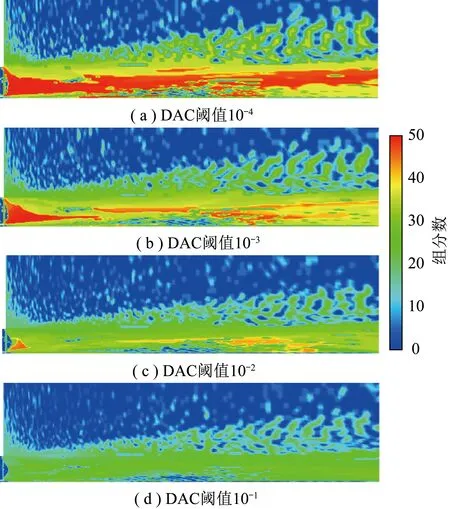
图8 ISAT-DAC算法中不同DAC阈值活跃组分分布Fig.8 Active species distribution of different DAC thresholds in ISAT-DAC

统计基于ISAT-DAC算法和不同DAC简化阈值的模拟计算时长，归一化计算后加速因子见表3。DAC简化阈值10-2条件下的模拟计算中，计算速度相较于10-4时显著提升。继续增大简化阈值对加速因子影响较小，而燃烧关键参数，尤其是CO、NO、HO2、OH体积分数的模拟精度显著降低。因此，综合相对误差与简化加速效果，ISAT-DAC耦合算法中DAC最佳简化阈值为10-2。

表3 ISAT-DAC算法中不同DAC阈值加速因子Table 3 Acceleration factors of different DAC thresholds in ISAT-DAC

2.3 不同复杂度机理的简化效果

当前数值计算中一般无须选用高复杂度详细机理即可满足所需精度要求，但基于不同组分数和反应数的详细机理可对ISAT-DAC耦合算法在无焰燃烧模拟中的适用性和优越性进行更加全面的评估。采用3种详细机理，机理中所包含的组分数和反应数由低到高分别为DRM22机理(22种组分、83步反应)、GRI-Mech 3.0机理(53种组分、325步反应)[27]及PG2018机理(151种组分，1 397步反应)[32]。3种详细反应机理经ISAT-DAC算法简化后的活跃组分分布如图9所示，由于无焰燃烧过程中存在复杂的湍流化学相互作用，3种不同详细机理模拟的燃烧反应区域均保留了大多数组分和反应。由于DRM22机理的组分数和反应数较少，简化空间较小，燃烧反应区域几乎保留了该机理中的全部组分，非反应区域的组分数基本为0以节省计算耗时。GRI-Mech 3.0机理和PG2018机理的组分数及反应数较多，ISAT-DAC算法简化效果显著。基于GRI-Mech 3.0机理的燃烧反应区域中约保留原机理中75%的组分，且反应区域上游的活跃组分数进一步减至20种左右。PG2018机理简化空间最大，燃烧反应区域中消除了原机理中约50%的组分。

图9 基于ISAT-DAC算法的不同复杂度机理活跃组分分布Fig.9 Active species distribution of different complexity mechanisms based on ISAT-DAC

分别统计基于3种不同复杂度的详细反应机理和不同简化算法的模拟计算时长并按式(6)计算加速因子，结果见表4。随着机理复杂度的提高，模拟简化空间增大，基于不同简化算法计算的加速因子均增大。耦合DRM22机理或GRI-Mech 3.0机理时的DAC简化加速因子略低于ISAT算法，而耦合PG2018机理时的结果相反，因此DAC算法所实现的简化加速效果相较ISAT算法对反应机理的复杂程度更加敏感，即DAC算法对高复杂度反应机理表现出更加优异的简化计算潜力。不同简化算法对于耦合低复杂度DRM22骨架反应机理模拟的加速因子较小，基于ISAT-DAC算法模拟得到的加速因子仅为1.7，基于DAC算法模拟的简化加速效果可忽略不计。相较于DRM22机理，不同简化算法对于耦合GRI-Mech 3.0详细机理模拟的加速因子略有增大，且ISAT-DAC耦合算法的简化加速效果较为可观。相较于DRM22机理或GRI-Mech 3.0机理，对于耦合多组分、多反应的PG2018大型详细反应机理模拟，基于不同简化算法的加速效果显著增加，ISAT-DAC耦合算法所对应的加速因子高达10.8，从而大幅缩减计算时长。

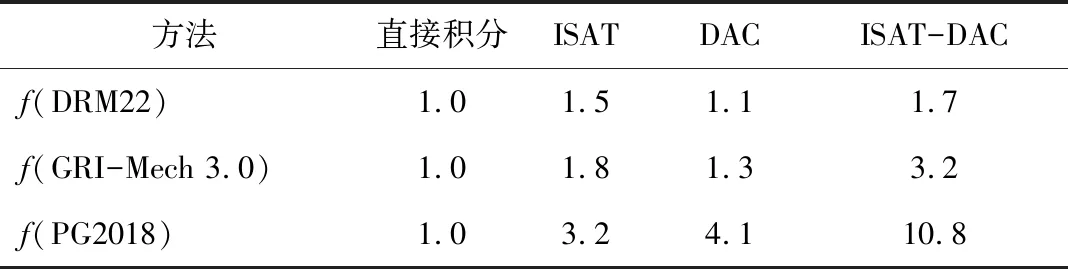
表4 不同复杂度机理的简化加速因子Table 4 Acceleration factors of different complexity mechanisms

2.4 实验验证与氮转化路径分析

将基于GRI-Mech 3.0机理及ISAT-DAC耦合算法且DAC简化阈值10-2条件下的数值计算结果与O2质量分数(y(O2))3%工况下的CH4/H2热伴流无焰燃烧实验数据进行对比分析以验证所选简化算法及误差阈值的准确性。

轴向30、120 mm截面处分析计算结果如图10所示(x表示物质的体积分数)，测量不同截面的温度及O2、H2O、OH、CO的质量分数及NO体积分数，相应模拟计算结果与实验数据基本吻合，可较准确预测上述燃烧关键参数，包括广为关注的低浓度CO和NO组分。

图10 模拟与实验的数据验证Fig.10 Data validation between simulations and experiments

NNH中间体由H与N2在火焰条件下快速生成，并进一步结合O原子生成NO：

(8)

(9)

N2O中间体由O与N2及火焰中的其他组分M通过复合反应生成：

(10)

部分N2O中间体通过下列反应被重新还原为N2：

(11)

(12)

(13)

其余N2O中间体进一步结合O原子生成NO：

(14)

当前燃烧模拟研究大多基于ISAT算法实现详细机理模拟的计算加速，因此本文对比分析了采用ISAT算法模拟时的氮转化路径，如图11(b)所示。基于单独ISAT算法模拟时的氮转化路径和反应速率与ISAT-DAC简化算法有所差别，但主要反应路径基本一致。大多数反应路径的反应速率在同一数量级，少数反应速率相差一个数量级。由于DAC算法对含氮反应路径的简化作用，基于ISAT-DAC耦合算法的模拟反应路径相较ISAT算法更加精简。

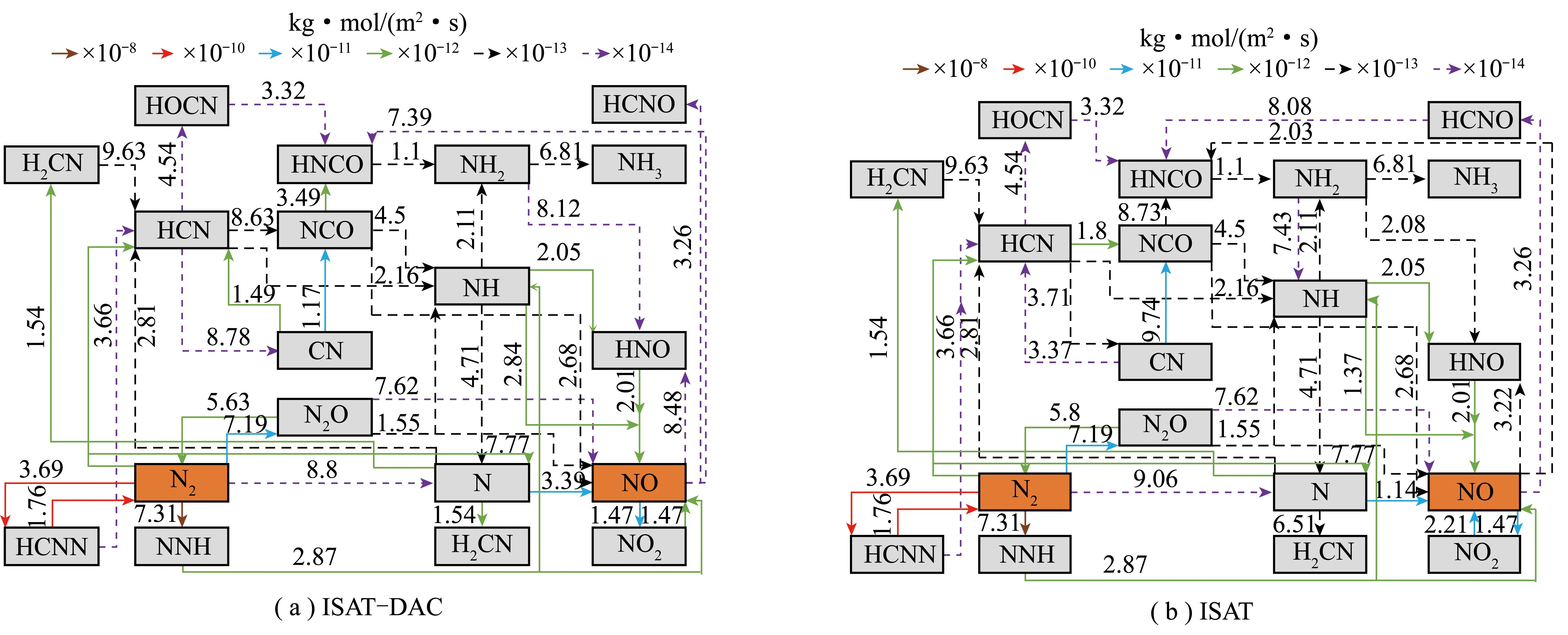
图11 CH4/H2热伴流无焰燃烧氮氧化物转化路径Fig.11 NOx conversion path of CH4/H2 flameless combustion with a hot co-flow

3 结 论

1)不同简化计算方法对CO、OH、HO2、NO等低浓度组分的模拟相对误差影响显著。采用单一DAC算法精度最高，但计算加速效果并不明显；ISAT算法精度最低，而计算速度相较于DAC算法提升较小；ISAT-DAC算法可保证模拟所需的较高精度并大幅实现计算加速，是综合预测精度与简化加速效果的最优算法。

2)基于ISAT-DAC耦合算法且DAC简化阈值设定为10-2的模拟计算中，相较于DAC简化阈值10-4条件下可保留主要燃烧组分及反应，并在保证较高模拟精度的条件下实现显著计算加速。当简化阈值增至10-1，燃烧关键参数的模拟相对误差显著升高，而计算速度提升较小。因此DAC简化阈值10-2时综合效果最优。

3)多组分、多反应的复杂机理具有更高的简化计算空间。基于ISAT-DAC算法和PG2018大型含氮详细机理模拟的燃烧反应区域仅保留约50%的原机理组分，可在保证所需模拟精度的条件下实现约10.8倍的计算加速。DAC算法相较于ISAT算法对高复杂度机理表现出更优异的简化计算潜力。

4)基于实验验证与氮转化路径分析，CH4/H2热伴流无焰燃烧NO生成主要取决于NNH路径和N2O中间体路径，热力型NO及快速型NO可忽略不计。相较于ISAT算法，基于ISAT-DAC耦合算法的氮转化路径可保留主要NO反应并适当精简。