基于Hamel形式的柔性集群编队围捕*
2022-08-25张祺黄彬史东华
张祺 黄彬 史东华
(北京理工大学数学与统计学院,北京 100081)
引言
在过去二十年中,集群控制逐渐成为诸多领域研究热点.与传统的集中式控制系统相比,集群控制系统具有灵活的可扩展性、对个体数量的变化适应性强、运行成本低而不增加整个系统的复杂性等优点.简单个体之间的协同合作可以提升群体的智能化程度,而得以胜任很多单个体无法完成的工作,往往能带来更加优秀的表现[1].因此,集群系统不仅在理论层面得到了控制学界的关注,而且在特定的场景与任务下得到了广泛的应用.例如在军事领域,为克服个体作战能力的不足,需要用大量个体通过编队协作,实现复杂的军事任务.其应用包括无人机群战场侦察[2]、无人作战集群 (UUVs,AUVs)围捕目标[3,4]等.在航天领域,通过航天器集群协同去降低任务成本,涌现了卫星编队任务系统[5,6]、航天器集群深空探测[7]等相关研究.
集群系统的应用需要实现集群的编队控制,即稳定和保持集群的几何队形,通过形成预期的队形模式完成任务.合理、高效的编队控制能提高集群系统的性能,如对目标搜索的效率,对目标围捕的成功率和对随机环境干扰的鲁棒性等[8].
近年来,集群系统的研究对象逐渐由一阶或高阶线性系统,过渡为更具有一般性的高维或无穷维非线性系统,对其已提出多种新颖的控制框架以达成更好的效果.例如,为实现大规模集群有限时间的布放编队控制,Meurer等[9]构造一类非线性时变偏微分方程,通过改变边界条件和方程参数,使得解曲线在二维平面内运动,利用边界控制实现集群编队的运动规划和队形变换.该方法中方程的空间离散节点对应集群系统的个体,空间离散方式对应集群通信的互联结构,可以适用于大规模集群.其编队的稳定性直接由偏微分方程性质保证,但控制律的计算涉及复杂的级数表达式,应用中其实时性难以保证.另一种备受关注的编队控制方法是利用连续介质力学对集群系统建立模型[10],通过将集群中的个体视为连续体中的质点粒子,将集群的运动过程视为连续体的演化过程(含平移和形变),可以从原理上避免集群内个体间的碰撞,通过控制该连续体的运动实现集群编队控制,同时能有效处理相应的队形变换问题.这是虚拟结构方法的推广,可以很大程度上避免其不够灵活、刚性过强的弊端.但这一方法同样具有计算量大、需要选取主个体等缺点,依然有进一步完善的空间.Rastgoftar等[11]通过在主-从编队控制框架下使用齐性映射,克服了之前连续体控制模型对通信要求过高的困难,使得无论在固定通信拓扑还是切换通信拓扑下,集群都能获得齐性映射所规定的期望位置.
同样,作为工程中应用极其广泛的典型系统,Euler-Lagrange系统的集群控制也受到学界的关注.尤其是处理无人机编队、近地卫星集群等系统时,系统中个体的动力学特性不能简单忽略,只考虑线性系统建模是不够的.为此,Nair等[12]考虑了较为简单的沿空间一维曲线分布刚体集群编队,通过能量塑形为个体构造势能塑形后的Lagrange函数实现了刚体集群编队,并通过航天器集群协调旋转实验表明所得控制可以实现编队同步化.
未来针对集群的研究将更加面向具备非线性动力学特征的实际集群场景和大规模集群编队.虽然集群编队控制已有较为丰富的控制工具,但一方面大多数方法将个体视为质点,只考虑了其位置信息或相对位移,在无人机编队、潜航器编队等关注姿态的应用场合,这类方法建立的模型有局限性;另一方面,针对数量规模较大的集群,虚拟结构方法和基于连续体模型的编队方法面临计算复杂度高、难以在线计算等挑战.为解决这些问题,我们建立了基于场论的Hamel形式的柔性编队控制框架.场论Hamel形式[13]是将活动标架融入变分原理,得到的一种描述场论中运动的标准型;柔性编队是将个体嵌入一个虚拟弹性体,使得集群中个体自然避撞、运动平滑并保持姿态的一致性,尤其适用于大规模集群.本文在场论Hamel形式框架基础上,研究利用柔性编队实施围捕的算法.其余部分安排如下:首先,建立将集群编队嵌入几何精确梁的算法模型;其次,用编队平衡对流应变建立虚拟的编队弹性势能,通过势能塑形控制,实现编队队形的弹性变换,藉此建立柔性集群编队围捕的控制算法;最后,通过模拟仿真验证围捕算法的有效性,满足相应类型任务需求.
1 集群系统的Hamel形式
考虑沿空间一维曲线均匀分布的集群,同样的方法也适用于其在空间更高维几何体均匀分布的情形.我们将集群个体嵌入到几何精确梁中(见图1),得到一类Hamel形式的集群编队动力学方程,并构造编队平衡态势能来控制编队形式.
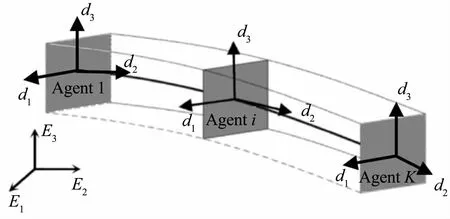
图1 集群嵌入几何精确梁Fig.1 Swarm embedded in a geometrically exact beam
1.1 Hamel形式集群系统动力学方程
选择几何精确梁作为嵌入的弹性体对象原因在于:一方面通过其刚体截面描述集群中的个体位置与姿态,另一方面用其弹性变形的性质可以描述并实现集群编队的大范围运动、队形变换和避撞等.关于几何精确梁的建模和相关保结构算法详见文献[14].长度为L的几何精确梁的位形可由映射g:[0,L]×R→SE(3)表示,其时空自变量分别是s和t.设集群个体i为位于梁沿中线si处的截面,0≤si≤L,其位姿gi=g(si,·):[0,T] →SE(3)表为


1.2 集群系统的Hamel形式离散格式


和实际的初值条件.
注意到利用离散变分原理得到的Hamel场积分子(6)联合离散相容性条件(7)恰好形成交错蛙跳格式,由文献[15]可知此格式中涉及集群中个体运动的计算只和相邻的个体有关,故可用分布式的并行计算实现,从而满足实时控制的计算需求.
2 集群系统的编队控制
为实现对目标的围捕,从任务需求来看集群控制需具备两种基本功能:1)控制编队保持特定队形;2)实现特定队形变换.这可通过对集群系统Hamel场方程(6)中的外力 τni分别采取轨迹跟踪、编队保持控制来实现,以及通过编队势能的塑形来实现编队变换和围捕过程,具体实施过程如下:首先,对群中领导者应用轨迹跟踪控制;其次,对跟随者实施编队保持控制,引导整个集群协作去追击围捕目标;最后,在迫近围捕目标时,通过编队势能的塑形控制进行队形变换来完成围捕.
2.1 集群的控制

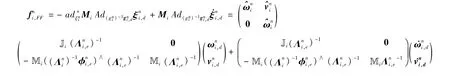
其中, skew(A) =(A-AT),Kp1,Kp2,Kd1是三阶自伴(对称)矩阵,Kd1为三阶正定矩阵,∨为帽子映射∧的逆映射,定义与之类似.Bullo等[16]证明了上述控制律可以使被控刚体的状态收敛于目标状态.
为实现集群队形保持,借鉴几何精确梁的弹性势能使梁在适当变形后自动恢复至平衡位置的原理,根据集群系统的离散Hamel方程(6)式,可以给出集群中个体i所需集群编队控制力
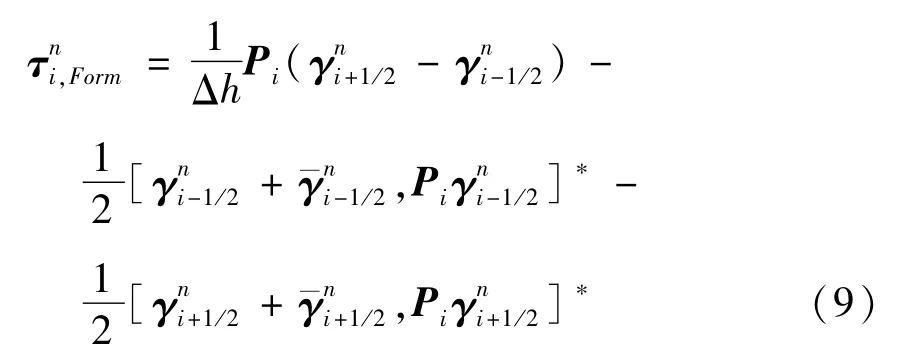
2.2 虚拟弹性势能塑形实现队形变换
通过改变集群系统的Hamel形式(6)和相容条件(7)中的对流应变,来达到塑形弹性势能并实施编队变换.假定所有的集群个体位姿都在编队稳定平衡状态,由离散平衡对流应变定义式(5)可知,存在映射log:,这里映射log为指数映射exp的逆映射.注意到指数映射仅是局部微分同胚,映射log在单位矩阵的邻域内定义,也即当集群中相邻个体位姿相差较小时成立.反之,已知初值和结合(4)式可重构,将此映射记为R.对编队势能集合进行塑形可控制集群编队变换.令编队初始状态编队平衡位姿为,末态编队平衡位姿为,与其相关的编队平衡对流应变分别是,则有如下交换图成立

由上图可知:只要定义由编队变换函数F诱导出的函数f,改变位于李代数空间(线性空间)中编队平衡对流应变,就可以改变位于李群空间 (非线性空间)中的位形,实现对编队势能的塑形,进而来控制编队队形.在物理上,此过程可解释为通过施加一种场控制来实现集群的编队变换.为简单起见,此处仅考虑一类在对流应变空间se(3)中的线性插值函数R6… ×R6,使得

通过该线性插值过程实现编队势能塑性.
2.3 集群系统编队与围捕算法
为了实现集群围捕任务需求,本文仅考虑对固定目标的围捕,主要通过对编队势能的塑形控制来实现编队变换,建立如下集群围捕控制算法实现集群编队巡航、编队围捕.

图2 控制算法流程图Fig.2 Flow chart of control algorithm
3 集群编队与围捕控制仿真
为了验证集群围捕控制算法的有效性,本节针对固定目标进行围捕过程的模拟仿真.仿真中集群将先保持队形进行编队巡航,后用“半圆”和“V”型两种模式对目标展开围捕.
3.1 “半圆”型围捕模式
考虑围捕目标位置为 A=(6,2.4,0)T,集群初始位置如图3(a)所示,其参数如下:个体总数K=9,编号5的个体为领导者,初始编队长度L=π,惯性矩阵 Mi=dig(10,10,10,10,10,10) , 伪弹性系数阵 Pi=dig(1,1,1,0.6,0.6,0.6) ,除了另加声明,本文后续中 i=1,2,…,K.

图3 集群编队围捕初始状态示意图Fig.3 Schematic diagram of initial states of swarm



利用上述初始值作为集群围捕控制算法的输入,用Matlab编程进行仿真知:平均计算控制响应时间为1.6ms,远小于时间步长Δt=0.1s.这表明该算法可以用来在线计算,并实时地控制编队运动过程.仿真过程可见图 4,其中,图4(a),图4(b)和图 4(c)显示集群呈一字型编队巡航,图 4(d),图4(e)和图4(f)显示其以半圆型模式围捕目标物.图5展示了集群在围捕过程中每个个体所受到的控制力和力矩,及自身动力学状态随时间的变化情况.

图4 集群编队“半圆”型围捕的模拟仿真Fig.4 Simulation of target-capturing in “Semicircle” shape

图5 集群编队围捕实时控制和速度Fig.5 Real-time controls and velocities of the swarm
3.2 “V”型围捕模式
此例表明所得算法同样适用于非光滑队形变换.固定围捕目标位置为 A=(6,2.4,0)T,集群初始位置如图3(b)所示,其参数如下:编队个数K=11,编号6的个体为领导者,初始编队长度L、惯性矩阵Mi和伪弹性系数矩阵Pi与“半圆”型围捕一致.


对上述初值仿真结果可见图6,其中,图6(a),图5(b)和图6(c)显示该集群中的11个个体保持一字型编队巡航,图 6(d),图 6(e)和图 6(f)显示集群以“V”型模式围捕目标物.图7展示集群在围捕过程中每个个体所受到的控制力和力矩,及相应的自身动力学状态.此时每个时间步迭代用时为2.0 ms,计算时长小于时间步长,因此满足实时控制的基本需求.

图6 集群编队“V”型围捕的模拟仿真Fig.6 Simulation of target-capturing in“V” shape

图7 集群编队围捕实时控制和速度Fig.7 Real-time controls and velocities of the swarm
从上述两个例子的仿真结果可知:通过改变平衡对流应变ˉγni+1/2可以控制集群编队形成不同的队形,并且这种通过对虚拟弹性势能塑形所实现的队形变换过程自然,只需要在李代数空间线性插值,在编队变换过程中,个体间的虚拟势能可以避免个体间发生碰撞,并能满足实时控制需求.并且本算法可结合各种围捕策略,通过改变ˉγni+1/2来实现不同的围捕队形.
4 结论
本文针对集群系统,提出了一种柔性编队围捕算法.通过离散变分原理,给出了基于几何精确梁Hamel场变分积分子的算法实现.与传统方法相比,基于动力学的模型可以综合考虑个体的位置和姿态;由离散变分得到的数值格式结合离散相容性条件,可以分布式计算每个个体的运动状态,其计算速度可满足实时控制需求.特别地,本文构造了编队平衡对流应变,以此实现对编队虚拟弹性势能的塑形,来控制编队队形的弹性变换.通过模拟对固定目标的“半圆”型和“V”型围捕,仿真结果验证了该算法在实际场景中的适应性和有效性.未来的研究将致力于实现不同编队拓扑结构下的控制算法,及对算法收敛性、控制稳定性的理论分析;以及实现对三维空间中目标的围捕、多个活动目标的围捕和带有博弈过程的围捕等.
