基于变步长LMS方法的磁悬浮飞轮振动抑制*

王雨楠 刘昆

（中山大学航空航天学院，广州 510275）

引言

磁悬浮轴承相比传统轴承有许多优点，如不存在机械接触、无磨损、低功耗，在极端温度和较高速度下运行能力较好[1].因此电磁轴承已经广泛应用于高速透平机械等工业领域以及磁悬浮飞轮等航天领域.电磁轴承有两个主要的振动源，转子质量不平衡和传感器噪声.质量不平衡是由于实际制造的材料与加工工艺限制，主轴的惯性轴与几何轴线不重合，转子高速旋转时会产生不平衡振动[2].传感器扰动是由于传感器表面不均匀及其他非线性因素，导致在传感器测量环节引入干扰，传感器扰动主要导致谐波干扰.

对于电磁轴承的振动抑制主要有两种：一种为不平衡补偿，以“零转子位移”为目的.另一种为自动平衡，实现力或电流的最小补偿[3].国内外学者对此作了许多研究，Herzog等[4]提出一种具有自由极点位置的广义陷波滤波器，可以处理不同转速下的同频不平衡信号，但是不能补偿位移刚度力引起的振动.Shi等[5]提出一种基于LMS自适应滤波算法的自适应前馈法，实现转子最小位移补偿.Liu等[6]提出一种开环轴承力补偿方法来抑制不平衡振动，采用自适应陷波器识别位置信号中的同频位移，但是并没有考虑功率放大器的低通特性.这些方法主要针对同频振动，针对传感器谐波噪声引起的扰动问题，Setiawan等[7]提出了一种自适应的传感器扰动补偿算法.它保证了转子几何中心的渐近稳定，并利用持续激励在线前馈消除扰动.Xu等[8]提出了一种基于重复控制器的谐波振动力消除方法，实验结果表明该方法能有效地消除谐波电流.Cui等[9]提出利用改进的重复控制器抑制主被动磁悬浮控制力矩陀螺中的谐波电流，试验证明了该方法具有较好的抑制性能.张激扬等[10]基于一种级联相移陷波器对磁悬浮飞轮全转速范围内的传感器谐波扰动进行了主动抑制.Zhou等[11]提出针对奇次谐波的改进重复控制器，消除PWM逆变器跟踪误差.

本文对磁轴承-转子系统的位移刚度系数kh和电流刚度系数ki进行辨识，提出利用自适应LMS算法实现对传感器扰动引起的八倍频振动进行抑制，在此基础上改进一种随转子位移信号频率变化而变化的变步长因子实现自动平衡，利用广义根轨迹分析插入自适应LMS算法后系统的稳定性，并通过仿真分析验证了该方法的振动抑制效果.

1 磁悬浮轴承系统建模

1.1 磁轴承-转子系统动力学建模

磁轴承-转子系统考虑细长转子，转子两端分别安装一个径向磁轴承，分别产生沿转子径向的电磁控制力.图1是转子受电磁力作用的示意图.

图1 转子受力分析Fig.1 Free-body diagram of the rotor

由牛顿第二定律和动量矩定理可得到转子动力学方程：

式中，FAX、FBX为转子沿 x方向的电磁力，FAY、FBY为转子沿y方向的电磁力，α、β分别为转子绕x、y轴旋转的角位移，Ω为转速，l为转子长度，m为转子质量.对磁轴承的磁力线性化可得：

式中，ki为电流刚度系数，kh为位移刚度系数.

1.2 振动源建模

磁悬浮飞轮悬浮控制系统中存在多个干扰源，不平衡干扰力是在转子动力学环节引入的振动干扰.受到加工工艺和安装误差等因素影响，传感器测量环节和磁力产生环节也会引入干扰.传感器各环节引入的噪声可以等效为测量面的不规则，可以称之为传感器扰动（Sensor Runout），如图2所示.

图2 传感器扰动示意图Fig.2 Sensor runout diagram

在转子旋转时测量面的不规则会给悬浮控制系统引入周期干扰，这些干扰可以用转子同频和倍频的傅里叶级数建模.传感器扰动在传感器坐标下表示为[12]：

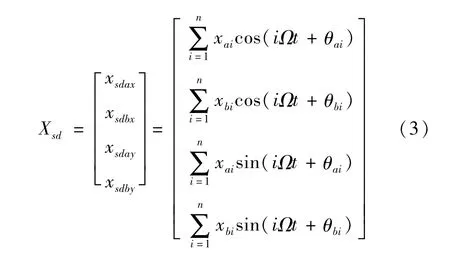
式中，i为谐波次数，i=1，2，… n ； xai、xbi为磁轴承A、B两端传感器输出信号的第i次谐波的幅值，θbi分别为相应的初始相位.本文主要考虑传感器扰动的八次谐波.

1.3 参数辨识

对位移刚度系数khx和电流刚度系数kix进行辨识.当转子水平放置在试验台上时，动力学方程为：

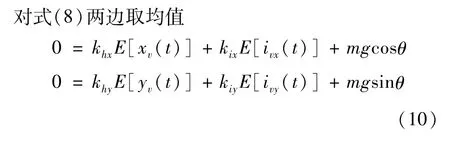
图3 垂直悬浮时转子受力示意图Fig.3 Force diagram of the rotor in vertical suspension

由于存在控制作用，偏置位移产生的位移刚度力与水平放置时相同，而控制电流中额外包含了克服重力而多出的部分.由式（10）减去式（6）得：受PID控制器中积分项作用，给定位移偏置指令后，最终稳态的位移偏差为0.令给定的偏置位移指令相等，有：

测量得到 E[ivx（t）] 、E[ihx（t）] 、m和 θ，可以计算得到kix.为了提高精度，可以多点测量求均值，根据式（7）和式（13）可以得到khx.

2 基于自适应LMS的主动振动控制

2.1 标准LMS算法

图4给出了加入LMS自适应算法的磁轴承-转子系统悬浮控制结构框图.可以看出LMS滤波器加在了悬浮控制器之前的位置.图5则给出了LMS算法结构图.

图4 加入LMS自适应算法的磁轴承结构图Fig.4 Structure diagram of magnetic bearing based on LMS adaptive feedforward

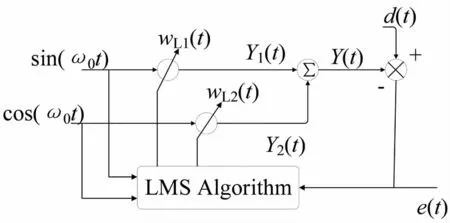
图5 LMS算法结构图Fig.5 Structure of LMS algorithm

定义 X（t） =[sin（ω0t） cos（ω0t）]T为输入信号向量，W（t） =[wL1（t） wL2（t）]T为权向量，d（t）为需要滤除的信号，Y（t） 为算法输入信号，e（t） 为误差信号，ω0为滤波角频率，μ为步长.由图5可以得到LMS算法的时域方程为：

该函数零点为 z0=e±jω0，当 d（t） 的频率 f等于算法输入信号频率f0时，有H（z）=0，可以实现对d（t） 的滤波.

2.2 变步长LMS算法

固定步长LMS算法只能对某些固定转动频率具有好的补偿效果，对于不同的旋转频率，需要选择合适的步长因子，才能有效地滤除振动干扰.文献[14]分析了几种变步长LMS算法的滤波效果，提出一种变步长改进算法，步长因子为

式中，fr为实时监测到的转子转动频率，μ1为一个很小的正参数，γ为加权系数，一般在20-30之间.但是式子中有两个调节参数，对于高速旋转的转子，需要调节的参数越多，在试验中的不利因素越多，因此文献[15]在此基础上提出改进的变步长LMS算法，步长因子为：

μ′1是一个很小的值，只有一个需要调节的参数.

3 仿真分析

搭建SIMULINK模型对上述算法进行仿真.表1给出了仿真中用到的系统参数.

表1 模型参数Table 1 Parameter of the model

采用PID控制器，其传递函数的具体形式为：

式中，kP是比例系数，kI是积分系数，kD是微分系数，N表示微分器的深度.功放模型简化为一阶惯性环节，即：

式中，kw为功放增益，τ为功放时间常数.

转子系统传递函数为：

式中，m为转子质量，ki为电流刚度系数，kh为位移刚度系数.位移传感器用比例增益表示：

绘出加入基于LMS陷波器的磁悬浮轴承系统转速根轨迹的主导零极点如图6所示，从图中可知系统在低转速时存在不稳定极点.可以考虑在低频时不加补偿，转速达到一定值后再加入补偿.

图6 根轨迹图Fig.6 Diagram of root locus

考虑正弦信号xsd=A cos（8Ωt+θ） .可以看出，该信号的频率是转速的8倍，将其作为传感器扰动，加入系统后进行仿真.在仿真开始前3s内，不启动LMS算法，3s时启动LMS算法，仿真结果如图7和图8所示，仿真中的转速Ω=2000rpm.

图7 电流收敛过程时间关系曲线Fig.7 The simulation results of the coil currents

图8 位移收敛过程时间关系曲线Fig.8 The simulation results of the displacement signal

从仿真结果可以看出，对于传感器扰动引起的八倍频扰动，加入LMS反馈补偿后，转子的位移和电流都迅速收敛到极低值地扰动进行了抑制.

4 结论

本文对磁悬浮转子存在传感器谐波噪声情况下的振动控制问题进行了研究，通过引入自适应LMS反馈补偿，减小了电流和位移信号中的八倍频扰动，提出了一种改进型的随转速变化的变步长因子，能够实时对变转速的转子实现振动抑制，通过仿真研究验证了该方法具有较好的抑制效果.但是本文只针对八倍频扰动进行了研究，对于其他倍频扰动的同步抑制还有待研究.