智能网联异质交通流混合特性

吴德华 ，彭 锐 ，林熙玲

（福州大学土木工程学院，福建 福州 350108）

随着汽车产业与人工智能、物联网、云计算等新一代信息技术深度融合发展，智能网联车辆（connected and autonomous vehicle，CAV）应运而生.CAV有自适应巡航控制（adaptive cruise control，ACC）及协同自适应巡航控制（cooperative adaptive cruise control，CACC）两种跟驰状态.ACC应用车载检测设备获取前车加速度、速度等信息，并实现本车的加速度优化.CACC立足于ACC，利用车车通信获取前车行驶信息.相比ACC系统，CACC更加精确，但CACC功能的实现需要前车安装车车通信设备.因此，当CAV跟随人工驾驶车辆（human-driving vehicle，HV）时，由于HV缺乏车车通信设备，CAV将由CACC状态自动退化为ACC状态，同时仍保留车车通信系统，与紧随其后的CAV车辆实现车车通信，并以CACC协同队列状态行驶[1].

CAV车辆的普及是一个长期的过程，CACC技术的发展会促使人工驾驶车辆逐步安装车车通信设备.于是道路交通流将会历经ACC与HV混合（前期），ACC、CACC与 HV混合（中期）和 CACC与HV混合（后期）三个阶段，这种CAV与HV混合交通流被称为异质交通流（简称异质流）.异质流的混合特性体现了CAV对传统交通流改善规律，具有前瞻性的理论研究价值及实际研究意义.

国内外学者对于异质流的研究已取得一定成果，主要涉及CAV车辆对通行能力的提升、对交通安全的影响以及对交通流稳定性的改善.Ntousakis等[2]针对ACC车辆研究了无匝道基本路段以及环形道路的交通流通行能力；Talebpour等[3]通过数值仿真实验，给出了不同CAV渗透率下混合交通流流量关于密度的散点图；秦严严等[4]对异质交通流进行了稳定性解析，并构建了基本图模型；常鑫等[5-6]推导出CAV车辆形成协同队列时的基本图，并对高速公路的通行能力进行分析；马丽娜[7]提出了基于安全距离的元胞自动机交通流模型.

综上所述，目前对于异质流的研究都涉及到CAV的渗透率分析，但仅作为随机参数，缺乏进一步的探讨.本文将探究高速路环境下，CAV渗透率对异质流通行能力提升的深层原因，并引入相对熵（Kullback-Leibler，KL散度）定量描述异质流的有序性.

1 异质流仿真基本图

1.1 异质流车辆跟驰模型

选取应用广泛的智能驾驶员模型（intelligent driver model，IDM）作为 HV、ACC车辆跟驰模型，美国加州PATH实验室车辆跟驰模型为实车测试数据标定的CACC模型[8].

Treiber等[9]提出的智能驾驶模型包含自由状态下的加速趋势和考虑与前车碰撞的减速趋势，如式（1）所示.

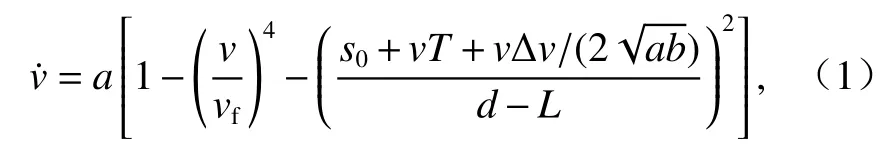
式中：v为车辆当前速度；a为车辆最大加速度；vf为最大速度；s0为最小安全间距；T为安全车头时距；b为期望减速度； Δv为车辆与前车的速度差；d为车头间距；L为车长.

各参数取值如表1所示[4]，其中：ACC车辆较HV车辆有更短的反应时间及跟车时距，故ACC车辆的T取1.1 s，HV车辆的T取1.6 s.

表1 IDM参数取值Tab.1 Values of IDM parameters

CACC 跟驰模型[8]如式（2）所示.

式中：vprev为上一时刻车辆速度；e为实际车间距与期望车间距的误差；CACC车辆的T取0.6 s；kp、kd为控制系数，根据实车标定结果，kp=0.45 ，kd=0.25.

1.2 基于CAV特性改进的NaSch模型

元胞自动机模型是于20世纪50年代提出，并于80年代末首次应用于交通流的微观仿真[10]，最具代表性的元胞自动机模型是由Nagel和Schrekenberg于1992年提出的NaSch模型[11]，该模型可以描述一些实际交通现象，但并行更新过程中无法考虑前车运动对后车车前空间的影响，导致所模拟的最大交通量小于实测数据.此外，仿真过程中对位移的取整会损失计算精度.敬明等[12]通过引入辅助变量及缩短仿真步长解决流量偏小及精度问题，本文考虑CAV和HV的特性，通过改进安全速度构建NaSch模型[13]，道路中第n辆车从时刻t到t+ 1时的演化规则[14]如式（3） ～ （8）所示.

加速规则：

减速规则：

随机慢化规则：

辅助变量更新：

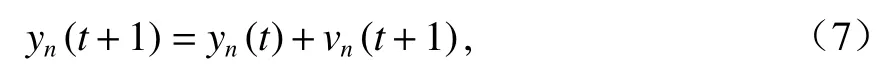
位置更新：

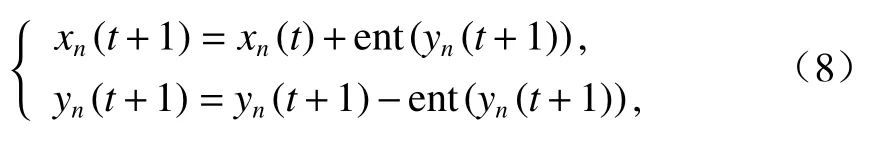
式（3） ～ （8）中：vmax为道路限速；vn,safe、an分别为第n辆车的安全速度和加速度，第n-1 辆车为前车；vn(t) 、xn(t) 分别为第n辆车在时刻t的速度和位置；yn(t) 为第n辆车在时刻t的辅助变量；bmax为最大减速度；R为车间通讯距离限制，取300 m.

1.3 数值仿真实验

为探究高速公路中异质流通行能力与CAV渗透率p间的关系，利用MATLAB对前期、中期及后期进行数值仿真.仿真参数为：道路长度为5 km，并采用周期性边界[15]，道路限速120 km/h，时间步长为0.1 s，仿真1 h，取最后600.0 s数据.车辆密度为0 ～ 120辆/km，为消除随机性误差，每个密度值仿真5次取均值.

由图1可以看出：三个阶段下，通行能力与CAV渗透率呈现正相关关系，渗透率提升，最大通行能力随之提升；道路上全为HV车辆时，最大通行能力仅为1 875辆/h；随着CAV渗透率的增加，前期能将最大通行能力提升至2 317辆/h，中后期能将最大通行能力提升至4 151辆/h.

图1 智能网联程度三阶段Fig.1 Three stages of intelligent network connectivity

道路中CAV车辆能在保证安全的前提下维持较小的车间时距，从而能在较大的密度下保持较高的速度，则CAV渗透率的增加能有效地提升道路通行能力.

各阶段下渗透率对于道路通行能力的提升如表2所示.

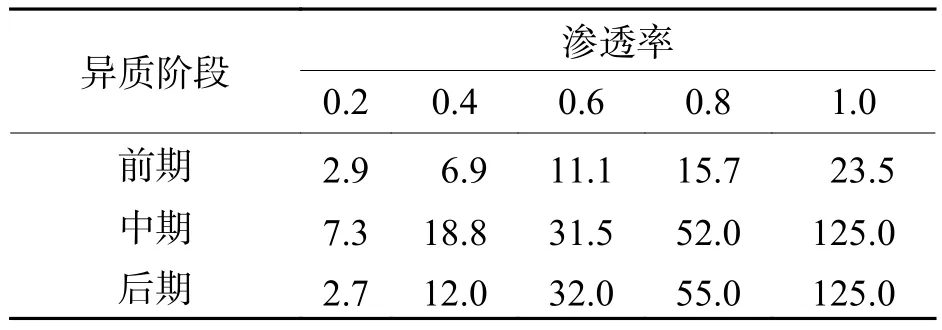
表2 通行能力提升程度Tab.2 Level of capacity improvement %

由表2知：随着CAV市场渗透率的增加，高速公路的通行能力提高；在异质流前期，最大提升程度仅为23.5%；在异质流中、后期，最大均能提升125.0%.另一方面，在渗透率0.2和0.4下，异质流中期的通行能力提升程度较前后期更优；在渗透率0.6和0.8下，异质流后期的通行能力提升程度较前、中期更优.可得出结论：在异质流中期，CAV车辆作为头车以ACC状态行驶时，能在低渗透下较好地缓冲CACC状态的CAV车辆与HV车辆，较好地提高道路通行能力，而在高渗透率下，ACC头车反而会制约CACC队列车对于道路通行能力的提升.

2 基于马尔可夫链的车辆排列

CAV市场渗透率增加与智能网联技术的发展并不是相互独立的，两者相互促进、共同提升.未来异质流将会经历低渗透率的前期，中等渗透率的中期和高渗透率的后期.由于现有HV车辆数量众多和机动车报废年限较长等原因，异质流将长期处于ACC、CACC和HV混合阶段，即异质流中期.该阶段异质流中的CAV车辆具有ACC及CACC两种跟驰状态，交通环境复杂，具有较高的实际研究价值，故下文选取该阶段为研究对象.

2.1 CAV与HV排列方式探讨

基于以上结论，随着CAV市场率的增加，道路通行能力有了明显的提升，如若改变CAV与HV车辆之间的排列方式，情况有所不同.CAV在相同交通流密度、相同渗透率（0.5）下依次按照混合态、分离态、随机态三种方式排列行驶，如图2所示.

图2 CAV与HV的排列方式Fig.2 Arrangements of CAV and HV

为探究不同排列方式下高速公路通行能力的变化规律，利用MATLAB接口分别初始化车辆排列方式为混合态、随机态和分离态，并进行元胞自动机仿真，仿真参数同1.3节，仿真实验结果如图3所示.

由图3可以看出：即便在同一渗透率下，当CAV与HV排列不同时，道路的最大通行能力仍具有显著差异，混合态、随机态、分离态三种方式对于通行能力的提升程度依次递增，最大通行能力分别为2 062、2 315、2 652辆/h，即CAV与HV的排列方式是影响通行能力的重要因素.

图3 不同CAV与HV排列下的流量Fig.3 Traffic flow under different arrangements of CAV and HV

进一步分析分离态和混合态的不同之处在于，分离态中存在大量CAV跟随CAV的行为（CAV跟随HV，HV跟随CAV忽略不计），混合态中存在大量CAV跟随HV和HV跟随CAV行为，两种状态内部车辆排列方式的不同导致了跟随行为的差异，从而有了通行能力的显著差异.由此知：CAV跟随CAV的状态能够较好地提升道路通行能力.

2.2 马尔可夫链的车辆排列探讨

针对异质流中车辆的跟随行为，可应用马尔可夫链理论进行探讨[16-17].假设所研究的单车道中车辆数为N，pH、pC分别为 HV、CAV 车辆的频率，则时，pC=p.单车道上第n辆车的概率取值矩阵

定义pC|H是第n辆车为HV的条件下第n+ 1 辆车为 CAV 的概率；pH|H、pH|C、pC|C的定义类推.

定义车辆类型的状态转移矩阵为

随机分布下，第n+ 1 辆车的类型与第n辆车的类型无相关性，即pC|C=pC|H=pC，pH|C=pH|H=pH.

定义F为车辆跟随行为的随机变量，fn为第n辆车的跟随行为，则fn∈SE，则跟随行为的概率取值矩阵为 πE，则

定 义pH-C|H-C为 在 上一 跟 随 行 为fn是fH-C的 条件下，下一跟随行为fn+1是fH-C的概率.同理：pH-H|H-H为在上一跟随行为fn是fH-H的条件下，下一跟随行为fn+1是fH-H的概率；pC-C|C-C为在上一跟随行为fn是fC-C的条件下，下一跟随行为fn+1是fC-C的概率.

可以得到跟随行为状态转移矩阵为

又因为

式中：P( ·) 为概率值.

所以 ，pH-C|C-C=pH|C.

fn+1=fC-H与fn=fC-C互斥，则pC-H|C-C=0.

同理，化简后可得

为验证式（14）的正确性，在随机态下通过仿真实验在100 km道路上随机生成10 000辆车，其中CAV的市场渗透率为0.2，仿真10 000次统计每次各跟随行为的出现频率，结果如图4、5所示.

图4 CAV-CAV频率Fig.4 Frequency of CAV-CAV

由图4可知：CAV-CAV跟随行为的频率在多次仿真下均能维持在0.04，其余跟随行为出现的频率同样能保持稳定.由图5可知：HV-HV出现的频率稳定在0.64，HV-CAV与CAV-HV的频率稳定在0.16，

图5 跟随行为频率Fig.5 Frequency of following behavior

当CAV的渗透率设置为其他值时亦符合上述结论，验证了马尔可夫推导正确性，则道路上出现CAV-CAV跟随行为的概率为，CAV-HV及HVCAV跟随行为的概率为pCpH，HV-HV跟随行为的概率为.

结合分离、混合和随机态仿真实验及马尔可夫理论可知：通行能力的增加不应归功于CAV市场渗透率的增加，而是因为当道路上的车辆类型服从随机分布时，渗透率的增加会导致更多CAV-CAV跟随行为的出现，使更多跟随车辆能够与前车形成协同自适应车队，能以更大速度，更小的车间时距行驶，从而使得通行能力的增加.

3 基于相对熵的队列研究

熵的概念是由德国物理学家克劳修斯于1865年所提出[18]，在热力学中有广泛的应用.随着统计物理、信息论等一系列科学理论发展，熵的本质才逐渐被解释清楚，熵是一个系统“内在的混乱程度”.

CAV异质交通流中HV与CAV的排列方式[19]可视为一个道路系统“内在的混乱程度”.研究交通流有序问题的一个基本条件是如何判断交通流的有序与无序[20-21]，这里基于马尔可夫链理论推导对CAV异质交通流进行有序的定义为：道路中所有车辆的跟随状态为CAV-CAV即有序.CAV异质流中出现越多的CAV-CAV跟随状态，则越接近有序状态.

相对熵（KL散度）是定量描述两个概率分布差异的一种方法，如若有序异质流与真实异质流中车辆跟随行为的随机变量F分别服从概率分布U和V，则可利用式（15）计算真实与有序异质流的差异程度，从而计算真实异质流的有序性.

式中：DKL为相对熵.

在未来智联网环境下，道路中CAV车辆的跟随状态可实时获取，得到CAV-CAV频率pC-C后利用式（16）计算V.根据异质流有序性的定义，异质流中所有车辆的跟随状态均为fC-C，利用式（17）计算U.

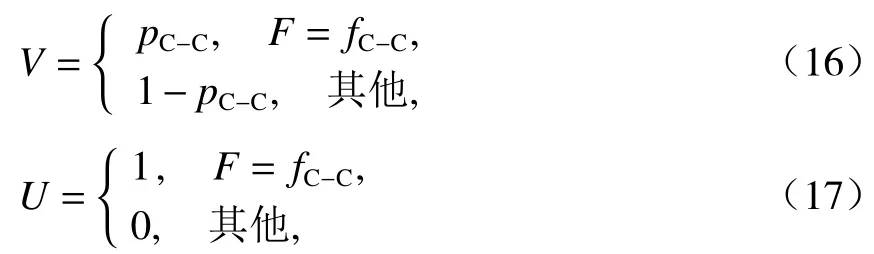
则异质流的相对熵为

在随机态中，CAV-CAV跟随状态的频率pC-C=pC|C=，则随机态的相对熵为

因为道路密度25辆/km时实验的流量数据良好，所以在该密度下进行相对熵的仿真实验.在仿真实验中可实时计算异质流跟随状态服从的概率分布V，代入式（18）计算异质流的相对熵.可得到如图6所示散点图，验证了随机态下式（19）的正确性及渗透率p与DKL的负相关关系.

同理随机态下，道路密度25辆/km时，仿真得到CAV渗透率与流量、相对熵与流量之间的关系分别如图7、8所示.

由图7、8知：相对CAV渗透率与流量呈现正相关，相对熵与流量呈现负相关关系；随机态中，同一密度下，CAV渗透率越大，相对熵越小，流量越大.因此，CAV渗透率的增加使得相对熵减小，异质流序列愈发“有序”使得交通流量增大.

图7 CAV渗透率与流量关系Fig.7 Relationship between CAV penetration and traffic flow

为探究相同渗透率下，不同相对熵值的道路通行能力.混合态在异质流中属于恶劣情况，CAV与HV都会主观避免该场景，故选取异质流中有理论研究价值及实际研究意义的随机态与分离态为研究对象，选择在0.2、0.4、0.6和0.8的CAV渗透率下进行异质流随机态与分离态的仿真实验，结果如图9所示.

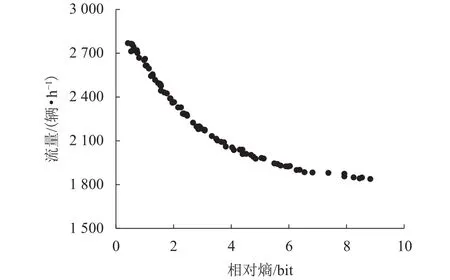
图8 相对熵与流量关系Fig.8 Relationship between relative entropy and traffic flow

图9 随机态及分离态的流量Fig.9 Traffic flows in random and separated states

仿真实验中，可通过实时检测异质流的跟随状态分布V，利用式（18）计算得到各渗透率下分离态与随机态的相对熵值，结果如表3所示.

由表3知：分离态异质流通行能力较随机态的相对熵更小，并且通行能力有了明显的提升：在渗透率为0.2时提升了24%；在渗透率为0.4时提升了19%；在渗透率为0.6时提升了12%；在渗透率为0.8时提升了5%.

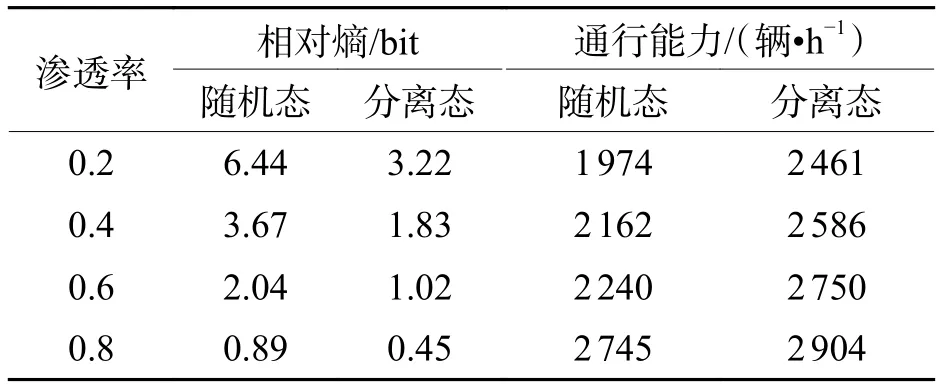
表3 随机态和分离态的通行能力及相对熵Tab.3 Capacity and relative entropy in random and separated states

综上，异质流通行能力的提升不应直接归功于渗透率的增加，其本质是渗透率的增加导致相对熵减小，车流序列趋于“有序”.此外，分离态较随机态的异质流相对熵更小，并能在通行能力上得到一定程度的提升，提升程度随着渗透率的增加而降低.

4 结 论

1） 在前期、中期及后期异质阶段下，CAV异质交通流的通行能力均会随着渗透率的增加而提升.前期CAV渗透率的增加对道路通行能力的提升并不明显，最多提升23.5%；中后期渗透率的增加能够最高能提升通行能力125.0%.

2） 异质流通行能力的提升本质是由于渗透率的增加导致相对熵减小，车辆间能形成队列以更小的车间时距行驶.

3） 相对熵能够定量描述CAV异质流的有序性，能够作为除速度、密度、流量之外的新参数描述交通流的状态，为CAV异质流的交通管理策略提供一定参考.