冰雪天气下基于MFOA-LSSVR的跑道温度预测

陈 斌，刘 悦，李庆真

(1.中国民航大学 电子信息与自动化学院，天津 300300；2.中国民航大学 航空地面特种设备研究基地，天津 300300)

在冬季，我国面向三北机场常常出现暴雪、积冰天气，经常导致航班延误、旅客滞留，甚至机场关闭。跑道除冰雪是航班保障的重要业务。而跑道温度是跑道结冰的重要因素，在一定时间范围内对跑道温度进行提前预测，将为跑道积冰预警提供有效信息，有助于机场提前对跑道积冰采取应对措施，以及高效地完成除冰作业。

多年来国内外学者对路面温度预测方法进行了大量研究，1957年Barber[1]最先利用路面介质温度周期变化热传导方程来描述路面温度变化规律。Kangas等[2]在芬兰地区建立了道路温度物理预测模型。邱金晶等[3]基于热量平衡方程建立了高速公路路面温度预测模型，模型预测结果准确度随着预测提前量的增加而逐渐降低。Sokol等[4]通过修正大气温度、大气湿度等边界条件建立了基于能量平衡和热传导方程的路面温度预测模型。Nuijten[5]基于太阳短波辐射通量和长波辐射通量等相关因素的能量平衡关系，建立了机场道面温度物理预测模型，该模型可以预测挪威奥斯陆机场整个冬季大部分时间的道面温度。王可心等[6]选用2015—2018年间宁宿徐高速公路上3个交通气象站的冬季路面温度观测资料，使用引入复合特征的随机森林回归模型对不同天气类型下冬季路面温度进行预测，预测结果显示雨雪天气下模型预测效果较好。Xu等[7]基于长期观测的路面温度，建立了一种改进的BP神经网络模型，并以不同日期和路段场景验证了预测模型的有效性。汤筠筠等[8]挖掘为期2个冬季高速公路路面温度与气温、相对湿度等气象因素之间的数据关系，建立自回归求和移动平均模型，用于预测冬季路面未来1 h温度，平均绝对误差达到0.15 ℃。综上可见，国内外对路面温度预测具有一定的研究基础，但当使用上述方法对冰雪天气下跑道温度预测时仍存在以下问题：① 考虑太阳辐射通量、大气长波辐射通量、路面材料性质能量平衡关系的道面温度机理预测模型建模过程复杂，导热微分方程在求解时需要做多种假设以简化边界条件，这将影响模型预测精度。② 使用时间序列、人工神经网络等方法建立的路面温度预测模型需要对路面温度进行长期观测。而冰雪天气下受天气情况、降雪时间和跑道周围环境变化等因素的影响，往往会使道面温度的幅值和周期性发生变化，使其呈现出短时序、小样本和非线性的数据特征。

最小二乘支持向量回归机(Least Squares Support Vector Regression,LSSVR)能够充分利用核函数的性质将输入数据映射到高维特征空间，将非线性数据变为线性可分，在解决小样本、非线性数据预测方面具有一定优势[9]。其中，核函数参数和惩罚因子对LSSVR的预测效果具有重要影响。果蝇算法(Fruit Fly Optimization Algorithm,FOA)具有计算速度快、求解精度高的特点，目前利用果蝇算法优化LSSVR的预测方法已经应用于天然气负荷预测[10]和汽轮机热耗预测[11]领域。但标准果蝇算法在参数寻优过程中易陷入局部极小值，这将对模型预测精度产生影响。鉴于此，本文针对冰雪天气下跑道温度预测问题，通过在模拟跑道实验平台中采集冰雪天气下跑道温度数据，提出一种基于改进的果蝇算法优化最小二乘支持向量回归机(MFOA-LSSVR)的跑道温度预测方法。

1 研究基础

为了反映冰雪天气下路面温度的变化情况，用模拟跑道道面实验平台对道面温度进行数据采集。冬季晴天和降雪2种不同天气类型下的4组道面温度数据如图1所示。由图1可得，在晴天天气下，道面温度具有明显的日变化特征，总体呈现先升后降的周期性变化特点，在上午10时左右有道面温度最低值，在午后有道面温度最高值。在冰雪天气下，道面温度降低，波动平缓，不再表现出周期性的日变化特征。因此针对冰雪天气下的道面温度数据特征需要建立基于MFOA-LSSVR的道面温度预测模型。

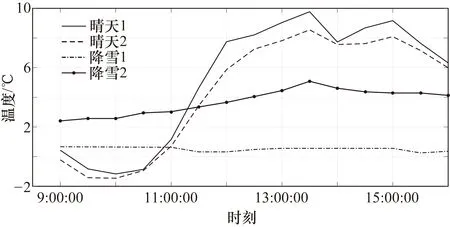
图1 冬季不同天气类型下的道面温度

1.1 Spearman相关性分析

跑道暴露于外界自然环境中，跑道道面温度的变化是一个受气象条件、路面材料和不同地基温度等多个影响因素相互耦合的复杂过程，深度挖掘冰雪天气下道面温度与周围可量化监测的主要影响因素之间的相关性，能够为跑道温度短时预测提供关键信息。Spearman相关系数是统计学中一种评估特征与目标变量相关性强弱的重要指标[12]。其基本定义为：对2个m维变量A={a1,a2,…,am}和B={b1,b2,…,bm}按照从小到大的方式排序，由排序前后A、B变量中元素的变化位置，可以计算差分集合di，1≤i≤m，由此确定Spearman相关系数为

(1)

ρ(A,B)的绝对值在[0,1]之间，绝对值越大表示变量间相关性越强。当ρ(A,B)值为正时表示正相关，为负时表示负相关。

1.2 最小二乘支持向量回归机

最小二乘支持向量回归机的优化函数为

(2)

式中：w为权向量；ξ为惩罚因子；ek为松弛变量；N为样本数；φ(x)为非线性映射函数；b为偏置量。由拉格朗日乘子ak和KKT(Karush-Kuhn-Tucker)优化条件求解式(2)得LSSVR最终优化函数表达式为

(3)

式中：k(x,xi)取径向基函数(Radial Basis Function,RBF)，即

(4)

当采用RBF训练LSSVR时，核函数参数σ与惩罚因子ξ对模型预测性能具有重要影响，因此本文采用改进的果蝇算法优化LSSVR核参数。

1.3 改进的果蝇优化算法

果蝇算法是由Pan[13]提出的一种基于果蝇觅食行为寻找全局最优解的群体新智能方法。但标准果蝇算法的搜索半径为[0，1]之间的随机值，搜索半径过小易使果蝇种群迭代变慢，陷入局部最优。因此本文对标准的果蝇算法进行改进，采用指数函数α更新果蝇搜索半径，并引入距离扩充因子a0实时更新果蝇位置，从而提高果蝇的全局寻优能力和预测精度。改进果蝇算法(Modified Fruit Fly Optimization Algorithm,MFOA)的具体步骤如下。

① 初始生成果蝇种群规模和最大迭代代数，设置果蝇群体初始位置为X0和Y0。

② 随机设定果蝇搜索步长，更新果蝇位置。

(5)

式中：X1，Y1为果蝇个体的更新位置；Random∈[0,1]。

③ 计算果蝇味道浓度判定值Si。

(6)

S=1/D

(7)

(8)

α=λβg

(9)

(10)

Si=1/Di+a0·Di

(11)

a0=b0-Random

(12)

式中：g为果蝇迭代代数；λ，β，b0为常数。

④ 将S带入适应度函数中，可得每只果蝇个体的味道浓度值Smell(i)，通过对比找到果蝇种群适应度函数值最小的个体。

Smell(i)=Fitness(Si)

(13)

[bestSmellbestIndex]=min(Smell(i))

(14)

⑤ 保留最佳味道浓度值和x、y坐标，果蝇群将以最佳浓度个体为目的地前往飞行。

Smellbest=bestSmell

(15)

(16)

⑥ 迭代寻优，重复执行步骤②～步骤⑤，若味道浓度优于前一迭代浓度，则迭代停止。

2 基于MFOA优化的 LSSVR 预测模型

图2为MFOA优化LSSVR流程图。

图2 MFOA优化LSSVR流程图

将当前时刻道面温度和道面温度主要影响因素共同作为预测模型的输入特征，道面未来10 min温度为预测模型的目标输出。将样本数据按照9:1划分为训练集和测试集，以均方误差为适应度函数，其计算式为

(17)

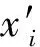
3 实例仿真及分析

3.1 数据采集

本文样本数据通过模拟跑道实验系统平台采集获得，模拟跑道实验系统平台如图3所示。根据MH/T 5004—2010《民用机场水泥混凝土道面设计规范》设计水泥混凝土道面[14]，并将ARS31Pro道面温度传感器嵌入水泥跑道道面，3个相同规格的PT100分别嵌入道面下方10 cm、20 cm、40 cm处，依次用于测量道面温度和道面下方10 cm、20 cm、40 cm深度温度。在跑道周围放置Vaisala WXT520气象传感器和湿度传感器，用于测量风速、大气温度、大气湿度、大气压强和露点温度。其中ARS31Pro道面温度传感器测量精度为±0.2 ℃，PT100测量精度为±0.1 ℃，风速测量精度为±0.3 m/s，大气温度测量精度为±0.3 ℃，大气湿度测量精度为±3%，露点温度测量精度为±0.2%，大气压强测量精度±1 hPa。数据采集间隔为1 min。选取2020年1月5日、2020年11月21日和2021年11月8日3组降雪天气的跑道温度实测数据作为实验样本1～样本3。部分样本数据如表1所示。

图3 模拟道面采集实验平台

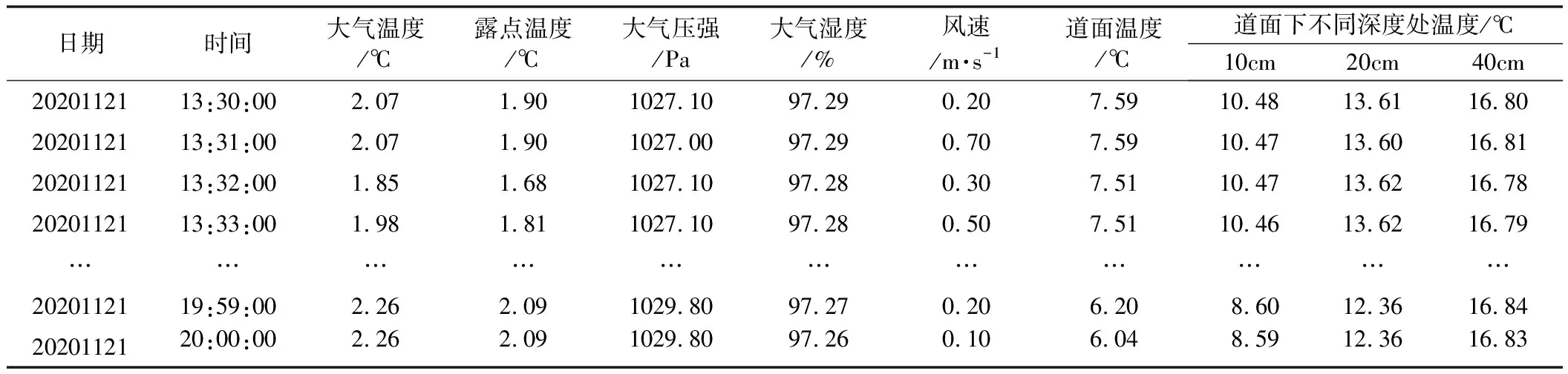
表1 部分样本数据

3.2 归一化处理

为避免各特征变量由于单位和量纲差别对模型预测精度产生影响，采用最小最大法将样本数据归一化到[0,1]区间，计算公式为

(18)

式中：xmin为样本数据最小值；xmax为样本数据最大值；x1、x0分别为样本数据归一化前后的值。

3.3 跑道温度Spearman相关性分析结果

道面温度与各影响因素的Spearman值如表2所示。由表2可知，冰雪天气下道面温度与大气温度、露点温度呈正相关，与风速和大气压强的相关性不强。其中，与大气温度相关性最高，达到0.88，露点温度次之。当大气温度和露点温度越低时道面温度随之降低。另外，道面温度与大气湿度呈负相关，即湿度越大道面温度越低。道面温度与不同深度处地基温度均具有一定相关性，随地基深度增加相关性逐渐减弱。综上，选取Spearman相关性较强[12]的影响因素为LSSVM模型的输入特征变量，即露点温度、大气温度、大气湿度和道面下方10 cm温度。

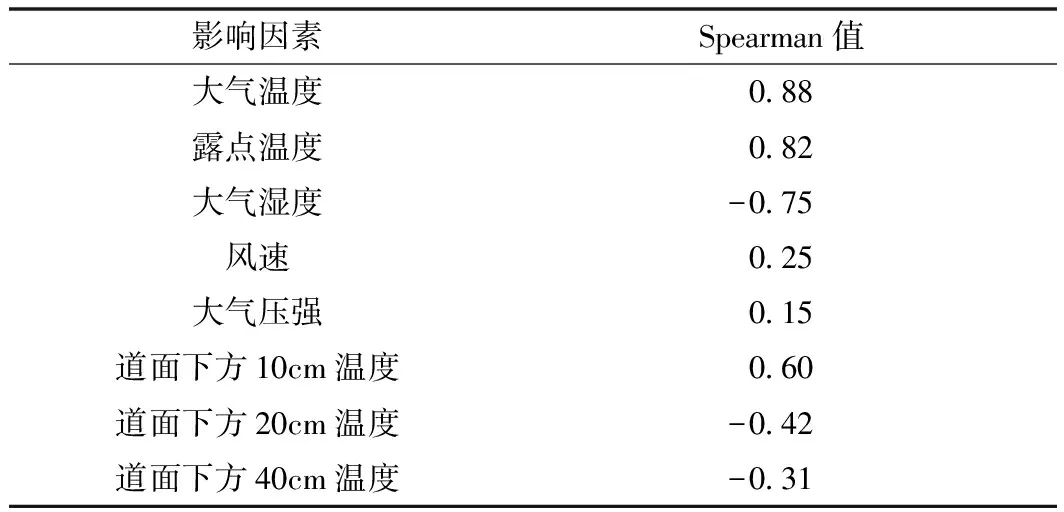
表2 相关性结果

3.4 模型评价指标

选用平均绝对误差(Mean Absolute Error，MAE)对MFOA-LSSVR模型的预测误差进行评估分析。其中，MAE数值越小,表明模型的预测误差越小。计算公式为

(19)

3.5 跑道温度预测结果及分析

设置果蝇算法种群规模为10，迭代代数为50，λ=0.5，β=1.1，b0=0.9。核函数参数σ和惩罚因子ξ的取值范围为[0,10]和[0,100]。以均方误差最小为优化目标，获得MFOA-LSSVR模型预测值。为验证MFOA-LSSVR模型预测效果，将其与跑道温度的FOA-LSSVR、BP神经网络和机理模型[15]的预测结果进行对比分析。上述4种模型的预测MAE值如表3所示，预测结果如图4所示。

表3 不同类型预测平均绝对误差

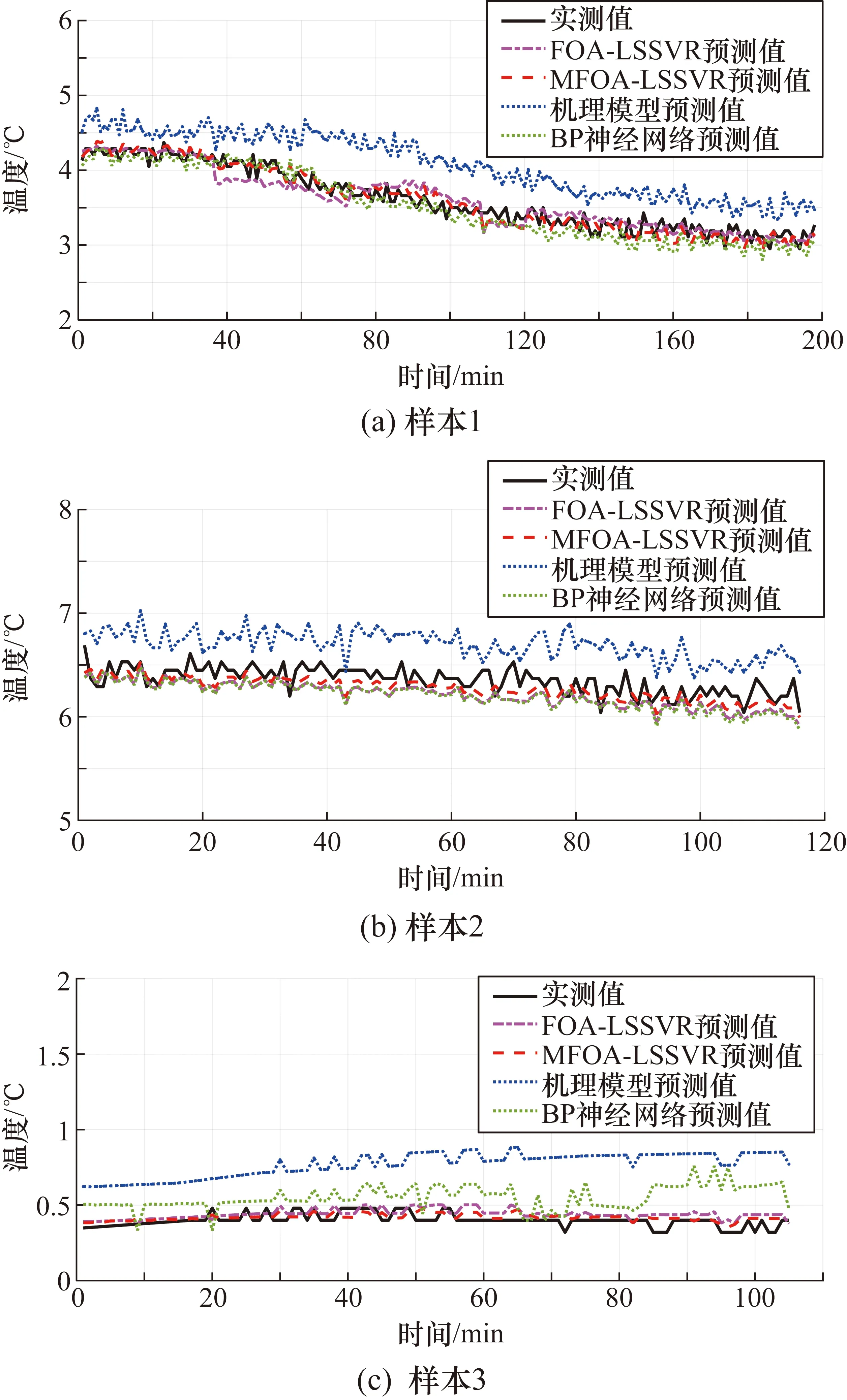
图4 不同模型的预测结果

从表3可以得出，在3组样本中，MFOA-LSSVR模型的MAE值均为最小。与FOA-LSSVR模型、机理模型、BP神经网络相比，MFOA-LSSVR模型的MAE值至少可以分别提升了17.24%、69.76%和25.37%。可见使用MFOA会使LSSVR的核参数具有更高的全局寻优能力，从而使预测精度更高。通过深度挖掘当前时刻大气温度、露点温度、大气湿度、道面温度与道面未来时刻温度之间的内部关联信息，可以提高模型整体预测效果。在图4中，与FOA-LSSVR、机理模型、BP神经网络的预测值相比，MFOA-LSSVR预测值与道面温度实际值最接近。可见MFOA-LSSVM模型能更准确地预测道面未来时刻温度的变化规律，预测效果更好。

为验证添加主要影响因素作为输入特征对道面温度预测结果的影响，将上文建立的MFOA-LSSVR多变量预测结果与仅将道面温度作为输入特征的预测结果进行对比分析。基于MFOA-LSSVR多变量与单变量预测MAE值如表4所示。

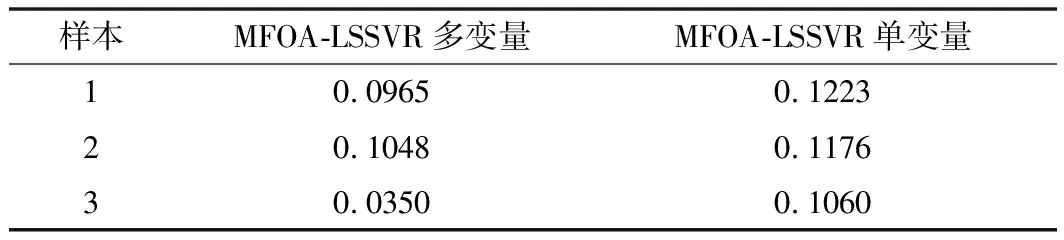
表4 基于MFOA-LSSVR多变量与单变量预测MAE值

从表4可得出，与MFOA-LSSVR单变量预测结果相比，MFOA-LSSVR多变量模型具有更小的MAE值，分别提高了21.10%、10.88%和66.98%。可见考虑道面主要影响因素的预测效果好于单独仅将道面温度为特征变量的预测效果。说明在冰雪天气下道面温度预测过程中，跑道周围主要气象因素与地基温度因素对道面温度具有重要影响，将其作为输入特征能够有效提高模型预测精度。

4 结束语

建立了基于MFOA-LSSVR的冰雪天气下跑道温度预测模型，以实测数据验证了引入指数更新函数和距离扩张因子的改进果蝇算法的有效性，能够增强标准果蝇算法对LSSVR核参数和惩罚因子的寻优性能，提高模型整体的预测精度。

将大气温度、露点温度和大气湿度等影响跑道温度的主要因素添加为道面温度输入特征，能够有效地提高MFOA-LSSVR模型的预测精度。

该跑道温度预测方法能够为跑道积冰预警提供有效信息，目前该方法已在模拟道面上进行预测验证，后续研究将考虑建立面向实际机场的跑道温度在线预测模型。