高速离心泵叶轮动态特性分析

2022-08-25王彦伟朱启培李育房

流体机械 2022年7期

王彦伟，朱启培，2，李育房

（1.武汉工程大学化工装备强化与本质安全湖北省重点实验室，武汉 430205；2.杭州海康威视数字技术股份有限公司，杭州 310052）

0 引言

离心泵在启动过程中由于转速和流量不是直接达到额定值，而是伴随一个攀升的过程，在此过程中叶轮受力不均极易发生振动失稳。在离心泵正常工作中，其内部流场也不是均匀流动的，流场中产生的流体力包括流动脉动、旋转空化等，还包括由吸入室、排出室等干涉引起的流体力以及叶片与隔舌之间的动静干涉引起的流体力，伴随着这些流体作用力强迫叶轮发生振动，时刻对叶轮产生冲击，诱导叶轮产生振动。

目前国内外对离心泵叶轮动态特性研究主要有：ZHU等［1］采用外特性试验以及非定常数值模拟方法对离心泵启动过程中的外部流动特性进行分析，发现离心泵在启动过程中流动速度大小与压力大小随时间而线性增加，并随着叶轮转速升至额定转速，其内部流速与压力趋向稳定；杨敏官等［2］通过对离心泵进行非定常数值模拟计算，研究离心泵内部流场流动变化规律，发现离心泵叶轮在不同工况下所表现出的变化规律相似，其频域上叶频对叶轮影响较大；施卫东等［3］通过选取不同的离心泵基圆半径对所受径向力进行研究，并得出了离心泵不同工况下径向力的变化规律；PAVESI等［4］采取实验的方法对离心泵内部非定常流动的压力脉动频率特性进行分析，发现叶轮出口交界面处的压力分布具有非对称性动；YUAN等［5］对离心泵进行非定常流动及其压力脉动分析，发现叶轮出口附近的压力脉动是具有周期性的，所产生的波动峰值与叶片数相一致，其压力脉动频率与叶片的通过频率相同。总体来看，国内外学者对离心泵动态特性研究较为广泛，但针对高速离心泵启动过程中叶轮的动态特性以及内部非定常流动诱导叶轮振动的研究极少。

本文主要研究内容为：利用Creo软件对离心泵结构及其流道模型建立，通过Flomaster软件搭建离心泵仿真实验平台，得出离心泵启动过程中转速和流量变化规律，并将其加载到离心泵模拟计算中，通过单向流固耦合方法分析出离心泵启动过程中叶轮动态特性。而后计算分析了离心泵在不同工况下稳态径向力，得出叶轮所受径向力与流量的变化规律，以及非定常流动下叶轮所受瞬态径向力与时间的变化规律，离心泵叶轮在只考虑径向力作用下的振动特性，得出叶轮在径向力作用下容易发生振动失稳的频率。

1 数值方法

流固耦合计算包括单向流固耦合和双向流固耦合，单向流固耦合即考虑流体作用力对结构的作用，而不考虑结构的变形反作用于流体［7］，这种方法适用于结构刚度大，不易发生变形的结构以及流体冲击力不大的情况，而双向流固耦合考虑结构变形对流体的影响，适用于结构易发生变形的计算。本文所选离心泵材质为钛合金，结构刚度大，变形微小，对流体影响可以忽略，故本文采用单向流固耦合方法来探究流体对结构的影响。单向流固耦合作用机理如图1所示。

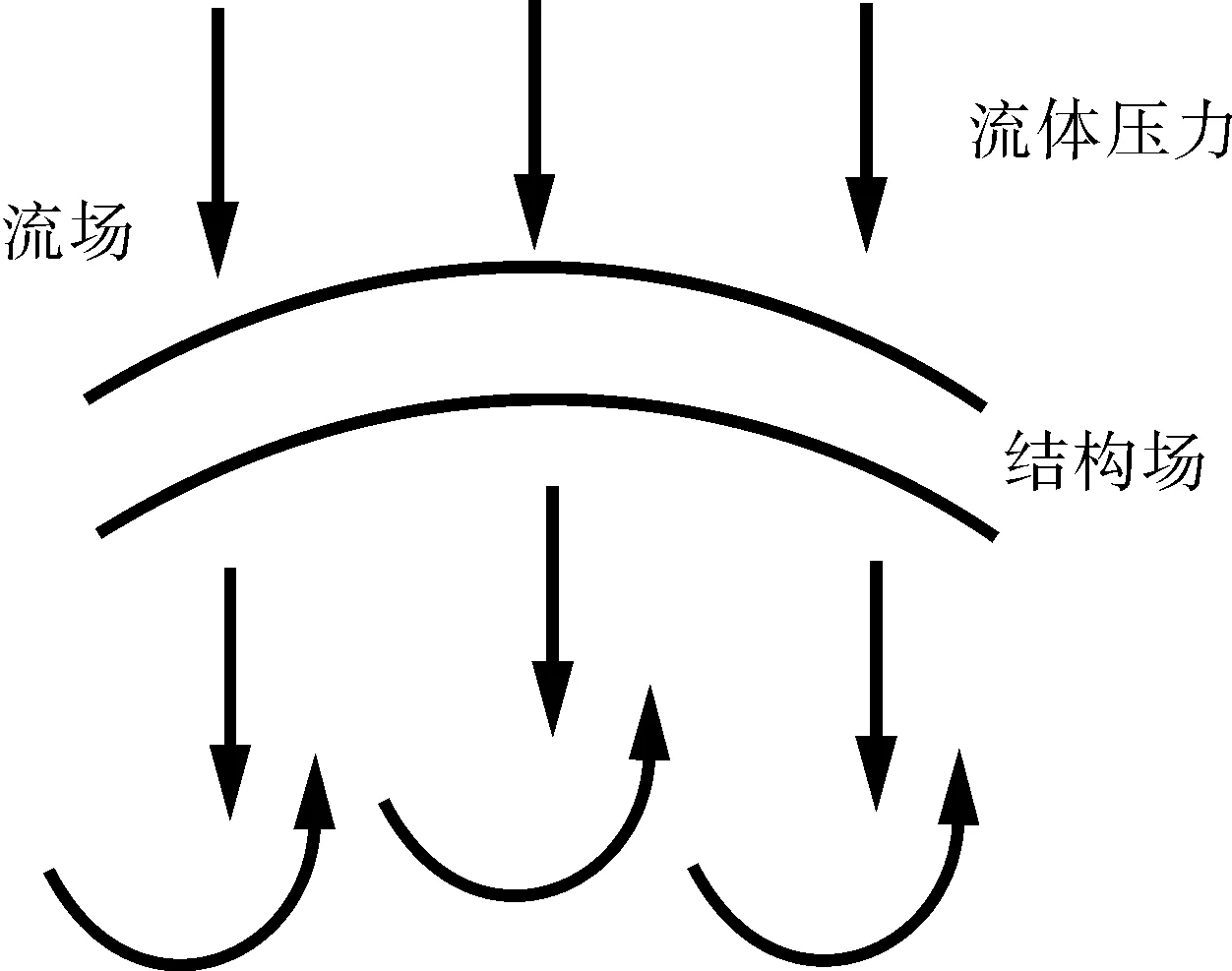
图1 单向流固耦合作用机理Fig.1 Mechanism of unidirectional fluid structure interaction

针对离心泵叶轮所受径向力计算方法采用直接计算法，蜗壳内流动的不对称性和叶轮出流的不均匀性导致叶轮出口附近静压分布不均匀，这是产生径向力的根本原因［8］。离心泵流场结果采用计算流体动力学（Computational fluid dynamics，CFD）数值模拟方法得出，其叶轮受到的压力与黏性力是由流体作用下产生的，是导致径向力产生的主要因素［9-12］。通过编辑CEL表达式，计算叶轮与蜗壳交界面节点在X和Y方向所受到的压力与黏性力和叶片及其叶轮前后盖板在X和Y方向所受压力分力大小，运用力的合成定理得到叶轮所受径向力。其CEL表达式如下：

X方向上的分力：

force_x@Impeller_Shroud+force_x（@Impeller_hub+force_x@Impeller_Blades+force_x（@Interfacel+force_x@Interface2

Y方向上的分力：

force_y@Impeller_Shroud+force_y（@Impeller_hub+force_y@Impeller_Blades+force_y（@Interfacel+force_x@Interface2

径向力的合力：

（force_x^2+force_y^2）^（1/2）

2 离心泵启动过程中叶轮动态特性分析

2.1 模型的建立

本文所选离心泵型号为Q25H52，流量Q=25 m3/h，转速 n=6 100 r/min，扬程H=52 m，叶轮进口直径D1=44 mm，出口直径D2=100 mm，出口宽度b2=8 mm，叶片数Z=6，泵的介质密度为ρ=1 200 kg/m3，材质为钛合金，其性能参数见表1，通过Creo软件对离心泵模型进行三维建模，并导入workbench DM划分出流场模型。

表1 叶轮材质性能参数Tab.1 Impeller material property parameters

2.2 网格划分

采用非结构性网格对离心泵流体域进行划分，对蜗壳隔舌处、叶片采用更高密度的网格，对划分好的网格进行无关性验证，在保证网格划分精确性的同时尽可能地降低计算所占用计算机的资源。如表2所示，以离心泵扬程大小为依据对网格大小进行无关性验证，方案3比方案2全流道网格单元数多出接近1倍，而扬程大小仅增大0.1 m，故最终网格选取方案2进行划分，划分后全流道网格模型如图2所示。

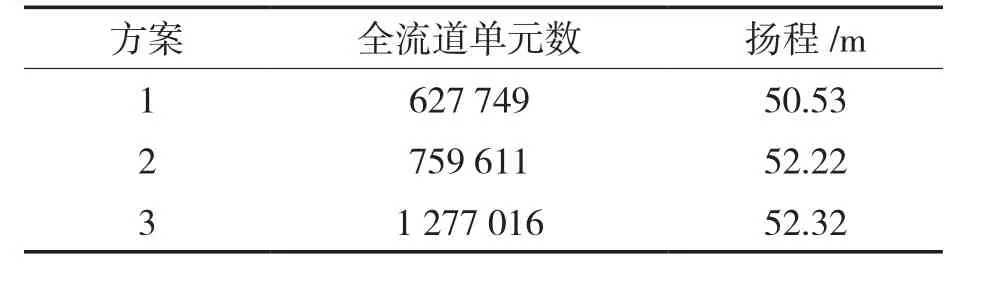
表2 网格无关性验证Tab.2 Grid independence verification

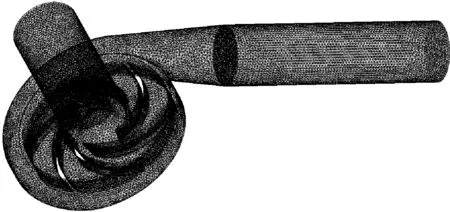
图2 离心泵全流道流场网格模型Fig.2 Grid model of flow field in the whole flow passage of centrifugal pump

2.3 Flomaster仿真实验

通过Flomaster软件搭建仿真实验平台，如图3所示，由离心泵、刚性管、阀门、蓄水池、信号发生器以及仪表模板连接而成，通过设置各部件参数，运行得到离心泵启动过程前2 s电机转速和流量随时间变化数据，如图4所示，离心泵在启动过程中转速和流量并不是一开始直接达到额定转速和额定流量，而是经历一个变化的过程，转速和流量先是快速增大直至超过额定转速和额定流量数值，而后开始下降，呈现出一个波浪式变化，并在额定转速和额定流量附近保持相对稳定。

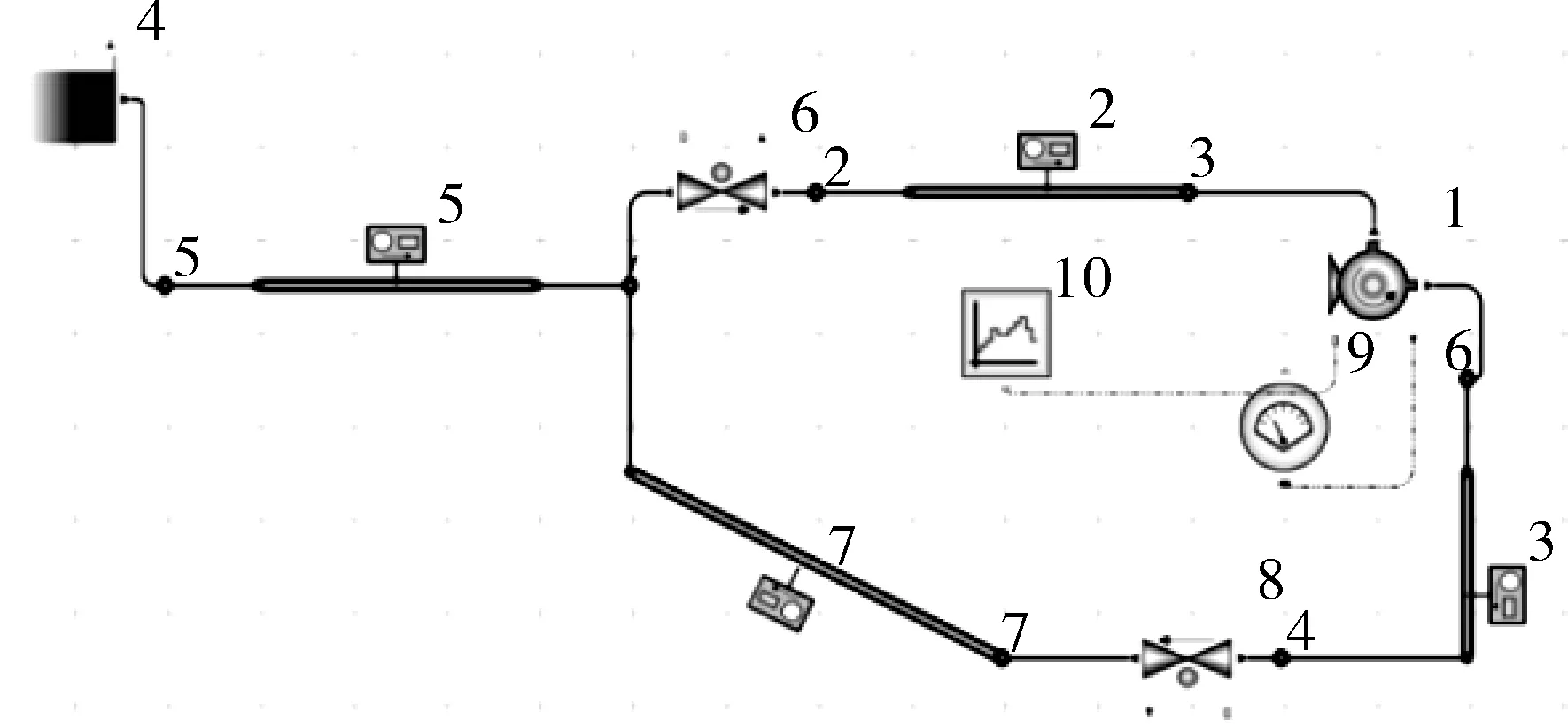
图3 离心泵Flomaster仿真实验平台Fig.3 Flomaster simulation experiment platform of centrifugal pump

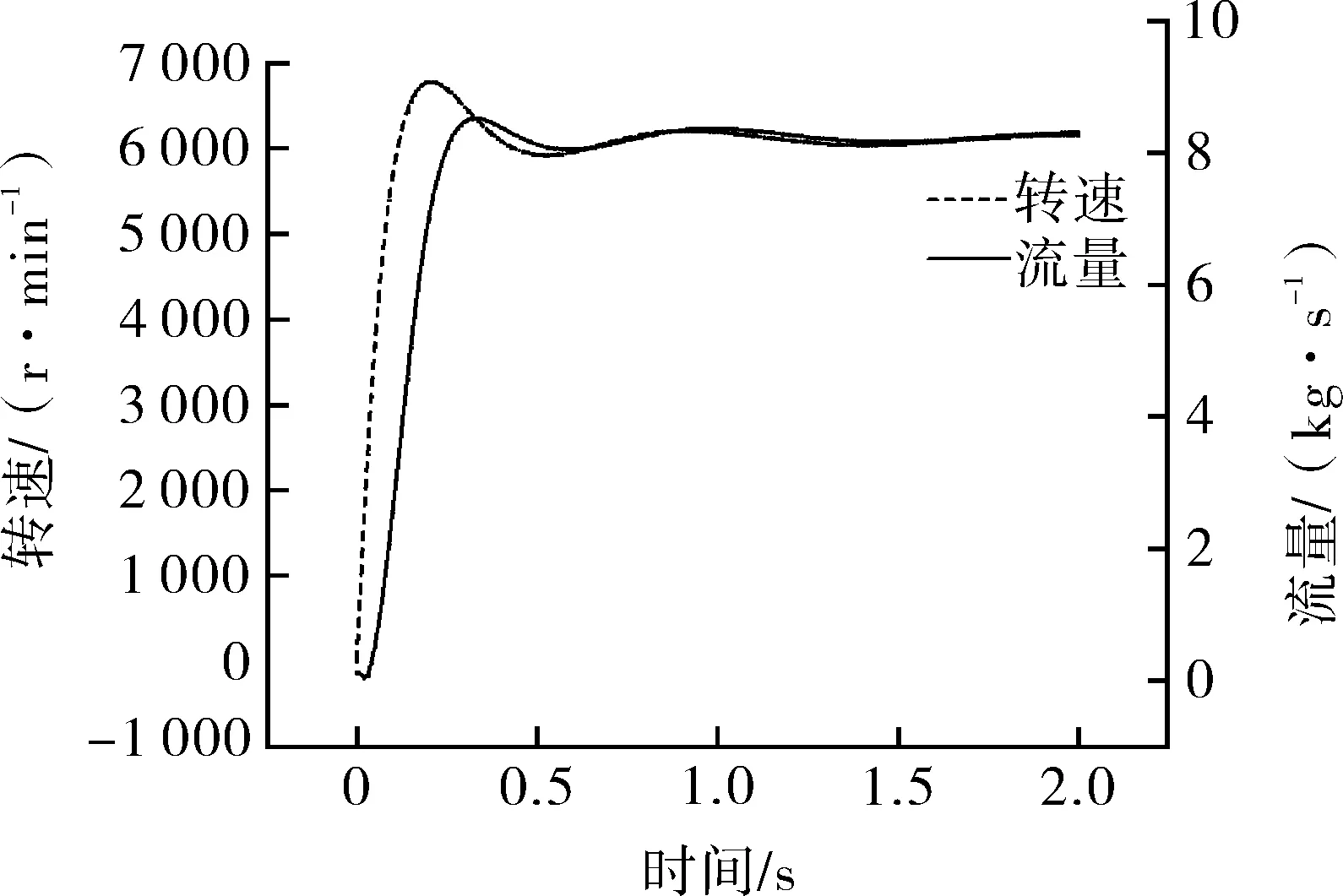
图4 离心泵启动过程转速和流量变化曲线Fig.4 Speed and flow curve of centrifugal pump during startup

2.4 启动过程中叶轮振动分析

在离心泵的实际运行中，径向力是造成振动的主要原因［13-18］，通过单向流固耦合方法分析叶轮在启动阶段振动特性。离心泵启动过程属于瞬态流动分析，在CFX流场计算中，设置时间步长为0.005 s，计算总时长为2 s，每个时间步保存一次，一共保存400个结果。图5示出了叶轮固体域瞬态分析设置方法，其时间步长与总时间必须与流场中的设置保持一致，以便于流体与固体间的耦合，设置叶轮前后盖板内表面以及叶片表面为流固耦合面，并对叶轮进行圆柱约束，转速的设置是由第2.3节得到的转速随时间变化的数据，将其进行Matlab曲线拟合得到转速随时间变化公式，以时间为变量的函数作用到离心泵启动过程仿真中。

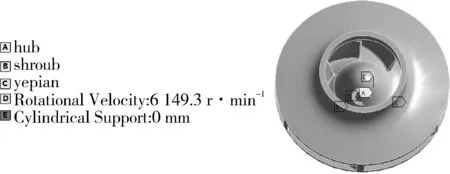
图5 叶轮启动过程中固体域设置Fig.5 Solid domain setting during impeller startup

求解得到离心泵启动过程叶轮所受径向力变化曲线，如图6所示，离心泵在启动阶段叶轮所受径向力是不均匀变化的，在启动过程0.1 s内，离心泵叶轮所受瞬态径向力整体上呈现剧烈上升趋势，最大值接近 300 N，在 0.1 s＜t＜0.3 s内，叶轮瞬态径向力呈现短暂下降，在0.3 s之后，随着转速和流量逐渐接近额定工况，叶轮流道内液体压力保持相对稳定，所受瞬态径向力在30 N附近稳定波动。

图6 离心泵启动过程中叶轮瞬态径向力曲线Fig.6 Transient radial force curve of impeller during centrifugal pump startup

在瞬态叶轮结构域查看结果，可以得到离心泵启动过程中叶轮动态特性的变化情况。如图7所示，离心泵启动过程中叶轮所受幅值大体上先急剧增大后趋于平稳，尽管在0.25 s＜t＜0.5 s略有减小，后又恢复平稳。在启动期间的0.25 s内，叶轮整体振动幅值呈现急剧上升趋势，最大值0.013 mm，在0.6s内，叶轮振动幅值呈现剧烈波动，在0.25 s＜t＜0.5 s，叶轮振动幅值呈现出下降趋势，在0.6 s之后，随着叶轮所受径向力趋于稳定，叶轮振动幅值逐渐保持稳定，并在0.01 mm处稳定性波动，波动范围在0.009～0.011 mm之间。

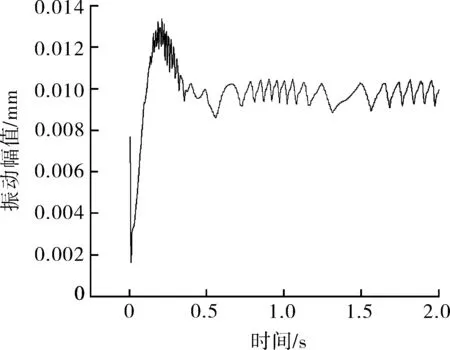
图7 离心泵启动过程中叶轮振动幅值曲线Fig.7 The vibration amplitude curve of the impeller during the startup process of the centrifugal pump

图8（a）示出了离心泵启动过程中叶轮加速度变化情况，加速度首先在0.2 s内迅速增大到4 000 mm2/s，由于时间较短，速度变化较小，在0.2 s＜t＜0.25 s内加速度迅速降至 500 mm2/s，之后随着径向力稳定性波动，加速度趋于较为稳定阶段，波动范围在0～2 000 mm2/s之间。离心泵启动过程中叶轮速度变化情况如图8（b）所示，叶轮的速度大小在整个启动过程内剧烈波动，从离心泵启动后速度在0.13 s内迅速达到最大值10 mm/s，之后在 0.13 s＜t＜0.25 s内速度又迅速下降至1.8 mm/s附近，0.25 s之后随着叶轮加速度大小趋于平稳，叶轮速度波动范围减小，波动范围在0～5 mm/s之间。通过对离心泵启动过程叶轮动态特性的分析，可以发现其变化规律与启动过程中叶轮瞬态径向力变化规律相似，这也表明了叶轮所受径向力是造成叶轮振动的主要原因。

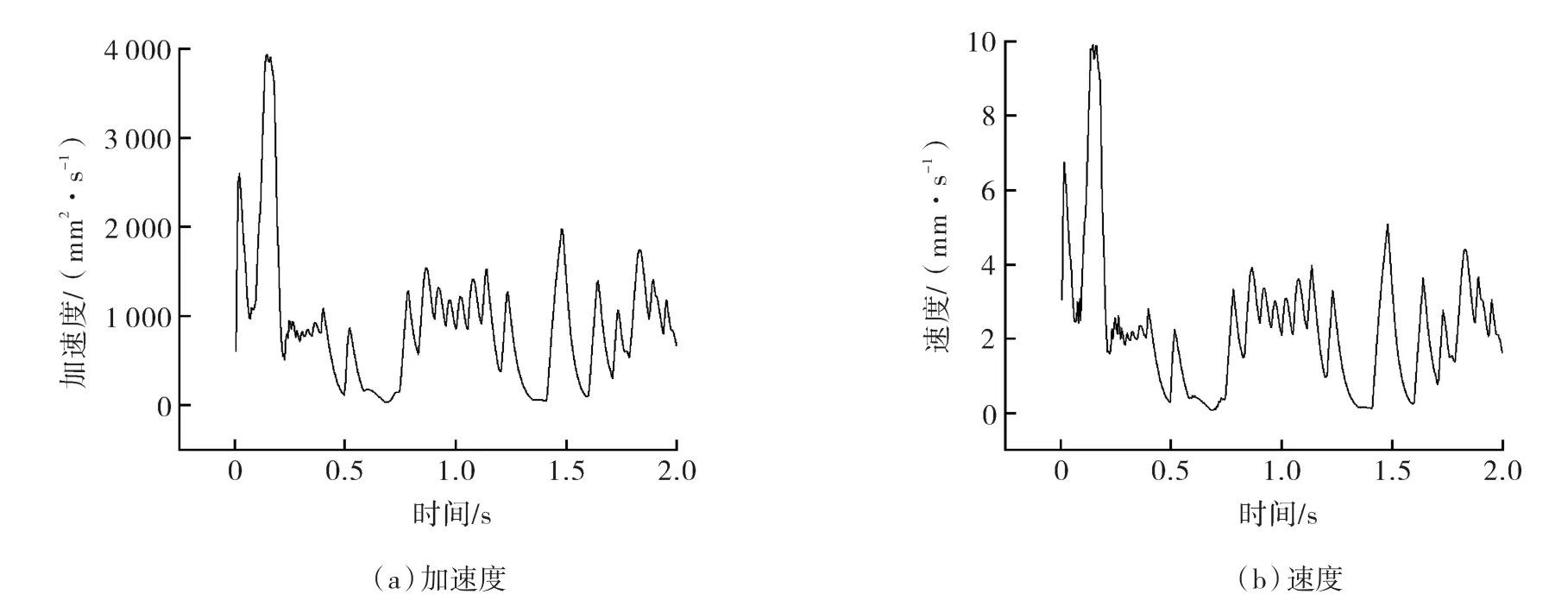
图8 离心泵启动过程中叶轮动态曲线Fig.8 Dynamic curve of impeller during startup of centrifugal pump

3 非定常流动诱导叶轮振动分析

3.1 稳态径向力分析

通过CEL表达式计算得出5种工况下总径向力的X和Y分量的大小和方向和总径向力的大小和方向。

由模拟计算得出，不同设计工况下，径向力随着流量的变化趋势，如图9（a）所示。从图中可以看出：在设计工况时径向力并不为零，其原因是离心泵本身结构存在不对称性，流体从叶轮流出后压力在周向方向上分布不均匀，致使叶轮内部流体流速以及流量存在不对称性，导致叶轮所受径向力不为零。所受径向力在设计工况时最小，在偏离设计流量时，径向力变大，并且偏离设计流量越大，径向力就越大。

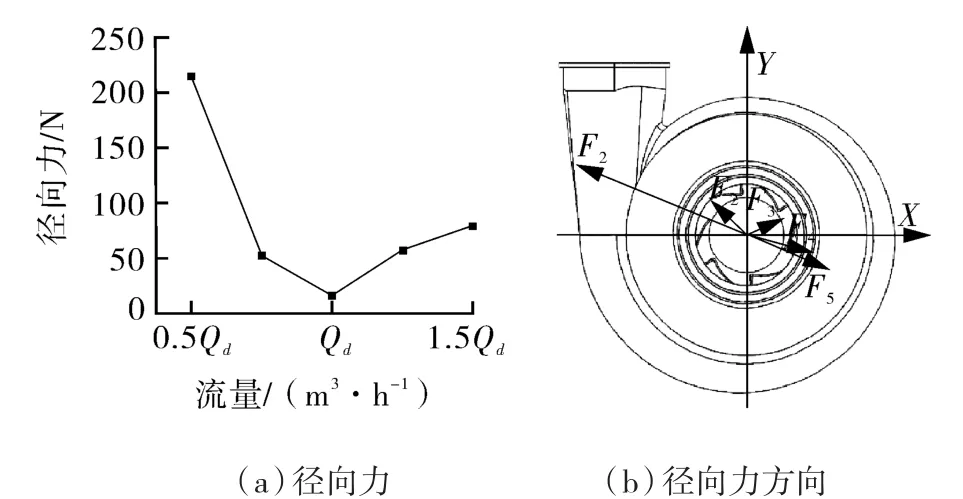
图9 不同工况下稳态径向力分布Fig. 9 Steady radial force distribution under different working conditions

计算得出不同工况下径向力的矢量坐标，图9（b）中 F1，F2，F3，F4，F5分别为离心泵在 0.5Qd，0.8Qd，Qd，1.2Qd，1.5Qd工况下叶轮所受径向力方向分布，径向力的大小和方向都随着流量的变化而发生改变。在大流量工况下，1.5Qd，1.2Qd流量时径向力的矢量在直角坐标系中的第四象限；在小流量工况下，0.5Qd，0.8Qd时，径向力在第二象限，在设计流量工况时，径向力并不为零，方向在第一象限。

3.2 叶轮振动分析

3.2.1 瞬态径向力计算与分析

在3.1节中通过研究不同工况下径向力随流量变化情况，模拟出径向力随流量变化的函数，对径向力的求解属于平均算法，并不能反映叶轮所受径向力与时间的关系，而叶轮振动是随时间变化的动态过程，在实际工作状态中，离心泵内部流动属于非定常流动，叶轮所受径向力是时间的函数。通过对离心泵进行非定常模拟，在每个时间步上保存结果，得到叶轮所受径向力与时间的函数关系。

对离心泵在小流量工况0.8Qd、标况Qd和大流量工况1.5Qd下分别进行非定常数值模拟计算，得到叶轮旋转6周内的径向力的变化情况。设置叶轮每转过15°为1个计算1个时间点，即为1个时间步长。本文叶轮转速是6 100 r/min，所以叶轮旋转1周是24个时间步长，即时间步长等于叶轮旋转周期的1/24，所以叶轮旋转周期是0.009 836 s，时间步长等于0.009 836 s/24=0.000 41 s，经过迭代，得到每一个时间步长都达到收敛。在每个时间步长上计算叶轮所受径向力，并在每个时间步上保存一次结果，由此得到径向力与时间的变化关系，如图10所示，叶轮所受径向力呈现出周期性变化，在1个旋转周期内出现6个峰值，这与叶轮旋转1周内叶片扫过蜗壳隔舌处的次数相等，表明叶片与蜗壳隔舌处有着剧烈的动静干涉作用，在标准工况下，叶轮旋转1周内各时刻所受径向力最小；非标准工况下，偏离标准流量越大，叶轮在各个时刻所受径向力越大，这与稳态计算时径向力与流量的变化规律相一致。

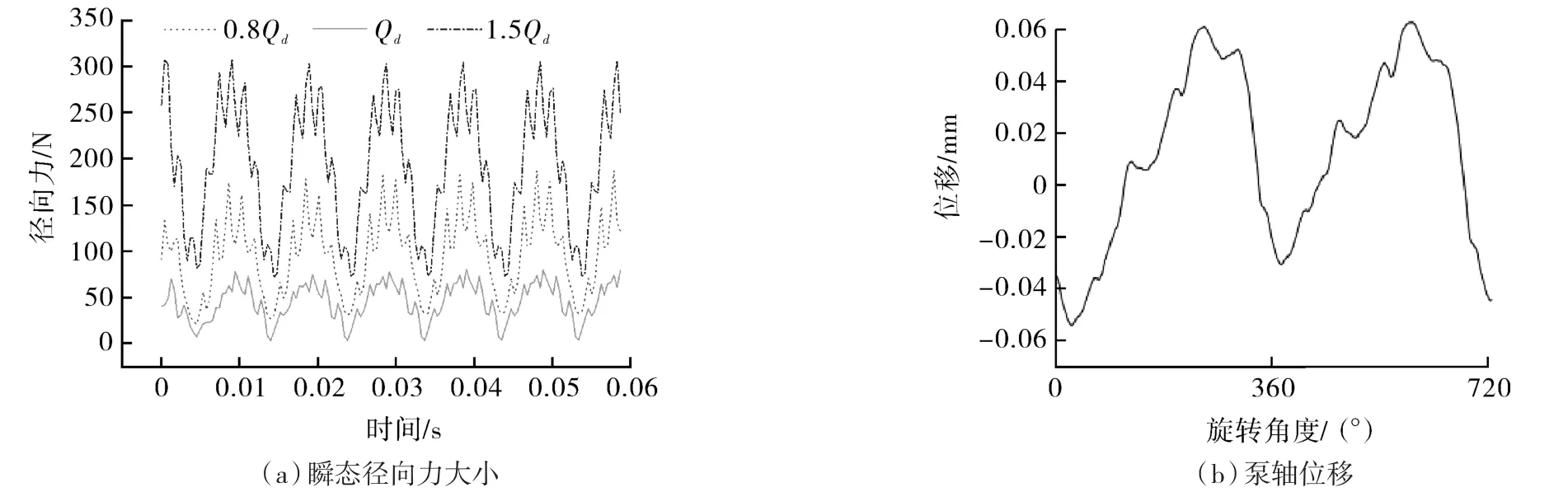
图10 仿真与试验结果波形变化规律对比Fig.10 Comparison of waveform changes between simulation and test results

3.2.2 结果验证

为了验证叶轮所表现出动态变化的准确性，根据学者张鑫［18］采用电涡流位移传感器对离心泵转子进行振动试验研究的结果，如图10（b）所示，即：试验测量出泵轴振动位移所表现出来波形的变化规律与叶轮所受瞬态径向力表现出来的波形规律大致相同，导致泵轴位移变化的力即为叶轮所受径向力。由此，经对比图10（a）（b）的波形图变化规律可知，本文瞬态径向力变化规律与试验结果相符，说明数值计算结果是准确的。

3.2.3 谐响应分析

对求得的不同工况下叶轮旋转6个周期内径向力随时间变化的函数作快速傅里叶变换，得到频域上的关于径向力的函数。把求得的频域上的函数作为外载荷加载到叶轮结构中心，如图11所示，可以集中表示径向力对叶轮结构的作用，可反映出径向力所产生的结构振动特征。

图11 叶轮谐响应分析设置Fig.11 Impeller harmonic response analysis settings

计算小流量工况0.8Qd、标准工况Qd和大流量工况1.5Qd3种不同工况下的谐响应分析，根据3种不同工况下谐响应分析的计算结果得出了叶轮3种不同工况下的幅频图，如图12所示，从图中可看出，3种不同的工况下频率为101.67 Hz时幅值都比较大，此频率即为叶轮的基频处，表明叶轮所受振动与叶轮的转动有着紧密的联系，在3种不同的工况频率为610 Hz时也都出现了一个明显的峰值，即存在一个频率为610 Hz的正弦分量，此频率和离心泵的叶片通过频率相等，由此说明叶片和隔舌的相互作用对叶轮的振动影响较为明显。

通过图12对比不同工况下叶轮幅值大小，在设计工况Qd时，叶轮结构振动幅值都最小，在小流量工况0.8Qd和大流量工况1.5Qd时，叶轮结构振动幅值比较大，且在大流量工况1.5Qd时振动幅值最大，表明了离心泵工作处于额定流量下振动幅值最小，偏离额定流量越大，振动幅值越大。