高速螺旋密封临界密封能力的结构敏感参数分析
2022-08-25陈潇竹李双喜陈坤毅宋子锋
郑 娆,陈潇竹,李双喜,陈坤毅,宋子锋
(1.北京化工大学 机电工程学院,北京 100029;2.中国船舶工业系统工程研究院,北京 100036)
0 引言
由于螺旋密封具有结构形式简单、密封元件之间有较大间隙,使其静子和转子不会发生碰摩现象且在苛刻条件工况如高温、腐蚀流体、含颗粒流体仍能保持较好密封能力的特点,非常适用于恶劣工况,且具有较好的应用前景。由于螺旋密封在设计时涉及的结构参数众多且参数之间相互耦合,需要分辨出其中影响密封能力较大的结构敏感参数以降低设计难度。这些结构敏感参数与其他参数相比对密封的正常运转和密封性能影响更大,且参数变化影响密封的性能非单调增加或减小。因此需要一种新的优化设计方法满足对螺旋密封结构敏感参数的多参数优化,简便准确地提高螺旋密封的密封能力。
为研究螺旋密封的最大密封能力,刘杰[1]通过对高压工况下的螺旋密封的几何结构的优化设计,证明当螺旋密封长度大于100 mm时螺旋密封可以应用于变压力工况中的设备中。孙卫平等[2]将普通螺旋密封改进为组合式螺旋密封有效地改善了螺旋密封的“气吞”现象。马润梅[3]将螺旋密封视为轴向齿寸较长的轴流泵合理的解释了螺旋密封的工作机理以及“气吞”和“密封失效”的现象。黎义斌等[4]将摩擦因素作为螺旋密封性能的量纲一评价因子,获得了螺旋密封工作参数的选取范围和相互关系。高远等[5]利用CFD软件对类迷宫螺旋密封与迷宫密封的性能进行对比研究,证明了采用类迷宫螺旋密封的可行性。薄相峰等[6]自主设计了螺旋密封试验装置,通过试验分析得出了各参数对螺旋密封性能的影响情况。任朝晖等[7]利用CFD分析了层流运动时螺旋密封在压差力作用下密封介质受力分布和压差力作用下密封介质的速度分布并对螺旋密封结构的参数进行了参数优化。常晓萍等[8]利用蚁群算法对螺旋密封进行了优化设计,仿真结果表明蚁群算法应用于螺旋密封的优化设计是可行的。YANKOV等[9-11]研究了以非牛顿流体为密封介质的螺旋密封封液性能力,以幂律流体二维定常流动速度分布方程替代牛顿流体二维定常流动速度分布方程,近似解析得到密封介质为幂律流体的螺旋密封封液能力表达式。结果表明,当螺旋密封用于密封幂律流体时,封液能力随稠度系数、流性指数、转速的增加而增大;随螺旋角、相对槽宽、相对槽深的增加先增大再减小。
前人对螺旋密封的研究主要为理论推导以及结构设计,对螺旋密封结构敏感参数探究以及对结构敏感参数的优化方法的建立还较少。本文在前人的基础上,从螺旋密封性能出发,利用数值模拟计算方法,找出螺旋密封的结构敏感参数,设计螺旋密封试验对临界密封能力公式进行修正;揭示螺旋密封在各结构敏感参数变化下密封性能变化规律,同时提出了一种优化方法满足螺旋密封敏感参数的多参数优化并准确地提高螺旋密封的临界密封能力。
1 结构与原理
1.1 密封结构
螺旋密封的密封结构如图1所示,本文使用的螺旋密封是在轴的表面切削出矩形螺旋槽,在轴高速旋转的过程中通过产生泵送效应使得密封介质出现反输现象。
1.2 螺旋密封的密封机理
螺旋密封的工作原理借鉴了开槽止推轴承的方法和理论,轴旋转时,螺旋槽将产生逆压差的轴向力,介质在轴向力的作用下,形成一个反向流,平衡密封两端的压力差,使工作介质不发生泄漏。
螺旋密封内部的流动主要分为3种[6]:(1)泵送流量Q1,该流动是由于螺旋轴的旋转使流体在黏性剪切力的作用下的反输送流动,是阻止流体由于压差产生泄漏的流动;(2)沿螺旋槽泄漏流量Q2,该流动是由于压差使得流体沿螺旋槽内泄漏的流量,与泵送流动的方向相反;(3)越螺旋槽泄漏流量Q3,该流动是由于压差使得流体越过螺旋槽泄漏的流量,与泵送流动的方向相反。密封介质的3种流动方式如图1所示。


式中 V ——螺旋轴旋转的线速度,m/s;
D ——螺旋轴的外径,m;
K1——相对槽宽,K1=a/(a+b);
α ——螺旋角,(°);
Δp ——密封压差,MPa;
μ ——被密封介质的黏度,Pa·s;
i ——螺纹头数;
h ——螺纹齿高,m;
s ——齿顶间隙,m;
a ——螺纹槽宽,mm;
L ——螺纹长度,m;
b ——螺纹齿宽,mm。
2 数值模拟
2.1 分析模型
由于螺旋密封流域内存在复杂多变的介质流动,需要建立准确的三维模型以及选择正确的数学模型进行数值计算,运用数值模拟方法能使计算更准确同时能计算流体湍流和气化情况,而螺旋密封经验公式则只能计算流体在层流时密封的泄漏量。
本文的数值模拟计算以螺旋槽的流体域和旋转轴与腔体之间的流体域为研究对象,建立对应的流体域分析模型,如图2所示,其中流体进口处设置压力入口Pin=0.45 MPa(表压),出口处设置压力出口Pout=0 MPa(表压),将流体膜与螺旋面的接触面定义为旋转域并给定旋转速度n=10 000 r/min,与腔体接触面定义为静止域。同时利用ANSYS Workbench中的Mesh模块进行网格划分,经过网格无关化验证,使网格达到了计算精度要求。
图2 流体域边界条件施加情况Fig.2 Application of boundary conditions in fluid domain
螺旋密封的层流和紊流工况由其周向雷诺数Reu判断[12],周向雷诺数计算式见式(4)。周向雷诺数的临界值Reuk计算式见式(5)。当Reu<Reuk时密封中的流体为层流,当Reu>Reuk时密封中的流体为紊流。将参数代入计算Reu=2 948,Reuk=1 697.43,因此在转速n=10 000 r/min时密封中的流体为紊流状态。且根据计算当转速n<5 758 r/min时模型选用层流模型进行计算,当转速n>5 758 r/min时模型选用Standard k-ε的湍流模型进行计算[13]。
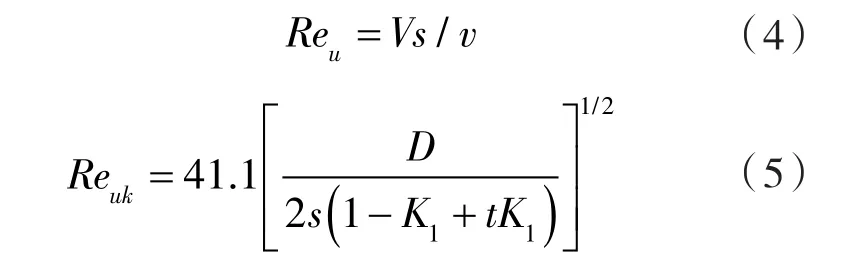
式中 V ——圆周线速度,m/s;
t ——螺旋角正切函数,t=tgα。
2.2 参数设置
螺旋密封的初始结构参数和操作参数见表1,2。
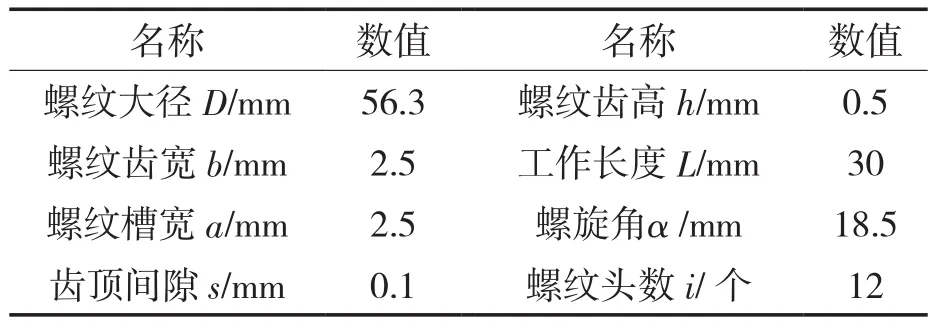
表1 螺旋密封结构参数Tab.1 Structural parameters of spiral seal
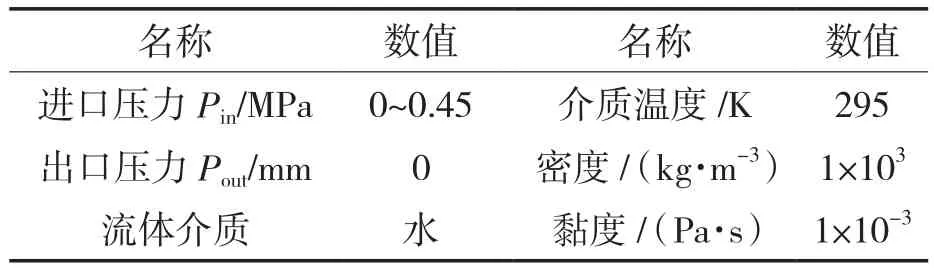
表2 操作参数Tab.2 Operation parameters
2.3 计算结果
通过对流体域施加如图2所示的边界条件,分别分析槽深、相对槽宽对螺旋密封性能的影响。由于螺旋密封在低压高转速工况下会出现流体反向输送的情况,在实际情况下此时泄漏量为零,为了更好地体现出螺旋密封的密封能力,在数值模拟计算时假设螺旋密封低压区存在介质可供密封反向泵送,同时用压力出口流量代替实际泄漏量作为标准来比较结构参数对密封能力的影响。
数值计算得到的流体域压力云图如图3所示,由图3可以看出,流体压力在螺旋流体域逐渐降低,螺旋槽在高速旋转产生的动压效应以及楔形间隙内产生流体动压效应。图4示出螺旋槽流体速度分布,计算得到流体中最大流速v=59.062 m/s,采用最大雷诺数的流体区域判断流态。由图可知,在流场中同时具有沿螺旋槽泄漏部分和越螺旋槽泄漏部分以及密封高速运转产生的泵送部分,该泵送部分阻止了介质的泄漏。

图3 流体域压力分布Fig.3 Fluid distribution in pressure domain
图4 螺旋槽流体域速度分布Fig.4 Velocity distribution in spiral groove fluid domain
2.4 试验装置
为对数值模拟的正确性进行验证,设计试验装置,搭建试验系统,进行变压力、变转速试验。测试不同压力、转速下的螺旋密封泄漏量,与数值计算结果进行对比验证,密封试验装置如图5所示。介质泄漏采用流量计测量,测量密封的出口流量。
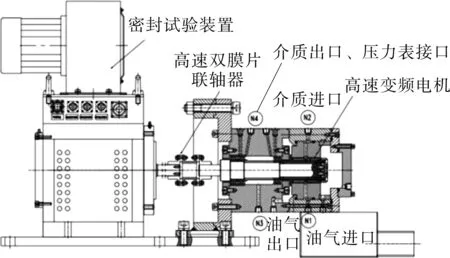
图5 螺旋密封试验装置结构Fig.5 Structure diagram of spiral seal test device
3 结构敏感参数分析
将数值模拟计算结果与试验结果进行对比验证,分析影响螺旋密封的敏感结构参数以及对应泄漏量的变化规律。
3.1 齿顶间隙
由图6可知,泄漏量对齿顶间隙的变化敏感,随齿顶间隙的增加而急剧加大,这是因为根据环形槽泄漏公式可知,泄漏量与间隙的三次方呈反比。从理论上讲密封的齿顶间隙越小越好,但在实际的工程应用中齿顶间隙的大小往往受零件加工精度和密封组件结构的影响更大,过小的齿顶间隙可能导致密封安装困难。综合上述原因,螺旋密封在实际设计中齿顶间隙不应作为结构敏感参数,齿顶间隙应由密封结构和加工精度为依据进行设计,根据试验经验齿顶间隙应选择0.05 mm为宜。
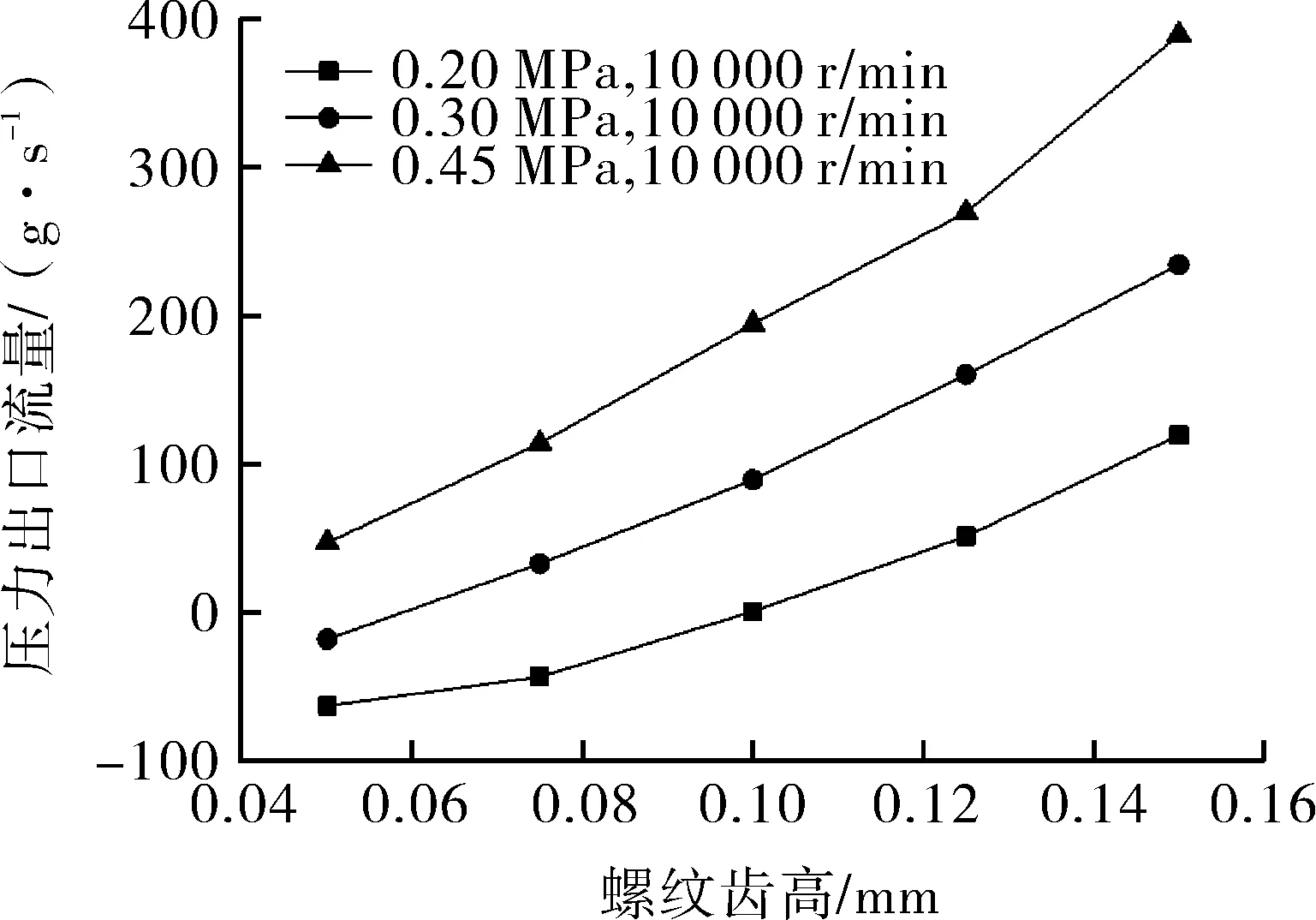
图6 齿顶间隙对泄漏量的影响Fig.6 Influence of tooth tip clearance on leakage
3.2 螺纹齿高
通过数值分析,探究螺纹齿高在0.2~0.8 mm条件下的密封性能。如图7所示,3种工况下密封能力变化规律相同,都是随螺纹齿高的增大先快速增加后逐渐减小。在螺纹齿高增大早期,密封能力对其变化较敏感,密封能力的提升较快,螺纹齿高增大后期,密封能力降低较缓。在螺纹齿高为0.45 mm附近时,密封能力有最大值。螺旋密封的密封能力受螺纹齿高的非线性影响的原因为:螺纹齿高较小时,对应的螺旋槽深也较小,密封由于旋转产生的动压效应也较弱,密封泄漏量大;螺纹齿高增大时,密封产生的动压效应逐渐增强,泵送流量Q1逐渐增大,密封泄漏量逐渐减小;螺纹齿高继续增大时,沿螺旋槽泄漏流量Q2过大此时导致密封泄漏量逐渐增大。
图7 螺纹齿高对泄漏量的影响Fig.7 Influence of thread tooth height on leakage
由于螺纹齿高对密封能力影响较大且其对密封能力影响为非线性使其该参数在设计中有最优值的原因,笔者认为螺纹齿高为螺旋密封的结构敏感参数之一。
3.3 相对槽宽
为研究相对槽宽对密封能力的影响,笔者选取相对槽宽在0.2~0.8范围进行研究。如图8所示,相对槽宽对螺旋密封的密封能力为明显的非线性影响,相对槽宽在0.2~0.5范围变化时,密封能力呈明显的上升趋势同时密封能力在相对槽宽为0.5时达到最高点而后密封能力随相对槽宽的增加而减小。这是由于相对槽宽过小时意味着螺旋密封的螺纹槽宽过大,沿螺旋槽泄漏流量Q2也会相应增大导致密封的整体密封能力下降;而相对槽宽过小时以为着螺旋密封的螺纹齿宽过大,此时泵送流量Q1会相应减小。因此综合二者的影响因素相对槽宽必有1个中间值使得密封能力最大,此值为0.5。同时综合考虑密封得加工难度和整体结构寿命,选择相对槽宽为0.5时使得螺旋密封的整体性能更为优秀。
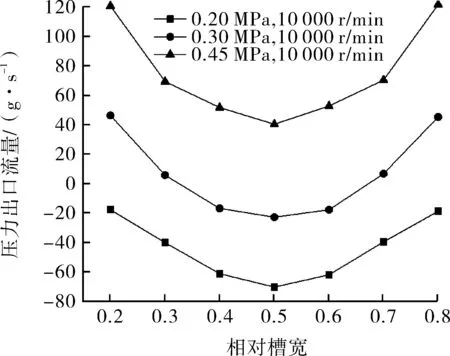
图8 相对槽宽对泄漏量的影响Fig.8 Influence of relative groove width on leakage
由于相对槽宽对密封能力影响较大且其对密封能力影响为非线性使其该参数在设计中有最优值的原因,笔者认为相对槽宽为螺旋密封的结构敏感参数之一。
4 螺旋密封临界密封能力公式参数优化
4.1 临界密封能力公式修正
根据密封内各流量平衡的原理,螺旋密封能完全阻止泄漏即为泵送流量Q1=沿螺旋槽泄漏量Q2+越螺旋槽泄漏量Q3,可以得到螺旋密封的临界密封能力公式,如式(6)所示。
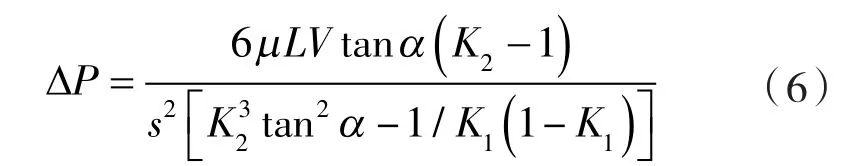
选取7组试验件进行试验,测得不同试验件的密封临界压力值,对比试验值与临界密封能力公式计算所得值,对比情况见表3。
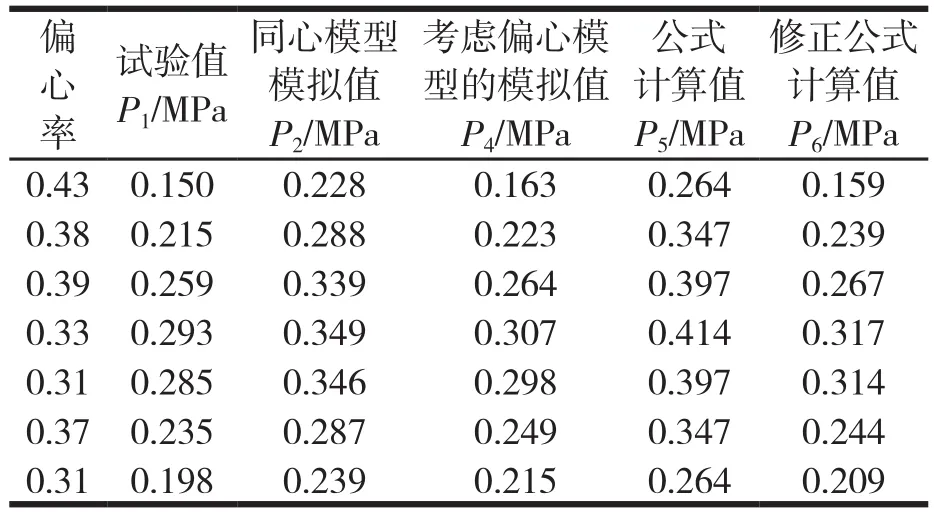
表3 密封临界压力对比Tab.3 Seal Critical Pressure comparison
由表3可知,在相同条件下试验测得的螺旋密封的临界密封压力均小于式(6)计算的临界密封压力,这是因为在制造和安装上的误差,螺旋轴与腔体间会出现偏心情况,而偏心环形间隙内的流体流动中的轴向压力梯度不是定值,而式(6)是在无偏心间隙的基础上推导出来的[14],所以试验值与公式计算值有较大的误差。由于密封的偏心情况的临界密封能力有较大的影响,故引入偏心率对式(6)进行修正,利用电涡流传感器测量了螺旋密封的偏心率。对试验值与公式计算值进行比较,最终利用试验数据进行拟合得到了螺旋密封临界密封能力公式的修正公式见式(7)。
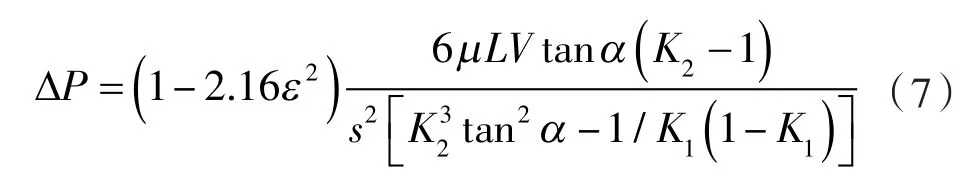
经过临界密封能力公式的修正公式计算得到的值见表3。在数值模拟中同样考虑模型偏心的情况进行计算,利用测得的7组试验件的偏心率同心模型进行修正,计算得到的模拟值见表3。
由表3可知,原临界密封能力公式计算值与模拟值相近但因未考虑螺旋轴与腔体的偏心情况与试验值误差较大,最大误差达到30%。经笔者修正后的临界密封能力公式计算值和考虑偏心影响的数值模拟计算值与试验值相近,最大误差仅为10%。
4.2 优化方法
根据螺旋密封流量平衡的原理得到螺旋密封临界密封能力公式并结合试验结果对公式进行修正。基于修正公式设计了螺旋密封密封能力的优化方法如图9所示。
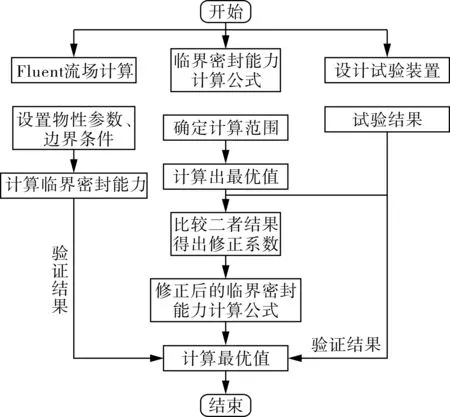
图9 优化流程Fig.9 Optimization flow chart
该方法先对螺旋密封的不同结构参数进行了数值模拟计算,得到了相关结构敏感参数,修正后的临界密封能力公式经过Matlab数值优化后得到了最优的螺旋密封结构参数,最后与数值模拟结果和试验验证证明结果可信。该优化方法能准确得到螺旋密封的最优值,降低了螺旋密封的设计难度。
4.3 优化函数
为了简便准确的通过优化敏感参数从而改进螺旋密封的密封能力,利用fmincon函数对螺旋的封液公式进行数值优化,以找到最优的结构参数[15-18]。
fmincon函数可以求解非线性多元优化方程的最小值。本文中fmincon函数采用SQP算法,该算法具有较快收敛速度、较高计算效率、较强边界搜索能力的特点。
fmincon函数形如:
x=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,option)
4.4 目标函数
目标函数设置为经过修正后的螺旋密封临界密封能力公式(6),提取出公式中的结构参数形成新的函数W如式(7)所示。设x1=α,x2=h,x3=K1,x4=s,由于fmincon函数只能得出目标函数的最小优化值,为了获得函数W的最大值,通过取目标函数W的倒数来实现。所以可以得到目标函数 f(x)如式(8)所示。x1,x2,x3,x4等 4 变量取值范围见式(9)。
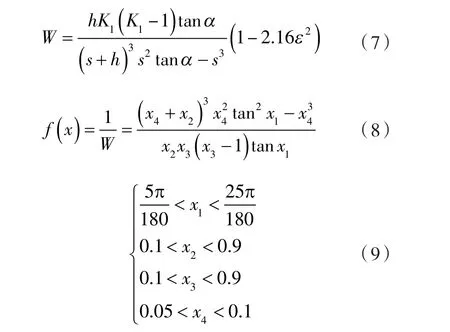
其中,K2为相对槽深,K2=1+h/s。
4.5 优化结果
将目标函数f(x)以及参数的约束条件输入Matlab优化工具箱中,可以得出f(x)的最小值:

同时可以得到函数w在该约束条件下的最大值为:

此时可以得到各参数值:x1=0.323(18.5°),x2=0.45,x3=0.5,x4=0.05
因此,根据fmincon函数的优化,可以得到在螺旋角α=18.5°,螺纹齿高h=0.45 mm,相对槽宽K1=0.5,齿顶间隙s=0.05 mm时螺旋密封具有最优的密封能力。优化后得到的螺纹齿高、相对槽宽、齿顶间隙与模拟值相符,说明优化结果合理。
5 结论
(1)综合考虑对密封能力以及设计制造难易程度,螺旋密封的螺纹齿高和相对槽宽为螺旋密封的结构敏感参数。
(2)对于相对槽宽在0.2~0.8范围内,基于试验结果提出了螺旋密封密封能力公式的修正公式,使其更加复合试验值。
(4)提出了螺旋密封参数的优化方法,该方法结合了数值模拟和Matlab数值优化的方法,准确的对螺旋密封的敏感参数进行了优化,简化了螺旋密封的设计难度。
