基于球谐函数模型的欧洲区域电离层模型
2022-08-25张明泽徐爱功祝会忠徐宗秋唐龙江
张明泽,徐爱功,祝会忠,徐宗秋,唐龙江
(辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)
0 引言
地球上层60 km~2 000 km大气中的分子和原子在太阳的紫外线、X射线和高能粒子的作用下发生电离,形成了等离子体区域,这个区域被称为电离层[1].其中的自由电子和离子是电磁波传播的主要误差源之一,会给导航定位带来延迟误差.电离层延迟一般在几米左右,但当太阳黑子活动强烈时,电离层电子密度会上升,电离层延迟会增大,达到10米甚至几十米[2].因此,削弱和消除电离层延迟对导航定位的影响成为当今全球导航卫星系统(GNSS,Global Navigation Satellite System)领域急需解决的问题[3].电离层的相关科学研究(例如,电离层风暴、电离层闪烁和地磁风暴、地震和海啸的异常变化)需要对电离层状态进行永久和持续的监测.因此,如何最好地获得全球范围内具有高空间和时间分辨率的连续精确电离层模型是精确定位和空间气象应用的热点[4].
各类卫星信号在传播过程中均受到电离层的影响,利用不同频率发射信号延迟不同,可以得到信号传播路径上的总电子含量.根据此特性,国内外众多机构对电离层建模进行了研究.国际GNSS服务(IGS,International GNSS Service)电离层分析中心机构(JPL)利用三角级数电离层模型[5]、欧洲定轨中心(CODE)采用球谐函数模型、UPC采用多层模型建立全球电离层模型[6].2016年,武汉大学和中国科学院大地测量研究所加入了IGS电离层分析中心,并根据自己的创新方法发布了电离层网格产品.与此同时国内外学者也对提高电离层格网产品精度展开充分地研究.文献[7]提供了采用球谐函数模型建立区域电离层的理论依据.文献[8]~文献[10]根据低阶球谐函数模型,采用全球卫星定位系统(GPS,Global Poisioning System)观测数据进行全球、区域电离层建模.文献[11]和文献[12]利用低阶球谐函数模型建立中国区域电离层模型,并对其时空变化特征进行分析.欧洲定轨中心(CODE)每天提供空间分辨率为2.5°×5°,时间分辨率为1 h的全球范围内的电离层格网数据.这些数据被认为是最具有代表性,同时也是最精准的电离层数据.
针对电离层格网选站不均,导致计算结果出现较大误差,基于15阶球谐函数模型,采用2019年第326天至第332天欧洲某地连续运行参考站(CORS, Continuously Operating Reference Stations)网提供的均匀分布的85个测站GPS双频观测数据,建立区域电离层模型,用于取得更高精度的电离层格网,并与CODE提供的全球电离层格网数据进行比较和分析.
1 模型建立
由于电离层是GPS信号的色散介质,因此可以通过与任意两个不同频率的信号形成无几何组合来计算电离层的一阶延迟.根据这一特点,利用载波相位平滑伪距计算电离层TEC的方法提取电离层TEC,即平滑电离层,计算公式为
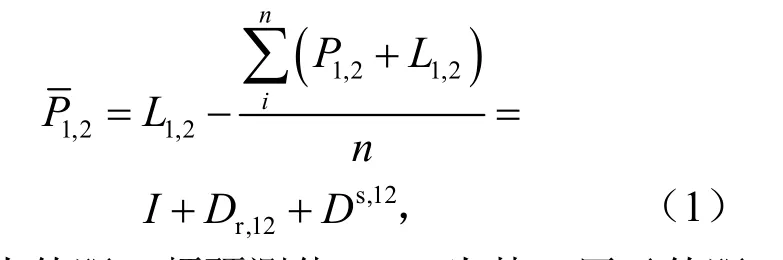
式中,P1,2为伪距双频预测值;L1,2为某一历元伪距双频观测值;P1,2为某一历元载波相位双频观测值;n为平滑历元数;Dr,12为接收机端差分码偏差,Ds,12为卫星端差分码偏差;I为载波相位平滑伪距的电离层延迟观测量.
假如伪距和载波相位观测值不具有相关性,基于载波相位平滑伪距确定的原始电离层中观测信息方差可表示为

常用的电离层投影函数包括余弦函数、klobuchar函数、改进的余弦函数及fanselow函数等,实验采用最简单、最常用的三角投影函数为
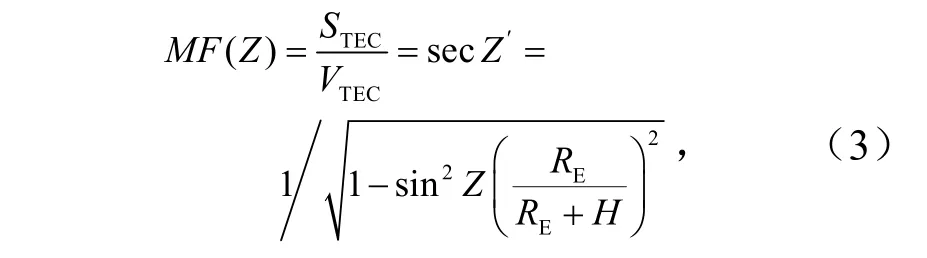
式中,STEC为斜向电离层总电子含量;VTEC为垂直电子总含量;RE为地球的平均半径,km;H为电离层薄层的高度,km;Z和Z′为卫星相对于接收机和IPP处的天顶距,°.
进行区域电离层建模时,实验采用15阶球谐函数模型(SHF,Spherical Harmonic Functions),该模型具有优良的数学结构并能较好地反映总电子含量的时空分布变化.垂直电子总含量球谐函数模型为
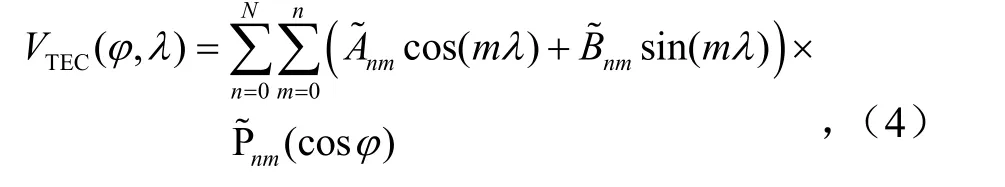
将式(4)代入到式(1)中,可得频间偏差估计模型为
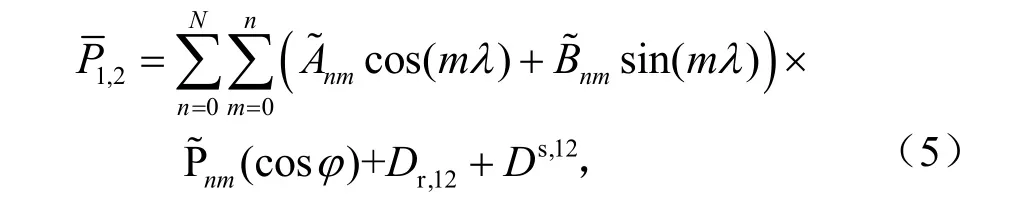
基于最小二乘可处理得到模型系数以及卫星和接收机差分码偏差(DCB,Differential Code Bias)频间偏差参数为
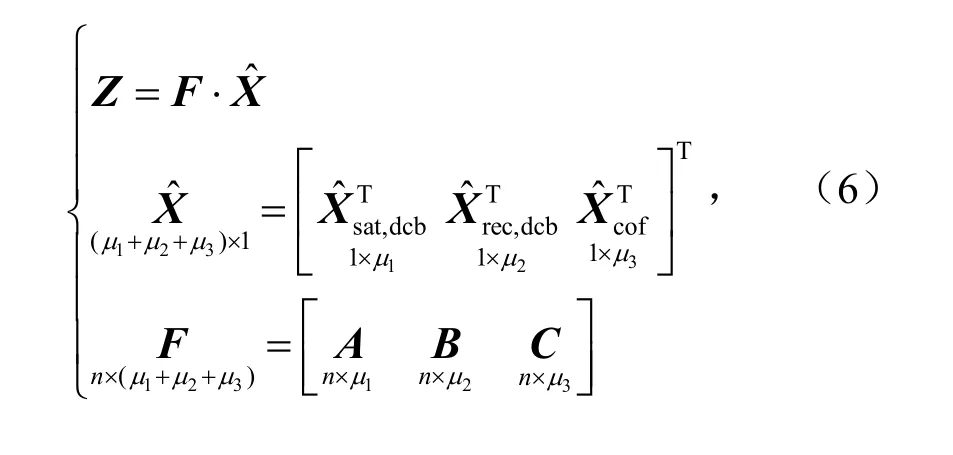
式中,Z为观测卫星频间偏差,以及TEC的模型系数共同组成的列向量;ˆX为未知参数估值,其中分别包括卫星频间偏差,接收机频间偏差以及TEC模型系数;F是分别由矩阵A、矩阵B和矩阵C组成的设计矩阵;μ1、μ2和μ3分别为卫星频间偏差、接收机频间偏差以及TEC模型系数的个数.
勒让德多项式为
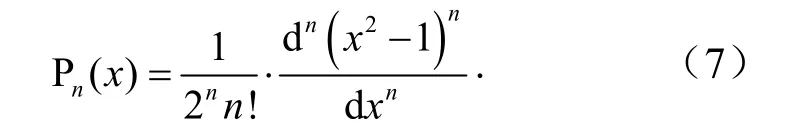
伴随勒让德多项式为
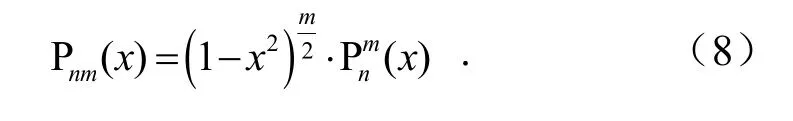
针对一般的球谐函数,为克服低阶次的函数值和高阶次的函数值差别很大的问题,引入一种所谓的“完全正常化球谐函数”,使其不同阶次的完全正常化的球谐函数在数值上差别不大,表示为
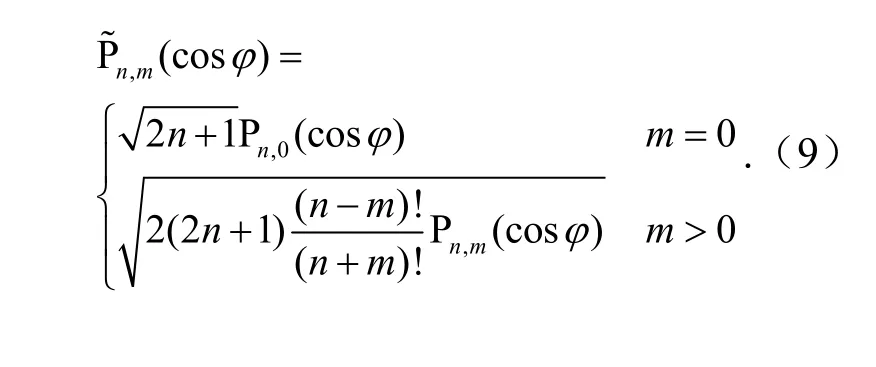
2 数据来源以及实验流程
选取为2019年第326天至第332天的7 d欧洲均匀分布的97个CORS站作为基准站,由于欧洲基准站无法完整的接收到北斗2和北斗3的数据,所以实验采用GPS观测值进行区域电离层建模,测站分布见图1.
图1 欧洲CORS站分布Fig.1 distribution of European CORS stations
观测数据的采样间隔为30 s,卫星截止高度角采用10°,电离层薄层高度选择为450 km,时间分辨率1 h,空间分辨率5°×2.5°,精密星历为IGS提供.本次实验中,欧洲区域电离层建模采用15阶球谐函数模型,按照标准电离层格网的格式进行输出,实验流程见图2.其中,对CORS数据预处理采用国际上公认的GNSS数据预处理软件TEQC,对原始观测数据进行数据格式标准化处理及质量检核分析,剔除观测质量较差的观测文件.
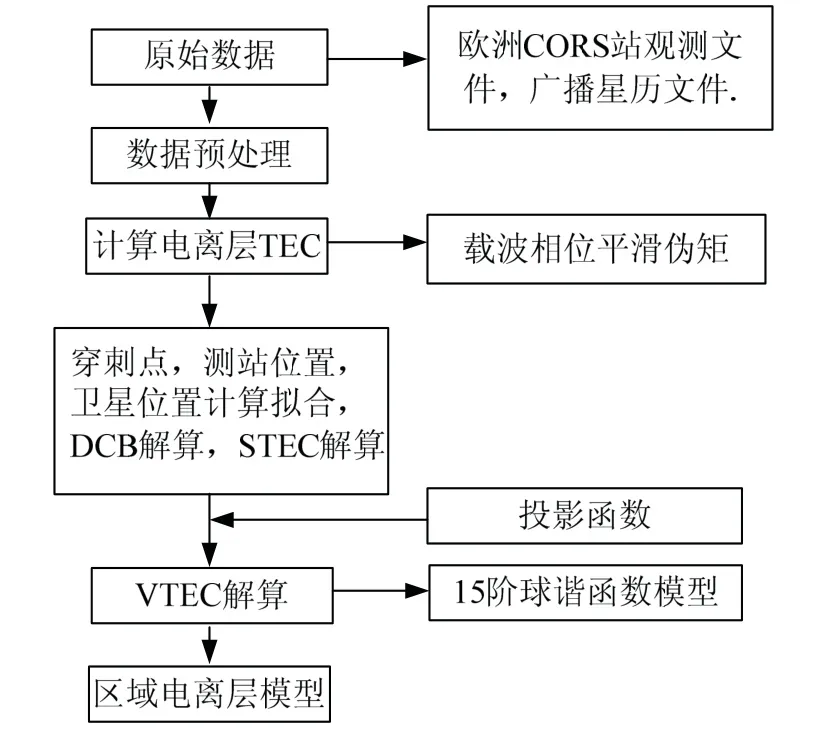
图2 实验流程Fig.2 experimental procedure
3 电离层异常现象及相关指数
指数Kp是衡量中纬度全球地磁活动的指标,取值范围从0至9,共分为28级,指数Kp与磁扰幅度关系为对数函数.在指数Kp的分类上,一般指数Kp取值0~2为平静,2~3为扰动,3~4为活跃,5~6为中小地磁暴,指数Kp达到7~9,称为大地磁暴.
图3为2019年第326天至第332天的指数Kp变化,前3 d的指数Kp相对较大,后4 d的指数Kp相对较小,但均没有发生磁暴现象,总体来说对电离层影响不大.
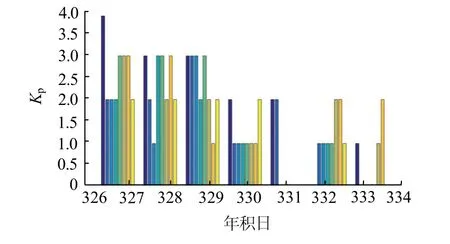
图3 指数Kp变化Fig.3 change of Kp index
图4 为2019年第326天至332天的Dst曲线变化,第327天,地磁暴活动指数(Dst)偏大,但没有达到磁暴程度,这与指数Kp变化趋势一致.
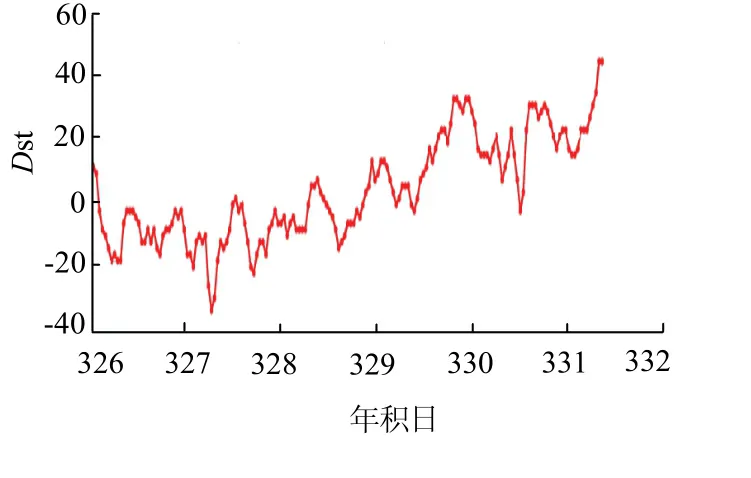
图4 指数Dst变化Fig.4 change of Dst index
4 垂直电子总含量精度分析
对欧洲CORS站的2019年第327天至第332天的GPS双频观测数据进行预处理后,采用载波相位平滑伪距的方法对电离层延迟观测量进行提取,采用最小二乘估计,得到各个时段球谐系数作为模型参数,建立欧洲区域电离层模型,并进行精度评估与可靠性分析.以指数Kp以及指数Dst较差的2019年第327天的数据为例,利用球谐函数模型构建电离层格网VTEC分布,其空间分辨率为5°×2.5°,时间分辨率为2 h,时间为0:00-22:00,横轴为10°E~65°E,纵轴为37.5°N~70°N,时间为当地时间,构建出的图像见图5.
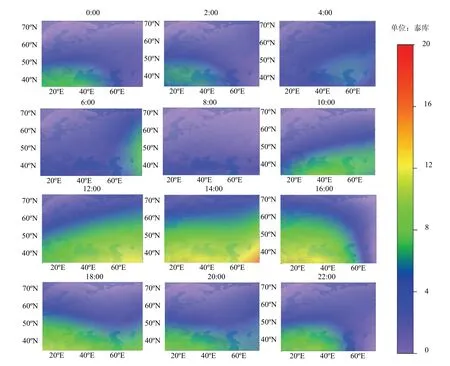
图5 0:00-22:00时区域电离层VTEC分布Fig.5 VTEC distribution of the regional ionosphere at 0:00-22:00
从图5可以看出欧洲区域电离层的时空变化特征较明显.在时间分布上,当位于深夜和凌晨时,电离层较平缓.早上太阳初升时,电离层活动较弱,VTEC较小.随着光照逐渐变强,电离层活动逐渐增强,VTEC逐渐增大,并于光照最强的14:00(当地时间)达到巅峰,之后随着光照减弱,VTEC不断降低.晚上无日照时,电离层较为稳定,VTEC无明显变化.在空间分布上,在欧洲范围内越靠近低纬度地区,VTEC变化程度也就越明显,其变化程度明显高于高纬度地区VTEC变化程度.根据以上分析可知构建出的欧洲区域电离层VTEC格网符合电离层实际时空变化特征.
为验证实验构建的球谐函数模型精度,将计算的第327天欧洲地区电离层格网数据与CODE提供的电离层格网数据作差,结果见图6.VTEC残差基本保持在2泰库(Total Electron Content Unit,简称TECU)之内,残差最大为4 TECU之内.在当地时间的10:00-14:00,电离层处于活跃状态,VTEC差较大,且分布不均匀;当地时间15:00之后,电离层处于平静状态,VTEC残差基本保持在1.5 TECU以内.观察残差分布可知,VTEC残差大的多处于观测站比较少的低纬度地区,这是因为在低纬度地区电离层活动较剧烈,且IGS观测站较少,观测数据不丰富等因素,导致反演的电离层格网精度相对较低.
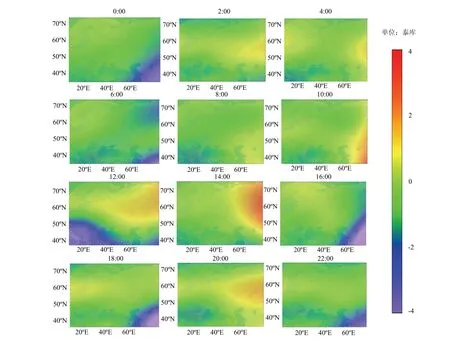
图6 0:00-22:00时区域电离层VTEC残差Fig.6 regional ionospheric VTEC residual at 0:00-22:00
以CODE提供的电离层产品作为参考值,将建立的欧洲区域电离层产品与CODE提供的电离层产品进行比较分析,得到的VTEC差作为评价依据.表3列举出年积日为第326天至第332天的欧洲区域电离层模型与CODE发布全球模型VTEC差统计.
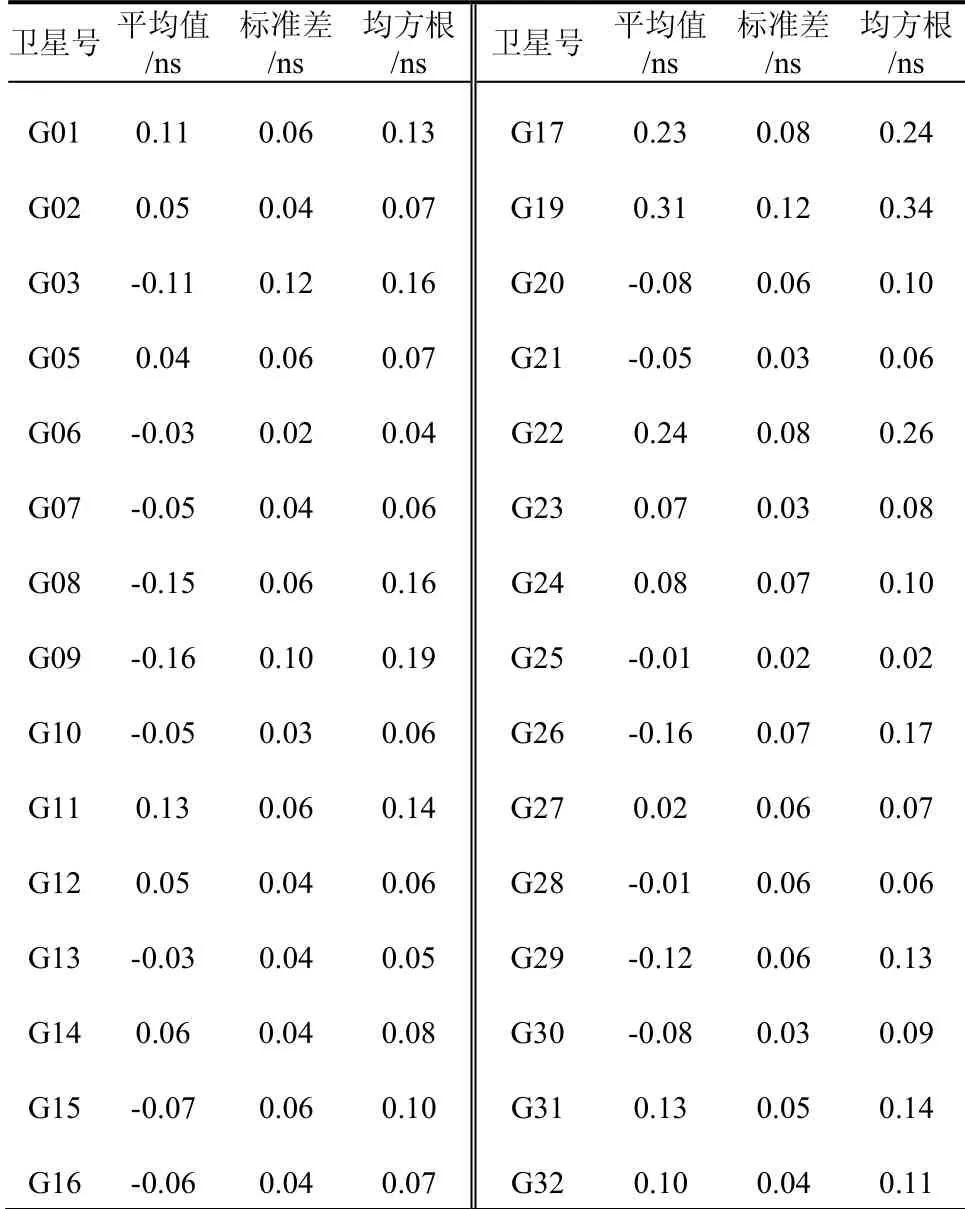
表3 卫星DCB与CODE之差的精度统计Tab.3 accuracy statistics of the difference between satellite DCB and CODE
由表1可知,在第327天差的均方根(RMS,Root Mean Square)和平均值的绝对值达到最大,分别是1.54 TECU和0.65 TECU,第332天值的均方根和平均值的绝对值最小,分别为1.08 TECU和 0.28 TECU.这7 d中的均方根的均值为1.30,标准差的均值为1.26.第327天的均方根最大,与指数Kp和指数Dst在当天有1个小的峰值相对应,表明其对电离层延迟的求解造成一定的影响,但由于指数Kp和指数Dst较小,未达到磁暴水平,所以影响不大.通过表1中数据以及变化趋势可知,采用球谐函数建立的欧洲电离层模型的精度较高.
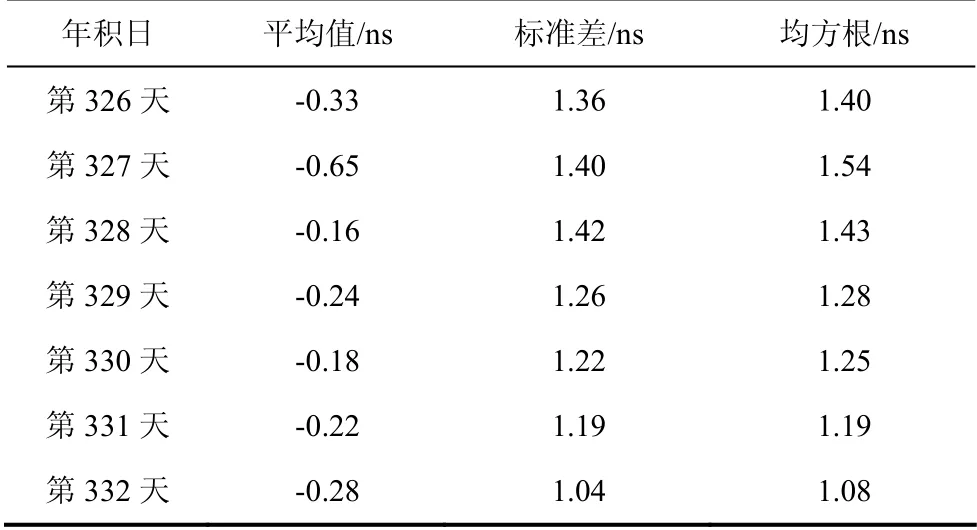
表1 欧洲区域电离层模型与CODE发布全球模型 VTEC差统计Tab.1 difference statistics between the European regional ionosphere model and the CODE published global model VTEC
4 差分码偏差及穿刺点分析
4.1 稳定性分析
对欧洲CORS站的2019年第326天至第332天的GPS双频观测数据进行预处理后,采用载波相位平滑伪距的方法对电离层延迟观测量进行提取,并利用最小二乘求解GPS卫星的DCB.图7为年积日为第326天至332天计算得到的P1、P2频率的DCB频间偏差.表2为GPS卫星DCB的均值以及标准差.从图7中看出第326天至332天的DCB日变化量很小,在0.03 ns以内进行波动.从表2中看出所有GPS卫星DCB的标准差皆优于0.06 ns,证明求解出DCB稳定性高.其中稳定性最高的为G12卫星,标准差达到0.01 ns.
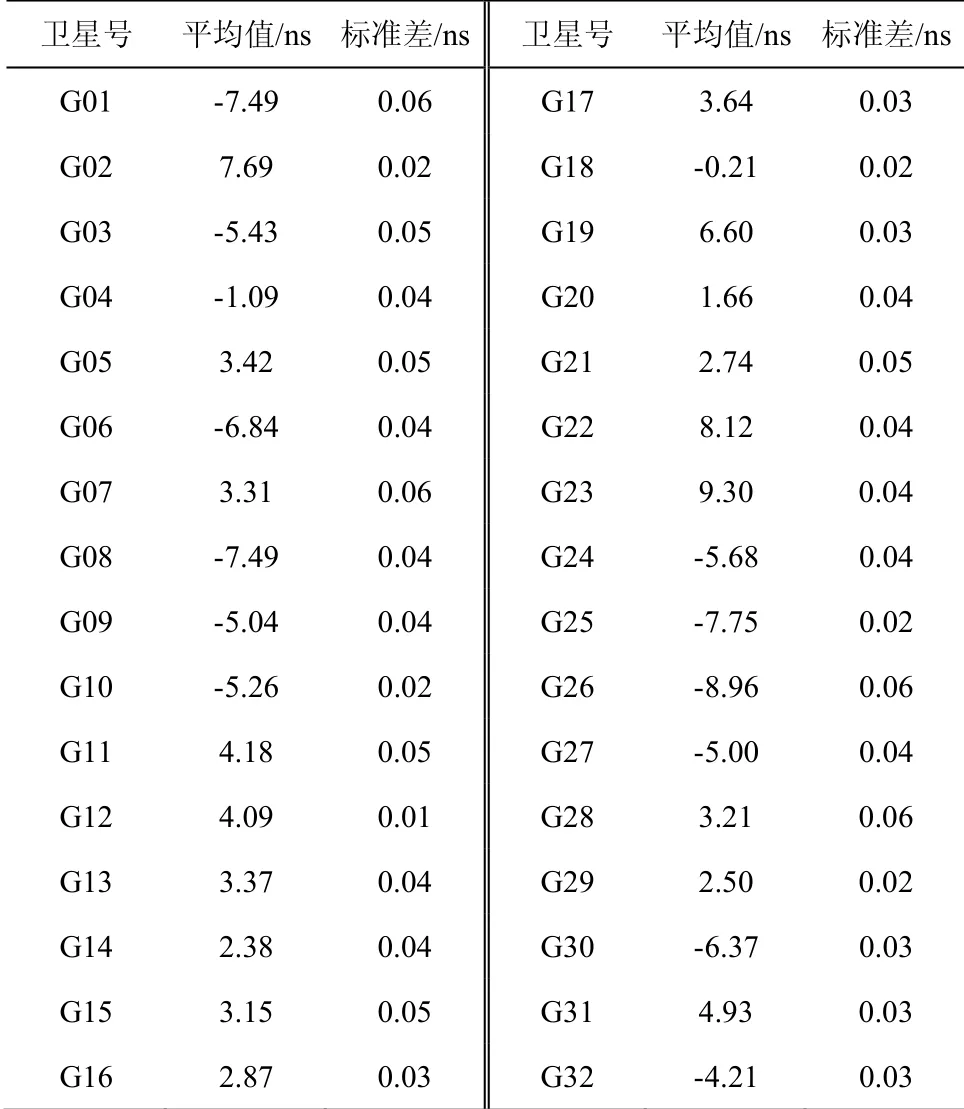
表2 GPS卫星 DCB精度统计Tab.2 accuracy statistics of GPS satellite DCB
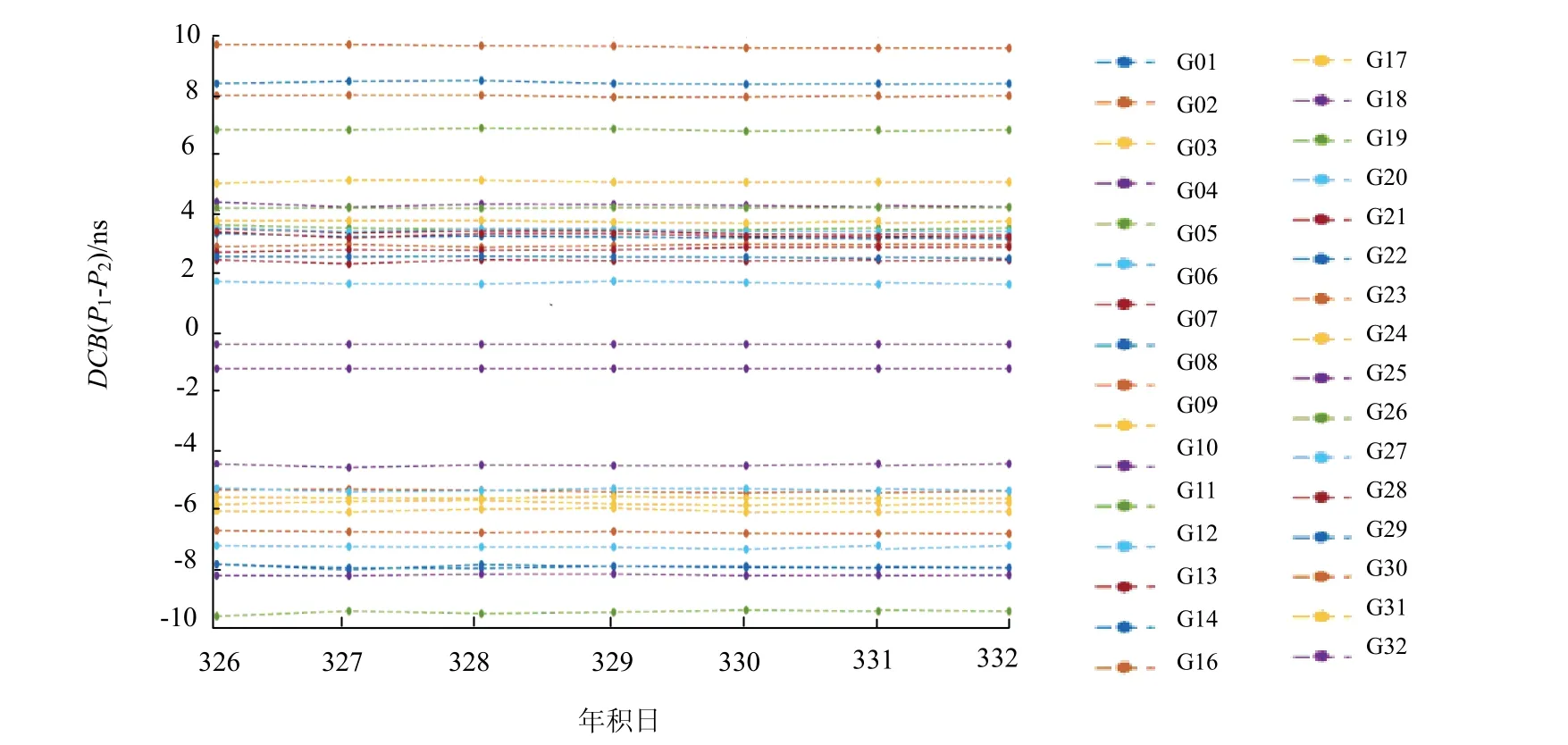
图7 GPS卫星DCB值Fig.7 DCB value of GPS satellite
4.2 可靠性分析
图8显示了年积日为2019年第326天至332天,PRN编号为1~32的GPS卫星DCB估计值与CODE发布值之差的情况.
如图8所示,GPS卫星在所选时段内的DCB与CODE提供的DCB频间偏差数据差值在0.4 ns以内,精度良好.其中的绝大部分能保持在0.3 ns以内,精度较高.

图8 GPS卫星DCB偏差Fig.8 DCB deviation of GPS satellite
由表3可以看出,本计算结果与CODE之差的平均值在0.15 ns以下,标准差保持在0.12 ns以下,RMS在0.2 ns以下,具有较高的稳定性.由图8、表3可以看出,利用欧洲CORS数据建立区域电离层模型解算GPS卫星DCB的稳定性、可靠性较高.
4.3 穿刺点位置分析
以2019年第327天的数据为例,分析了穿刺点的特点.图9显示了2019年11月23日14:00的GPS系统位于欧洲地区的穿刺点(IPP,Ionospheric Pierce Point)分布.GPS系统的IPP分布在欧洲地区较为密集,能覆盖欧洲绝大部分地区,因为欧洲地区有大量跟踪站和一个完整的卫星星座,这为欧洲地区电离层模型的高精度提供了保障.
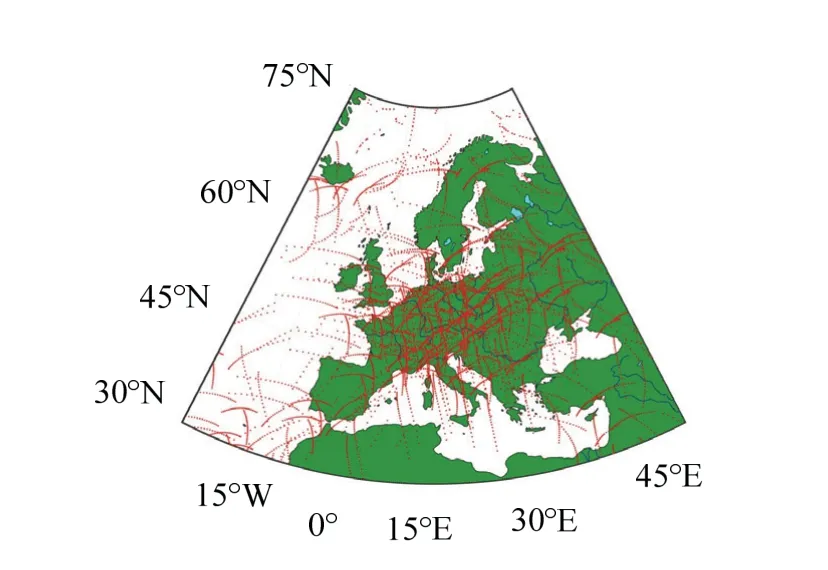
图9 2019年第327天欧洲地区穿刺点分布Fig.9 distribution for point of puncture in Europe at the 327 d of 2019
5 欧洲区域电离层在PPP中应用
为了对建立的欧洲区域电离层模型进行进一步的分析与评估,将欧洲区域电离层模型运用到双频观测值利用非差非组合计算精密单点定位(PPP,Precise Point Positioning)中,并与双频无电离层组合定位结果,以及加入CODE电离层模型的非差非组合计算PPP定位结果进行比较分析,以验证精度.
随机选取6个2019年第327天的欧洲基准站双频观测数据,分别利用双频消电离层组合,加入欧洲区域电离层的双频数据,以及加入CODE电离层的双频数据进行PPP解算.将得到的结果分别与IGS提供的坐标真实值进行比较,残差值绝对值见表4.
从表4可以看出,双频消电离层组合模型E方向、N方向上的精度较高,U方向精度较低.而非差非组合模型在E方向PPP解算精度没有明显提高,N方向稍有改善,但U方向PPP精度有大幅度提高.非差非组合模型定位残差E方向小于0.3 cm、N方向小于0.42 cm、U方向小于0.6 cm,区域电离层模型对U方向精度改善最为明显.在U方向上,加入CODE电离层模型的解算精度稍好于加入欧洲区域电离层模型的解算精度,但总体的解算精度则是加入欧洲电离层模型的更高,提高了0.32 cm.说明加入欧洲区域电离层模型使PPP精度得到进一步提高.统计以上6个测站第326天至332天的PPP定位结果,残差绝对值的平均值结果见表5.
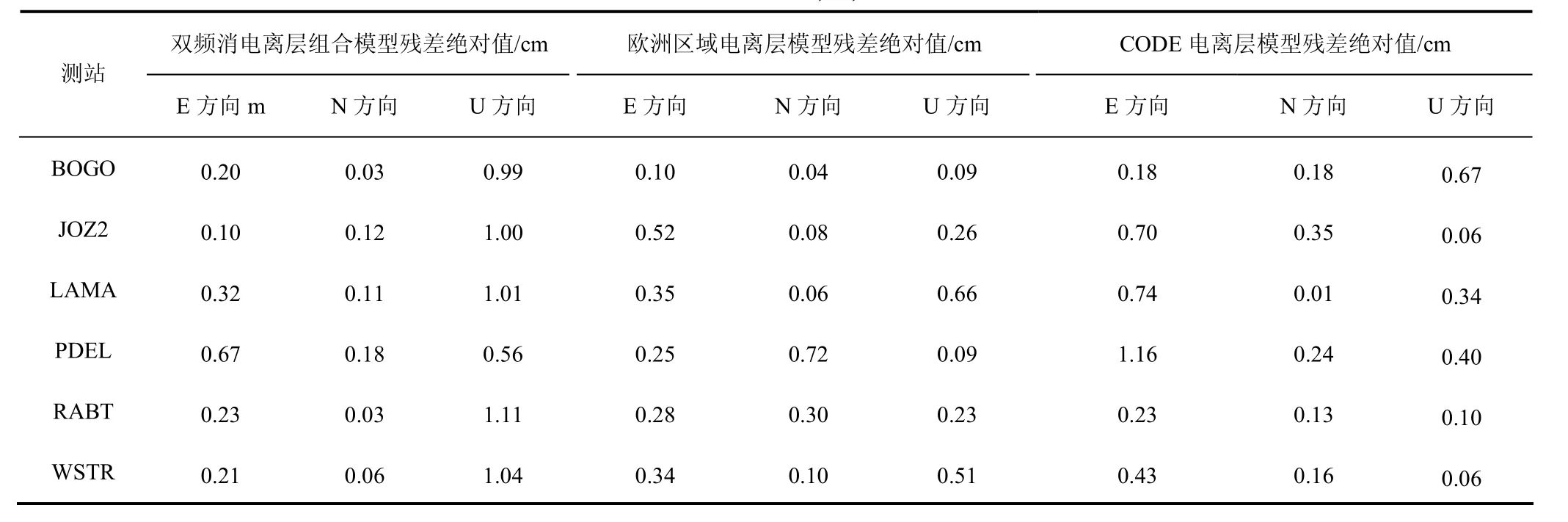
表4 2019年第327天E方向、N方向、U方向残差绝对值Tab.4 absolute value of residual error in the E, N, and U directions at the 327 d of 2019
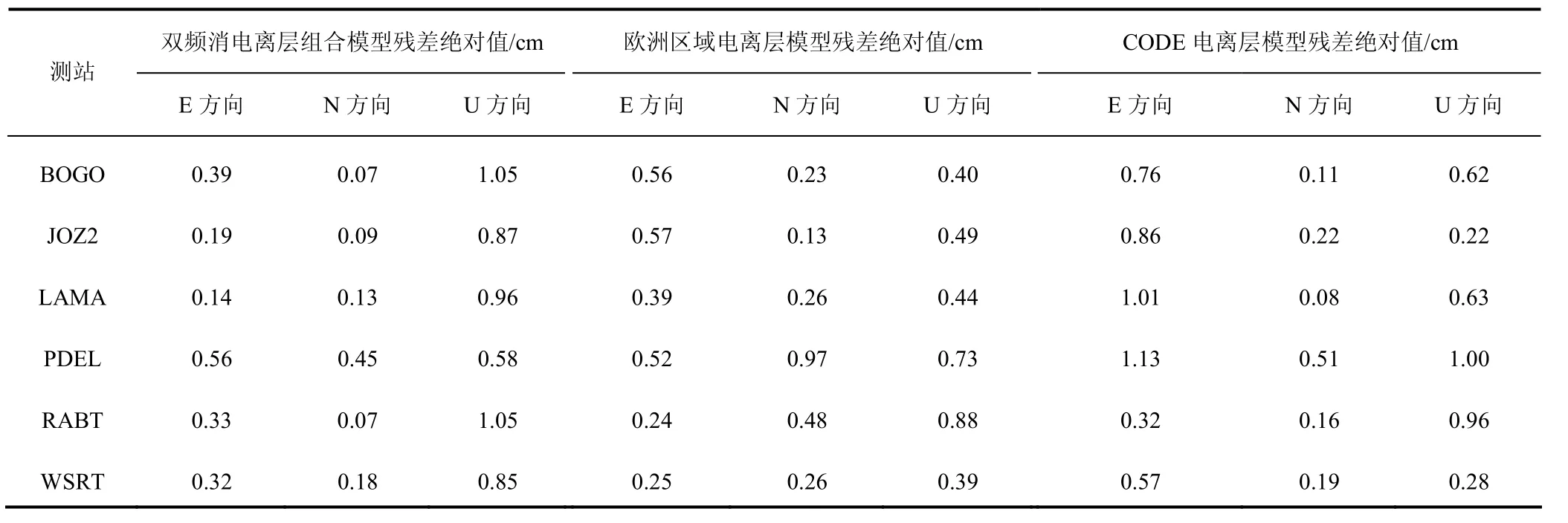
表5 2019年第326天至332天E方向、N方向、U方向残差绝对值Tab.5 absolute value of residual error in the E, N, and U directions at the 326~332 d of 2019
6 结论
借助15阶球谐函数模型,利用欧洲CORS站均匀分布的85个测站的GPS双频观测数据建立欧洲区域电离层模型,并进行可靠性、稳定性分析,最后利用精密单点定位进行合理性验证,得出以下结论.
(1)欧洲区域电离层中GPS卫星的DCB日变化量保持在0.03 ns以下.所有GPS卫星DCB的标准差高于0.06 ns、均方根高于0.07 ns.
(2)通过计算得到的GPS卫星在2019年第326天至第332天的DCB与CODE机构提供的DCB频间偏差数据相比差值始终保持在0.4 ns以下,具有良好的精度.通过模型计算得到的DCB与CODE提供的DCB之差的平均值普遍在0.1 ns以下,均方根普遍在0.2 ns以下.
(3)第327 d加入欧洲电离层模型的双频精密单点,在U方向精度有大幅度提高.第326天至332 天的双频精密单点定位结果显示,加入欧洲电离层模型改正的定位结果在U方向的解算精度得到大幅度提高,并且加入欧洲区域电离层模型的双频PPP解算精度高于加入CODE电离层的双频PPP的解算精度.
