超构表面单元旋转对称性对极化转换的影响

李凤娇，汪剑波，张文琪，张东辉

（长春理工大学 物理学院，长春 130022）

电磁波的极化是指电场强度矢量随时间变化的方式，一般有线极化、圆极化和椭圆极化三种极化方式。对电磁波的极化的调控在军用及民用方面都有很重要的作用，在无线电技术中，电磁波以不同极化方式传播，可以实现无线电技术信号的最佳发射和接收［1］。在通信方面，电磁波的极化可使通信设备的抗干扰能力增强，且提高通信的容量［2-3］。利用极化检测技术可以提高所识别目标的探测能力［4］。传统调控极化的材料主要是双折射晶体和拨片，但这些材料结构尺寸较大，难以满足如今的需求。由于超表面是一种具有独特物理性质的人工电磁材料，能实现自然材料无法实现的奇异特性，如负介电常数和负磁导率等［5］。故使用超表面对电磁波极化进行调控成为一种新的思路。

目前对极化转换器的研究倾向于提高转换效率和增加带宽［6-7］，例如 Nathaniel K G 等人［8］设计了简单的偶极子交叉极化转换超材料，在0.8～1.8 THz范围内反射型结构的极化转换效率达80%；徐进等人［9］设计了一款方形开口环线极化转换器，在7.12～18.82 GHz超宽带内交叉极化转换效率高于90%；Lévesque Q等人［10］设计了一款L形天线，在红外波范围内的线极化转换效率达95%。这些交叉极化转器大多为二重旋转对称结构，且都倾向于提高极化转换的效率及带宽，很少有多重旋转对称性对极化转换性能方面的研究，因此，设计一款“一字”形极化转换器，分析极化转换器表面结构的不同旋转对称对交叉极化转换性能的影响。

1 理论分析

通过分析电磁波在三层超表面结构中的反射和透射来分析极化转换特性［11］，如图1所示。由于极化转换超表面的结构具有各向异性，故反射波和透射波均会形成交叉极化波和同极化波。

图1 电磁波在三层介质中的反射与透射过程

当y极化电磁波入射到超表面，此时产生的反 射 系 数 分 别 为产 生 透 射 系 数 分 别 为透射进介质中的电磁波在金属板处被完全反射后再次在超表面进行反射和透射，此时 产 生 的 反 射 系 数 分 别 为产生的透射 系 数 分 别 为每次的反射系数与透射系数均包含相应的幅值和相位（如的幅值是rxy12，相位是φxy12），电磁波在中间介质层中的传输相位，金属板的反射系数=-1。因此，当y极化波入射时，可以通过叠加所有多次反射，得到最终的交叉极化反射系数：

如果第一次的同极化反射系数与后面多次的同极化反射系数出现了干涉相消，则产生极化转换的概率会很小甚至没有，即ryy=0，此时便能实现极化转换。

2 模型设计及仿真

2.1 模型设计及仿真

基于上述分析，设计了“一字”形交叉极化转换器，如图2所示。极化转换器由“一字”形金属表面、二氧化硅介质与金属底板组成。单元结构的周期p=210 nm，顶层的超表面和底层金属选用理想电导体PEC，厚度均为1 nm，“一字”形的长度l=150 nm，宽度w=40 nm。二氧化硅介质层的相对介电常数为3.9，厚度t=60 nm。在可见光波段内，该结构可实现高效和宽频带的极化转换。

图2 极化转换单元结构图

基于时域有限差分法仿真计算此极化转换器的交叉极化反射系数rxy(ryx)和同极化反射系数ryy(rxx)。电场沿y轴的线极化波入射，设置边界条件为周期边界条件。经仿真得到交叉极化反射系数rxy和同极化反射系数ryy，如图3（a）所示，在476.2～739.5 THz频段内，交叉极化反射系数rxy接近于1，由此说明，入射的线极化波经过超表面反射后转化成了与其垂直的线极化波。根据求得的交叉极化反射系数rxy和同极化反射系数ryy可得到极化转换器的PCR，如图3（b）所示，由图可以看出，在438.1～768.1 THz频段内，其极化转换效率高于90%；在424.3～781.3 THz频段内，其极化转换效率高于80%，带宽为357 THz。由此说明，所设计的超表面可以在宽的频率范围内实现高效的极化转换。

图3 仿真结果

2.2 物理机理分析

为了揭示超表面实现极化转换的物理机理，首先对入射的电磁波进行正交分解，如图4（a）所示，入射电磁波电场在y方向，电场为Ei，将其分解成u和v方向的两个分量，电场分别为Eiu和Eiv，u轴和v轴分别沿着“一字”贴片的长轴和短轴方向，反射电场在u轴和v轴上的电场分量分别为Eru和Erv，相应反射系数分别为和͂，反射系数的相位差为Δφ。当ru=rv=1，且Δφ=180°时，电磁波能由y极化转变为x极化。通过仿真设置入射波的极化方向，得到沿u轴和沿v轴反射系数的幅值和相位，如图4（b）所示。由图可知，在438.1～768.1 THz频率范围内，反射系数和的幅值ru和rv基本一致，趋近于 1，相位差Δφ基本趋近180°。

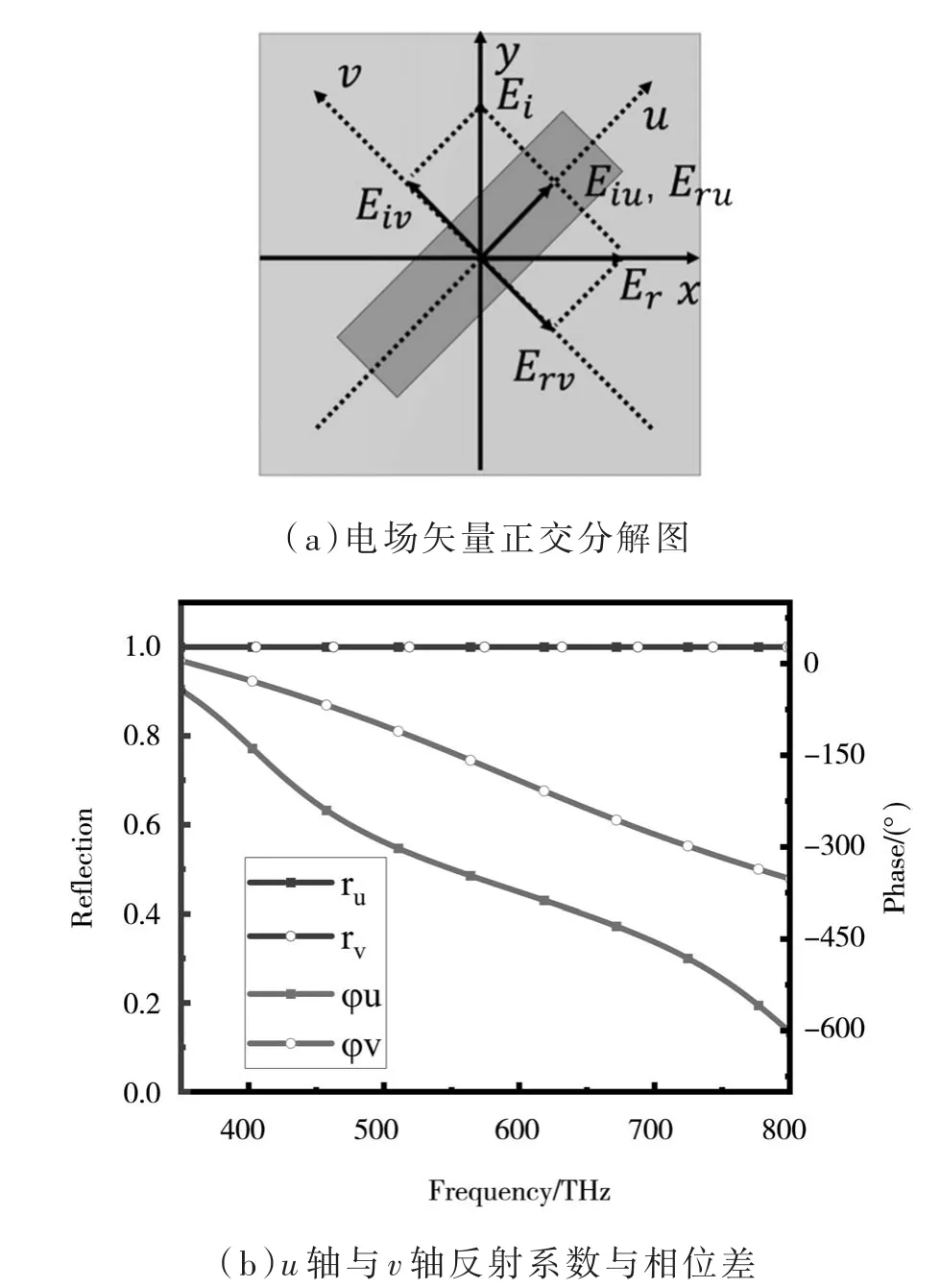
图4 电场分解及仿真结果

为了对该极化转换器的工作机理进行进一步的研究，基于时域有限差分法对该结构的表面电流进行了仿真，上下两层理想电导体在谐振频段490.9 THz、589.9 THz和718 THz处的电流分布如图5所示。为了清晰地显示电流流向，用黑色箭头对电流的方向进行标注。由图5（a）和图5（b）可以看出，在490.9 THz和589.9 THz处，顶层和底层的电流流向均相反，此时该极化转换器表现出磁偶极子特性，从而产生磁谐振，形成了感应磁场H1和H2，由于感应磁场H1和H2在y方向的分量H1y和H2y与入射电场Ei平行，从而产生交叉耦合，导致交叉极化的产生，最终使得y方向电场向x方向转换。在718 THz处，如图5（c）所示，顶层电流的流向主要为斜向上，底层的电流流向与顶层的流向基本相同，此时该极化转换器表现出电偶极子特性，从而形成了感应电场E3，感应电场E3沿x方向的分量E3x垂直于入射电场Ei，从而产生交叉耦合，从而导致极化转换的产生。490.9 THz处主要是上层贴片的长轴与底层贴片耦合，589.9 THz处主要是上层贴片的短轴与底层贴片耦合，718 THz处主要是单元间的响应。

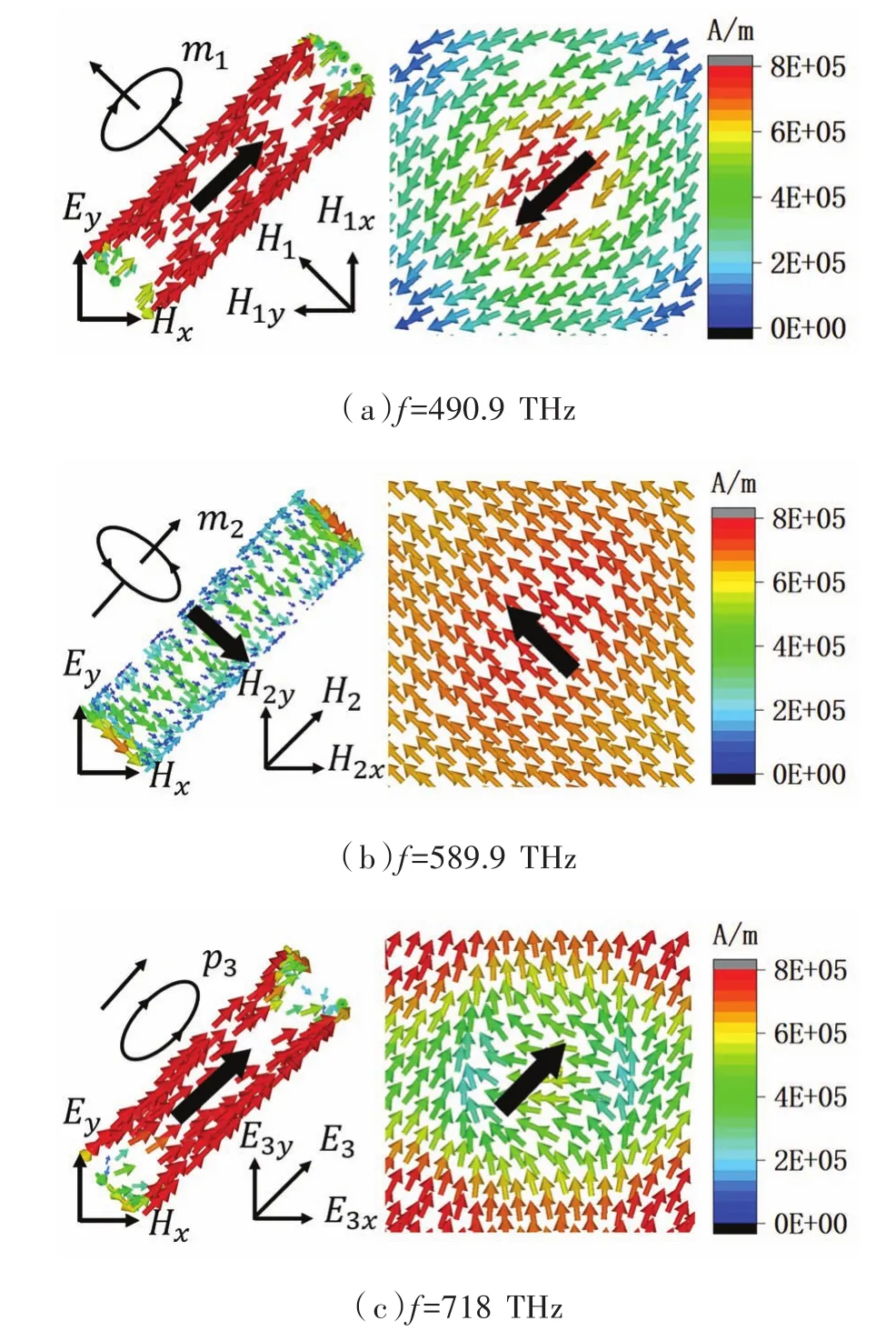
图5 不同频点下表层和底层电流分布

3 偶极子旋转对称性对传输特性的影响

为了研究偶极子旋转对称对极化转换特性的影响，故对上述结构的表面进行旋转，分析其多重旋转对称对交叉极化转换的影响。不同旋转单元所使用的材料与上述“一字”单元结构所使用的材料相同，超表面和底层金属板的厚度不变，均为1 nm。不同旋转对称单元结构如图6所示。图6（a）为二重旋转对称结构，其仿真结果如图3所示。由于四重旋转对称单元在u轴和v轴方向不具有各向异性，故不做研究。下面分别对三重旋转对称结构、五重旋转对称结构和六重旋转对称结构进行分析。

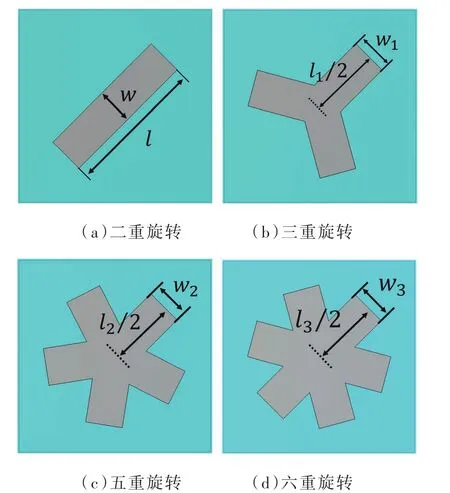
图6 不同旋转对称单元表面结构图

3.1 三重旋转对称

设计“一字”单元的三重旋转对称单元，其单元结构如图6（b）所示。单元结构的材料与上述单元相同，周期p=210 nm，结构参数l1=150 nm，w1=40 nm，介质层厚度t1=104 nm。通过时域有限差分法对其仿真，电场沿y轴的线极化波入射，设置边界条件为周期边界条件，得到反射系数，如图 7（a）所示，由图 7（a）可以看出，在651～657 THz频率范围内，交叉极化反射系数rxy大于0.9，同极化反射系数ryy小于0.45。极化转换效率如图 7（b）所示，由图 7（b）可以看出，极化转换效率高于80%时，带宽为6 THz。

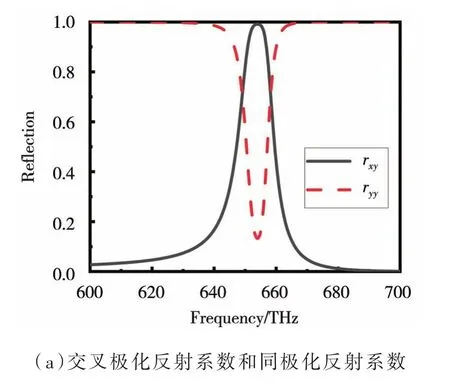
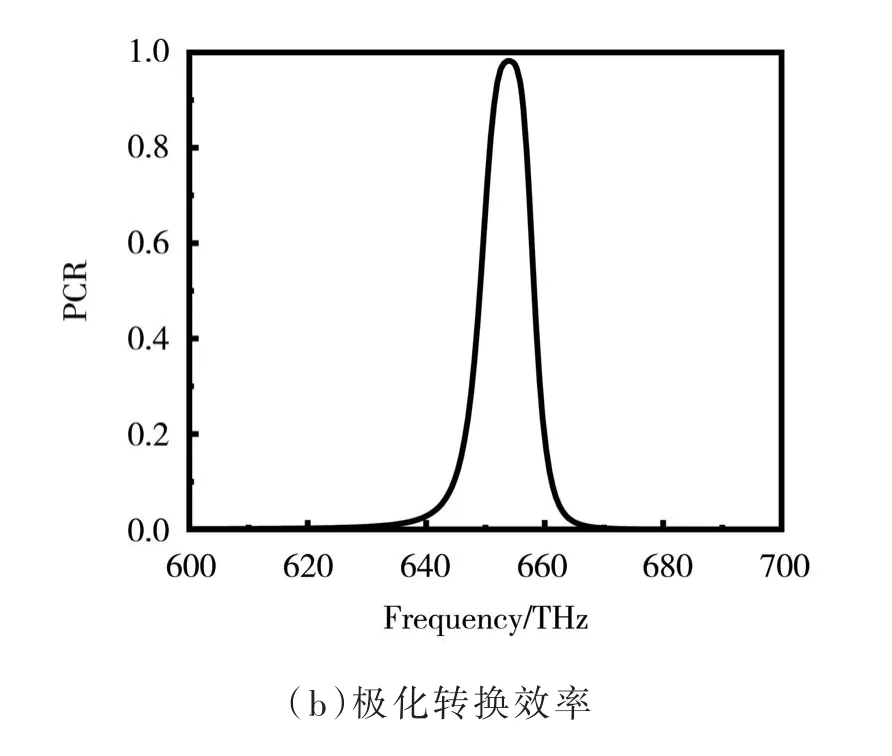
图7 三重旋转对称单元仿真结果

对谐振频点654.2 THz处的表面电流进行仿真，仿真结果如图8所示。从图中可以看出，在654.2 THz谐振频点处，顶层和底层的电流流向相同，产生电共振，形成斜向右上方的感应电场，感应电场沿x方向的分量Ex垂直于入射电场Ei，Ex和Ei之间存在交叉耦合，从而有助于极化转换。

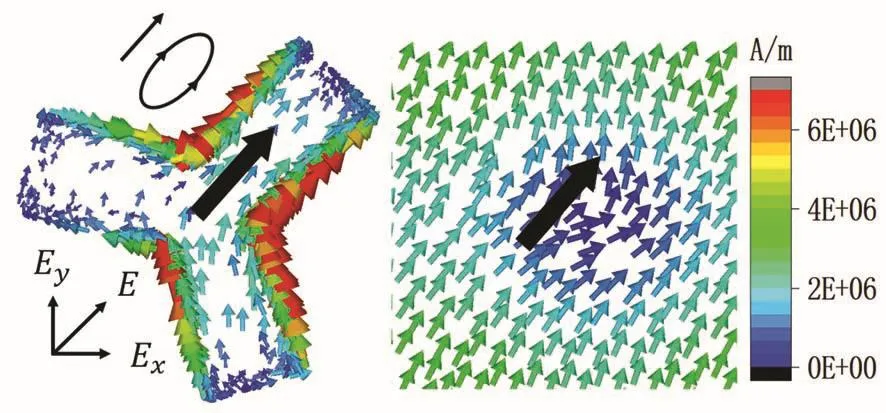
图8 三重旋转对称结构在谐振频点654.2 THz处顶层和底层电流分布

3.2 五重旋转对称

五重旋转对称单元的单元结构如图6（c）所示。单元结构的材料与“一字”单元相同，周期p2=210 nm，结构参数l2=150 nm，w2=40 nm，介质层厚度t2=106 nm。通过仿真，得到反射系数rxy和ryy，如图 9（a）所示，由图 9（a）可以看出，在680.8～681.7 THz频率范围内，交叉极化反射系数rxy大于0.85，同极化反射系数ryy小于0.50。极化转换效率如图9（b）所示。由图9（b）可以看出，极化转换效率高于80%时，带宽为0.9 THz。

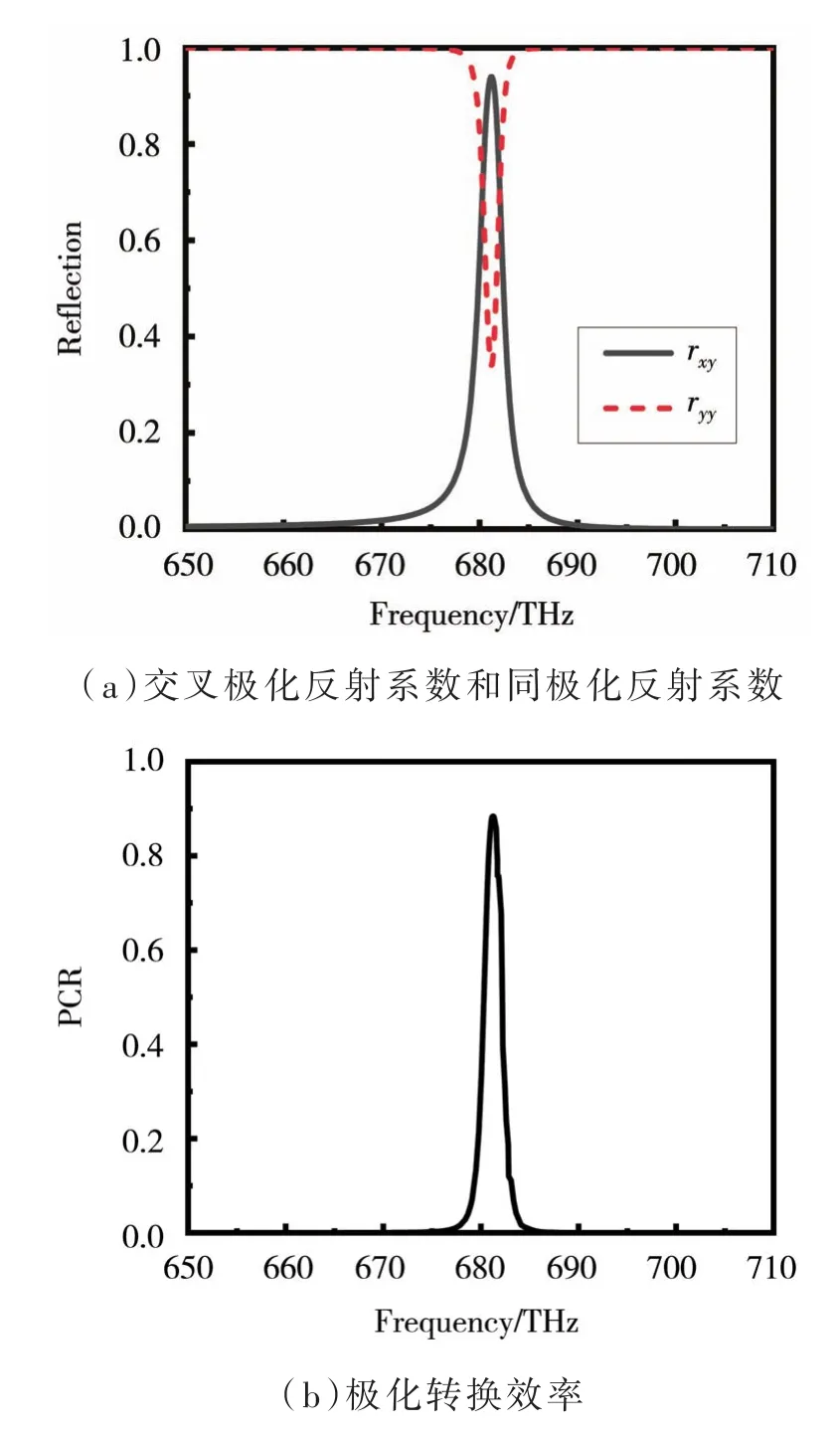
图9 五重旋转对称单元仿真结果

对谐振频点681.3 THz处的表面电流进行仿真，仿真结果如图10所示。从图中可以看出，在681.3 THz谐振频点处，顶层和底层的电流流向相同，产生电共振，形成斜向右上方的感应电场，感应电场沿x方向的分量Ex垂直于入射电场Ei，Ex和Ei之间存在交叉耦合，从而有助于极化转换。

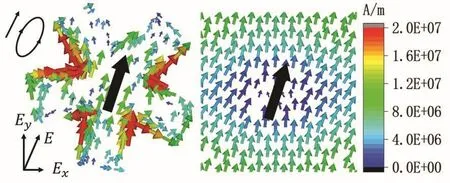
图10 五重旋转对称结构在谐振频点681.3 THz处顶层和底层电流分布

3.3 六重旋转对称

六重旋转对称单元的单元结构如图6（d）所示。单元结构的材料与“一字”单元相同，周期p3=245 nm，结构参数l3=150 nm，w3=40 nm，介质层厚度t3=112 nm。通过仿真得到反射系数rxy和ryy，如图 11（a）所示，由图 11（a）可以看出，在710～730 THz的范围内，出现了两个谐振频点，分别在718.59 THz处和722.64 THz处。极化转换效率如图 11（b）所示。由图 11（b）可以看出，极化转换效率高于80%的带宽分别为0.3 THz（718.4～718.7 THz）和 0.5 THz（722.4～722.9 THz），带宽分别为0.3 THz和0.5 THz。

图11 六重旋转对称单元仿真结果

分别对谐振频点718.59 THz处和722.64 THz处的表面电流进行仿真，仿真结果如图12所示。由图12（a）可以看出，在718.59 THz谐振频点处，顶层和底层的电流流向均沿斜向左下方，产生电共振，形成斜向左下方的感应电场，感应电场沿x方向的分量E1x垂直于入射电场Ei，E1x和Ei之间存在交叉耦合，从而有助于极化转换。由图12（b）可以看出，在722.64 THz谐振频点处，顶层和底层的电流流向均沿斜向右下方，产生电共振，形成斜向右下方的感应电场，感应电场沿x方向的分量E2x垂直于入射电场Ei，E2x和Ei之间存在交叉耦合，从而有助于极化转换。

图12 六重旋转对称结构顶层和底层电流分布

根据以上分析可知，随着“一字”超表面结构旋转对称轴的增加，在可见光频段内的极化转换带宽减小，除了二重旋转对称结构以外，其他多重旋转对称结构的极化转换效率较低。

4 结论

基于三层结构的干涉反射理论，以“一字”反射型线极化转换器为基础模型，分别研究其三重、五重、六重旋转对称对极化转换效率的影响。由仿真结果可知，所设计的结构二重旋转对称时，极化转换效率高于80%的带宽为357 THz；三重旋转对称时，极化转换效率高于80%的带宽为6 THz；五重旋转对称时，极化转换效率高于80%的带宽为0.9 THz；六重旋转对称时，极化转换效率高于80%的带宽为0.3 THz和0.5 THz；随着旋转对称轴的增加，极化转换带宽逐渐减小。