隐伏溶洞与地铁车站深基坑安全距离确定方法
2022-08-24李鹏
李鹏
(中铁北京工程局集团有限公司 北京 102308)
喀斯特地区由于岩溶地层分布大量隐伏溶洞,对地下结构,尤其是大型地铁(超)深基坑基坑的施工安全与质量带来了严重影响[1]。众所周知,地下溶洞不仅影响基坑开挖效率[2],同时还会造成地层缺陷,尤其对于隐伏溶洞而言,不同尺寸与分布特征的溶洞会导致基坑支(围)护结构受力特点千差万别,给基坑设计与施工带来严重困难[3]。
目前,存在多种可有效测量地下宏观孔洞的勘查手段,但对于岩溶地层而言,由于溶洞尺寸离散,分布随机,且多数为聚拢重叠状态,这给超前地质的准确预报带来了一定难度[4]。即使对施工揭示溶洞采取了及时回填支护等措施,但未揭示的临近溶洞仍可对基坑安全构成严重威胁。
目前众多学者采用理论分析或有限元手段,分析了确定溶洞对基坑施工安全的影响,但未阐明溶洞对基坑施工的影响机制,未对临近基坑溶洞的安全距离进行说明,因此无法确定临近基坑的溶洞治理范围和治理效果[5-7]。基于此,本文采用理论分析与数值模拟相结合的方法,首先基于突变理论确定基坑与溶洞之间的安全距离,然后建立基于有限元模型的势函数方法,通过岩层失稳充要条件,提出隐伏溶洞与基坑安全距离的确定方法,为岩溶地层基坑工程设计与施工提供理论依据。
1 突变理论
基坑开挖突变失稳行为即为力学系统势函数达到并超越临界状态的充分必要条件。首先应建立系统势函数,其包括状态变量与控制变量两部分组成,形式如下[8]:

其中,П(x)为势函数,t为状态变量;i和j均为控制变量。
对式(1)求一阶导数,获得平衡状态下的势函数变形表达式,但由于突变模型几何形式为含褶皱的连续曲面,具有流形特性,因此平衡位置不存在确定解,需进一步确定其极限,从而获得其极值稳定态,即:

通常,一个系统往往存在若干个平衡极限点,并沿系统主轴分散分布,进而构造若干个曲面顶点。若突变模型足够精细,则连续曲面顶点沿既定轨道呈变化,即为公式(2)的函数图像。令式(2)等于0,则构建以控制变量为自变量的函数表达式,见图1。控制变量与状态变量在坐标系内构成分叉集,其表达式为:

图1 势函数平衡极限轨迹曲线

当控制变零Ω≤0时,系统状态具有跃迁可能,当Ω>0,系统保持稳定状态。
2 有限元分析
一般地铁深基坑,当基坑开挖至设计标高后,底板未施做且最后一道支撑未设置时,基坑整个支(围)护体系受力最大,基坑变形也达到峰值水平。本研究以贵阳地铁三号线贵州农业大学站为工程案例,已探明该基坑地地连墙后侧存在若干溶洞,最大溶洞等效洞径为2.5m,最小溶洞等效洞径0.4m,溶洞体积比为0.22,即该溶洞分布区域溶洞占总体积比例。因此模型中可利用溶洞比确定溶洞外轮廓边界线,再将最大最小溶洞等效半径作为小溶洞,采用递归算法将确定区域均匀填充。有限元采用映射法划分网格,见图2,下侧采用固端约束,墙土采用半弹性连接,整个模型含2648个单元,材料参数见表1。

图2 基坑地连墙后溶洞有限元模型

表1 材料参数统计表
对于基坑开挖,系统状态变量应变能应考虑所有单元应变增量,即:

式中k为单元编号;n为基坑开挖层数;σ,ε为各单元应力应变值。
将基坑土体开挖过程中各单元对应应力应变求和,即为该基坑开挖的过程能量势函数,利用泰勒公式展开,得到其完全表达式。通常,伴随着基坑开挖,溶洞周围会形成向基坑开挖范围发展的的塑性变形区域,且开挖面越接近溶洞,该塑性区面积越大[9]。由于塑性区随基坑开挖,存在接触基坑开挖面的趋势,但从两者空间距离上很难判断溶洞对基坑的影响程度,因此,本工作以0.5m为增量,计算基坑开挖系统状态的应变能及其状态跃迁行为,再与溶洞诱发塑性区发展水平对比,以此实现溶洞安全距离的准确判断。
由图3可见,基坑开挖过程中,随着溶洞距地连墙的距离增加,溶洞引起的塑性变形区域虽然均会向地连墙方向发展,但区域范围逐渐减小。当溶洞距离地连墙超过其直径的2.5倍后,基坑开挖扰动基本对溶洞无任何影响。

图3 地连墙周围塑性区发展
3 溶洞大小及安全距离
如前文所述,基坑开挖过程中,系统状态势函数二阶导数大于0时,系统状态将发生跃迁,当系统状态小于0时,系统状态维持原状。同理,当基坑开挖有限元模型总能量二阶导数大于0时,基坑系统状态存在跃迁,此时溶洞与基坑距离,即为该溶洞的分布临界距离。
利用不同距离溶洞条件下基坑开挖有限元计算结果,得到不同距离基坑系统的状态变量值,结果见下表。
由表2可见,当溶洞距离基坑地连墙控制参数d/D从洞径的3.2倍缩小至3.1倍时,塑性区开始延伸至基坑区域,但此时Ω值却为5.23,远大于状态跃迁临界值(Ω=0),即此时虽然溶洞影响塑性区延伸至基坑范围,但仍对基坑安全未构成威胁。当d/D继续缩小至2.5时,Ω值才由正直变为负值,即基坑安全临界状态被突破,溶洞作用对基坑开挖安全构成威胁。由此可见,利用能量势函数要比利用塑性区发展判断溶洞对基坑安全要精确的多,其判断依据也更为可靠。
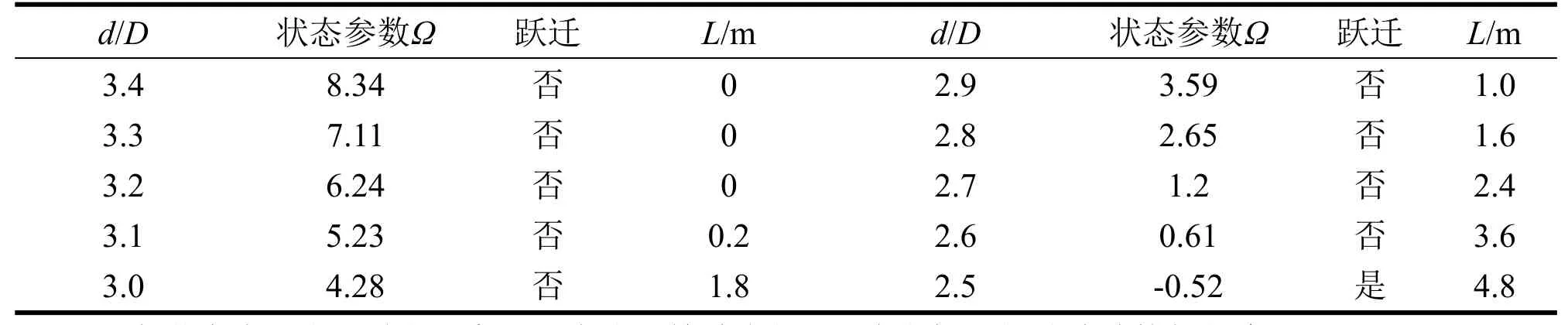
表2 有限元计算结果统计表
综上所述,基于突变理论可得到岩溶地层溶洞距离地铁车站的安全距离,该安全距离可通过d/D进行表征。岩溶地层隐伏溶洞在2.2溶洞比条件下,d/D=2.5为溶洞安全距离判定条件。
4 结论
本文针对隐伏岩溶地层地铁基坑施工过程中溶洞作用塑性区的不利影响,基于突变理论,采用有限元手段,综合对比了距离基坑不同距离溶洞下的基坑开挖的系统能量势函数、状态参数以及塑性区延伸规模,提出了一种适用于岩溶地层的溶洞与基坑安全距离确定方法。主要研究结论如下:
(1)临近基坑溶洞在基坑开挖过程中,可形成具有向基坑发展趋势的塑性应变区,该区域规模与溶洞距基坑距离的增加而减小。
(2)临近溶洞基坑开挖能量势函数可通过所有单元应变能求和得到,其二阶导数即为基坑安全状态的控制函数,当控制参量大于0时,基坑状态发生跃迁,即该状态溶洞对基坑安全构成威胁。
(3)当溶洞距离基坑地连墙控制参数d/D从洞径的3.2倍缩小至3.1倍时,塑性区开始延伸至基坑区域,但此时Ω值却为5.23,远大于状态跃迁临界值(Ω=0)。
(4)当溶洞比为2.2时,岩溶地层基坑开挖的溶洞安全距离为其自身尺寸的2.5倍,当d/D<2.5时,该溶洞可导致基坑发生失稳破坏。
