基于遗传算法的塔器扰度优化设计
2022-08-24韩羲词
仇 放 郭 超 陈 昇 杨 帅 韩羲词
(1.中国石油工程建设有限公司;2.中国特种设备检测研究院)
塔器是石油化工生产装置中常用且核心的设备之一[1],塔器设计需同时兼顾经济成本与使用安全,其中,扰度优化是塔器设计的一个关键点。 由于塔器高径比大、筒体薄,在一定风载荷作用下,大扰度会造成塔盘倾斜振动,影响传质效率和产品质量[2],也会造成局部应力集中(如塔顶接管),导致介质泄漏、引发安全事故[3]。塔器扰度设计需在满足工艺、强度、空间布局和占地要求的前提下,尽可能降低扰度和减小塔器质量来保障运行高效稳定与安全、节省投入成本,实现效益最大化,是一个典型的多目标优化问题。 塔器挠度通常是根据NB/T 47041—2014 《塔式容器》附录C[4],考察塔器总高、直径、壁厚和基本风压影响进行设计,具体过程为按设计压力计算塔体和封头的壁厚,在考虑风载荷、地震载荷和多工况条件下进行强度校核,满足强度要求后对挠度进行控制。 塔器扰度产生主要是因为在风载荷的作用下产生一定的静挠度,塔器所受除风载荷或地震载荷以外的其他载荷(如偏心载荷),比起风载荷或地震载荷要小很多,因而挠度计算可仅考虑风载荷[5]。 为降低扰度,业界常凭设计经验,采用降低塔器总高、增大内径、增加壁厚、减少操作维护平台数量及减少框架支撑等方法[6,7]。但这些方法均存在一些不足:降低塔器总高,增大塔器内径,难以保证工艺要求,会影响塔内气液传质效果;减少操作维护平台数量,不便于工艺管口设计和后期维护检修;增加框架支撑,需要进行二次设计,对空间布局和占地面积要求高;增加塔器厚度方法最简单易行, 但受设计经验影响大,大范围或不合理的厚度增大会造成材料浪费、投入成本大且扰度降低效果不明显。 因此,现有方法难以实现塔器扰度多目标最优化,扰度多目标优化仍是设计的难点。
工程领域中常用的多目标优化智能方法有遗传算法[8]、粒子群算法[9]、蚁群算法[10]及模拟退火算法[11]等。 遗传算法是一种通过模拟自然进化过程搜索最优解的方法,它提供了一种求解非线性、多模型及多目标等复杂系统优化问题的通用框架,通过选择(Selection)、交叉(Crossover)及变异(Mutation)等机制,在每次迭代中都保留一组候选个体,重复此过程,种群经过若干代进化后,理想情况下其适应度可达到近似最优的状态。 该算法以其良好的全局优化性能被广泛用于压力容器设计[12~14],具有代表性的有谢菲尔德大学的遗传算法工具箱[15,16],极大简化Matlab编程,能快速实现遗传算法,从而寻求出全局最优解。 为此,笔者基于NB/T 47041—2014《塔式容器》中扰度计算方法,引入价值指数并采用遗传算法对裙座半锥顶角度和局部塔段厚度进行多目标扰度优化,在满足工艺、强度、空间布局和占地要求的前提下,实现扰度与投入成本最优化。
1 塔器挠度优化的计算基础
1.1 传统塔器挠度计算方法
NB/T 47041—2014《塔式容器》附录C中,图1所示的等直径不等厚度塔式容器顶部挠度y (单位:mm)的计算公式为:

图1 等直径不等壁厚塔式容器挠度计算简图

1.2 价值工程算法
价值工程(Value Engineering,VE)是一门新兴的管理技术用来降低成本提高经济效益,越来越广泛地应用于压力容器等工程领域[17~19]。 价值高,说明该事物的有益程度高、效益大、好处多;价值低,说明有益程度低、效益差、好处少。 价值工程把“价值”(V)定义为“对象所具有的功能(F)与获得该功能的全部费用(C)之比”,即:V=F/C (2)引入价值工程理论,以圆筒形裙座塔器为评价对象,逐步增加裙座半锥顶角来研究挠度的变化。 现以增加设备的质量作为“成本”,以降低的挠度作为“功能”,以“价值”值来判断最优的裙座半锥顶角度。其价值指数Vi以下列公式进行计算:

式(1)中第i个评价对象的功能指数Fi=第i个评价对象的目前功能F/全部功能总和∑F, 第i个评价对象的成本指数Ci=第i个评价对象的目前成本C/全部成本总和∑C。
价值指数Vi=1, 说明增加的质量和降低的挠度比重大体相当,是合理的;价值指数Vi>1,说明增加少量的质量能获得较大的降低挠度,是十分具有“价值”,即增加角度来降低挠度是十分可行的;价值指数Vi<1,说明增加质量导致降低的挠度较少,不具有高“价值”,即不推荐增加角度来降低挠度。
1.3 遗传算法
采用改变塔器裙座半锥顶角度和部分塔段壁厚来降低挠度,事先无法知道最优的角度和塔段壁厚,属于随机模糊问题,就需要遗传算法的全局寻优特点来解决随机模糊计算。 遗传算法计算流程如图2所示。
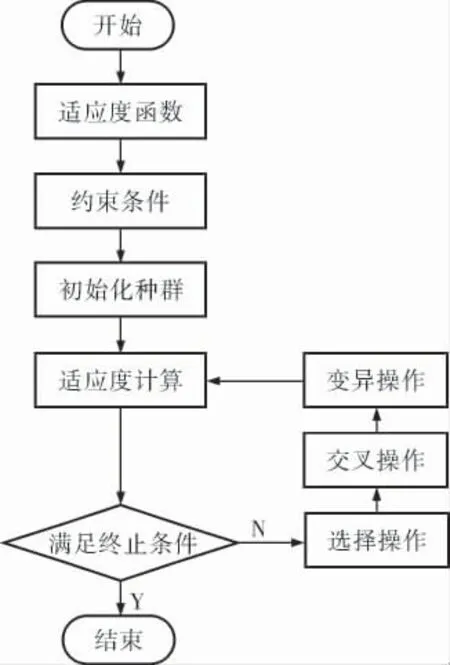
图2 遗传算法计算流程
2 塔器挠度多目标优化
以某天然气处理厂项目脱丁烷塔等直径不等厚度塔式容器为例,其主要设计参数为:内径1 400 mm,筒体切线高度42 100 mm,裙座高度5 500 mm,材料SA537 CL1,设计温度150 ℃,设计压力1.08 MPa,筒体和裙座的腐蚀裕量均为3 mm,基本风压500 Pa,保温厚度130 mm,地面粗糙度类别为B,项目要求挠度y<200 mm。
首先根据NB/T 47041—2014 《塔式容器》进行强度设计,塔器分段长度宜控制在5~10 m[20],分段后的塔段和圆整后的最小名义厚度见表1,以最小名义厚度进行设计, 得到塔器挠度为304.80 mm,无法满足挠度控制要求。 因此,为了降低挠度,原设计方案仍保留圆筒形裙座,采用增加部分塔段筒体壁厚的方法, 拟定3个方案:方案1主要增加裙座厚度(1#~2#段);方案2主要增加塔器底部各段厚度(1#~4#段);方案3为从下往上均匀增加各段厚度。 塔器的最终挠度与质量列于表1。

表1 塔器的分段壁厚、挠度和质量
2.1 关键参数的影响
2.1.1 裙座半锥顶角
在原方案的基础上将圆筒形裙座改为锥形裙座,根据NB/T 47041—2014《塔式容器》可知,半锥顶角不宜超过15.0°, 因此在0.0~15.0°范围内进行研究。 随着半锥顶角的增加、塔器挠度的降低、塔器的质量增加,按照式(3)算得方案1~3的价值指数,并绘制成图3~5。由图3~5可见,3种方案均在半锥顶角为9.3°时Vi=1, 角度继续增加后Vi<1, 因此塔器在半锥顶角增至9.3°之前, 采用通过增大半锥顶角来降低挠度的方法是可行的。

图3 方案1裙座半锥顶角变化的价值指数
方案1~3为圆筒形裙座时, 塔器挠度分别为199.00、198.77、199.32 mm,当采用锥形裙座且半锥顶角改为9.3°时, 塔器挠度分别为156.70、148.34、148.89 mm,降幅分别为21.26%、25.37%、25.30%。 因此,采用增大半锥顶角方法降低挠度,效果十分明显。
2.1.2 塔器壁厚
由上述可知, 将圆筒形裙座改为锥形裙座,半锥顶角在9.3°以内具有高“价值”的可行性。 但是具体改变多少角度和增加多少塔段壁厚才能用最省的材料达到挠度规定值,传统设计无法定量得知,只有采用遗传算法,进行全局寻优,才能找到最优的半锥顶角度和塔段厚度。
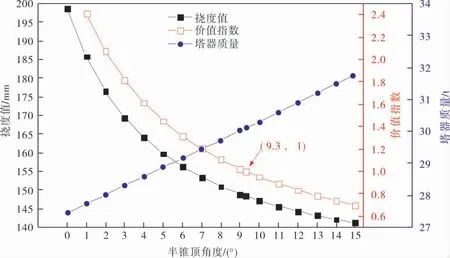
图4 方案2裙座半锥顶角变化的价值指数

图5 方案3裙座半锥顶角变化的价值指数
建立优化设计数学模型的具体细则为:
a. 适应度函数。 塔器总质量为适应度函数,塔器各段的名义厚度和裙座半锥顶角为自变量,共10个自变量。
b. 约束条件。 以基于式(1)的塔器挠度和满足强度设计的各段最小名义厚度为约束条件,此为非线性约束条件,故采用增广拉格朗日遗传算法(ALGA)来解决非线性约束问题。
c. 实数编码。 种群规模取100,交叉概率0.8,变异概率0.05,随机均匀分布选择法,其余采用程序默认参数。
d. 终止条件。 遗传代数超过300代。
笔者建立非线性约束性函数Constraint.m文件为:
function [c,ceq]=constraint(x)
c(1)=Ydeflection(x)-200; %挠度<200mm
c(2)=x(1)-14;c(3)=x(2)-14;c(4)=x(3)-14;c(5)=x(4)-12;c(6)=x(5)-12;
c(7)=x(6)-12;c(8)=x(7)-12;c(9)=x(8)-12;c(10)=x(9)-12;%各段厚度需大于对应段的最小名义厚度
c(11)=x(10)-15; %半锥顶角小于15°
ceq=[];
end
寻优方法一——改圆筒形裙座为锥形裙座。以最小名义厚度进行设计, 塔器挠度为304.80 mm,将圆筒形裙座改为锥形裙座,半锥顶角设定在9.3°,塔器挠度为224.14 mm,塔器质量为22 870 kg。
寻优方法二——直接增加塔段壁厚。 运用遗传算法在约束条件中将挠度设定为224.14 mm,经过136代计算, 得到各塔段厚度分别为23、19、17、15、12、12、12、12、12 mm(图6),塔 器 质 量 为24 922 kg。
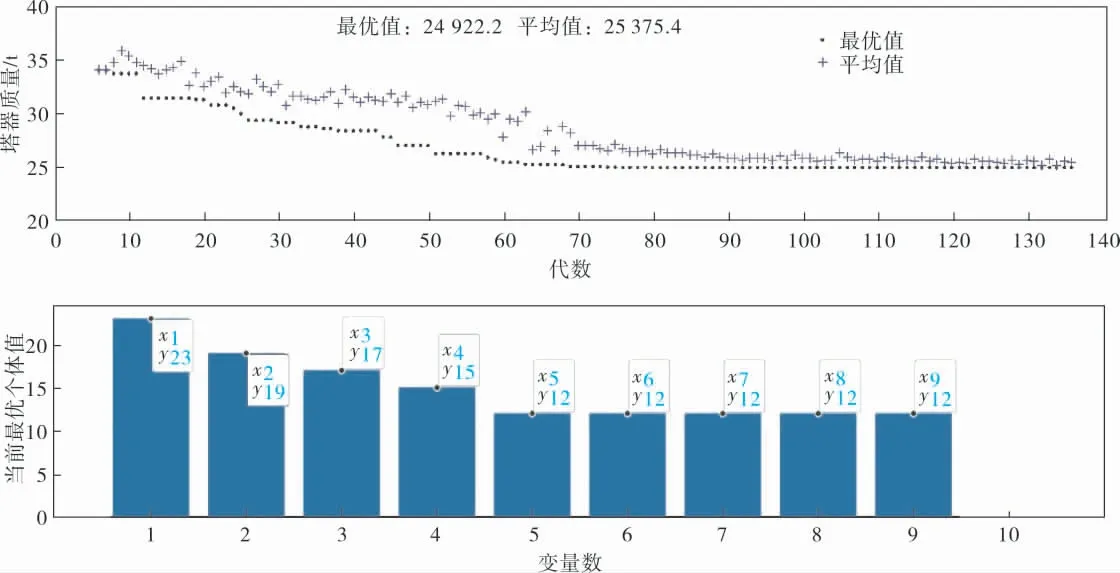
图6 圆筒形裙座塔器挠度为224.14 mm的最优解
综上可知,采用改变半锥顶角的方法比直接增加塔段壁厚的方法可以节约钢材2 052 kg。 因此,降低塔器挠度优先考虑将圆筒形裙座改为锥形裙座。
由遗传算法计算还可以得出,增加塔段壁厚来降低塔器挠度的方法,应优先增加1#~3#塔段壁厚,且增幅相较于4#塔段以后的要大很多。
2.2 挠度综合优化
本实例要求塔器挠度控制在200 mm以内。由前述可知,改圆筒形裙座为锥形裙座,半锥顶角为9.3°时,塔器挠度降低为224.14 mm,无法满足挠度控制要求。 因此,需再次运用遗传算法,将约束条件中挠度设定为200 mm,半锥顶角约束设置为0.0~9.3°。 经过194代计算,各塔段厚度分别为14、19、16、12、12、12、12、12、12 mm, 半锥顶角为8.836°(图7),塔器质量为24 097.5 kg,即为改锥形裙座与增加塔段壁厚相结合的最优降低塔器挠度的计算解。

图7 优化设计最终解
工程上,壁厚需圆整为偶数,因此最终设计方案各塔段厚度分别取16、18、16、12、12、12、12、12、12 mm,半锥顶角取8.9°,此条件下塔器质量为24 529 kg,实际挠度为198.43 mm,可见能满足设计要求。 另外,对比表1中3个拟定的设计方案,塔器质量分别减轻2 602、2 919、4 993 kg,降低了设备的材料费用和建造费用。 综上,可归纳出塔器挠度优化设计的流程如图8所示。
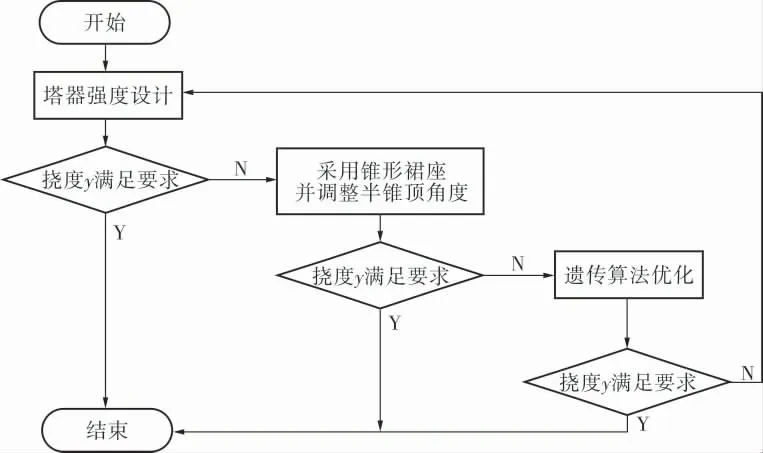
图8 塔器挠度优化设计流程
3 结论
3.1 运用价值工程理论得出, 通过将圆筒形裙座改为锥形裙座的方法来降低塔器挠度的效果明显,且半锥顶角在9.3°以内均具有高“价值”和高可行性。
3.2 可通过增加塔段壁厚的方法来降低挠度,其中优先增加塔底第1段、 第2段和第3段的厚度。
