基于近似技术的双层规划进化算法
2022-08-24沈瑜李和成陈黎娟
沈瑜,李和成,陈黎娟
(青海师范大学数学与统计学院,西宁 810008)
0 引言
在工程和经济管理领域,经常出现具有递阶结构的决策问题,这类问题中决策者处在不同的层次上。首先,处在上层的决策者为了优化自己的目标,提出一个决策方案;处在下层的决策者根据上层提供的方案,选择一个下层问题的最优决策方案并反馈上层;上层结合下层反馈的方案评价自己给出的方案,该过程持续进行,直到使上层目标达到最优。这类具有递阶嵌套结构的优化问题称为多层优化问题[1],其中双层规划问题(BiLevel Programming Problem,BLPP)最为常见,一般模型可表示如下:

式(1)和式(2)分别称为上层问题和下层问题。其中:x=(x1,x2,…,xn) ∈Rn和y=(y1,y2,…,ym) ∈Rm分别称为上、下层问题的决策变量;F(x,y):Rn+m→R 是上层问题的目标函数,f(x,y):Rn+m→R 是下层问题的目标函数;G(x,y):Rn+m→Rp和g(x,y):Rn+m→Rq分别为上层和下层问题的约束函数。式(1)的决策过程可以表述如下:首先上层决策者在上层可行区域选择一个变量值x。将x作为一个参数,求解下层规划问题(2),得到下层规划问题(2)的最优解y。如果得到的(x,y)满足上层问题(1)的约束条件,则称(x,y)为双层规划问题(1)~(2)的一个双层可行点。求解式(1)~(2)的目的就是在可行解集中选择使上层目标F(x,y)最小的双层可行点。如果对于一个给定的上层变量x,下层问题存在多个最优解y与其对应,这种情况涉及下层最优解的选择,不同的选择模式有不同的双层规划模型[2]。为了使双层规划问题结构简洁,在设计算法时更多地关注问题的递阶结构,现有的文献通常假设下层问题的最优解是唯一的[3]。本文的目的是提高算法处理递阶结构的能力。因此,仍然保留下层问题最优解唯一的假设。
双层模型的应用领域很广泛。在农业生产中,使用化肥可以提高生产率,但过度使用会导致环境污染,针对这类问题,文献[4]设计了一个双层模型研究化肥对环境的影响;文献[5]讨论了核武器拦截、关键基础设施捍卫等安全问题,建立了相应的双层规划模型;文献[6]开发了一种基于双层互补模型的决策工具,用于确定贫乏市场中最有利的交易;文献[7]针对整车物流服务供应链的订单分配问题,提出了考虑多种运输方式的双层订单分配模型。双层优化模型的其他应用,参见文献[8-11]。
目前求解双层规划问题的方法主要可分为三大类:
1)基于梯度的经典优化方法。文献[12-13]利用K-K-T(Karush-Kuhn-Tucker)条件将双层规划转化为单层规划问题,但转化后的模型具有复杂的约束域;针对整数线性双层规划,文献[14]提出了一个分支定界法;文献[15]利用K-K-T 条件和最优值条件将双层模型转化为单层优化模型,通过求解单层问题获得原问题的最优解;对于弱线性双层规划问题,文献[16]给出了一个罚函数法;文献[17]利用罚函数法和K-K-T 条件设计了求解非线性双层规划问题的算法。这些经典的优化方法在求解速度上相对较快,但大部分算法要求函数具有凸可微或线性等性质,普适性不高。另外,分支定界方法在问题规模较大时,计算量增长很快,很难推广到大规模问题。
2)进化方法。文献[18]针对分类特征选择的双层规划设计了一种新的遗传算法;文献[19]针对下层为线性分式的非线性双层规划问题提出了一种基于二进制编码的遗传算法;文献[20]研究了一类区间双层规划问题,提出了一种基于线性分式最优性条件的进化算法;针对一般的非线性双层规划问题,文献[21]提出了一种协同进化算法;文献[22]基于新的选择方式和混沌搜索方法,设计了一种改进的遗传算法;为了求解随机双层规划问题,文献[23]提出了一种基于空间系统采样技术的元启发式算法。单一的进化算法虽然不需要函数凸可微,具有较好的普适性,但是往往会涉及过多的适应度函数评估,产生较大的计算量。
3)混合方法。文献[24]提出了一种基于模拟退火Metropolis 准则的改进粒子群优化算法,该算法设计的目的是解决粒子群优化算法求解双层规划问题时易陷入局部最优解的问题;文献[25]提出了一种混合启发式方法求解p中值双层问题;对于单目标双层规划问题,文献[26]提出了一种将全局搜索和局部搜索结合的模因算法;文献[27]提出了基于多种群的多正弦余弦算法;文献[28]提出了采用灵敏度分析技术的粒子群分布估计算法。混合方法结合多种算法的优势处理双层问题,整体搜索效果好。然而,由于算法的复合结构,嵌入算法的节点、参数的调试是个比较复杂的问题,直接影响算法的求解效率。
众所周知,导致双层规划问题计算量大的原因是频繁计算下层问题。因此,要想显著降低双层规划的计算量,必须减少下层问题的求解次数。Sinha 等[29]利用多值映射的方式近似下层解函数,Liu 等[30]利用插值函数近似下层问题的最优解,这些近似技术极大地提高了算法的计算效率,但不足的是需要构造插值函数或映射,且更新过程的计算量随问题规模的增加快速增长,本身也会产生较大的计算量。
为了解决上述问题,本文针对具有上下层约束的一般双层规划,基于参数规划的最优解理论,提出了一种基于下层解近似技术的进化算法。与现有的近似技术相比,本文算法不需要设计近似函数,在获得下层最优解方面能真正减少计算量。
1 基本概念
本文讨论的双层规划问题中,上下层函数没有特殊限制,这一点与线性、二次等特殊模型不同,更有一般性。为了叙述方便,引进一些符号和概念[3]。


2 本文算法
本文算法采取了多种群协同进化的模式。协同进化不仅考虑了局部个体信息的充分交换,而且为下层解的近似估计提供了便利。下面分别给出算法的各个关键环节。
步骤1 种群初始化。
首先在上层可行区域内均匀产生K个点xck(k=1,2,…,K),即K个上层变量值;然后,在以这K个点为中心的邻域内均匀产生-1 个点。共得到M个点,不妨设这M个点均在上层决策空间的投影区域内,如若不然,重新产生即可。这些点组成规模为M的初始种群,个体记为xi(i=1,2,…,M)。同时,这些个体根据与K个中心个体xck的距离聚类为K组,即,初始种群P(0)由K个子种群P1、P2、…、PK组成,每个小种群包含个个体。将xi(i=1,2,…,M)代入下层问题中解出下层问题的最优解yi(i=1,2,…,M)。令代数t=0。
步骤2 个体评估。
以上层目标函数F(x,y)为适应度函数。根据评估结果,选出种群中最好的个体,并存储在最优解集合A中。
步骤3 交叉操作。
由于参数优化理论,最优解对参数具有一定的依赖性,因此,本文算法中交叉后代尽可能在距离较近的个体之间产生。在子种群Pk(k=1,2,…,K)中,以交叉概率Pc随机选择两个距离较近的个体xi和xj进行交叉操作,产生的后代个体为:

其中:λ∈(0,1)。根据产生的xc,对应的下层最优解通过如下方式近似:
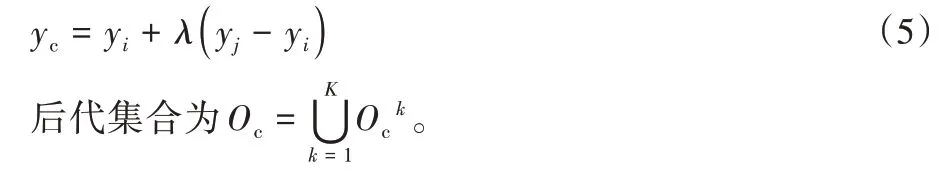
交叉过程如图1(a)所示。交叉父代个体处于上层决策空间中,实心圆点和空心圆点表示随机选择的父代个体,小三角表示交叉后代。下层决策空间中,实心圆点和空心圆点表示父代个体对应的下层最优解,小三角表示交叉后代的下层近似解。子种群的设计限定了交叉父代个体之间的距离,在一定程度上保证了近似解的准确性。
步骤4 变异操作。
在种群P(t)中,以变异概率Pm随机选择个体xi进行高斯变异操作,其后代个体为:

并给出其对应的近似下层最优解:

其中:β~N(0,1)。
计算后代个体xm与K个中心个体(k=1,2,…,K)的距离,并将变异后代放入距离近的子种群。
变异过程如图1(b)所示:上层决策空间中,实心圆点表示父代个体空心圆点通过高斯变异产生的后代个体;下层决策空间中,空心圆点表示父代个体对应的下层最优解,该点进行同样的变异操作产生的后代个体是对应的下层近似最优解(实心圆点)。在种群中进行的变异会在这个约束域内产生点,具备全局搜索的功能,有助于保持算法的开采能力。

图1 交叉操作和变异操作示意图Fig.1 Schematic diagrams ofcrossover operation and mutation operation
步骤5 后代个体预评估。
对于产生的后代个体,包括交叉个体和变异个体,计算下层近似最优解yi,然后将(xi,yi)代入上层目标函数和约束函数。若(xi,yi)不满足约束,则赋予较大的目标函数值;否则,以上层目标函数值为该个体的预评估值,之所以称之为预评估值,是因为下层并没有获得精确的最优解。
步骤6 验证后代种群的拟合程度。
在子种群Pk(k=1,2,…,K)中,随机选择M3K个较好个体进行验证。验证过程如下:将经过交叉或变异操作后的个体xi代入下层问题中,得到其精确最优解,则对应的精确可行解为(xi,)。比较F(xi,yi)与F(xi,)的大小关系。若式(8)成立,则认为拟合程度好;反之,则认为拟合程度不好。
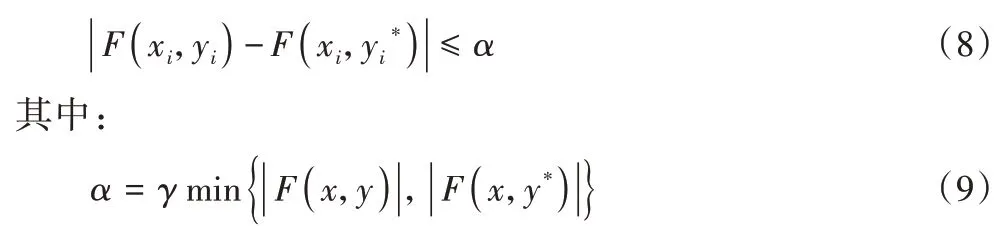
γ为充分小的正数;α为拟合系数,α值越小说明拟合程度越好,反之亦然。根据拟合程度检验,通过设定阈值,可得到拟合程度较好的子种群和拟合程度较差的子种群。
步骤7 选择操作。
步骤8 算法停止。
如果满足停止标准,则输出集合A中的解;反之,令t=t+1,执行步骤3。
本文算法流程如图2 所示。
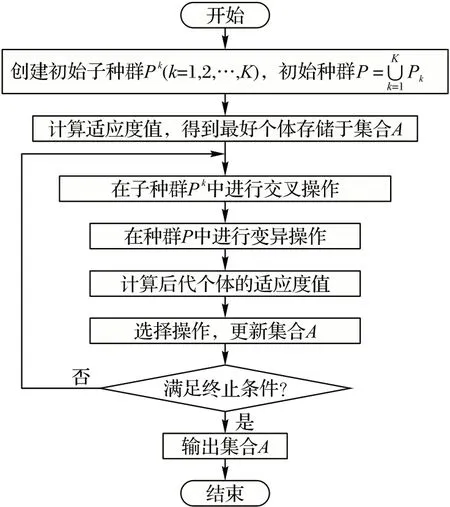
图2 本文算法的流程Fig.2 Flowchart of the proposed algorithm
本文算法的主要目的是减少下层问题的计算频次,最终达到提高计算效率的目的。首先根据欧氏距离对种群个体进行聚类形成子种群,其次交叉在子种群内部进行。由于个体间的距离较近,因此,两个父代个体交叉产生的后代在父代个体附近。考虑到上层变量的不同只导致下层问题参数的不同,基于灵敏度分析理论,最后采用比例近似技术估计后代个体对应的下层最优解。这个技术有效避免了对下层问题的频繁求解,减少了计算量,这是与现有算法的本质不同。
本文算法对问题涉及的函数、变量等无特殊要求,具有较好的普适性,因此,可用于处理线路优化、软件设计、资费设置等领域内的双层规划模型。
在双层规划常见的算例中任选一个,具体如下:

对于∀x∈[0,5],式(10)的诱导区域为:

在图3 中,实线部分为式(10)的诱导区域。在种群进化过程中,抽取了10 对父代个体,给出了对应后代及近似下层解,并对每个后代计算了精确的下层最优解。所有数据见表1。

图3 式(10)的诱导域Fig.3 Inducible region of Equation(10)
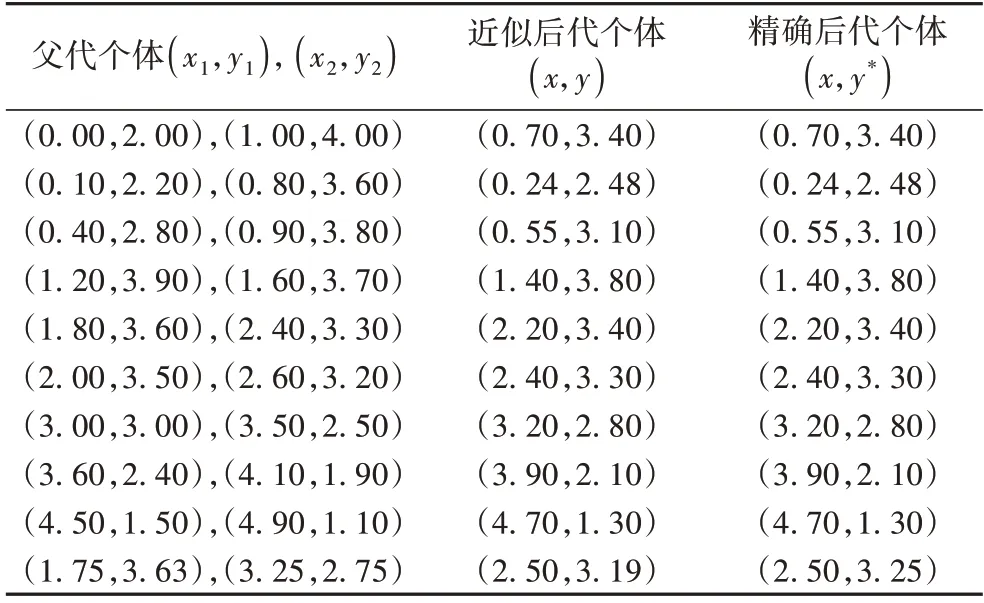
表1 近似下层解和精确下层解Tab.1 Approximate and precise follower solutions
表1 数据显示,大部分下层最优解小数点后两位是一致的,仅仅最后一个个体出现了大于10-2的误差,说明由近似技术得到的后代个体准确性较高。表2 给出了近似解的目标函数值和精确解的目标函数值,它们的绝对误差均小于给定的阈值(最后一列,取γ=0.01)。根据表1~2 中的数据分别绘制拟合曲线,见图4~5。从图4~5 的曲线和点的拟合程度可知,由近似技术得到的近似后代个体与精确后代个体的位置大部分是重合的,意味着本文提出的近似技术是可行有效的。
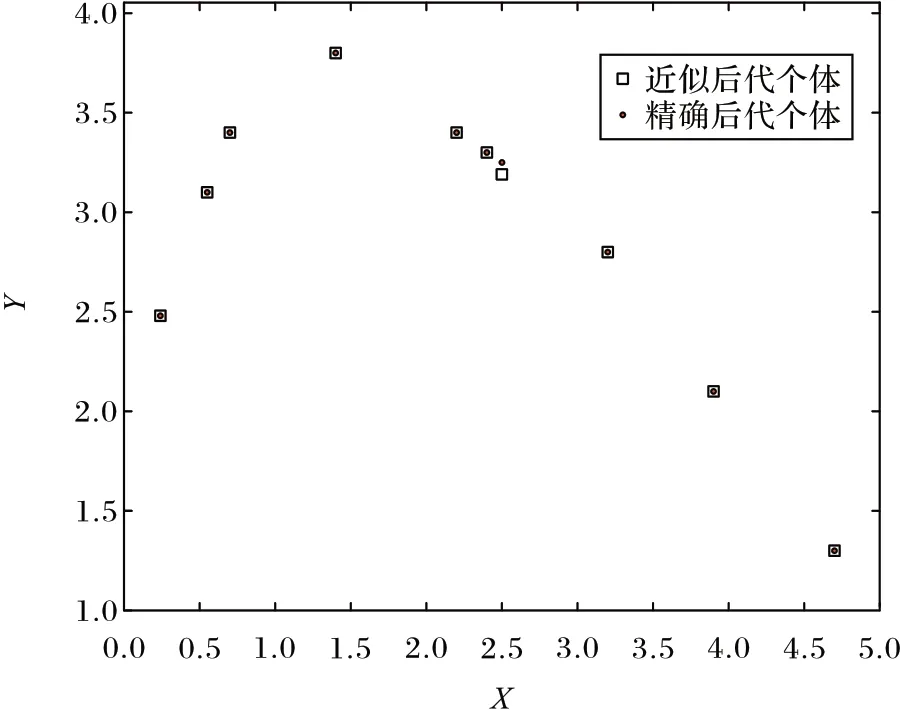
图4 下层解的散点图Fig.4 Scatter diagram of follower solutions

表2 目标函数值的误差Tab.2 Errors of objective function values
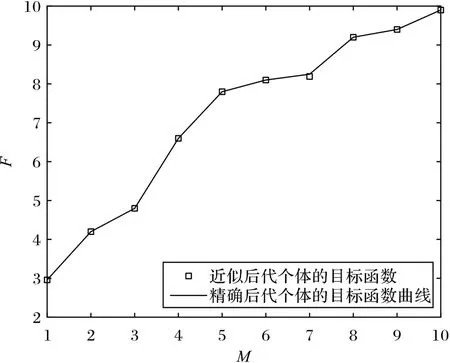
图5 目标函数曲线图Fig.5 Curves of objective functions
3 数值实验
3.1 测试函数与应用算例
算例1[31]:



本文选取了10 个算例作为测试函数,其中,算例1~2 是整数线性双层规划,选自文献[31];算例3~5 是混合整数双层规划,选自文献[32];算例6~10 是一般类型的双层规划,选自文献[29]。算例1 的上层决策变量的维数是4,下层决策变量的维数是2;算例2 的上层决策变量的维数是4,下层决策变量的维数是3,并且上层规划问题是一个0-1 规划问题。算例6~8 的上层或下层目标函数是二次函数。算例10的上层目标函数是不可微的,下层目标函数是二次函数。这些算例是双层规划算法常见的测试函数。本文算法在这10个算例上分别进行了仿真测试。
为了说明本文算法在求解实际应用问题方面的有效性,考虑实践常见的资费设置问题,该问题的模型如下:

其中:集合G表示起点-终点的组合;集合D表示网络图中点的集合;集合B表示的是网络图中弧(路)的集合。B1表示收取通行费的弧(路)的集合,B2表示不收取通行费的弧(路)的集合。在双层规划模型中,上层决策变量xa表示道路a∈B1的通行费用,由上层决策者直接控制;下层决策变量表示起点到终点的车流量。i+(i-)表示以i作为起点(终点)的路的集合。每一条路a∈B都提供了驾驶这条路的行驶成本ca,该成本不包括通行费用。对于每一组g∈G,从起点o(g)到终点d(g)的需求车辆数为ng。上层目标函数(12)需要使收费站的收益最大化,下层目标函数(13)倾向于使用户的支出最小化。
该模型对应的网络拓扑结构见图6,其中:

图6 道路网络拓扑Fig.6 Road network topology

为了简洁,记该应用算例为算例11[33]。
3.2 实验参数设置
实验中用到的参数取值如表3 所示,对每个测试函数算法独立运行20 次,记录得到的最优解。

表3 相关参数及取值Tab.3 Related parameter and their values
3.3 实验结果与分析
表4 中测试算例1~10 为独立运行20 次后上层目标函数的最好值、最差值和均值,对比算法为文献[31-32,29]算法;算例11(应用实例)的对比算法为文献[33]算法。
从表4 可看出:

表4 上层目标函数值的最好值、最差值和均值Tab.4 Best values,worst values and mean values of leader objective functions
1)前10 个算例中,本文算法相较于对比算法,找到的最优解相同或更好(算例8 为更好)。本文算法找到每个算例上层目标函数值的最好值、最差值和均值都一致,说明算法稳定可行。在测试算例8 上,本文找到的上层目标函数值(最好值、最差值和均值)都比相应文献中的最好值好,说明本文算法有较强的全局搜索能力。
2)对于算例11(应用实例),本文算法找到了比文献[33]算法更好的上层目标函数值,并且上层目标函数最好值、最差值和均值一致,说明用该算法求解应用实例——资费设置问题是可行有效的。
表5 为10 个测试算例上获得的最优解对比,表6 为最优解对应的下层目标函数值对比。从表5~6 可看出,本文算法在算例8 中均能找到更好的最优解。

表5 本文算法和比较算法的最优解对比Tab.5 Best solutions comparison of the proposed algorithm and compared algorithms

表6 最优解对应的下层目标函数值Tab.6 Follower objective function values corresponding to best solutions
为了检测算法的计算时间,以算法找到最优解为停止标准,记录了算法找到最优解时的平均CPU 时间(CPU)。为了显示近似技术的有效性和比较的公平性,以本文算法为框架,对每个上层变量均求解下层问题,同样以该算法找到最优解为停止标准,获得下层最优解,记录算法所需的CPU 时间(Update All CPU,UACPU),所有数据见表7。由表7 可知,UACPU 时间较长,CPU 时间较短,说明近似技术能有效提高找到最优解的速度,减少运行时间。对于求解资费设置问题,本文算法能提高计算效率。
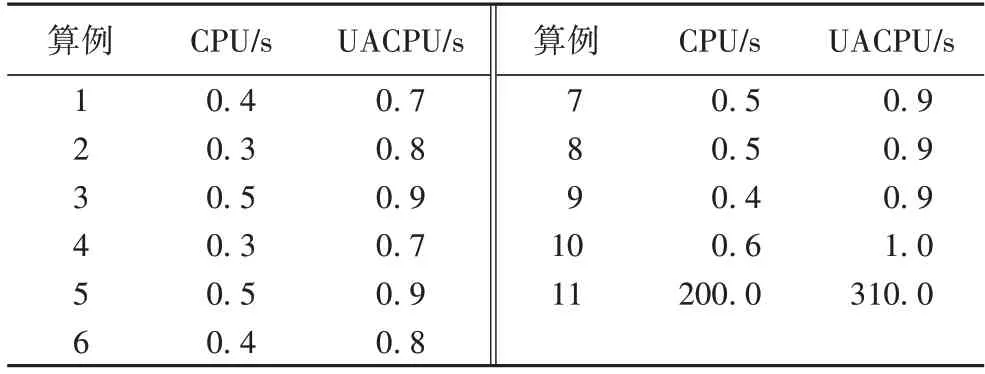
表7 本文算法的CPU时间和UACPU时间比较Tab.7 Comparison of CPU time and UACPU time of the proposed algorithm
4 结语
为了减少双层规划的计算量,本文提出了一种基于近似技术的进化算法。本文算法通过多种群协同进化的方式,仅仅求解部分下层问题,由近似技术得到下层问题的近似最优解,并根据小种群的拟合程度选取下一代个体,最终获得问题的全局最优解。本文算法在保证计算精度的同时,节约了大量的下层计算量。本文算法未构造插值函数和映射,在计算框架上更简洁。
下一步,将研究算法中一些关键参数的取法,在自适应分组、近似技术改进等方面开展工作,提高算法在解决复杂优化问题方面的效率。
