基于改进模板匹配算法的物料计数方法研究
2022-08-23陈晓荣张彩霞郭蓉蓉王晓龙
韩 硕, 陈晓荣, 张彩霞, 郭蓉蓉, 王晓龙
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
随着科技的高速发展,各领域对物料计数的要求也在大幅度提高。目前,物料计数方法主要有人工检测法、称重法和光电检测法等。其中,人工检测法的工作强度大、效率低并且容易受到主观因素的影响,导致计数准确率不高。称重法对物料的质量均匀性要求较高,容易因为物料之间的差异性造成计数错误。光电检测法更适用于物料依次通过的情况,在多个物料并排通过或者发生粘连时容易出现计数错误,并且光电管存在一定程度的滞后反应,使计数准确度降低,无法满足工业生产中实时、高效的计数检测要求[1]。针对上述情况,研究能够对物料进行自动计数的检测方法,可以有效提高检测效率和准确性。由于要保证物料计数的实时性,所以采集的每1幅图像较小,1个完整的物料无法呈现在1幅图像中。随着数字图像处理技术的进步而发展起来的图像拼接技术则为这一问题提供了很好的解决方法。
Lowe[2]等提出了尺度不变特征变换(scale-invariant feature transform,SIFT)算法,可在图像中检测出关键点进行匹配,并且不受光照影响,但是当待测物体出现较大形变时,其匹配准确度较低;Brown[3]等提出了一种称为Auto Stitch的全局对齐方法来自动缝合多幅图像,但当场景接近平面时,可能会出现错位和伪影,导致具有视差的图像无法精确对齐;张见双[4]等提出Harris角点检测算法提取图像中的特征点,结合使用RANSAC剔除误匹配点,提高了匹配精度,但是该算法对尺度较敏感,并且其消耗的时间较长;Hu[5]等提出图像高斯金字塔变换(Gaussian pyramid transformation,GPT)匹配算法,采用遍历匹配方法保证了匹配的准确性,但是用时较长;Gong[6]等提出使用粒子群算法(particle swarm optimization,PSO)搜寻最佳匹配位置,减少了匹配次数从而缩短匹配时间,但是易过早收敛陷入局部解,容易导致匹配准确性不高。上述方法取得了一定效果,然而拼接时间较长并且在图像匹配准确度上依然存在一定的缺陷。
模板匹配算法(template matching algorithm,TMA)是一种图像拼接算法,TMA与SIFT、GPT和PSO等算法相比,具有原理简单、适用面广、鲁棒性能好等特点[7~9],然而TMA算法匹配的搜索范围较广,算法运行时间长。本文在传统模板匹配算法的基础上,提出了一种基于双模板搜索方式和位置约束r的改进模板匹配算法(improved template matching algorithm,ITMA),将ITMA与Canny边缘检测算法相结合,通过Canny边缘检测算法求解ITMA模板,求出最优边缘,从而获得最佳的模板图像,然后对图像进行拼接,实现物料计数。
2 Canny边缘检测算法
Canny边缘检测算法是Canny于1986年研究出来的一个多级边缘检测算法[10~13],本文采用Canny边缘检测算法来检测图像的边缘像素可以做到降低错误率,精确定位到物料边缘位置,便于后续物料图像的匹配。Canny算法具体步骤为:
步骤1:高斯滤波。由于受到拍摄硬件设施、采集环境等因素的影响,导致采集到的图像存在截然不同的成像特性,这些特性对后续算法处理有很大的影响。为了尽可能减少噪声对边缘检测结果的影响,采用高斯滤波完成图像去噪,便于后续对图像的边缘检测。
(1)
式中G(x,y)是标准差为σ的二维高斯核。
平滑后图像g(x,y)表示为:
g(x,y)=f(x,y)*G(x,y)
(2)
式中f(x,y)为初始图像。
步骤2:计算梯度值和梯度方向值。灰度强度变化最强的位置即梯度方向,通过计算水平方向梯度Gx和垂直方向梯度Gy来检测图像中的水平、垂直和对角边缘,即可确定像素点的梯度幅值和方向。
水平方向的梯度为:
(3)
垂直方向的梯度为:
(4)
该像素点的梯度的幅值和方向分别为:
(5)
θ=arctan(Gy/Gx)
(6)
步骤3:进行非极大值抑制。对图像进行梯度计算后,并不能够提取出比较清晰的边缘,需要使用非极大值抑制来寻找像素点的局部最大值,将非极大值点所对应的灰度值抑制为0,这样就可以筛除一部分不属于边缘的点。
3 改进模板匹配算法
3.1 传统模板匹配算法
模板匹配算法是寻找待测图像中具有模板图像相同特征的算法之一,其寻找待测图像中的每一个可能的位置,计算模板的所有相关位姿与图像各个位置的相似度,当相似度足够高时,则认为找到目标[14~20]。该算法相较于其他匹配算法,易于实现,匹配速度较快,因此本文选用模板匹配算法作为图像拼接的主要方法。
模板匹配算法的基本思想是首先确定模板图像,以模板图像T与待测图像S的原点为参考点,使模板图像T在待测图像S的区域内以平移的形式进行搜索,待测图像被模板覆盖的区域为子图Si,j。搜索范围为:
1≤i≤W-M
(7)
1≤j≤H-N
(8)
式中:M,N表示模板图像T的像素个数;W,H表示待测图像S的像素个数;i,j为模板覆盖区域左上角在待测图像S上的坐标。
通过比较模板图像与待测图像中被模板图像覆盖区域的相似度,完成模板匹配过程。归一化相关系数衡量模板T和子图Si,j的匹配程度,其计算式为:
(9)
式中:R(i,j)表示(i,j)处图像的相关系数,0≤R(i,j)≤1;(s,t)表示在模板内的所有像素点;E(Si,j)、E(T)分别表示(i,j)处待测图像和模板图像的平均灰度值。
模板匹配就是寻找最佳匹配位置的过程,归一化相关系数R越大,待测图像与模板的相似度越高;当模板在待测图像上搜索所得最大R(i,j)时,其对应的点(i,j)就是最佳匹配位置,则完成图像匹配的过程。
3.2 改进模板匹配算法
由于模板匹配算法存在难以实现实时性的缺点,本文提出基于双模板搜索方式和位置约束系数的改进模板匹配算法(ITMA)来提高传统算法的运行速度和准确度。
3.2.1 双模板搜索方式


图1 双模板搜索示意图
由于采用背光照射方式采集图像,待测图像目标与背景灰度值相差较大,且目标灰度值小于背景灰度值,所以小于待测图像灰度平均值E(S)的区域即为目标像素区域;在缩小匹配区域后,可得到待测图像目标像素区域高度hs,最后在目标像素区域内寻找与模板匹配的区域即可,从而减少了算法的运行时间。
3.2.2 位置约束系数r
在待测图像目标区域中,同时也存在与模板不匹配的区域,会导致模板匹配过程中寻找最佳匹配位置时出现误差。为了提高匹配的准确度,本文加入一个位置约束系数r,以减少待测图像目标区域与模板不匹配的区域。
令搜索区域F=rhs,其中:
(10)
式中:gr表示模板图像重心的高度;gs表示待测图像目标区域重心的高度。
综上所述,将位置约束系数r作为匹配时求取最优解时的约束条件,结合归一化相关系数R(i,j)可以精确求取最优解。
3.3 基于ITMA算法的步骤与流程
将本文提出的图像拼接算法ITMA与Canny边缘检测算法相结合,用Canny边缘检测算法求最优模板图像,为匹配做最佳准备。
步骤1:获取最优模板图像T。利用Canny边缘检测算法提取物料图像最佳边缘特征,作为最优模板图像。
步骤2:双模板搜索。将模板图像T分成T1和T2两部分并计算图像灰度平均值E(S),在待检测图像S上进行双模板搜索。灰度值小于E(S)的区域记为目标区域D1,反之则记为背景区域D2。
步骤3:约束目标区域D1。将位置约束系数r作为匹配求取最优解时的约束条件,约束条件为式(10)。
步骤4:获取匹配最优解。根据式(11)计算模板和检测到的与模板相匹配的图像误差,并结合式(9)获取匹配最优解。
(11)
式中E(i,j)为最小值即为匹配目标。
步骤5:判断E(i,j)得到最小值和R(i,j)得到最大值的匹配目标是否为同一目标。如果是同一目标则记为Sbest,Sbest为最佳匹配目标。否则重复步骤2~步骤5。
3.4 物料计数
物料在运动过程中存在一些影响因素,导致物料计数有一定的复杂性[21,22]。主要分为2种情况;第1种是每个物料之间互相独立;第2种是物料之间存在一定的粘连。具体物料计数步骤为:
步骤1:取得单个标准样本的面积特征作为判定物料是否存在粘连的准则。
步骤2:双峰法阈值分割。由于采用背光照射方式,物料全景图中目标与背景灰度对比度相差较大,所以采用双峰法阈值分割。将灰度值0和平均灰度Kr分别作为阈值分割的最小阈值和最大阈值,准确分割出背景与目标,对分割后的目标连通域进行计数。
步骤3:判断是否存在物料粘连。将连通域区域面积与单个标准样本面积进行对比,判定大于单个标准样本面积的区域存在物料粘连。
步骤4:断开粘连部分。先对物料区域进行填充,减少腐蚀对存在孔洞的物料的影响,再通过腐蚀将物料粘连部分断开。
步骤5:物料计数。将粘连断开后,通过对处理后的全景图像的连通域进行计数,得到物料数目。
4 实验结果及分析
4.1 实验平台搭建
根据物料下落特点,设计了一套图像采集装置,整个装置包括1个面阵相机、1个LED光源、1个置物架以及1个接收掉落物料的盒子,如图2所示。
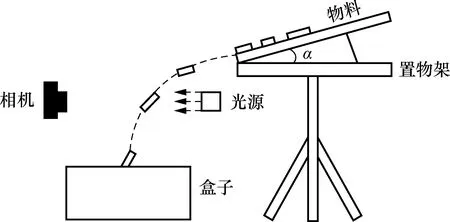
图2 图像采集装置图
在设计图像采集装置中,曝光时间、曝光速度和照明方式是其中非常重要因素。曝光时间决定了图像的清晰度;曝光速度决定了在相同采集环境下,采集到的多幅图像中每相邻的2幅图像之间是否存在重叠的部分;照明方式则会影响图像的成像效果以及后续图像处理所需的时间[23]。为方便后续物料图像拼接,尽可能使采集到的连续图像之间存在重叠区域,因此需要根据物体下落速度设置曝光速度,物体下落速度越快,设置的曝光速度则需越大。经过大量实验,曝光速度设置在800~1 200帧/s之内可以满足本实验中的物料拼接要求。本文中相机参数设置见表1所示,采用背光照射的方式使背景与目标产生较大的灰度差,突出物料图像的边缘特征。

表1 采集过程中相机参数设置
4.2 实验结果
本文采用安全带插片、大蒜、小铲子3种物料作为实验样本,由于采集到的单帧图像无法显示1个完整物料,每1种单个完整物料存在于多帧图像中,其中每1种单个物料在掉落过程中按照采集顺序得到的连续10帧图像如图3所示。
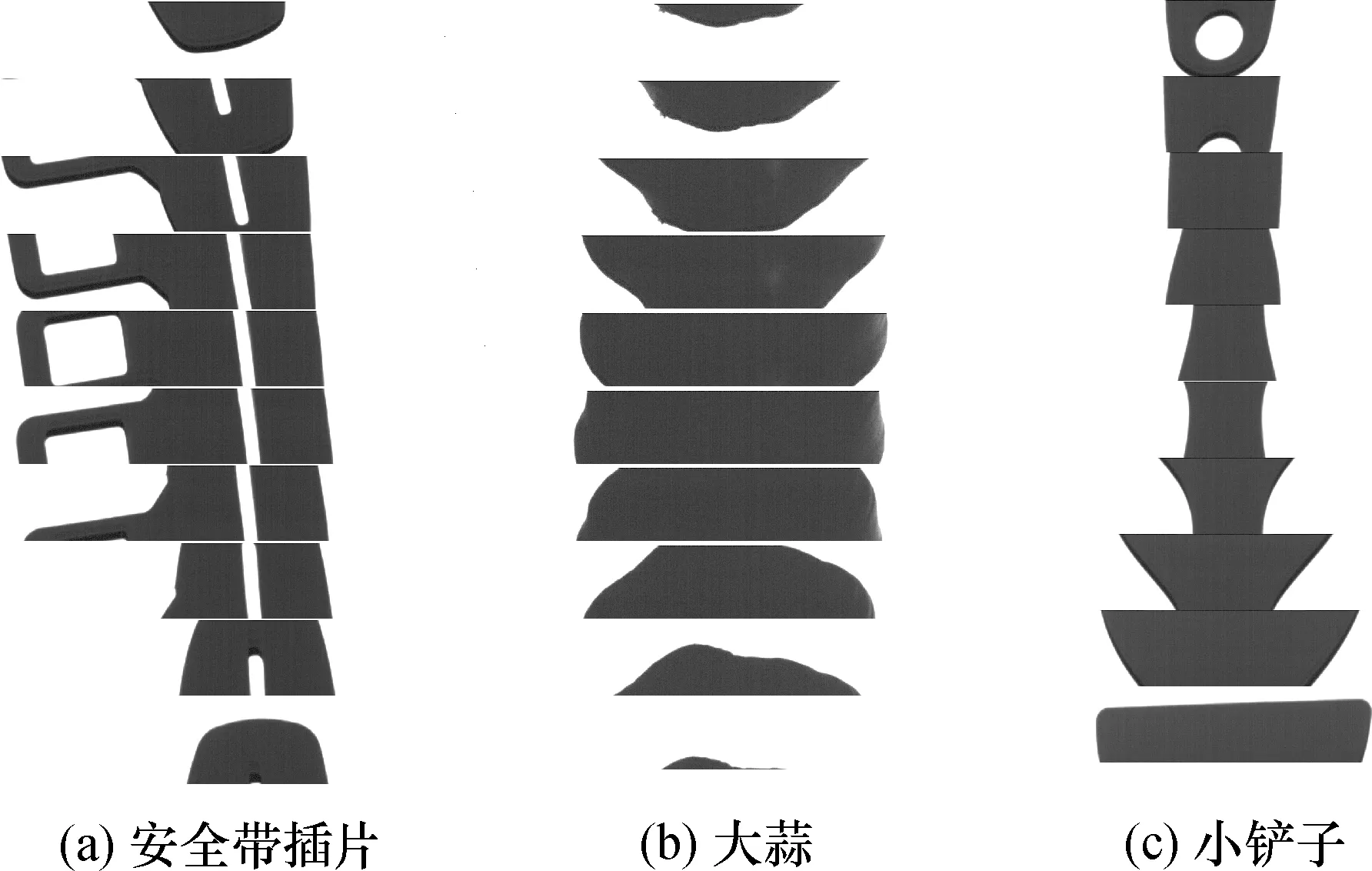
图3 采集到的物料图像
为验证本文算法优化效果,分别用传统TMA算法、GPT优化TMA算法[5]和本文算法对3种物料进行实验,图4为在相同环境下分别对安全带插片、大蒜和小铲子进行拼接实验效果图。

图4 3种物料拼接部分效果图
实验表明,在相同实验环境下,传统TMA算法和GPT优化TMA算法拼接效果不佳,存在拼接错位现象;错位现象的出现容易将1个物料判断为多个,从而导致物料计数错误。本文算法能够较好地拼接出物料全景图,不存在错位现象,具有较好的拼接效果。
4.3 实验分析
4.3.1 系统稳定性验证
为了验证本文算法的高效稳定性,本文以主频2.1 GHz,内存8 GB的处理器为系统实验环境。选取安全带插片、大蒜以及小铲子3种物料,其中安全带插片450个,大蒜235个,小铲子538个。采集大小为1 344×87的物料图像进行处理,通过其他两种算法以及本文算法对物料进行检测,其检测结果见表2。
由表2可知,本文算法对物料数量检测的准确度达到97.36%以上,表明,本文算法对于物料计数的检测具有准确度高,可靠性好的优点。

表2 物料检测结果
4.3.2 物料计数准确度对比
由于传统TMA算法和GPT优化TMA算法在进行拼接时精度较低,出现的错位情况较多,导致计数准确度不高。
本文算法与传统TMA算法相比,计数准确度由77.32%提高到97.36%以上,与GPT优化TMA算法相比,计数准确度由84.94%提高到97.36%以上,由此可知通过本文算法进行处理,物料的计数准确度得到有效提升。
4.3.3 物料拼接时间对比
3种不同算法的物料拼接时间对比结果如表3所示。由表3可知,本文算法与传统TMA算法相比,处理一张样本图片的平均时间由0.013 s缩短为0.008 s,与GPT优化TMA算法相比,处理一张样本图片的平均时间由0.011 s缩短为0.008 s。由此可知,本文算法有效减少了物料拼接时间,提高了物料计数检测效率。

表3 3种算法拼接时间对比结果
4.3.4 拼接精度对比
方根误差(RMSE)可用于比较不同模型在同一数据集上的预测表现。拼接误差越大均方根误差越大,本文采用均方根误差来衡量拼接结果的精度[24]。3种算法拼接后图像均方根误差对比结果见图5。由图5可知,对于3种物料,采用本文算法拼接后的图像均方根误差较小,即错位情况较少;因此本文算法的拼接精度高,可以克服传统算法的缺点,大幅度减少图像拼接的错位情况,避免物料计数错误。

图5 3种算法均方根误差对比结果
5 结 论
本文提出了一种基于双模板搜索和位置约束系数的改进模板匹配物料计数算法。通过对改进的模板匹配算法进行稳定性检测以及与其他两种算法的检测结果进行对比,验证本文算法在检测时间、拼接精度以及计数准确度等方面都得到了有效的提高;实验中存在的误差可能是因为在进行物料图像采集时,存在物料大面积粘连的情况,需要进一步改进硬件设备并且进行更深入的算法研究。实验证明了改进的模板匹配算法具有稳定性好、准确性高和检测速度快的特点,可以满足工业生产中物料计数的要求。
