地下通道暗挖施工对上部既有管线的影响研究

冯兴法 向 昭

（1.重庆交通大学河海学院，重庆 400042；2.中煤科工重庆设计研究院（集团）有限公司，重庆 400042）

0 引言

随着城市经济的快速发展，人口的迅速增多，环境与交通问题向人们提出了严峻的挑战。在城市的主要街道上横穿道路修建地下过街通道是改善城市的交通状况、方便行人、减少交通事故的有效途径之一。修建地下过街通道，工程量小，施工工期短，可以较快投入使用［1］。近年来，在各大城市修建了很多地下过街通道，已经取得了很好的经济效益和社会效益，同时也积累了宝贵的施工经验。地下过街通道的施工方法主要有明挖法、盖挖法和暗挖法等。其中由于暗挖施工可保证修建过程中不中断交通，所以它成为修建城市地下过街通道首选的一种施工方法。本文对应用暗挖法成功修建地下过街通道的实例进行分析介绍，为类似工程中既有管线安全评估提供参考。

1 理论计算模型

本文主要研究暗挖工程与既有管线垂直相交时对既有管线的影响。地下工程暗挖施工过程中，将其上部的既有管线受力区域划分为CD段开挖区域，BC、DE段开挖引起的土体松动段，AB、EF段为开挖未影响区域，如图1所示。埋地管道所受到的最大荷载主要来自于其上部土体重力，对埋地管道竖向土压力的计算用的是太沙基筒仓计算模型。其指出土体颗粒相互错动产生应力传递，使得周围土体对下移土体产生一定的制约作用，导致地下结构承受的竖向土压力小于土柱重力［2-3］。既有顶管未受开挖影响的AB、EF段均布荷载q1即可使用太沙基土压力计算模型进行计算；而开挖段及开挖影响段上方的土体受到施工扰动影响，土体力学性能降低，对下移部分的挟制能力降低，导致地下管线承受的土压力增加，理论模型中假设开挖段CD上部管线承受的土压力为q3，开挖影响段BC、DE上部管线承受的土压力为q2。

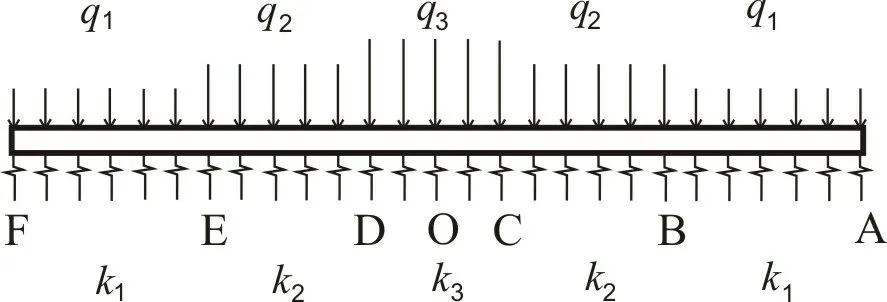
图1 暗挖影响下既有管道受力示意图

据图可得各段挠曲微分方程为：

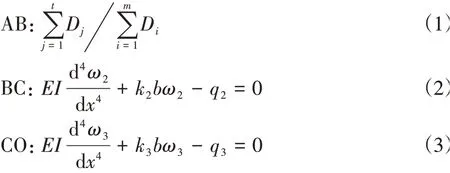
式中：

EI——既有管线的抗弯刚度，N∙m2；

ωi——既有管线各段的挠度，m，i=1，2，3；

x——既有管线右半段各点与O点的距离，m；

ki——既有管线下部各段地层的基床系数，N/m3，i=1，2，3；

qi——既有管线各段承受的土压力，Pa，i=1，2，3；

b——地基反力计算宽度，m。

根据地基反力计算宽度得到柔度特征值:

其中i=1，2，3。

则可得到各段挠曲微分方程的通解以及各段通解的一阶、二阶、三阶求导为:

若已知梁挠度，可得梁任意截面的转角，弯矩，剪力可用式（6）表示：

式中：

θ——既有管线的转角；

M——既有管线的弯矩，N∙m；

Q——既有管线的剪力，N。

实际施工情况下，管线长度较大，由于管周土体对既有管线的约束，管线下方的开挖对既有管线影响范围是有限的，在与开挖范围较远距离的端部（x→∞），可假设边界条件为固支。因此，可得到如下边界条件及变形协调条件：

A点（x→∞）为固定端：

O点为对称点：

根据B、C两点左右两端挠度、转角、弯矩及剪力的协调关系，可得如下补充条件：

B点：

C点：

把公式（7）~（10）代入公式（5）中，可得到一个12个方程的方程组，12个未知数。通过MATLAB编程，得到各待定系数Ai、Bi、Ci、Di的解析解，再分别代入（7）~（10）中，即可得出BC 段开挖时，既有管线AE 中各点产生的挠度、转角、弯矩和剪力，选取合适的判断标准，即可评估既有管线的安全性。

2 理论计算相关参数的确定

2.1 既有管道上垂直土压力计算

本文选用太沙基筒仓计算模型对未受开挖影响的既有管线竖向土压力q1进行计算。开挖段及开挖影响段上方的土体受到施工扰动影响，土体力学性能降低，对下移部分的挟制能力降低，导致地下管线承受的土压力增加［4-5］，基于简化计算以及偏于安全的考虑，本文采用土柱理论计算开挖段及开挖影响段上方既有顶管上覆土压力q2和q3。

2.2 暗挖施工影响段长度确定

隧道开挖引起的土体松动区域，假设土体松动线与开挖部分的底面水平线夹角为(45°-φ/2)，如图2，则可计算出松动段的长度为：

图2 松动段长度计算示意图

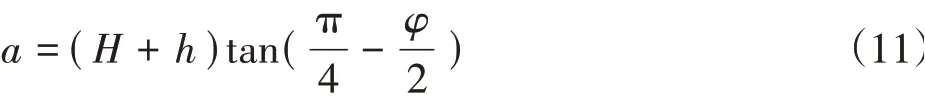
式中：

a——开挖影响段长度，m；

H——开挖区域顶部与既有管线的距离，m；

h——开挖区域的高度，m；

φ——土体的内摩擦角，°。

如图2所示，根据体应变将隧道开挖扰动分为三个区域，体应变大于3%为A区，体应变1%~3%为B区，体应变小于1%为C区。各区域变形模量改变幅度大于黏聚力和内摩擦角改变幅度，内摩擦角整体改变最小。A区各不同点变形模量降低37%~91.7%，黏聚力降低31.4%~63.7%，内摩擦角降低3.6%~12.3%；B区各不同点变形模量降低8.1%~24.1%，黏聚力降低2.5%~23.1%，内摩擦角降低1.1%~2.3%。

2.3 施工扰动影响下基床系数的确定

本文建立的理论模型中，基床系数为最重要的参数。地下通道暗挖施工，对既有管线周围的地层产生扰动，导致基床系数产生变化。在具体工程中，宜通过室内外试验确定原状土和施工扰动土基床系数［5］。基于既有文献，对暗挖区域上方（既有管线下方）地层进行暗挖扰动分区，见图3。然后对各区域土体的平均变形模量、平均黏聚力以及平均内摩擦角等进行预估，根据常见力学参数的预估值计算施工扰动影响下的基床系数。

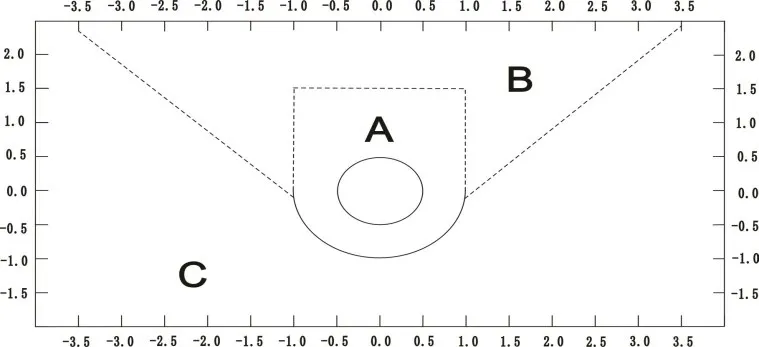
图3 隧道开挖扰动分区示意图

施工扰动下的基床系数根据变形模量和泊松比预估值进行计算。本文选择该方法进行施工扰动下基床系数的计算，公式如下：

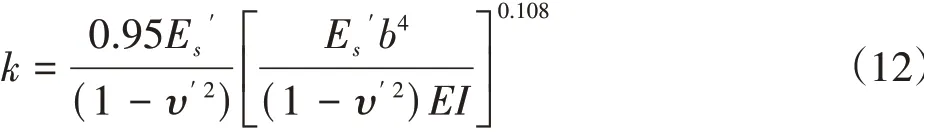
式中：

Esi——既有管线下部各段土体的变形模量，Pa；

υi——既有管线下部各段土体的泊松比；

泊松比可根据各段土体的侧压力系数k0i计算得到：

侧压力系数可由三轴剪力仪或侧压仪测量，由经验公式确定：

3 案例计算与分析

武汉卓刀泉地下人行通道，埋深3m，净宽8m，净高3.55m。地下通道上覆土主要为粉质黏土，黏聚力为15kPa，内摩擦角为12°，重度为19.3kN/m3，基床系数为1.4×104kN/m3。地下通道上方有一DN100铸铁管，管道外径114mm，埋深1.5m。按本文方法通过对基床系数多次取值试算，得出开挖段和开挖影响段不同基床系数取值下既有管线沉降槽,与现场实测沉降槽对比情况如图4所示。

图4 基床系数计算沉降量与实测值对比

分析得出如下结论：

（1）当开挖段基床系数取值为原始基床系数10%，开挖影响段基床系数取值为原始基床系数30%时，计算沉降曲线与实测沉降曲线吻合最好（图中计算值1与实测值代表的曲线）。具体表现为：①最大沉降量均发生在暗挖断面的中点位置，计算值稍大于实测值；②计算与实测的沉降槽左右两侧的宽度均为12m左右；③各测点的实测数据与计算值相差均较小，特别是沉降极大的区域，计算值均稍大于实测值，符合预测值宜偏于安全的工程要求。④两条曲线存在的差异为：在距离暗挖断面中点6~9m区间内，计算沉降有轻微的增加趋势，而实测值持续呈减小趋势。分析其具体原因如下：开挖影响段基床系数取值为原始基床系数的30%，但在实际工程中，开挖影响段的基床系数不是某一定量，距离开挖段近的部分受到扰动更大，基床系数更小，而距离远的部分，基床系数更大。基床系数取值越大，则计算沉降量越小。计算沉降槽与实测沉降槽曲线的差异，表明距离开挖段近的开挖影响段前半段的基床系数取值（0.3k1）偏大，导致前半段计算沉降量偏小。

（2）多次试算结果表明，开挖段的基床系数是计算中最关键的取值参数，直接影响最大沉降量及沉降极大区域（距离暗挖断面中点0~3m区间）的沉降计算结果。本案例中，开挖段基床系数比适用值（0.1k1）小25%时，计算最大沉降值增加35%，开挖段基床系数比适用值（0.1k1）大25%时，计算最大沉降值增加20%。由此可见，该参数的取值对计算结果影响很大，直接关系到预测评估的准确性。因此，在有条件的情况下，尽量使用室内外试验确定开挖段基床系数。

（3）多次试算结果表明，开挖影响段的基床系数对最大沉降量几乎无影响，对沉降极大区域（距离暗挖断面中点0~3m区间）的沉降计算结果影响较小，对沉降次大区域（距离暗挖断面中点3~9m区间）的沉降计算结果影响相对较大。以本案例为例，若开挖段基床系数取值准确，开挖影响段的基床系数取值（相对于0.3k1）增加或降低30%，最大沉降量及沉降极大区域计算值差距较小，且均偏于安全，沉降次大区域计算值差距相对较大，但计算值绝对差值均小于2.5mm。总体而言，该参数适宜的取值区间相对较大，取值偏差在30%范围内，对管线沉降值计算结果影响较小。

4 结束语

地下暗挖工程下穿既有管线施工过程中，管线下方地层受到不同程度的扰动，基床系数存在较大差异。基于Winkler弹性地基梁理论，考虑既有管线下方各区域土体基床系数的差异，建立了暗挖施工对上部既有管线影响的理论计算模型，提出了施工扰动影响下的基床系数等相关参数的取值方法。使用理论模型对暗挖影响下既有管线沉降量进行了计算，并与实测沉降量进行了对比。计算结果表明，开挖段的基床系数是计算中最关键的取值参数，其取值对计算结果影响很大；开挖影响段的基床系数，适宜的取值区间相对较大，对计算结果影响较小；各段基床系数取值适当时，计算沉降曲线与实测沉降曲线吻合良好。