混凝土弹塑性损伤本构研究
2022-08-23孙帆
孙 帆
(华南理工大学土木与交通学院,广东 广州 510641)
0 引言
混凝土本构研究在混凝土众多研究中属于基础性研究,其揭示了混凝土的破坏本质和机理,从早期线弹性胡克定律,到后来塑性力学的发展,再后来断裂力学以及损伤力学的不断壮大,这是不断揭示混凝土本质属性的过程。
就混凝土弹塑性损伤本构的发展来看,在此之前,大多学者研究了理想弹塑性本构以及弹性损伤本构,虽考虑了混凝土的塑性变形,但却未考虑损伤的发展。而弹性损伤本构则考虑了损伤,却也只限于弹性阶段。事实上,混凝土作为一个准脆性且非均匀材料,内部有着各种缺陷,在其进入塑性阶段必然也伴随着内部损伤的发展。同样的,损伤的发展必然也影响着混凝土的塑性变形,二者是相互耦合的关系。
本文在介绍混凝土弹塑性损伤理论发展态势的基础上,对近年来弹塑性损伤本构的理论和数值算法方面的发展进行了分析。
1 混凝土弹塑性损伤理论
混凝土弹塑性损伤理论的形成主要可以从以下两个角度分析:损伤变量的选取以及本构的演化规律。
损伤变量的选取经历了标量到双标量,再到张量的发展历程。由于混凝土的单边效应,为了更好地描述混凝土在受拉和受压下的不同行为,学者们将损伤变量进行分解,采用双标量。当混凝土出现裂缝或是要更加精确地描述其力学行为,则要考虑各向异性,那么损伤变量则表示为张量形式。张量的引进必然也使得问题分析更加地复杂化,实际的应用性也不强,故多标量形式的损伤变量在弹塑性损伤本构领域的发展仍然是最为经典的。
对于弹塑性损伤本构的演化规律,混凝土的卸载过程不仅包含刚度的退化,还会产生不可恢复的塑性变形,故同时考虑塑性变量和损伤变量是不可避免的。Mazars等[1]最早提出应力张量分解的思想,认为材料的受拉损伤只由拉应力所引起,而受压损伤只由压应力引起,尽管他们只考虑了弹性损伤,但这一损伤变量分解的思想却成为了弹塑性损伤理论史上的一座里程碑。Simo[2]等开发了采用不可逆热力学和内部状态变量的连续弹塑性损伤模型,在应力空间内选择余能为能量势,奠定了损伤理论的热力学基础。Faria等[3]在有效应力空间对应力张量进行正负分解,并利用有效应力定义了Helmholtz自由能,提出了双标量的弹塑性损伤本构。Resende[4]提出拉剪损伤本构模型,他认为材料的受拉损伤是拉伸损伤机制引起的,受压损伤是剪切损伤机制所造成的。
2 经典双标量弹塑性损伤本构模型
针对混凝土的非线性行为,更准确的描述在于如何更好地描述出混凝土的塑性以及损伤。这里介绍一种弹塑性损伤本构模型,该本构中采用了拉剪损伤机制,采用拉伸损伤变量和剪切损伤变量对混凝土的劣化进行描述,并且对应力张量在有效应力空间进行了正负分解[5]。
2.1 损伤机理以及应力-应变本构
在有效应力空间中定义无损条件下的有效应力,其服从经典的弹塑性模型,由应变等效原理,可知:

式中:
C0——混凝土的初始刚度,是个四阶张量;
εe、εp——混凝土的弹性应变和塑性应变。
其关系可表示为:ε = εe+ εp。再对有效应力张量进行正负分解:

式中:
p+、p-——均为四阶对称张量,分别表示为σˉ的正负投影张量。
相应的便可得知弹性Helmholtz自由能可以表示为

式中:

通过以上的弹性Helmholtz自由能定义,同样可类比定义塑性的Helmholtz自由能,一般认为二者是不耦合的。根据热力学第二定律,材料的损伤过程和塑性流动过程都是不可逆热力学过程,因此等温纯力学过程必须满足热力学不可逆条件,即能量耗散不等式:

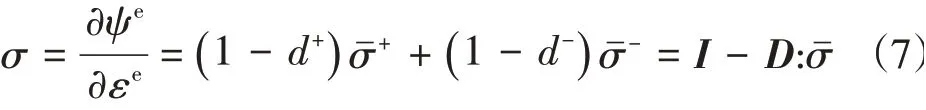
式中:
D——四阶对称张量。
不难看出,通过不可逆热力学推导出的应力-应变本构公式与损伤力学基础理论的在有效应力空间的推导结果是一致的。
2.2 塑性变形
首先在有效应力空间给出了屈服准则、非相关流动准则以及硬化法则,如下式:

式中:
F——塑性屈服函数;
FP——塑性势函数;
κ——硬化参数向量;
λ̇P——塑性流动因子,表示塑性流动的大小,为非负标量;
H——硬化函数向量。
上式准则还需满足加卸载规则即Kuhn-Tucker条件的限制,即:
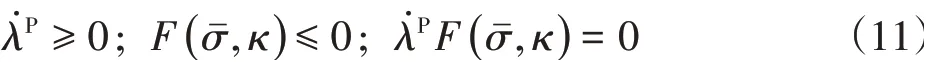
根据一致性条件,即可得出λ̇P的具体表达式。对于塑性屈服函数F以及塑性势函数FP,采用Lee等[6]给出的模型表达式,分别为:


式中:
α——反映双轴受力与单轴受力的关系;
Iˉ1和Jˉ2——分别表示有效应力张量的第一不变量和第二不变偏量;
c和β——分别是硬化参数向量κ的函数;
σˉmax——σˉ的最大有效主应力。
然而对于硬化向量函数H的表示,可以将硬化参量向量κ分解为单轴受拉以及单轴受压应力状态下的累积塑性变形,从而确定其演化法则,并推出硬化向量函数H的表达式,这里不再赘述。
2.3 损伤准则及演化法则
类比弹性Helmholtz 自由能进而可得到塑性Helmholtz自由能的表达式,二者均考虑了拉剪损伤机制的不同而采用正负分解形式以及无损的初始自由能形式。但值得注意的是,无损的塑性Helmholtz自由能与无损的弹性Helmholtz自由能表达上有所区别,主要由于材料的塑性阶段为非线性阶段,故应变能需要用积分的形式来表示,即:

考虑到试验中受拉状态下混凝土表现出明显的脆性,相比于受压时的塑性变形来说,受拉时的塑性变形可以忽略。因此,为了模型的简洁且便于计算,令:
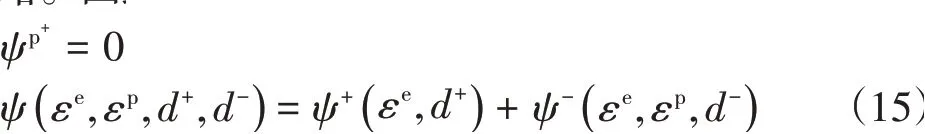
其中,材料的Helmholtz自由能的正负分量又可以表示为:

式中:
b0——材料参数。
为简化计算,受拉损伤能释放率和受剪损伤能释放率等效地表述为:
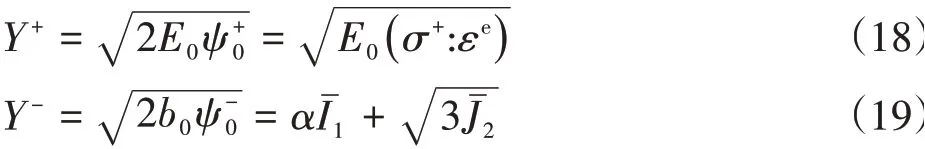
根据热力学第二定律的能量耗散不等式可以得出Y≥0,可认为当损伤能释放率达到一定阈值时,材料开始进入损伤阶段,由此给出损伤准则:

式中:
g±(x)——变量x的任意递增的标量函数;
r±——损伤能释放率的阈值,其控制着损伤面的发展,也指历史最大损伤能释放率。
令G=0,便可得到损伤面,根据损伤的正交流动的概念,从而可得到损伤变量的演化法则,即:

上述式子还需满足加卸载规则,即Kuhn-Tucker条件的限制:

当处于损伤加载时,G±= 0,再由一致性条件Ġ±= 0可以求出λ̇d±,得:

进一步可得:
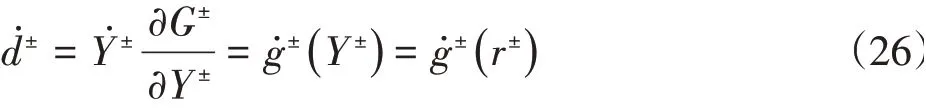

因此,只要给出损伤能释放率的函数g±(r±),就能得出损伤变量的演化法则的具体形式。然而这又是回到了损伤力学的的核心问题,也就是损伤变量如何演化。Faria等[3]对此做出了大量研究,并给出了损伤变量d±与损伤能释放率阈值r±之间的关系式,再由实验确定了参数。不难看出该模型损伤准则以及损伤变量演化法则的确立受到了塑性力学理论的启发。类比塑性力学的理论,塑性屈服函数以及塑性势函数即对应损伤本构中的损伤准则以及损伤演化法则,由于损伤变量采用正交流动法则,故不引用势函数。
3 弹塑性损伤本构的发展
理论上的创新完善主要由于复杂的工程条件以及复杂的加载方式的需要,例如耦合了冻融循环、高温作用这些物理场。简单运用经典本构模型必然不能反映材料的真实情况。又或是需要反映混凝土的一些特殊情况下的特性,诸如率敏感性以及各向异性等,就需要更加复杂和高级的本构模型。
在实际工程中,反复荷载加载十分常见,例如地震作用。这类动力作用使得混凝土表现出与静力作用下不同的特性,主要体现在率敏感性,具体表现为其动力作用下的强度和刚度受到应变率的影响。吴建营等[8]受到塑性流动法则中对塑性流动因子进行黏塑性规则化的启发,从而对损伤能释放率阈值的Perzyna黏性规则化,将混凝土静力弹塑性损伤本构模型进行了动力推广,并提出统一的一类基于能量的弹塑性损伤本构模型。
Voyiadjis等[9]在热力学一致的弹塑性损伤理论的框架内提出了一种混凝土材料模型。采用两个各向异性损伤张量和两个损伤判据来描述在拉伸和压缩载荷下混凝土力学性能的显着下降。总应力张量被分解为拉伸和压缩分量,以适应对上述破坏张量的需求。在这项工作中提出的塑性屈服准则解释了应力张量的频谱分解,并允许使用多个硬化规则。
李杰等[10]基于对混凝土构成性质的随机性与受力行为非线性的认识,对混凝土本构关系与结构非线性分析方法进行了系统的研究,形成了混凝土随机损伤力学的理论体系。对于细、微观层次损伤的概率性刻画,不仅可以解释损伤赖以产生和发展的物理机制,也可以建立损伤演化从细观到宏观的桥梁。
4 结束语
纵观弹塑性损伤本构的发展史,从开始的弹性损伤,逐渐不能满足混凝土工程实际应用的要求,慢慢发展到塑性损伤,到后来随着实际工程应用的复杂性,不断对基本理论进行创新,考虑多物理场的耦合,考虑动力效应等。再到后来从细观角度研究其本构,加入了随机性,或许在不久的将来,会在粒子的角度来研究混凝土本构。可见,混凝土本构研究作为一个基础研究领域,随着各学科的不断发展融合,必然会使混凝土本构研究与时俱进,更为精细化。
