微观交通仿真模型参数标定发展与优化实证研究

单籽跃， 周晨静， 韦昌永， 高亚聪

(1.北京建筑大学 通用航空技术北京实验室， 北京 100044； 2.北京未来城市设计高新尖创新中心， 北京 100044；3.广西壮族自治区高速公路发展中心， 南宁 530028； 4.北京工业大学， 北京 100124)

1 微观交通仿真模型参数标定发展历程

微观交通仿真技术是基于人、车单元的运行规律推演复杂交通系统的计算机模拟技术[1]，广泛应用于交通系统中复杂场景的人车交互问题[2]. 然而，现实交通场景是一个多因素相互作用的复杂系统，车辆运动行为特性也随着场景中道路条件、交通条件、管控条件及环境条件变化而相应调整，以保证车辆行驶的安全性、舒适性和高效性. 微观车辆运动模型均需要调整其内部参数才能反映特定条件下的交通流状况，这一调整过程即为模型参数标定，根据实地的交通运行状况对模型中各独立参数进行调整以使模型能准确表达具体仿真对象.

自20世纪90年代仿真技术应用于交通系统研究，微观仿真模型标定方法也不断推进及完善. 1991年Benekohal[3]建立微观交通仿真模型参数校正和验证工作框架，包括定义研究目标、确定实测数据、选择影响因素水平、建立评价标准、构建仿真网络、确定行驶路径、模型输出结果评价. 其后研究者根据自身实践工作经验在该框架基础上改进形成更为详尽可行的参数标定流程. 具有代表性的包括：①Helinga[4]于1998年阐述的仿真校正工作内容分为3部分. 首先是前期分析准备，包括定义校正目标和对象、确定所需原始数据、选取效能评价指标、简历评价检验标准；第2部分是仿真模型初始化校正，包括网络物理建模准确性检验、驾驶路径选择行为特性检验、OD分布特性检验及宏观交通流表现分析等；第3部分是分析结果评价，即为模型输出结果评价和验证. 当输出结果达不到验证标准时，需要重新开展校验工作，通过逐次调整仿真参数来确保最终校正模型满足误差要求. ②Hourdakis[5]和J.D.Schneeberger[6]在Hellinga的所列仿真校正工作内容的基础上，于2003年提出仿真模型标定9步校正流程(如图1(a)所示). ③Ciuffo[7]于2007年总结出的微观仿真标定整体流程，包括确定性能评价指标、进行模型敏感性分析、选取优化算法、确定目标函数、依据优化算法进行参数寻优、进行敏感性验证(如图1(b)所示). 3种代表性工作的提出与交通流理论及其他相关学科发展有着密切关系：随着交通流系统研究的深入，交通研究工作者逐渐认识到道路交通流系统的非线性变化及影响因素的多样性；由于仿真参数较多，先前模型参数标定工作较多应用实验设计方法(正交实验法、拉丁方格法等)，为减少仿真校核工作量，常选取具有代表性的参数组合进行仿真模拟；随着智能优化技术的发展(蚁群算法、遗传算法[8-9]等)，仿真参数标定工作可开展全样本量参数组合系统性寻优，避免了传统实验方法中以偏概全的不足.

国内微观交通仿真技术发展及应用由北京工业大学荣建教授于1999年开发完成第1个高速公路仿真软件BESS开始，微观仿真标定工作也取得了一定研究及应用进展. 代表性工作有：荣建、马建明等[10]最早利用交通仿真模型分析交通设施通行能力，提出高速公路基本路段仿真总体框架，包括模型标定，并经实测数据对模型标定、验证，证实流量—速度—密度关系与实际误差很小；张智勇[11]利用车载高精度GPS定位跟踪技术采集实际交通流跟驰特性数据，标定CA跟车模型；孙剑[12]在Hellinga提出仿真标定工作框架的基础上，于2004年在国内首先提出微观仿真标定工作流程(如图2)，并用拉丁方格法进行试验设计，对vissim的仿真参数进行校正. 王晓原[13]运用五轮仪实验系统获取实际车辆数据包括前后车速度、位置及加速度，对测量跟驰模型的运行指标进行参数标定；李志明[14]等于2006年在国内应用遗传算法开展基于VISSIM仿真平台的模型参数标定工作. 至此我国微观仿真模型标定工作进入优化算法应用阶段，具体工作如表1所示.

与国外发展类似，国内微观仿真模型标定工作经历了以车辆运动记录设备记录车辆驾驶参数的拟合发展阶段、以实验设计方法为基础的匹配校正发展阶段和以智能优化算法为基础的寻优校正发展阶段. 在参数拟合发展阶段需要采集大量微观驾驶行为数据，耗费大量的人力及物力资源，但是仿真参数标定结果具有实际具体含义；匹配校正及寻优校正阶段，采用实验设计方法或智能优化算法，反向选取符合校核目标函数的参数组合，大多数工作可在室内完成，尤其是寻优校正阶段可通过编程语言实现自动化校正，节省大量人力物力. 然而由于后2个阶段本质上是一个非线性优化过程，最优值可有多个，且大多数最优值也存在无法合理解释其物理含义的缺点，致使微观交通仿真模型标定结果存在难以移植、可信度低等缺点[25].

2 微观交通仿真模型参数标定优化与验证

2.1 基本优化思路

为提升微观交通仿真模型参数标定结果可移植性与可信度，团队在以往研究的基础上依据参数特性开展精细划分工作，具体从参数分类和参数取值2个方面进行优化：

2.1.1 参数分类

区别于以往对参数全样本智能寻优标定，将微观仿真模型参数分归为2类，全局参数与局部参数，其中全局参数为影响整体车辆运行的参数，表征车辆驾驶舒适性和高效性，如期望速度、最大加(减)速度、可接受加(减)速度、加速度与车速基本关系特征等；局部参数为车辆实现换道、跟车、让行等行为的控制参数，表征车辆驾驶安全性. 提出全局参数工程实测确定，局部参数智能寻优标定工作思路[26].

表1 近年我国微观仿真模型参数标定工作内容

图1 国外微观仿真模型标定流程

图2 我国微观仿真模型标定流程

2.1.2 参数取值

针对智能寻优算法可获取多组不同分布形态的参数优化结果，建议对结果进行聚类筛选，以数据集中程度为判定依据逐步提炼结果取值，提出基于信息熵判定的聚类递归取均值的结果获取方法[27].

由此，依据以上优化思路可形成参数整体标定且参数结果整体取均值、参数分类标定且参数结果整体取均值、参数整体标定且参数结果递归分类取均值、参数分类标定且参数结果递归分类取均值4种组合方案. 本次研究拟应用仿真实验实证各个方案的有效性.

2.2 实证方案设计

本次研究选用VISSIM平台，以信号交叉口为对象证实优化方法的有效性，设计4种实验方案与实测值、默认参数条件下仿真获取的延误、排队长度、通过流量等结果进行对比研究：

方案1 参数分类标定，结果整体取均值；

方案2 参数分类标定，结果聚类递归分类取均值；

方案3 参数整体标定，结果整体取均值；

方案4 参数整体标定，结果聚类递归分类取均值.

为实现“全局参数工程实测确定，局部参数智能寻优标定”的工作思路，团队通过以道路实车车辆的方法获取了车辆运行的最大加(减)速度、可接受加(减)速度及加速度与速度关系等指标[28-30]. 应用于VISSIM仿真平台，具体设置如表2、图3、图4所示.

表2 最大加、减速度取值对比 m·s-2

图3 模型默认期望加速度取值(左)与标定后取值(右)对比

图4 模型默认期望减速度取值(左)与标定后取值(右)对比

确定车均延误作为校核指标对VISSIM内部参数中12种局部参数开展参数敏感性分析[26]，最终选定平均停车距离(AX_average)、安全距离的附加项(BX_add)、安全距离的倍数项(BX_mult)和安全距离折减系数(ABX)4个参数为待标定局部参数，参数取值范围如表3所示.

表3 局部参数的种类及取值范围

利用智能寻优算法获取参数标定结果后，直接取均值即为结果整体取均值的操作. 同时以信息熵作为分析指标，对寻优后参数结果进行聚类递归分类取值具体操作如下：

1)假设第k类样本占当前样本集合D比例为pk(k=1,2,…|y|),则D的信息熵计算公式见式(1)：

(1)

2)根据规则得出Ent(D)的值越小，D的纯度越高，体现参数集中程度高，对校核指标影响较大.实现聚类取值方法，主要通过计算各参数信息熵，判断影响校核指标程度大的参数优先确定其参数最优值，去除其余解，对剩余参数信息熵重新计算，重复上述步骤，直至所有参数标定结束.

2.3 实测数据整理

选取北京市西大望路与广渠路信号交叉口作为实际场景，实测数据包括：

1)道路几何条件：车道宽度、车道数、车型比例；

2)交通条件：交通流量、期望速度、车均延误、排队长度、行程时间；

3)信号控制条件：配时方案、相位类型、次序和相位数. 采用视频拍摄法和人工计数法进行数据的采集. 选取工作日早高峰07:00—09:00，对该时间段内各进口道每5 min为间隔进行交通量的统计分析，如表4所示.

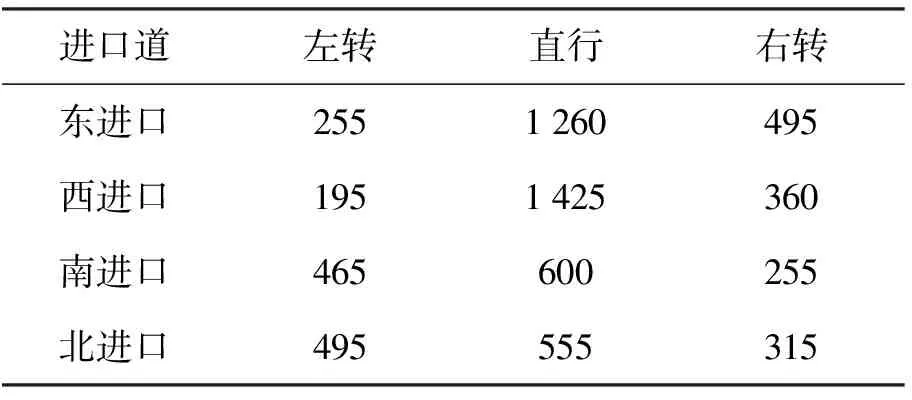
表4 各进口道小时交通量 pcu·h-1

信号交叉口内各车道宽均为3.5 m，信号周期时长为158 s，配时方案为四相位，信号交叉口实景与仿真图如图5所示，信号配时方案如图6所示.

图5 西大望路与广渠路信号交叉口

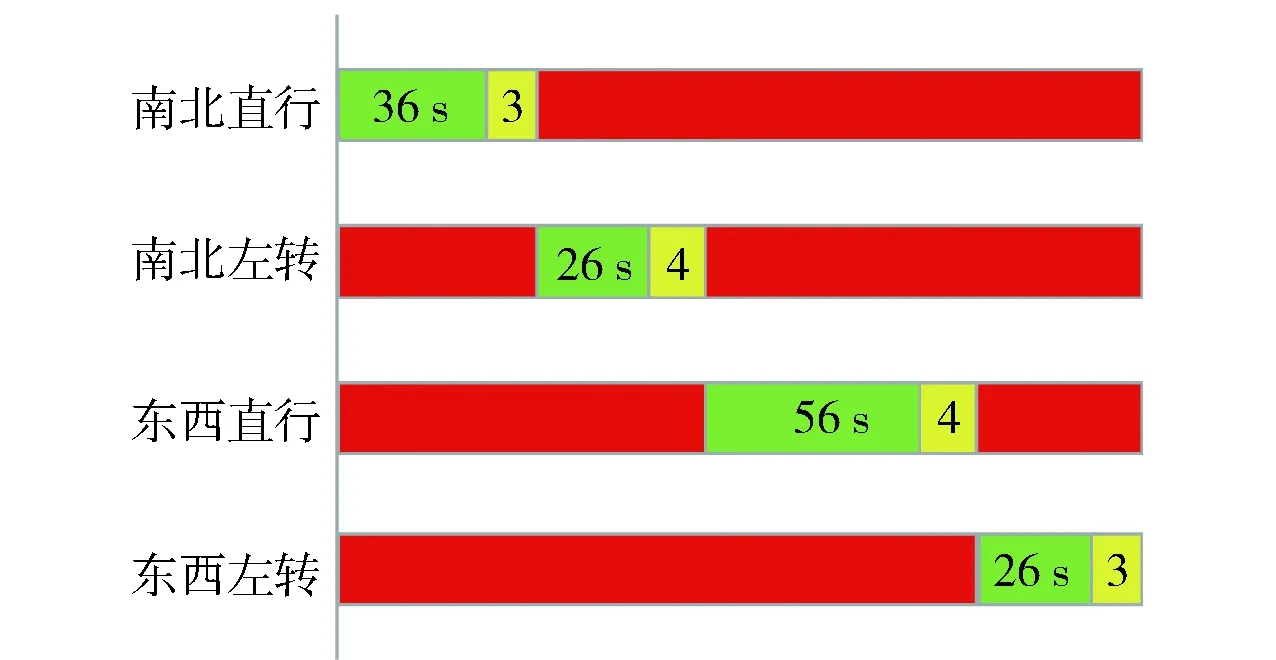
图6 西大望路与广渠路信号交叉口配时方案

2.4 仿真标定结果

选取遗传算法作为智能优化算法，基于VISSIM仿真软件外接程序COM接口，在VB语言编码下对4个待标定局部参数进行自动化迭代寻优工作，仿真参数标定实验共运行6 000次.

方案1和方案2(参数分类标定)满足上述确定分析方案原则的共有182种参数组合，而方案3和4(参数整体标定)得到170种参数组合. 方案1和方案3的各参数标定值通过直接对各参数组合方案取均值得到；而方案2和方案4需在此基础上，应用聚类递归分类取值思想确定各参数标定结果，即对各参数进行归一化处理，使各参数值均分布在(0,1)范围内，同时对各参数归一化结果进行聚类，聚类结果后各参数分布对比情况如图7～10所示.

图8 方案2(上)和方案4(下)参数BX_add标定结果分布对比图

图9 方案2(上)和方案4(下)参数BX_mult标定结果分布对比图

图10 方案2(上)和方案4(下)参数ABX标定结果分布对比图

按照式(1)分别计算方案2和方案4各参数数值分布的信息熵，计算结果如表5所示.

表5 各参数信息熵

以方案2为例展示各参数取值过程，以信息熵越小优先取值原则，先界定参数AX_average的标定结果，保留参数AX_average聚类分布情况中占比最大的子类1，取均值确定其参数的最终标定值. 同时，剔除其他子类(即子类2)参数组合数据，重新计算剩余的3个参数的信息熵，参考上述参数AX_average标定流程依次确定两方案的所有参数标定值. 得到4种实验方案种局部参数的最终标定值，如表6所示.

2.5 标定结果分析

根据表6中4种实验方案的参数最终标定值以及参数默认值分别开展VISSIM仿真实验，不同方法的仿真输出车均延误值与实测值的对比情况如图11所示.

根据参数集标定和参数寻优结果取值方法的不

表6 不同方法参数标定值

图11 不同方法车均延误值

同，交叉组合设计的4种方案，通过图11 可知各方案仿真模拟输出值与实际观测数据的对比，以及与默认值的关系. 其中，直接采取默认值进行仿真，与实测值相比误差最大. 其次，将方案1和方案3、方案2和方案4分别与实测值进行比较，发现第1组方案1明显比方案3更接近实测数据，数值上差异较大，这是由于控制参数取值方法不变，方案1采取参数分类标定方法，即优先标定全局参数，再对局部参数进行智能寻优标定，提升了标定工作的效能. 证明参数标定工作应考虑全局参数及不同场景下涉及到的局部参数的全面参数标定. 第2组方案2和方案4在数值上与实测值差异不显著，而表5中方案2信息熵值小于方案4对应数值，表明只标定局部参数方法的数值分布离散型大. 进一步说明参数标定工作若忽略全局参数的界定，存在一定的不合理性，造成模拟真实交通流特性更大的误差，间接验证参数分类标定工作的重要性.

通过图11可明显观测到4种方案中方案2与方案4与实测值最为接近，相比方案1和方案3与实测值差距在数值精度上更为精确，证明参数寻优结果采取聚类递归分类取值的方法效果显著，优于直接均值的方法.

因此，经过仿真实验本文设计的4种交叉组合方案定性、定量分析，推荐参数标定工作采取精细化分类，优先标定全局参数，再标定全局参数；参数寻优结果取值利用聚类递归分类思想，对多组最优解进行择优选取确定最终参数标定值.

对以上定性分析进一步验证其合理性，对4种方案中得到明显优化的2个方案，即方案2和方案4，选取排队长度、行程时间和流量作为交叉验证指标，进行交叉验证实验. 实验的仿真结果如图12～14所示.

图12 不同方案平均排队长度

图13 不同方案平均行程时间

图14 不同方案流量

通过以上3个验证指标的实验结果，得出以下显著发现，方案2所模拟的排队长度、行程时间和交通流量与方案4相比，均更接近于实测值，说明方案2模型仿真结果复现实际交通流车辆运行特性能力强. 因此，验证参数标定工作和参数结果取值中参数分类标定与参数分类取值2个方法最优，推荐仿真实验中推广.

3 结论与展望

微观交通仿真模型参数种类较多且各自作用范围不同，对参数进行精细化分析，提出针对性标定方法体现出具体问题具体分析的思想，理论上比粗放式统一标定效果更好. 本研究通过仿真实证的方法进一步证实精细化分类标定与取值的有效性. 同时，应用工程实测方法确定更多的微观交通仿真模型参数，在减少仿真模型参数标定种类和工作量的同时，也增加了微观仿真车辆运行与现场车辆运行的相似性，对于提升模型参数标定结果的可移植性十分必要.

在微观交通仿真模型参数标定流程逐步丰富的基础上，实测大量的交通流运行数据，开展实际标定工作以确定各类交通工程设施微观交通仿真模型参数取值库，是推进微观交通仿真技术的关键.