含风电配电网小干扰稳定性的影响因素及改善方法
2022-08-23张晶晶李盈含
姜 萌,曹 红,张晶晶,李盈含,张 蔚
(1.国网上海市电力公司青浦供电公司,上海 201799; 2.国网上海市电力公司松江供电公司,上海 201699)
随着环保意识的不断增强和化石燃料价格的不断上涨,促使风力发电需求旺盛。在世界范围内,特别是在中国、美国和欧洲等国家和地区,风力发电场正在极大地取代传统发电厂。然而,高比例的风电并网会给电网的稳定运行带来一定挑战。
双馈感应风机(Double Fed Induction Generator,简称DFIG)由于具有变速恒频运行、转换效率高等优点而被广泛应用[1]。含风电配电系统的小干扰稳定性受到风机变换器控制参数、风电渗透水平和风电场位置等因素的影响。柔性交流输电系统(Flexible AC Transmission Systems,简称FACTS)装置也会影响含DFIG电力系统的小干扰稳定性问题。国内外对风力发电稳定性和电力系统的小干扰稳定性已有研究,文献[2]研究了影响含直驱式永磁同步发电机风力发电系统小干扰稳定性的因素。文献[3-4]研究了高水平风电渗透、电力调度和风电场位置对含DFIG电力系统的影响。文献[5]研究了风电负载率对含风电配电系统小干扰稳定性的影响。现有研究缺乏对含DFIG配电网小干扰稳定性影响多角度因素研究。本文研究含DFIG风力发电配电网小干扰稳定性的影响因素,并提出通过电压调节参数、接入位置的选择、渗透率的调整以及静止无功补偿装置(Static Var Compensator,简称SVC)的使用来改善小干扰稳定性。
1 DFIG和SVC建模
在研究DFIG和SVC装置对配网系统的小干扰稳定性的影响时,DFIG和SVC模型的选择尤为重要,下面分别介绍典型的DFIG模型和SVC模型。
1.1 DFIG模型
典型DFIG定子与电网连接,转子通过脉冲宽度调制电压源逆变器(Pulse Width Modulation-Voltage Source Inventer,简称PWM-SVC)对系统供电。DFIG典型结构如图1所示。
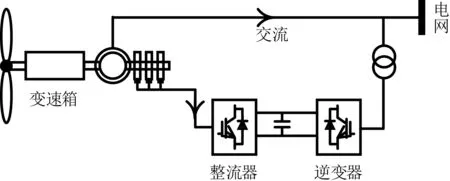
图1 DFIG典型结构图
1.1.1 动态特性
DFIG转子转速ωm、机械转矩Tm、电磁转矩Te计算公式如下:
(1)
Te=xm(iqriqs-idriqs)
(2)
(3)
式中Hm——等效惯性常数;ids,iqs——dq轴定子电流;idr,iqr——dq轴转子电流;Pω——输出机械功率。
Pω方程如下式:
(4)
式中ρ——空气密度;Cρ——风能利用系数;λ——叶尖速比;θp——桨距角;A——叶片扫风面积;vω——风速。
1.1.2 变换器
DFIG系统的变换器为脉冲宽度调制电压源逆变器(Pulse Width Modulation,简称PWM),变换器背靠背连接,由于其为机电暂态过程,方程式如下:
(5)
(6)
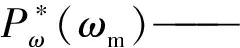
1.2 SVC模型
SVC是电力系统静止无功调节装置,可以调节系统节点电压等特定参数。SVC的稳态等值电路可等效为可变电纳[6],SVC模型等效总电抗bSVC计算公式如下:
(7)
式中Kr——稳定器时间常数;Verf——参考电压;V——母线电压;Tr——时间常数。
该SVC模型补偿的无功功率Q计算公式如下:
Q=-bSVCV2
(8)
2 仿真系统
采用IEEE-14配电网系统作为测试系统,该配网系统包括14条母线、2台同步发电机、3台同步补偿器、4台变压器和11处负载。IEEE-14配电网系统拓扑结构如图2所示。
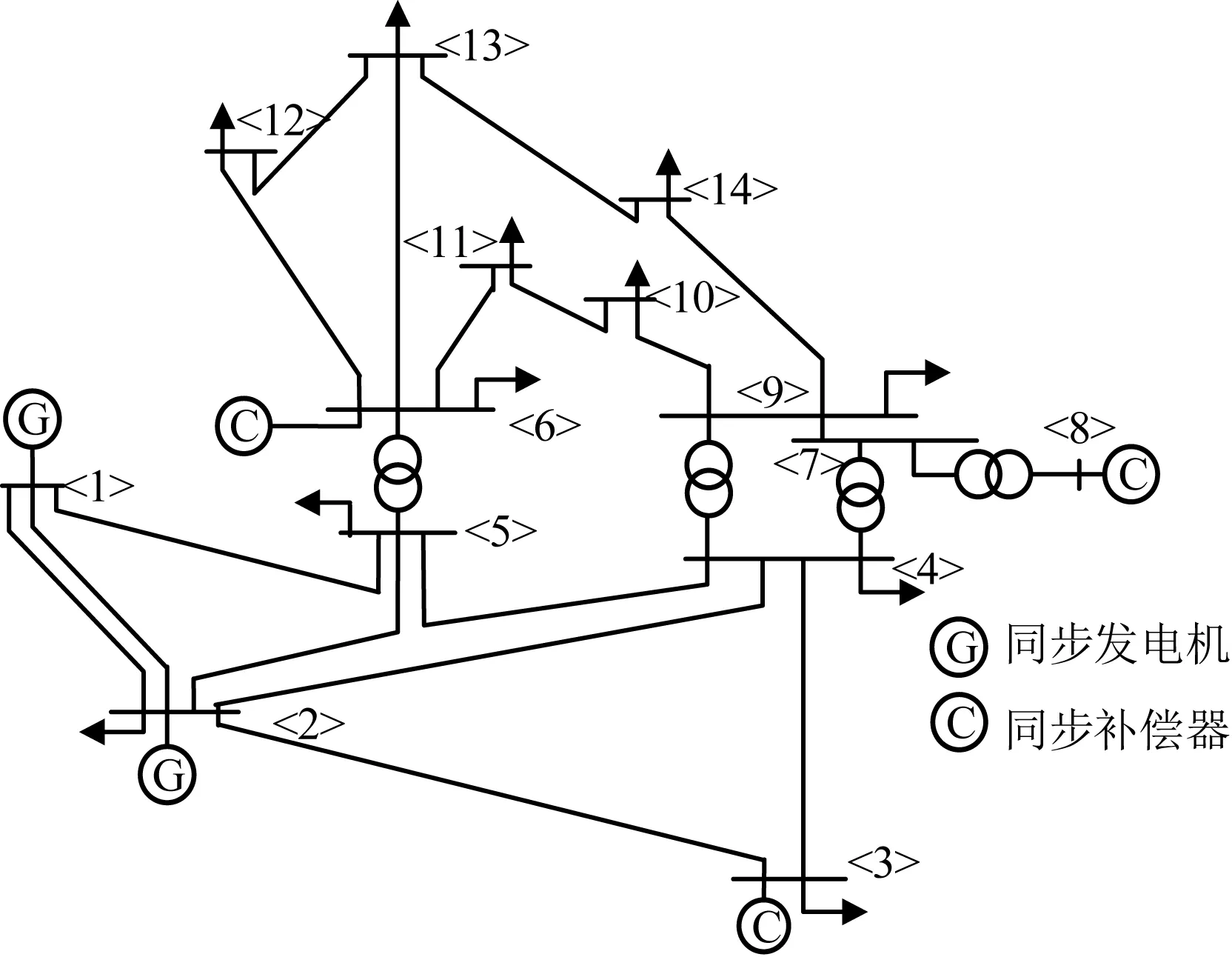
图2 IEEE-14配电网系统拓扑结构
3 仿真分析
变换器电压控制参数、渗透率、接入位置、FACTS装置等均会影响配电网小干扰稳定性。
3.1 终端电压控制参数对小干扰稳定性的影响
为了研究变换器电压控制参数Kv和功率控制时间常数T对所测系统小干扰稳定性的影响。采用控制变量法,保持一个参数,改变另一参数,研究电压控制参数及时间常数对系统稳定性的影响。
在IEEE14节点配电网系统中节点5处接入风机系统,风电渗透率为10%。分别研究DFIG风机系统在不同电压增益Kv和功率控制时间常数T下系统的不稳定振荡模态。研究表明系统共存在27组振荡模式,其中模式一变化明显且存在不稳定情况。DFIG风机系统在不同电压增益Kv下系统中模式一振荡模态变化情况如表1所示。
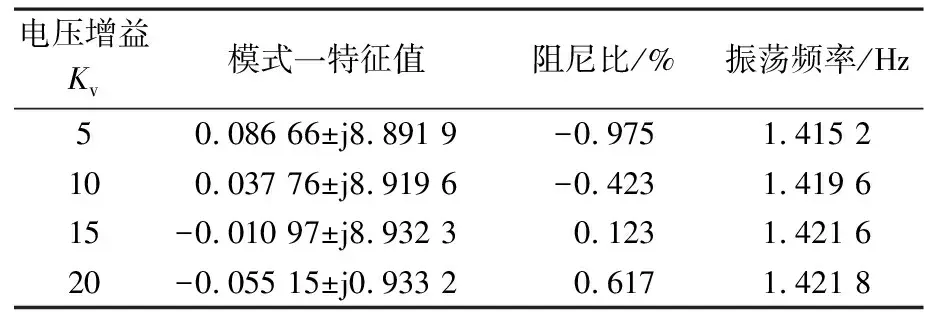
表1 电压控制增益对振荡模态的影响
从表1可以看出:当电压增益Kv为5和10时,系统存在一对正实部特征值,阻尼比为负数,表明电力系统在不稳定运行;当电压增益为15和20时,所有特征值变为负实部特征值,表明电力系统是稳定的。可见正实部特征值增加,不稳定振荡模式阻尼特性逐渐增强,电力系统小干扰稳定性增加。因此适当增大变换器电压增益,有助于系统的小干扰稳定性。
DFIG风机系统在15%渗透率下,不同功率控制时间常数T下的系统中不稳定振荡模态变化情况如表2所示。

表2 功率控制时间常数对振荡模态的影响
从表2可以看出:当时间常数T为0.01和0.1时,系统存在一对负实部特征值,阻尼比为正数,表明电力系统在稳定运行;时间常数T变为1和2时,模式一的特征值变为正实部特征值,表明电力系统是不稳定的。由此可见,随着功率控制时间常数T的不断增加,原本稳定的振荡模式阻尼特性逐渐减弱,电力系统小干扰稳定性变差。
3.2 渗透率对小干扰稳定性的影响
风电接入系统的渗透率不同,对系统小干扰稳定性的影响也不相同,通过研究不同渗透率下系统低频振荡模态可以分析风机系统容量对系统小干扰稳定性的影响。DFIG风机系统在电压增益Kv取10、时间常数T为0.01时,不同渗透率下的系统小干扰稳定特性如表3所示。
从表3可以看出:在渗透率为5%和10%时,系统存在一对正实部特征值,阻尼比为负数,表明电力系统在不稳定运行;在渗透率为15%和20%时,不稳定的特征值变为负实部特征值,表明电力系统趋于小干扰稳定;风电渗透率从5%增加到20%的过程中,不稳定振荡模式阻尼特性逐渐增强,系统小干扰趋于稳定。
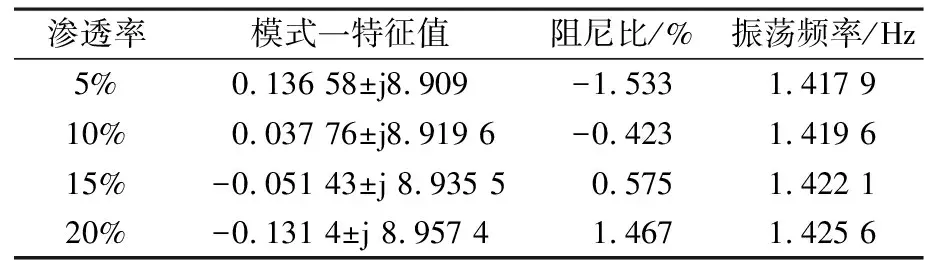
表3 风电渗透率对振荡模态的影响
3.3 接入位置对小干扰稳定性的影响
图3(a)和图3(b)为DFIG风电系统分别在节点5和节点14接入系统时,系统振荡模态的部分复特征根分布图。风机系统在节点5和节点14接入系统时,系统模式一的振荡模态变化情况如表4所示。

图3 风电接入节点5和节点14时系统振荡模式

表4 风电接入位置对振荡模态的影响
从图3和表4可以看出,风电场的位置显著影响电力系统的小干扰稳定性能。例如,当风力发电机连接到母线5时,振荡模式一变得不稳定;连接到母线14时,振荡模式一趋于稳定。
3.4 SVC装置对小干扰稳定性的影响
风电系统接入节点5,系统连接SVC装置时系统的振荡模态复特征根分布图如图4所示。含DFIG风电系统有无接入SVC装置时,系统模式一的振荡模态变电情况如表5所示。
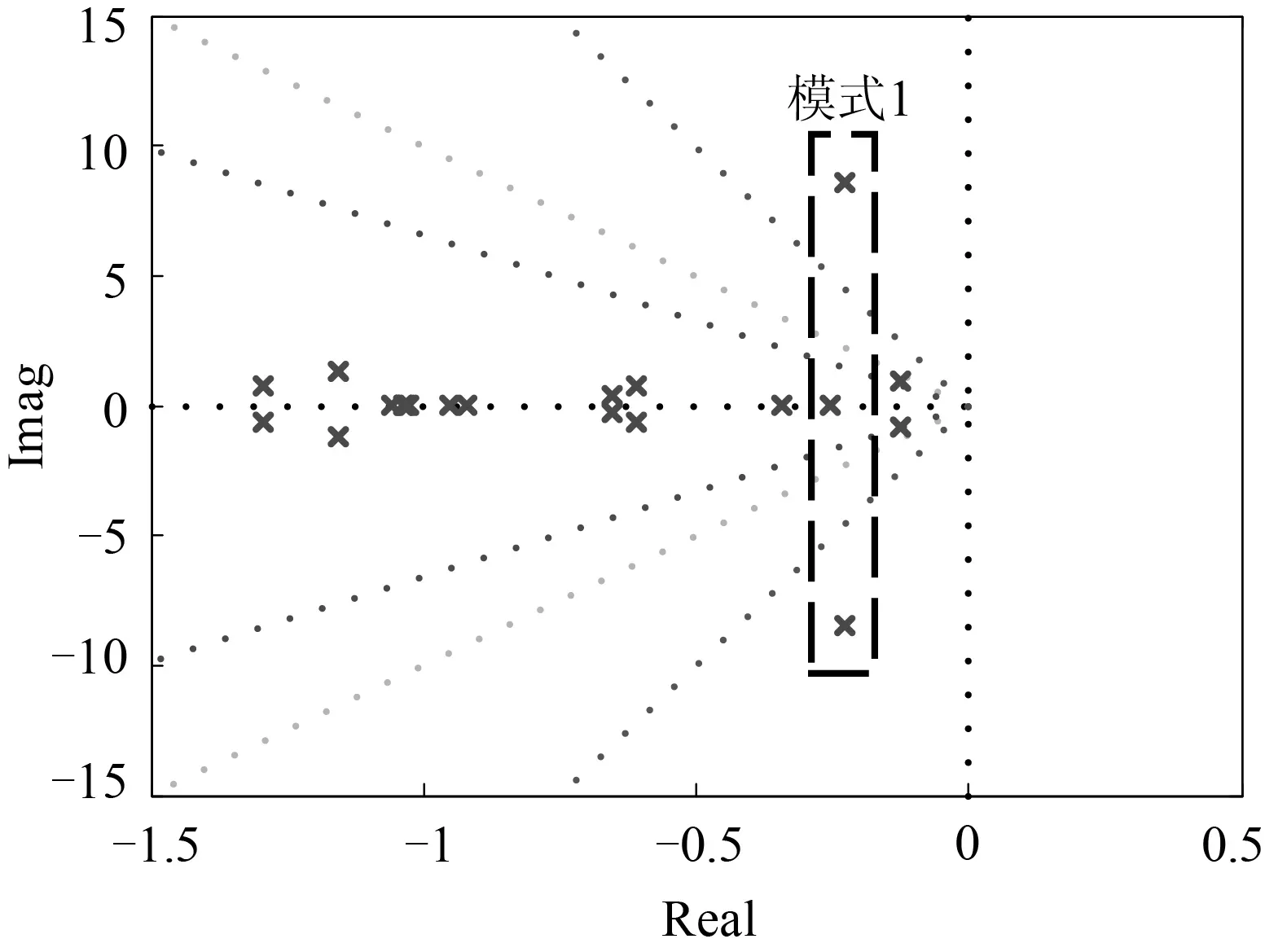
图4 接入SVC装置后系统振荡模式

表5 SVC装置对振荡模态的影响
从图4和表5可以看出:在10%的风电渗透率下,SVC装置投入运行后将振荡模式一的阻尼比从-0.423%提高到2.5%。一般来说,SVC装置对电力系统的小干扰稳定性有积极的效果,缓解了风力发电并网对配电网系统的不利影响。
4 结语
本文通过分析终端电压控制参数、不同风电渗透率、不同风机接入位置以及有无SVC装置接入等情况下含DFIG配电网系统的小干扰稳定性。
在风电渗透率为10%的情况下,增大电压控制有着积极的影响,而缓慢的功率控制会影响电力系统的动态性能。另一方面,风电场穿透水平和接入位置的不同也会影响系统的稳定性,使用SVC装置可以改善由于风电场穿透水平及其位置引起的小干扰稳定性问题。
