时变时滞多智能体系统的鲁棒二分一致性
2022-08-23陕雪琴裘哲勇胡鸿翔
陕雪琴,裘哲勇,胡鸿翔
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
多智能体系统是由多个相互连接的个体组成的一类复杂的动力系统,如:社交网络、智能电网等。近年来,多智能体的群集行为问题[1]引起众多领域专家学者的关注,多智能体系统实现有序群集行为的关键在于设计相应的分布式控制器。在网络拓扑结构中,个体之间不仅具有合作关系,还存在竞争关系,通常称这类网络为合作竞争网络。文献[2]首次研究合作竞争网络中一阶系统的二分一致性问题。进一步,文献[3]针对二阶多智能体系统,讨论了相应合作竞争网络的群集行为问题。上述研究均假设个体具体相同的动力学系统且是精确已知的,但这种假设在某些应用中受到限制。文献[4]研究具有异质匹配不确定项的多智能体系统的一致性问题,通过设计自适应分布式协议来保证一致性误差的有界性,文献[5]进一步推广了一类具有异质匹配不确定项的Lipschitz非线性多智能体系统的分布式鲁棒一致性问题。此外,在文献[4]的基础上,文献[6]将合作竞争网络引入多智能体系统,设计相应的鲁棒控制器使其在有无领导者情况下渐进实现二分一致性。本文针对具有异质匹配不确定项且具有内在非线性动力学的个体模型,设计了一类非连续静态分布式控制器,实现了整体系统的鲁棒二分一致性。
1 预备知识

(1)

D=diag(σ1,…,σN)
(2)
式中,当i∈K1,σi=1;当i∈K2,σi=-1。

引理1.2[8]对于任意给定的向量X,Y∈Rn和正定矩阵P∈Rn×n,有:
2XTY≤XTPX+YTP-1Y
2 带内部时滞的一阶个体模型
假设由N个个体所组成的多智能体系统,其个体动力学描述如下:
(3)
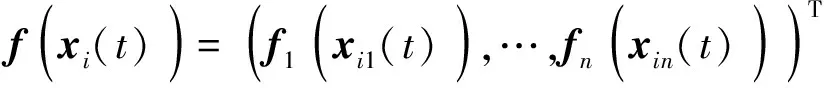
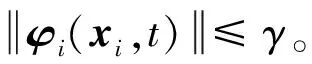

(4)
定义2.1对于任意的初始条件,若
(5)
成立,则系统实现了鲁棒二分一致性。
3 非连续静态分布式控制器
为了使带内部时滞的一阶个体模型实现鲁棒二分一致性,本文设计的非连续静态分布式控制器ui的具体形式如下:
(6)
式中,c1>0,c2>0表示标量控制增益,K表示反馈控制增益矩阵,sgn(·)表示符号函数,g(·)是一个非线性函数,定义如下:
(7)
将控制器代入状态方程,可得:
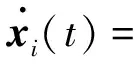
(8)
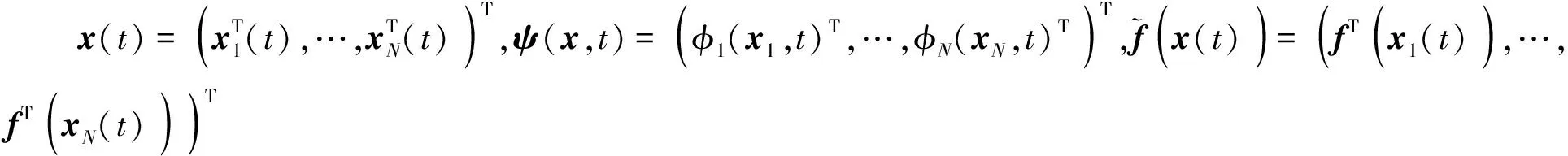
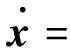
(9)
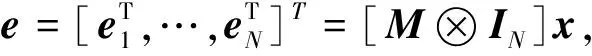
因此,可得鲁棒二分一致性误差的动力系统为:
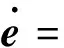
c2(M⊗F)G(e)+(M⊗F)ψ(x,t)
(10)
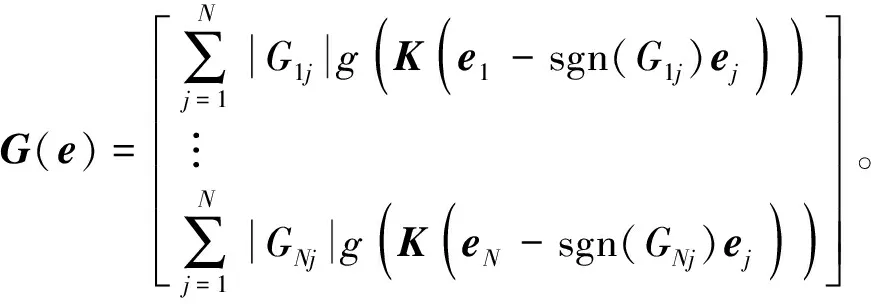
4 主要结果
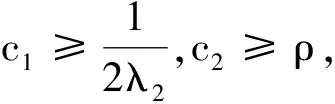
Δ2=s2IN-Q<0
成立,那么,满足非连续静态分布式控制器(6)的多智能体系统(3)渐进实现鲁棒二分一致性。
证明针对多智能体系统(3),构造Lyapunov函数如下:
V=V1+V2
(11)
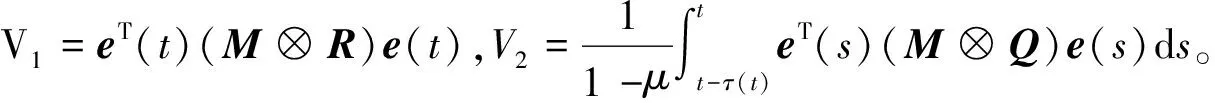
对函数V1求导,注意到M2=M,ML=L,K=-FTR,因此有:
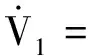
2c2eT(M⊗RF)G(e)+2eT(M⊗RF)ψ(x,t)
(12)
根据假设2.1,将式(12)中2eT(M⊗RF)ψ(x,t)进一步表示为:
(13)
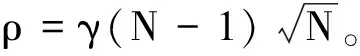
对于式(12)中2c2eT(M⊗RF)G(e),运用非线性函数g(·)的定义,可得:
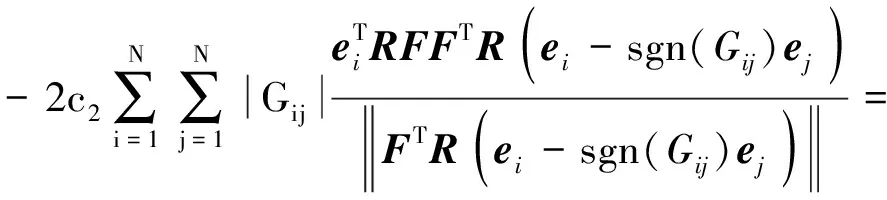
(14)
注意到c2≥ρ,将式(13)和式(14)代入式(12),式(12)进一步表示为:
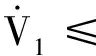
(15)
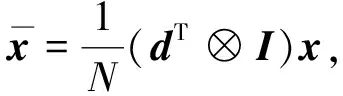

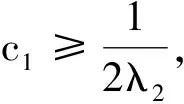
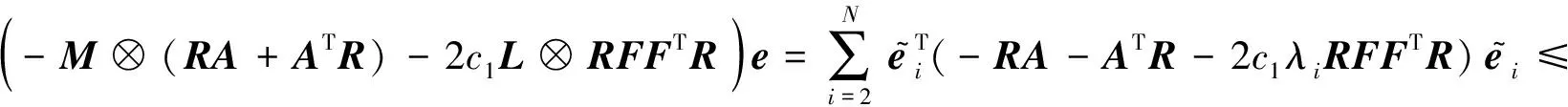
(16)
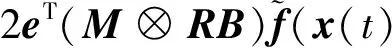
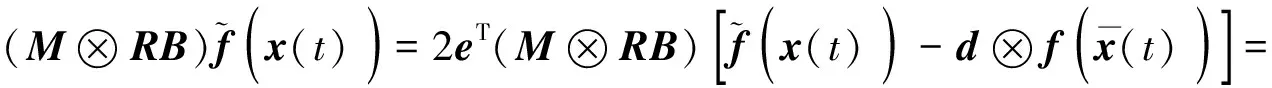
(17)
同理可得:
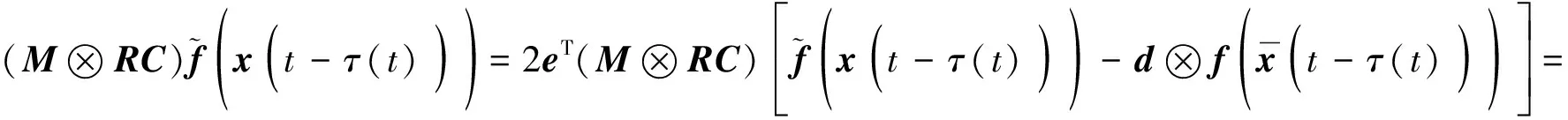
(18)
将式(16)—式(18)代入式(12),可得:
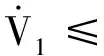
(19)

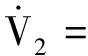
(20)
由式(11)、式(19)、式(20)可知:
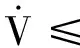
(21)
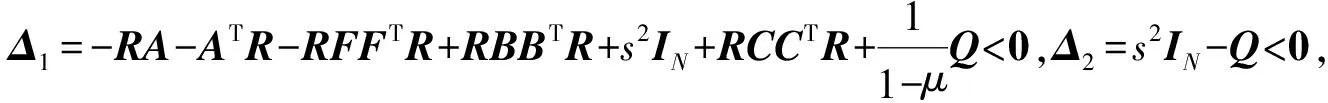
5 数值模拟与分析
5.1 仿真数据来源
假定由6个个体组成的合作竞争网络,其中个体1,2,3,5组成子集K1;个体4,6组成子集K2。网络拓扑结构如图1所示,其中实线边代表的权重为正,表示合作关系;虚线边代表的权重为负,表示竞争关系。
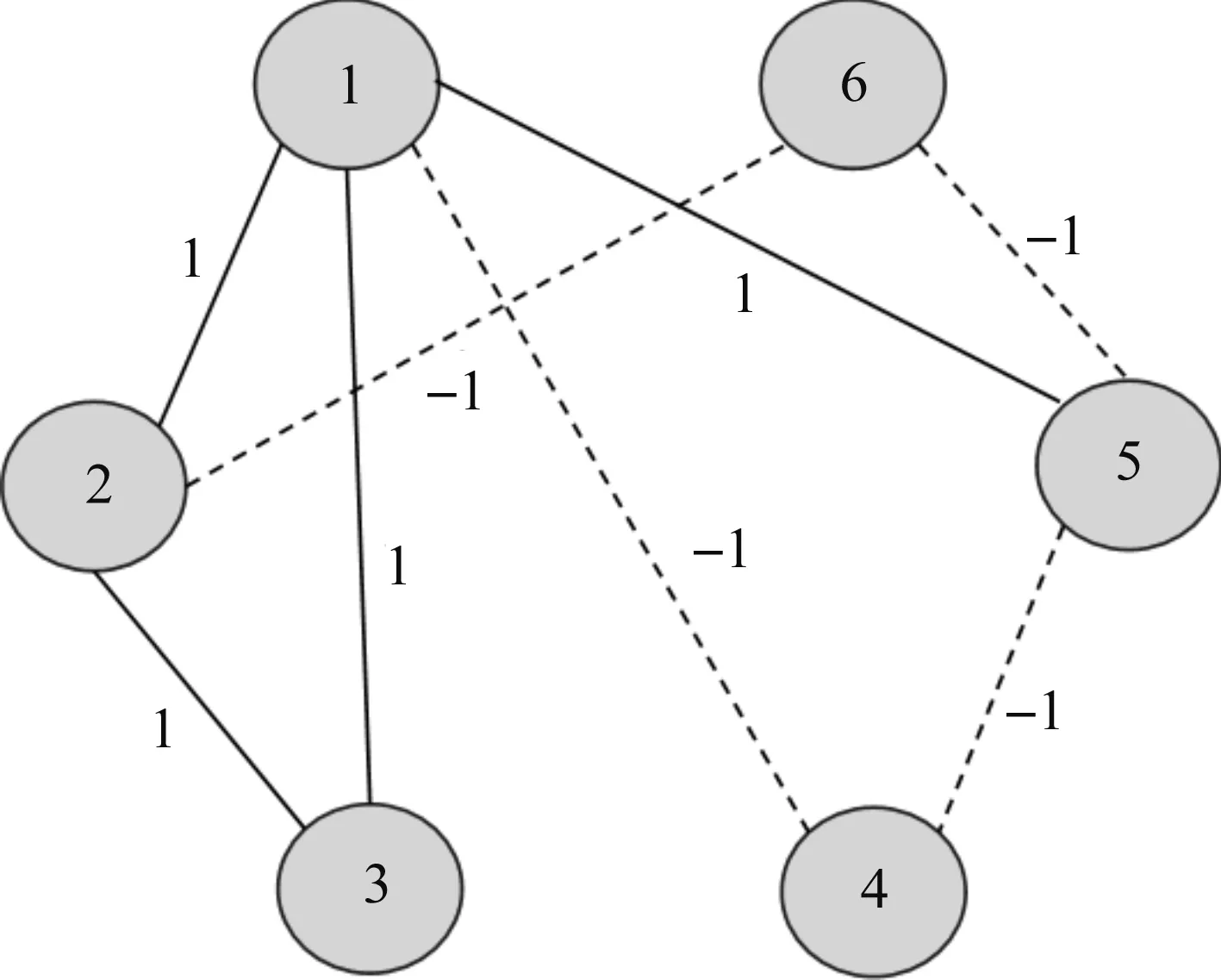
图1 网络拓扑结构
网络拓扑结构多智能体系统的状态方程如下:
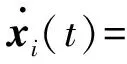

5.2 仿真结果与分析
个体xi的初值选取为:x1=(x11x12)T=(1.315 0 1.208 7)T,x2=(x21x22)T=(0.278 7 -0.110 2)T,x3=(x31x32)T=(1.286 3 -1.691 4)T,x4=(x41x42)T=(1.434 0 1.346 4)T,x5=(x51x52)T=(0.569 9 -1.150 0)T,x6=(x61x62)T=(0.955 4 -0.960 7)T。在非连续静态分布式控制器作用下,随着时间t的演化,个体状态xi=(xi1xi2)T的轨线如图2所示。
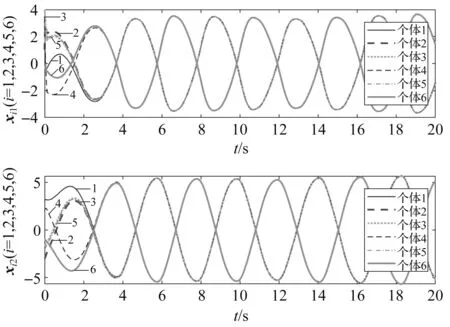
图2 多智能体系统中个体状态轨迹图
从图2可以看出,合作智能体最终达成同向一致,竞争智能体与合作智能体最终达成反向一致,6个异质个体实现了二分。
随着时间t的演化,个体误差ei=(ei1ei2)T的轨线如图3所示。从图3可以看出,当多智能体实现二分集结时,各智能体之间的距离为0。所以,在满足定理的充分条件下,多智能体系统最终渐进实现鲁棒二分一致性,验证了本文设计的非连续静态分布式控制器的有效性。
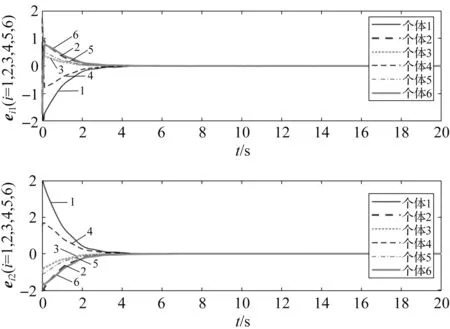
图3 误差轨迹图
6 结束语
针对带有匹配不确定项和非线性时滞项的多智能体系统,本文设计了一类非连续静态分布式控制器,克服了由时滞和扰动带来的不利影响,使得多智能体系统渐进实现了鲁棒二分一致性。后期将针对具有领导者的合作竞争网络的二分跟踪一致性展开进一步研究。
