定频干扰下的基于时频谱熵的跳频信号检测

李 春，赵知劲，2，岳克强，叶学义

(1.杭州电子科技大学通信工程学院，浙江 杭州 310018；2.中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室，浙江 嘉兴 314001)

0 引 言

跳频通信具有截获率低、组网方便、抗干扰能力强等特点，是军事通信的主导技术之一。近年来，跳频信号检测成为通信对抗和监测的热点。跳频信号检测方法分为非盲检测和盲检测。文献[1]提出一种基于压缩接收机的检测方法，但对宽带跳频信号的检测能力不够。文献[2]采用最大似然接收器进行跳频信号的检测，随着候选频率跳数的增多，检测性能下降。文献[3]使用辐射计在各个信道进行测量，根据信道检测结果判断是否存在跳频信号，但检测性能较差。文献[4]在信道化接收算法的基础上，对判决门限进行改进，利用重叠滑动窗估计检测门限，降低了虚警概率，但算法复杂度较高。文献[5]在传统的信道化处理的跳频信号检测算法基础上，设计了一种基于分层处理的跳频信号检测模型，降低了计算量，但检测性能低。文献[6]运用信号化接收的各通道自相关函数进行跳频信号的检测，但算法复杂度较高。文献[7]对信号进行信道化处理之前，通过主成分分析(Principal Component Analysis，PCA)抑制噪声和突发信号的干扰，再对各信道进行短时能量对消，消除定频信号的干扰，实现了跳频信号的检测，但计算量偏大。文献[8]提出一种基于时频矩阵自适应阈值的检测算法，但低信噪比下的检测性能较差。以上检测方法都需要已知跳频信号跳速等参数，属于非盲检测，相比而言，无需已知先验信息的盲检测更加实用。文献[9]提出一种基于功率谱对消的检测算法；为了减少了计算量，文献[10]将信号直接分为2段来计算功率谱对消比，但低信噪比下的检测性能急剧降低。跳频信号具有非平稳特性，时频分析能够反映信号在时间-频率平面上的分布情况，目前常用短时傅里叶变换进行时频分析，时频谱包含跳频信号的丰富特性，常作为跳频信号检测的依据。文献[11]利用灰度时频图的边缘特性检测跳频信号；文献[12]利用跳频信号时频稀疏性检测跳频信号；文献[13]运用多天线接收信号的互相关函数检测跳频信号；文献[14]利用支持向量机和信号时频瀑布图的方向梯度直方图特征进行信号的检测；文献[15]利用单源点检测的方法实现跳频信号的检测。但是，这些算法的复杂度较高，且低信噪比下的检测性能不佳。信息熵能综合反映信号随机波动信息，应用成熟广泛。本文引入时频谱熵，利用跳频信号、定频信号和噪声的时频谱随机波动特点，根据时频谱熵的差异，提出一种定频干扰下的基于时频谱熵的跳频信号检测算法，在高斯白噪声背景中，实现了定频干扰下的跳频信号检测，提高了低信噪比下跳频信号的检测性能。

1 短时傅里叶变换与时频谱熵算法

1.1 短时傅里叶变换的时频谱

令接收机截获的观测信号x(t)中仅存在噪声的假设为H0，存在跳频信号、定频信号和噪声的假设为H1，x(t)的二元假设检验模型为：

(1)

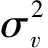
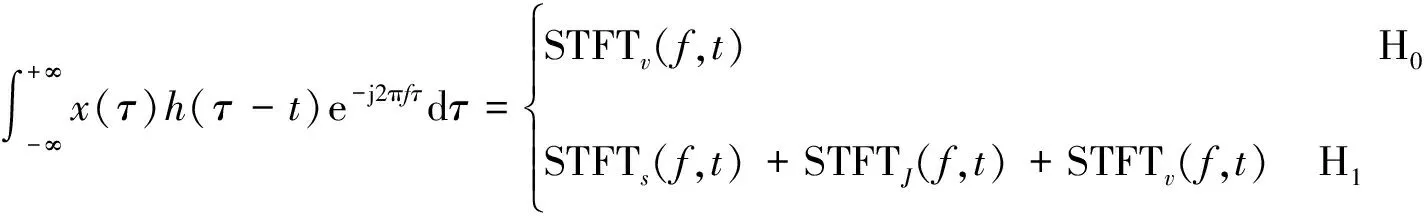
(2)

式中，h(t)为窗函数，STFTs(f,t)，STFTJ(f,t)和STFTv(f,t)分别表示为s(t)，J(t)和v(t)的短时傅里叶变换，j为虚数单位。

对接收信号x(t)进行采样，窗长为L，每次滑动一定长度，得到其短时离散傅里叶变换STFTx(m,n)，信号的时频矩阵为：

(3)

式中，频率维度m=1,2,…,M,M=L/2，时间维度n=1,2,…,N。

H0和H1假设下的接收信号时频谱示例如图1所示。

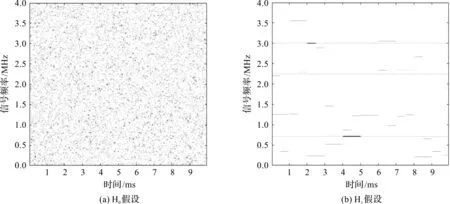
图1 不同假设下，接收信号时频谱

从图1可以看出，噪声的时频谱随机均匀分布；跳频信号的时频谱在局部时频范围内有值；定频干扰信号的时频谱为一条直线，并且某个频率上的时频谱不为0，其他为0。

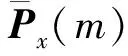
(4)

(5)

式中，频率维度m=1,2,…,M,M=L/2，时间维度n=1,2,…,N。得到图1(b)的归一化时频对消谱如图2所示。

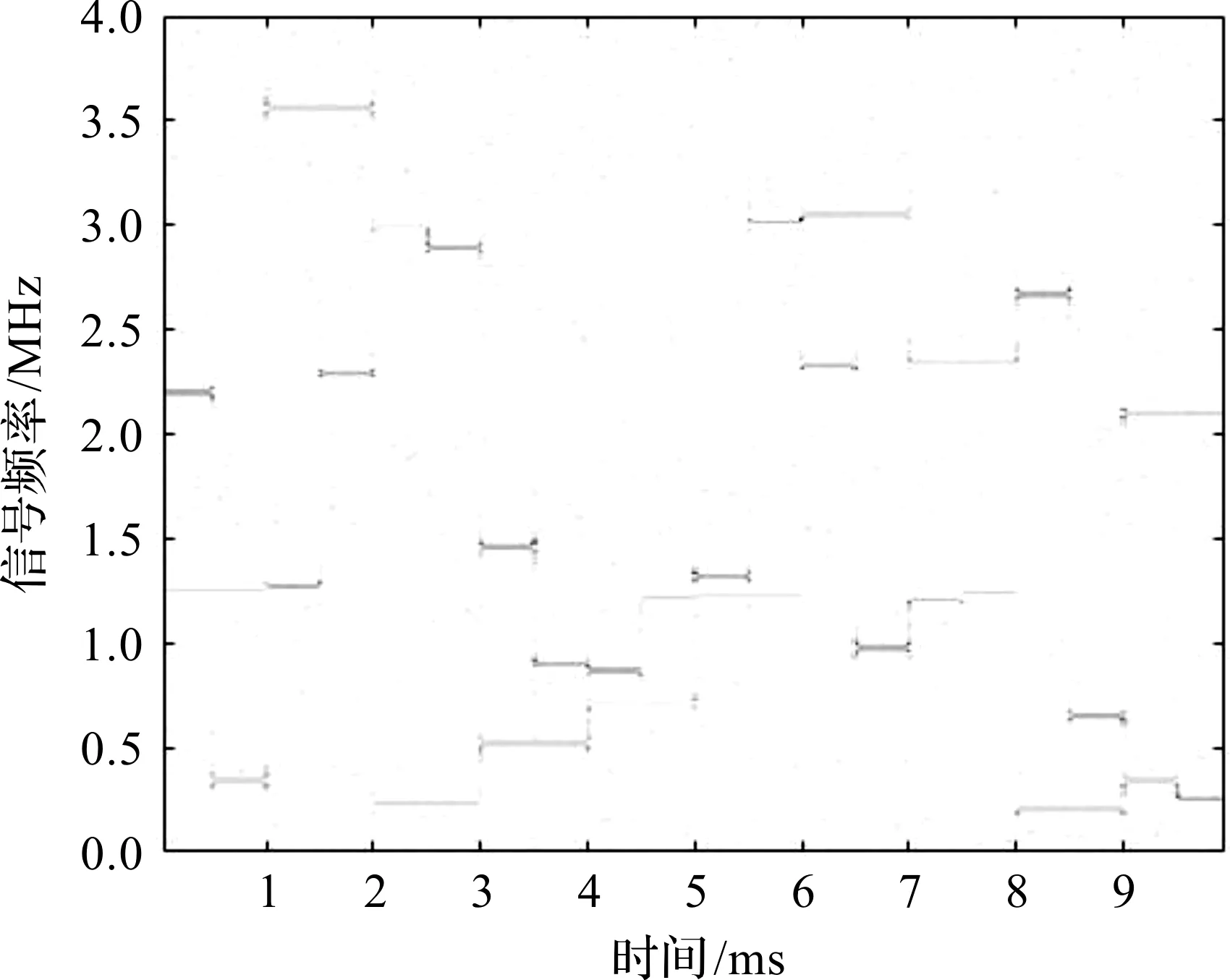
图2 信号时频对消谱

从图2可以看出，采用时频对消方法后，时频对消谱中仅存跳频信号和噪声，较好地消除了定频信号分量。

1.2 时频谱熵算法及原理

因跳频信号、定频干扰信号和噪声的时频谱波动的不确定性不同，通常用信息熵来表示这种不确定性，所以，本文将随机性的信息熵作为统计检验量。假设观测信号x(t)中每个样本出现的概率为：

Px={px1,px2,…,pxi,…，pxK}

(6)

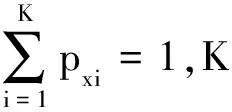
(7)

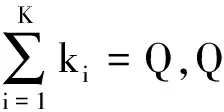
(8)

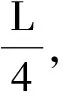
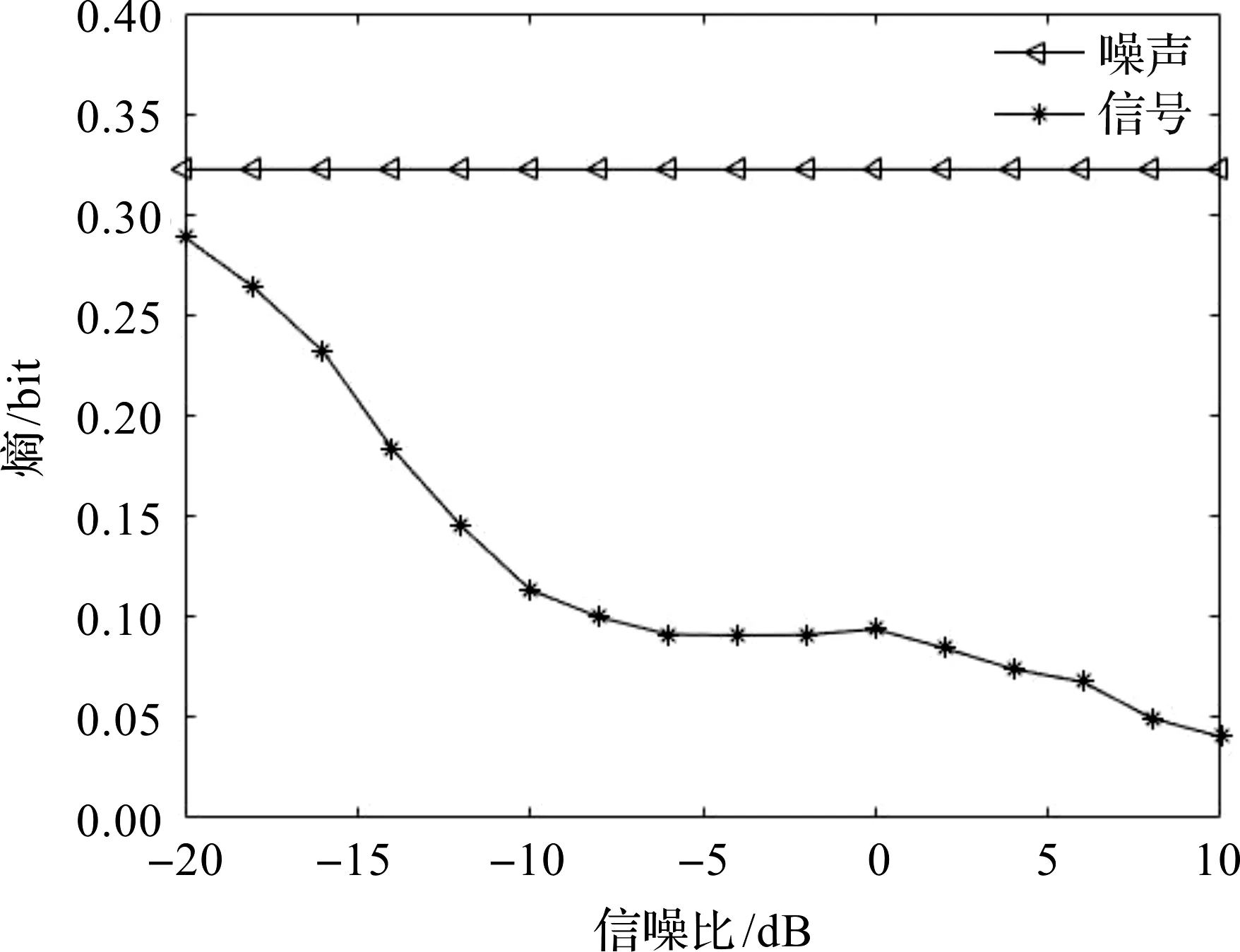
图3 不同信噪比下，信号和噪声的时频谱熵

从图3可以看出，噪声时频谱熵值较大，且不随噪声方差变化；存在跳频时，时频谱熵值较小。从而得到跳频信号判决规则如下：

(9)

式中，λ为判决门限。

2 仿真实验与分析

信号采样频率为10 MHz，采样长度为100 000点。2个跳频图案分别为[1.25,3.56,0.23,0.52,0.71,1.23,3.05,2.34,0.21,2.10] MHz和[2.20,0.34,1.27,2.29,3.00,2.89,1.46,0.90,0.87,1.22,1.32,3.01,2.33,0.98,1.21,1.24,2.67,0.65,0.34,0.25] MHz，跳周期分别为1.0 ms和0.5 ms，定频信号的频率分别为0.71 MHz，3.00 MHz和2.25 MHz。其中每一条曲线是10 000次实验结果的平均值。

2.1 窗长对检测性能的影响

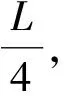
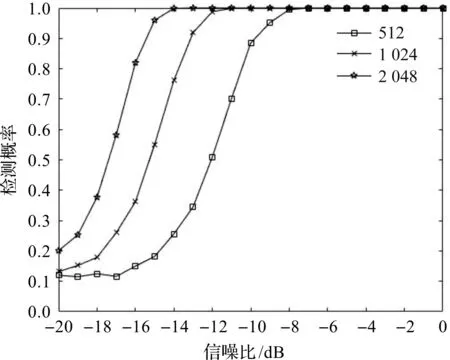
图4 不同窗长下的跳频信号检测概率

从图4可以看出，随着窗长的增加，跳频信号检测概率提高。窗长越长，包含的跳频信号信息越全，检测概率越高，但算法复杂度增大，实时性也变差。因此，本文折中考虑，选取窗长为1 024。

2.2 滑动步长对检测性能的影响

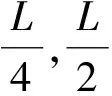
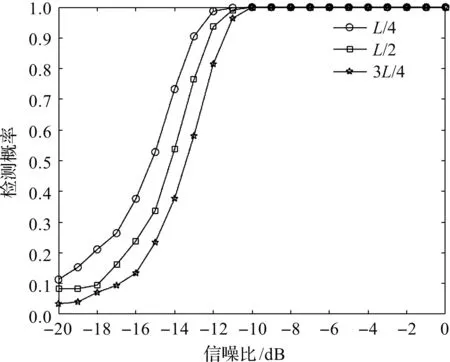
图5 不同滑动步长下的跳频信号检测概率

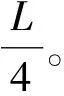
2.3 抗噪声功率不确定性分析

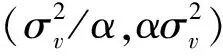
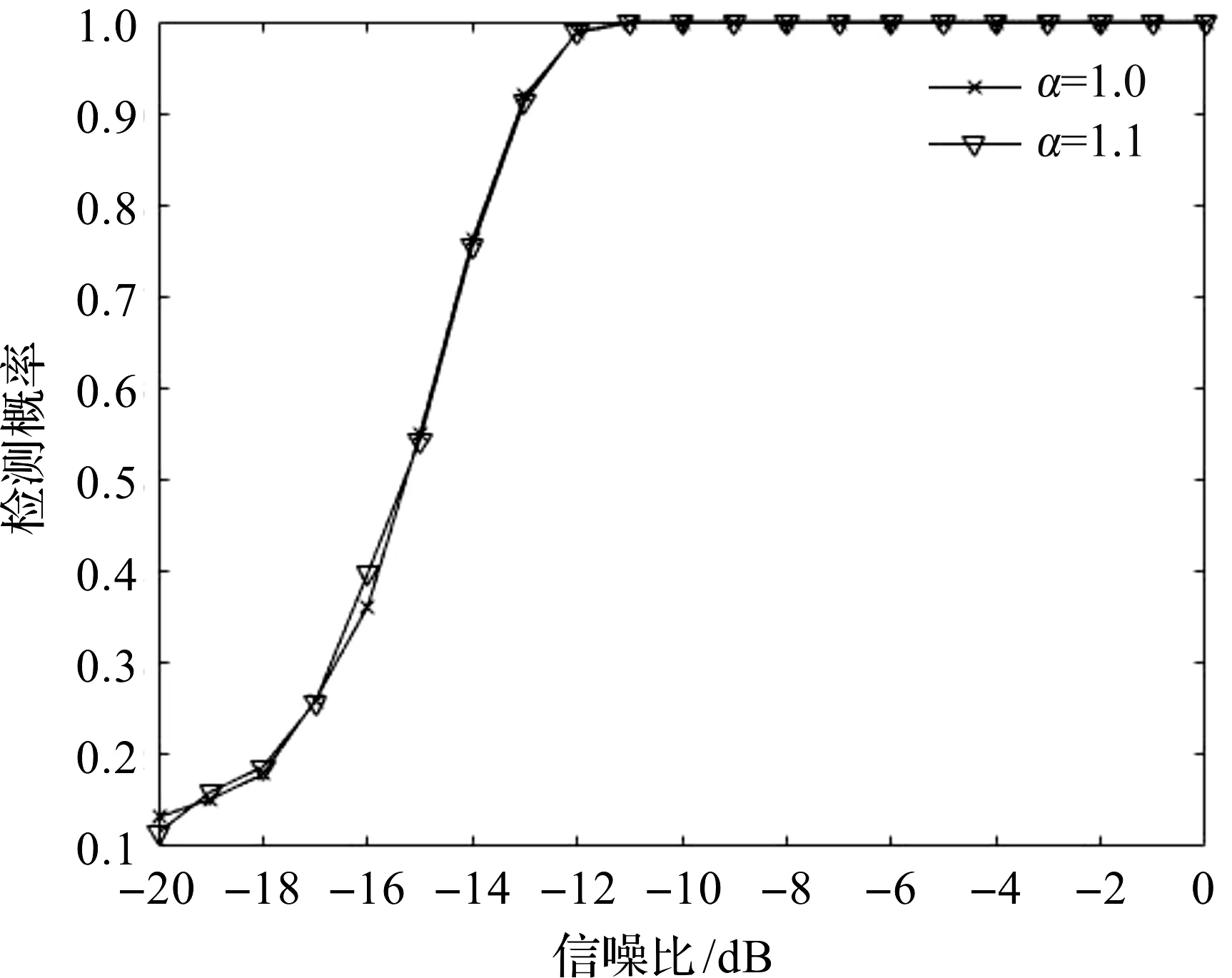
图6 抗噪声功率不确定性分析

从图6可以看出，本文提出的定频干扰下的基于时频谱熵的跳频信号检测算法基本不会受噪声功率不确定性的影响。

2.4 算法检测概率对比

噪声功率不确定度取α=1.0，其他实验参数同2.3节。在高斯白噪声背景下，存在定频干扰时，分别采用本文算法和文献[9]的功率谱对消算法进行跳频信号检测，得到跳频信号检测概率如图7所示。

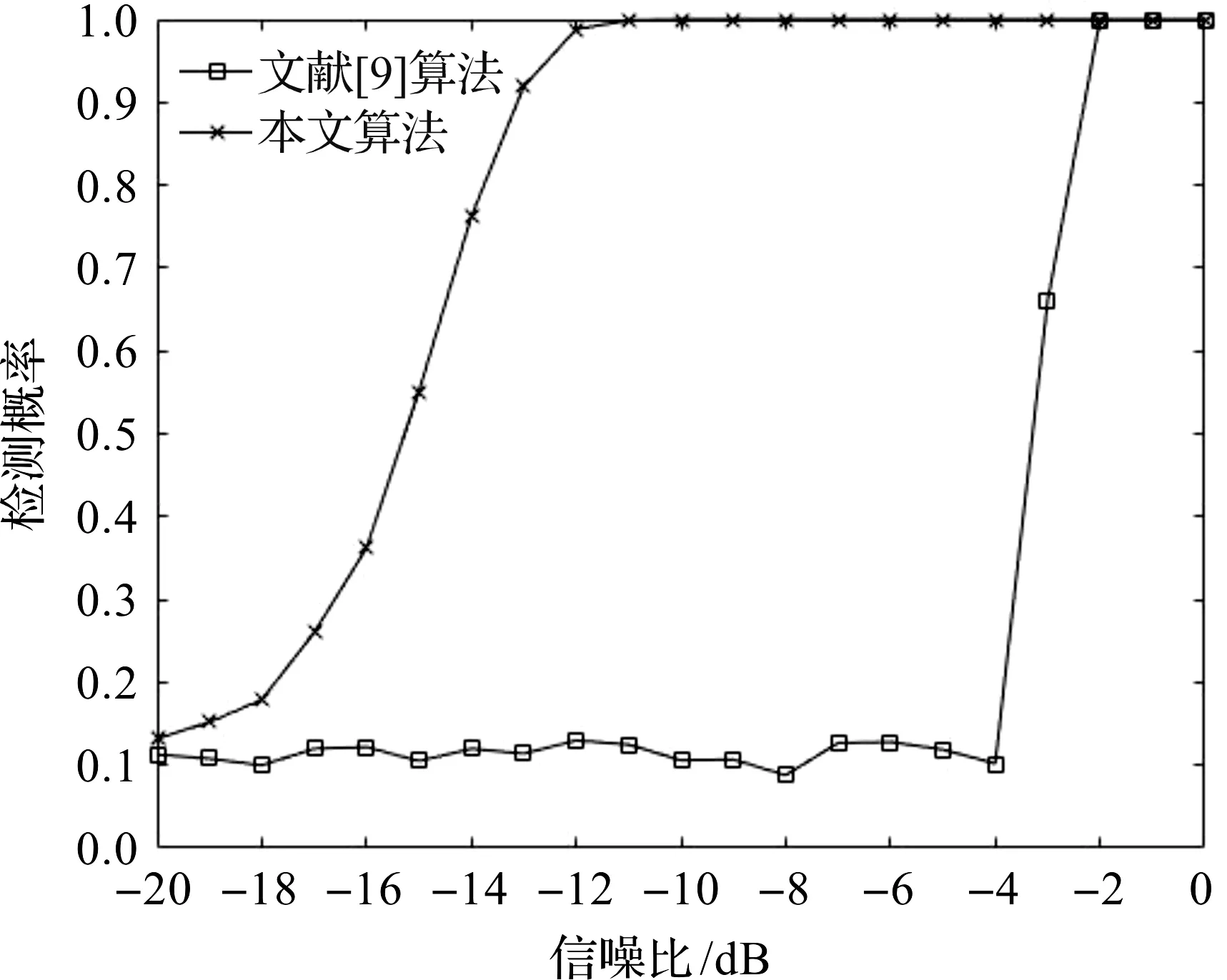
图7 不同算法的检测概率

从图7可以看出，当信噪比大于-12 dB时，本文算法对跳频信号的检测概率可达100%，优于文献[9]的功率谱对消算法。

3 结束语

本文利用跳频信号、定频信号、高斯白噪声的时频谱具有的不同局部特征，构造了时频谱熵并作为检测统计量，实现了高斯白噪声和定频信号干扰背景下的跳频信号检测，具有抗噪声功率不确定性。在低信噪比下，检测性能优于功率谱对消对比算法。但是，本文只考虑存在定频干扰信号的跳频信号检测，后续将针对复杂环境下的跳频信号检测展开深入研究。