基于模糊RBF神经网络的无刷直流电机PID控制
2022-08-23顾文斌杨生胜王贤良苑明海
顾文斌,杨生胜,王贤良,苑明海
(1.河海大学 机电工程学院,江苏 常州 213022;2.南通河海大学 海洋与近海工程研究院,江苏 南通 226004)
0 引 言
随着电力电子技术、传感器技术以及新型永磁材料等技术的蓬勃发展[1],无刷直流电机(BLDCM)凭借结构简单、动态响应迅速、输出转矩大、可控性好、可靠性高等特点,同时具备良好的启动、调速、制动性能,广泛应用于航天航空以及机器人等领域[2-3]。传统PID控制算法由于结构简单、易于运用到工程实践中,成为电机控制领域最常用的控制算法之一[4]。然而,传统PID控制算法主要基于线性模型,对参数依赖性强,同时抗干扰能力差,并不能满足控制系统的高精度要求[5]。无刷直流电机是一个复杂的非线性时变系统,具有多个变量,而且有很强的耦合性,很难推导出精确的数学模型,所以采用传统PID的控制方式很难达到理想的效果[6]。
近年来,许多专家学者开始研究如何将智能算法与传统PID控制相结合。文献[7]将模糊PID控制运用到直流调速系统中,该方法能使调节时间更短,转速更加平稳;文献[8]针对开关磁阻电机存在严重的转矩脉冲,提出了基于RBF神经网络的瞬时转矩控制策略,该策略控制精度高,响应速度快,能有效减小转矩脉冲;文献[9]将模糊RBF神经网络PID控制运用到电机操动机构中,研究结果表明,该策略能精确追踪断路器动触头的运动。
模糊控制不用依赖数学模型,通过模仿高级动物的思维方式进行决策,克服了传统PID的缺陷,对于复杂的非线性系统,具有良好的控制效果。但模糊控制器对专家的经验知识依赖性强,同时缺乏自学习的能力,利用神经网络自学习、自适应的能力,就能够很好地弥补这一短板[10]。该文将模糊控制与径向基函数神经网络相结合,提出了一种基于模糊RBF神经网络的PID控制策略,并将改进蚁群算法和LM算法引入模糊神经网络训练中,以提高无刷直流电机的控制性能,最后在Simulink中通过仿真验证该策略的控制效果。
1 BLDCM数学模型
无刷直流电机主要由三相定子绕组、永磁体转子、霍尔传感器及逆变器等组成,其中定子绕组为Y接集中整距绕组,转子采用隐极内转子结构,3个霍尔元件在空间相隔120°对称放置[11],其控制系统电路见图1。

图1 无刷直流电机控制系统电路
由于无刷直流电机的梯形波感应电动势,所以无法使用传统的d-q变换对其运动特性进行精确分析。最有效的方法就是相变量法,即以相电流、相电压为状态变量进行分析[12]。
其电压平衡方程如下:
(1)
式中,Ui为三相绕组相电压;R为三相绕组相电阻;ii为三相相电流;Li为三相绕组自感;Lij为三相绕组间的互感;ei为反电动势。
由于无刷直流电机绕组间特殊的连接方式,所以各绕组的自感和互感都相等,于是Li=L,Lij=M,所以有:
(2)
因为,
iA+iB+iC=0
(3)
所以,
MiA+MiB+MiC=0
(4)
于是无刷直流电机的电压平衡方程可替换为:
(5)
无刷直流电机的电磁转矩方程为:
(6)
无刷直流电机的机械特性方程为:
(7)
式(6)中,Te为电磁转矩;ω为机械角速度。式(7)中,Tl为负载转矩;B为阻尼系数;J为转动惯量。
2 改进型PID控制器
2.1 模糊神经网络PID控制器结构
在多变量、非线性及强耦合的复杂时变系统中,传统PID由于参数固定,难以满足控制性能的需求。于是,该文采用一种基于模糊神经网络的PID控制器,实现对Kp、Ki、Kd的实时调整。
在模糊RBF神经网络中,选择合适的参数初始值对训练过程极为重要,它决定了神经网络收敛速度的快慢,而一般情况下,RBF神经网络的参数初始值都是通过K-means等传统聚类方式确定,但K-means等聚类方法很容易陷入局部最优的情况。因此,该文采用改进蚁群聚类的方式来初始化RBF神经网络参数[13]。
针对高斯牛顿法的在步长太大时局部近似不准确的缺陷,LM算法通过给步长添加信赖域,使得在信赖域内可以认为近似等效。它是介于梯度下降法和高斯牛顿法之间的一种非线性寻优算法,非常适用于非线性问题的求解[14]。该文采用LM算法来确定神经网络的权值,提高神经网络的训练速度。模糊神经网络PID控制原理如图2所示。

图2 模糊神经网络PID控制原理
2.2 模糊神经网络结构
模糊RBF神经网络为两输入三输出的四层结构。其中输入层有两个输入:系统偏差e(t)、偏差变化率ec(t);输出层有三个输出:Kp、Ki、Kd;通过改进蚁群算法来确定模糊化层和模糊推理层的神经元个数及神经元中心;利用LM算法确定基宽、权值。图3为模糊神经网络结构。
(1)输入层。该层含有两个神经元节点,连接两个输入量,通过激活函数f1(xi)=xi输出到模糊化层。
(2)模糊化层。该层将上一层的两个输入量进行模糊化,输入量隶属度函数的论域为[-6,6],模糊子集为{NB,NM,NS,ZO,PS,PM,PB},以高斯函数作为各节点的激活函数。
(8)
式中,cij为隶属度函数的中心,σij为隶属度函数的基宽。
(3)模糊推理层。该层的节点与每条模糊规则一一对应,模糊控制规则如表1所示。该层的作用是将上一层模糊化后的输入量,根据模糊规则进行模糊推理,得到输出值。
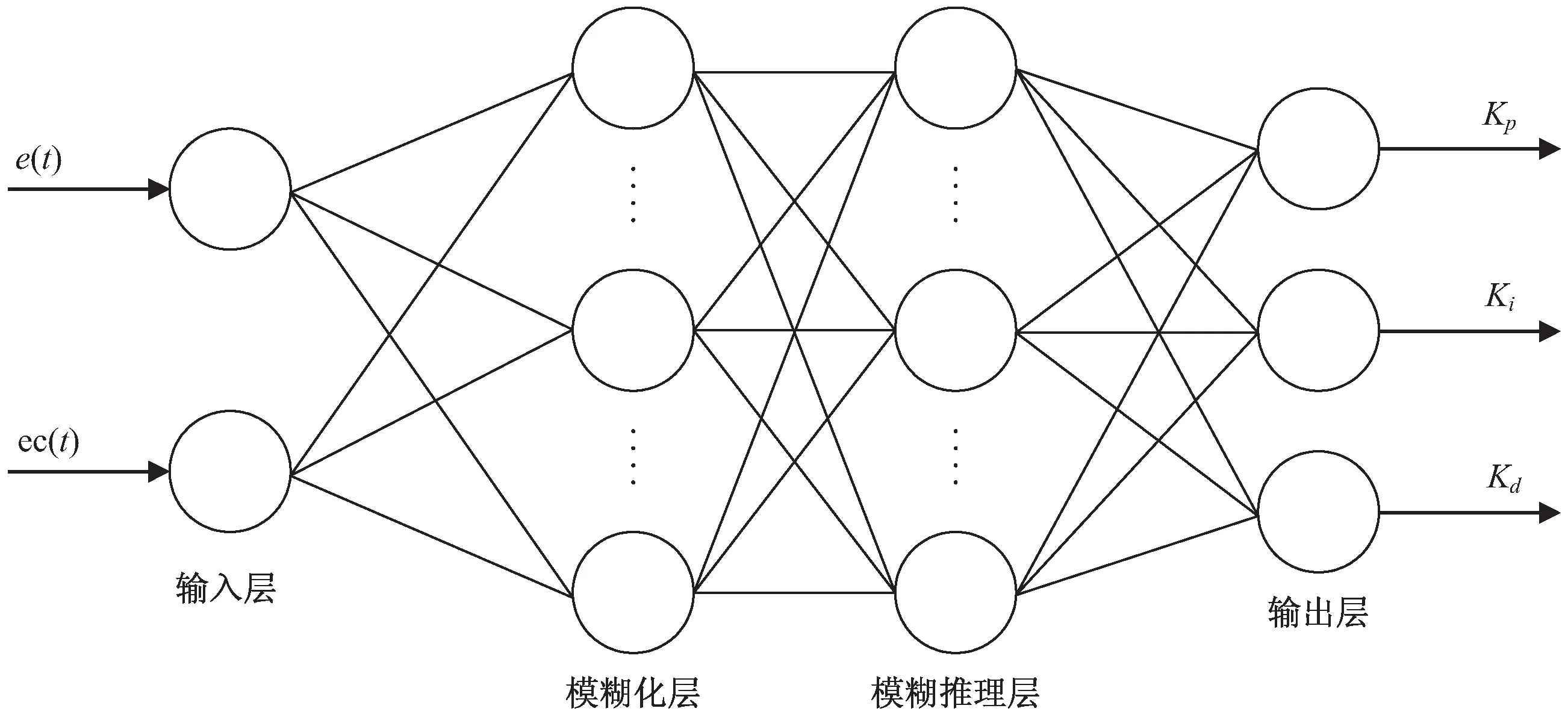
图3 模糊神经网络结构

表1 模糊控制规则表
各节点的激活函数为:
(9)
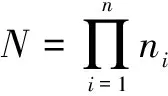
(4)输出层。该层是将上一层中的输出量清晰化,输出Kp、Ki、Kd,其激活函数为:
(10)
即:
(11)
式中,ω是模糊推理层与输出层之间的连接权矩阵。
2.3 模糊神经网络的参数初始化
K-means等传统聚类方法在处理数据时,存在缺陷,达不到令人满意的效果。该文在数据处理时采用改进蚁群算法进行聚类[15-16],通过自适应的方法改变持久性系数,提高收敛速度。其过程如下:
(1)初始化样本个数N,聚类半径r,样本属性m,允许误差ε0,概率p0等参数。
(2)确定两样本之间的距离:
dij=‖xi-xj‖2i,j=1,2,…,N
(12)
如果dij小于r,信息素为1,否则为0。
(3)计算xi到xj的概率:
(13)
更新方程:
(14)
如果Pij大于p0,则xi和xj归一类;否则为不同类。上述公式中,τij为信息素;ρ为持久性系数,一般取值范围[0.5,0.9];Q为一正常数。
(4)计算与xi同类的中心点:
(15)
求出总体误差:
(16)
如果ε小于ε0,则停止; 否则继续分类计算。
(5)计算信息素的持久性系数。
因为ρ减小不会影响收敛速度,所以当求得的最优值在多次循环后,仍未发生显著改变,可以根据下列公式减小ρ的值,其中ρmin为ρ的最小值。
(17)
重复上述步骤,当精度达到要求时可求得所需的K个聚类中心。
(6)确定系统的基宽:
(18)
式中,I为隐层单元个数,dmax为所选中心之间的最大距离。
2.4 模糊神经网络的训练算法
LM算法既有高斯牛顿算法局部收敛的优点,全局搜索速度又比梯度下降法快,成为目前神经网络最常用的训练算法[17]。该文将LM算法运用到模糊神经网络的训练中,以确定基宽和权值[18-19]。
(19)
式中,u>0,I为单位矩阵,en'为误差分量。
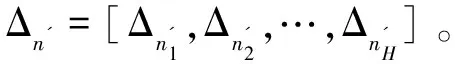
Δn'+1=Δn'+Δx
(20)
以误差指标函数为成本函数,即:
(21)
式中,P为样本数量,N'为节点数量,第i个样本的第k个误差ei,k=di,k-yi,k,其中di,k为期望输出,yi,k为实际输出。
假设允许误差δ,最大迭代次数Kmax,以组合系数μ=0.01,调整参数α=10作为算法起点,输入参数向量Δ1的神经元基宽取蚁群聚类后的值,En'为第n'次迭代时的成本函数。
步骤一:从初始值n'=1开始,计算成本函数E1。
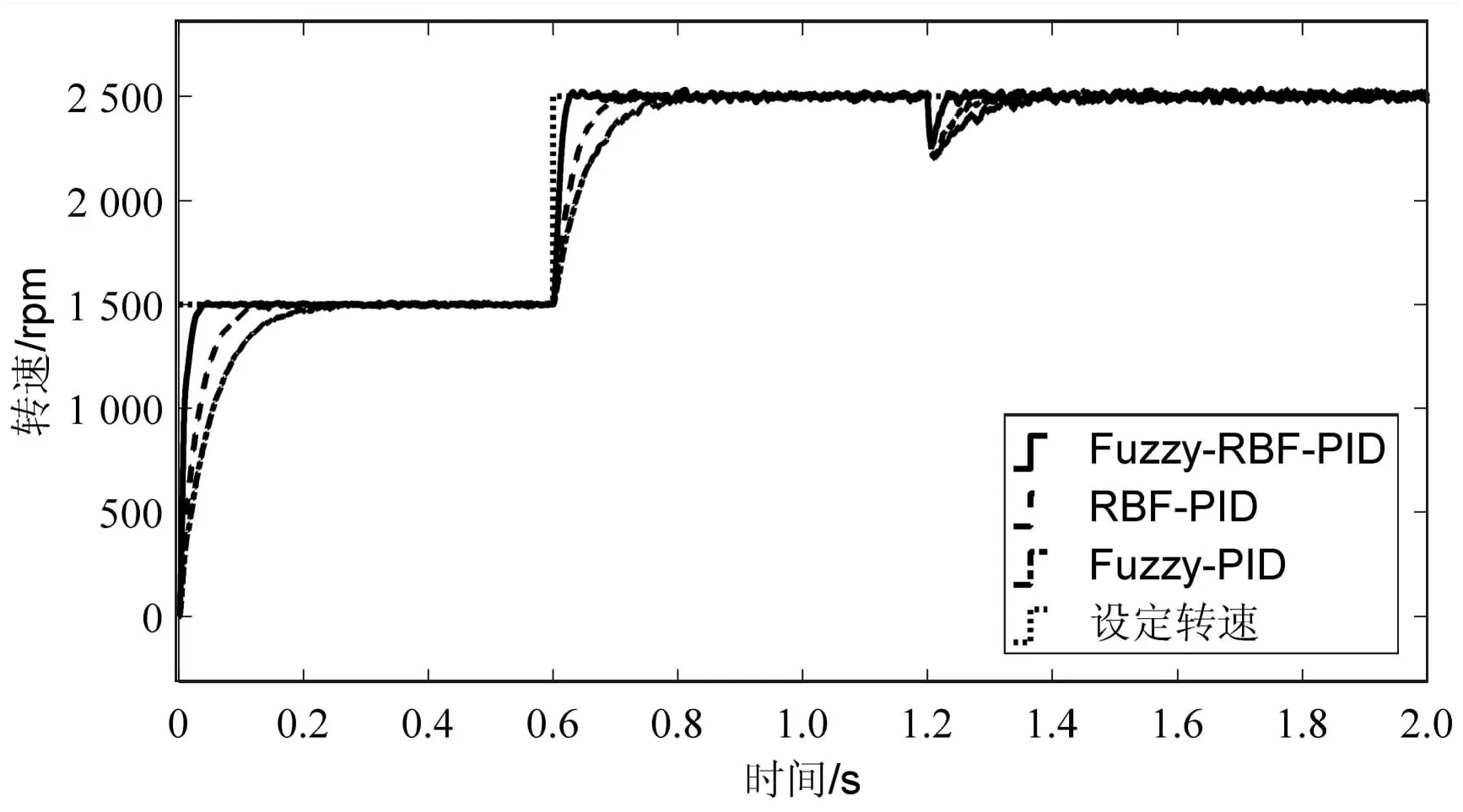
步骤二:若En'>δ,n' (1)计算雅可比矩阵Jy。 (22) (3)调整参数。 (23) (4)令n'=n'+1,计算新的成本函数En'。 (6)返回步骤二。 步骤三:根据输出参数向量Δn'+1,得到神经元的基宽以及权值。 无刷直流电机控制模型主要由电机本体、速度反馈模块以及电流反馈模块等部分组成。在双闭环控制系统中,电流内环采用PI控制;鉴于传统PID不能根据实际工况及时调整参数,而速度外环又是控制系统的关键环节,因此该文速度外环采用模糊神经网络控制,以提高控制系统的响应速度、抗干扰能力[20]。图4为无刷直流电机双闭环控制系统框图。 图4 无刷直流电机控制系统框图 在Simulink中建立基于模糊径向基函数神经网络的无刷直流电机仿真模型,并与其他PID控制下的仿真模型进行对比,验证该文所提出的控制策略的优越性[21]。首先,以阶跃信号为输入信号,仿真时间为2 s,无刷直流电机初始速度设定为1 500 r/min,在0.6 s时转速上升到2 500 r/min,然后在1.2 s时受到5 N·m的干扰,经过Simulink仿真得到如图5所示的无刷直流电机的转速曲线。 图5 无刷直流电机转速曲线 由图5分析可知,初始转速为1 500 r/min时,模糊RBF控制在0.15 s内达到稳定状态,而RBF神经网络控制在0.25 s后达到稳定状态,模糊控制在0.3 s后达到稳定状态;当转速上升到2 500 r/min时,模糊RBF控制能更快地响应速度的变化并达到稳定状态;在受到5 N·m的干扰时,模糊RBF控制下转速的波动相对较小,而且能以更短的时间回复到稳定状态。 该文针对无刷直流电机在传统PID控制下存在抗干扰能力差、响应速度慢以及控制精度低等问题,设计了一种基于模糊RBF神经网络的无刷直流电机PID控制策略。利用模糊控制降低传统PID控制器对数学模型的依赖性,将神经网络与模糊控制结合,增强系统的自学习、自适应能力,在初始化神经网络的参数时引入改进蚁群聚类算法,通过LM算法提高神经网络的训练速度。最后,在Simulink中与其他控制策略进行对比。仿真结果表明,设计的模糊RBF神经网络PID控制策略比其他控制策略具有更优异的控制性能,能极大提高无刷直流电机的响应速度、控制精度以及抗干扰能力。在未来的研究中,可以将此控制策略改进,与其他优秀的算法结合,进一步提高控制性能。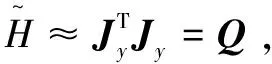
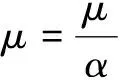
3 仿真搭建与结果分析

4 结束语
