指向核心素养的小学数学“统计图”习题研究

魏加加

(石河子大学 师范学院，新疆 石河子 832000)

随着课程改革的深入，提高学生核心素养、关注学生全面且个性化发展成为基础教育的新诉求。《义务教育数学课程标准(2011年版)》提出，通过义务教育阶段的数学学习，学生能够“获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”。因此，从核心素养培养的视角对现行教科书中的习题进行研究非常必要[1]。

统计是一种数学思想，也是认识客观事物、描述生活现象、解决问题的一种方法。学习统计可以了解并掌握基本的统计知识和方法，从统计的角度分析实际问题，强化问题意识，提高统计能力。以人民教育出版社、北京师范大学出版社、江苏教育出版社发行的小学《数学》教科书(以下分别简称人教版、北师大版、苏教版)中“统计图”教学主题的课后习题为研究对象，基于鲍建生2014年修订的习题综合难度模型，分析习题难度，并从核心素养角度分析习题设置。

1 教科书习题难度研究

3种版本教科书关于“统计图”教学主题的课后习题基本内容如表1所示。基于鲍建生2014年修订的习题综合难度模型，从背景水平、数学认知水平、运算水平、推理水平、知识含量水平对习题难度进行具体分析。

1.1 背景水平

小学知识点单一，呈现形式灵活。“统计图”教学主题的内容与生活息息相关。如图1所示，3种版本中“无背景”的习题较少，“个人生活”比例较高。数学应用生活化可强化学生的主体意识。“公共常识”方面，苏教版较低，为20.51%。“科学情境”方面有待提高。

1.2 数学认知水平

数学学习过程是数学认知过程。如图2所示，“概念”比例最高，这反映课后习题注重数学基础知识；“操作”与“分析-探究”比例不高。课后习题需学生独立完成，故应提供充足的时间，让学生体验学习的乐趣，培养分析能力。“分析-探究”水平的习题类型应提高开放性、推理性、生活性。“领会-说明”比例最低，不利于学生核心素养的提高，理解能力和表达能力的提高。

1.3 运算水平

运算能力是根据运算法则、运算律等正确运算的能力。关于运算水平的统计结果详见图3。教学主题是统计图，注重解读统计图，所以“无运算”“数值运算”水平比例很高，符合“熟能生巧”的教育理念。关于“简单符号运算”的习题只有1道，而且是直接运算关于x的方程。关于“复杂符号运算”的习题为0。应合理分配习题比例，提高核心素养。

图3 运算水平(版本比较)

1.4 推理水平

数学推理是由已知条件推断结论的思维形式。关于推理水平的统计结果详见图4。“复杂推理”水平比例最低，只有人教版高年级学段有1道题(这道题是整理并表示数据，你发现了什么？笔者认为，可以分3步：整理所搜集的数据；绘制合适的统计图，并标上数据；从统计图中你发现了什么？)。有研究表明，儿童缺少知识和经验，但不缺乏推理能力，其推理能力伴随自身成熟逐步提高，并需依托数学学习积累经验。

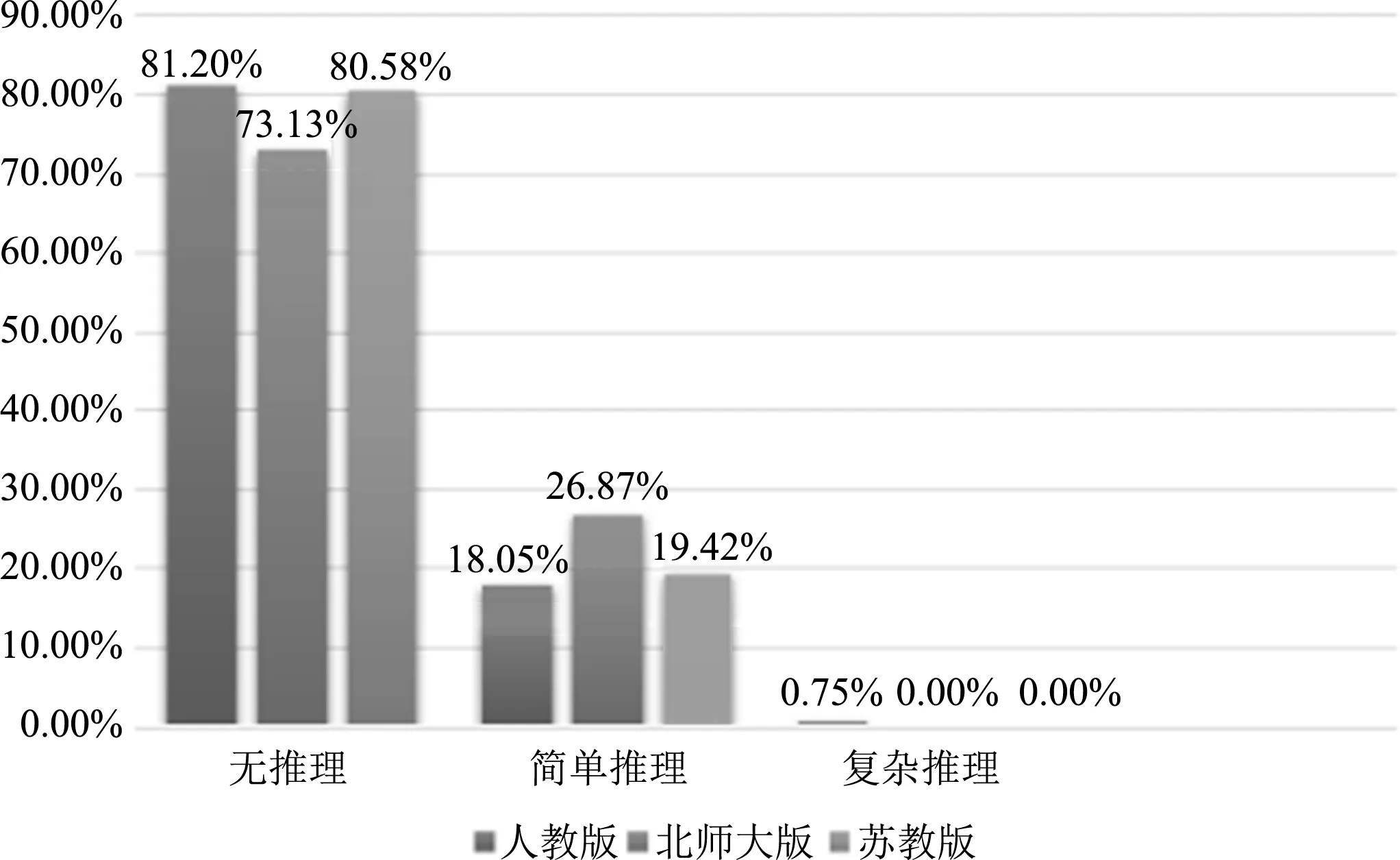
图4 推理水平(版本比较)

1.5 知识含量水平

关于知识含量水平的统计结果详见图5。含“单个知识点”的习题数量差异较大，含“2个知识点”“3个以上知识点”的习题，人教版比例最高。整体上看，人教版和北师大版的知识点含量分布比较合理，苏教版过多注意单个知识点。

图5 知识含量(版本比较)

1.6 习题综合难度分析

图6所示的是习题综合难度因素水平加权平均的统计数据。习题综合难度的五边形模型整体上不够完备。小学数学“统计图”教学主题的习题在运算水平方面缺失较多，推理水平方面也有欠缺。3种版本中，背景水平方面相差不多，数学认知水平方面，苏教版稍弱，知识含量水平方面，人教版略高。

图6 习题综合难度

2 高、低年级学段习题难度模型分析

3种版本教科书低年级学段(1—3年级)与高年级学段(4—6年级)习题内容见表1。

2.1 背景水平

关于背景水平的统计结果详见图7。“无背景”比例很少，低年级学段课后习题都有背景。高年级学段是3.73%(人教版五年级下册有1道题：小组合作调查一项你们感兴趣的事例，用统计表、统计图呈现)。“个人生活”方面，低年级学段比例很高，随着知识难度的增加，高年级学段有所下降。“公共常识”比例在高年级学段有所上升。“科学情境”比例较低，低年级学段为0，高年级学段为10.56%，而且集中在六年级学段。如人教版六年级下册有关于牛奶含有的营养成分所占比例的题目。适当增加科学情境的习题数量很有必要。

图7 背景水平(学段比较)

2.2 数学认知水平

关于数学认知水平的统计结果详见图8。小学教学注重“双基”，“概念”水平比例较高。考虑学生的理解力，涉及较复杂、抽象的概念题多放在高年级学段。受限于学生认知发展水平，低年级学段的操作习题较多。“领会-说明”“分析-探究”水平比例不高，应有所增加，以拓展学生的思维，培养他们的创新能力。

图8 数学认知水平(学段比较)

2.3 运算水平

如图9所示，直观分析统计图，“无运算”和“数值计算”比例差不多。高年级学段注重数据分析，着重培养数学思维。“符号运算”比例是0。高年级学段应渗入简单的符号运算，以便与初中无缝衔接。

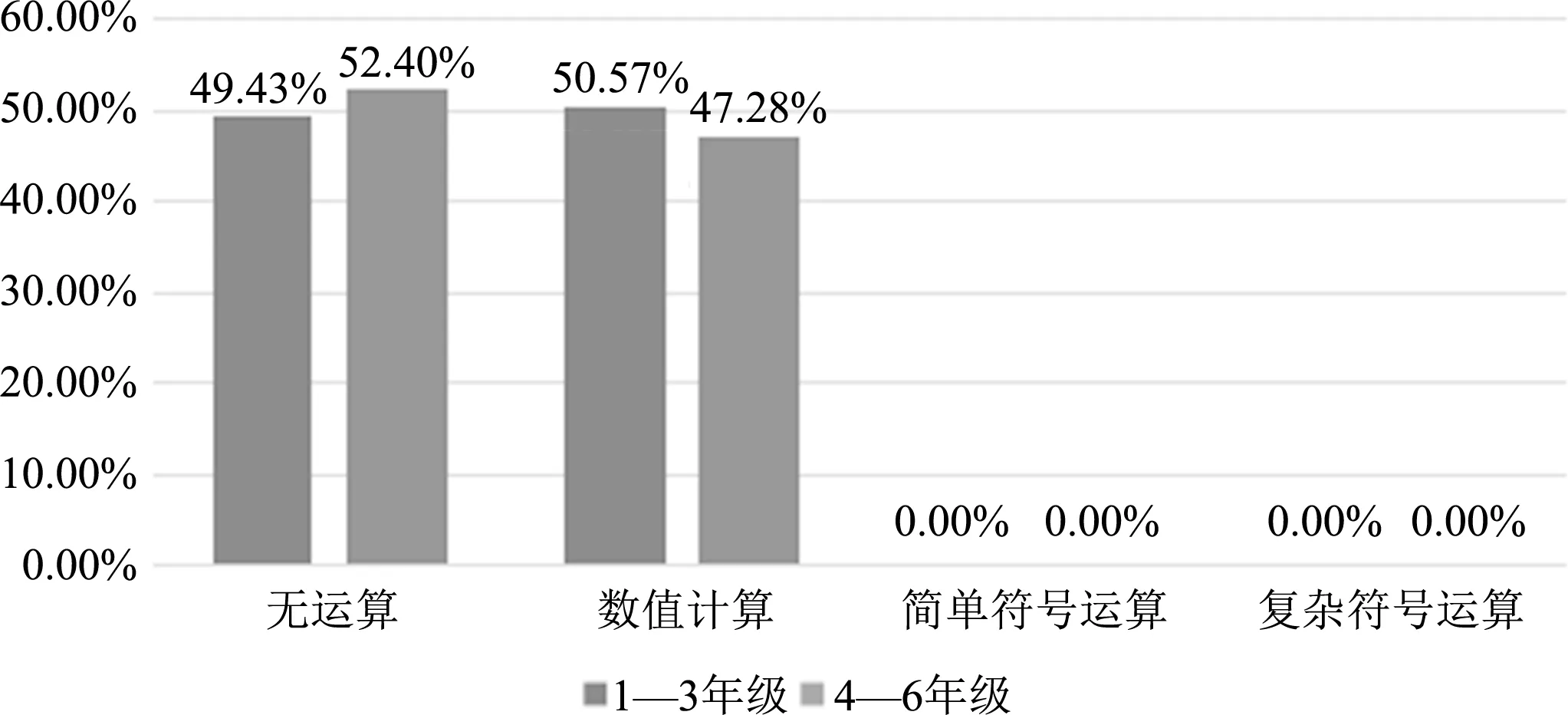
图9 运算水平(学段比较)

2.4 推理水平

如图10所示，“无推理”水平比例最高，随着年级的升高，“简单推理”比例逐渐提高。复杂推理指包含3个及以上推理步骤的推理。高年级学段关于复杂推理的习题仅有1道，可适当增加。

图10 推理水平(学段比较)

2.5 知识含量水平

如图11所示，“单个知识点”比例较高。低年级学生知识水平较低，罗列多个知识点可能导致学生解答困难，随着学生年龄增长、认知发展，可以适当增加关于2个或3个以上知识点的题目，为后续学习打好基础。

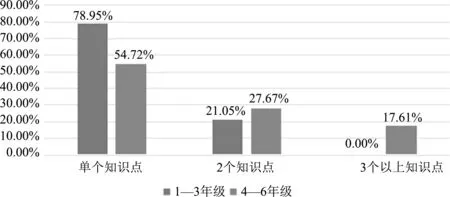
图11 知识水平(学段比较)

3 习题编制及应用建议

3.1 精选课后习题

习题应贴近生活，与实际相联系[2]，题干设计应与时俱进，新颖有趣。很多教师尝试用问题激发学生兴趣[3]。问题设计要精练准确且富有意义。课后习题应以精、广为主，可以增加一些公共常识、科学情境方面的题目，以帮助学生扩充知识，提高阅读能力。融合各学科知识点有利于培养学生跨学科学习能力，提高综合能力[4]。

3.2 增设开放性环节，发展发散性思维、抽象思维

开放性问题具有一问多答的思维特征，并赋予数学问题一定的弹性，可以帮助学生跳出固有思维，选择合适的解题途径。“统计图”主题下的习题大多没有出现简单符号，这不利于学生发散思维、抽象思维的发展。笔者曾以一道题为例，在某四年级班级进行测试，题目如下：

王叔叔每天沿着环形跑道跑步并记录，第1天6 km，第2天5 km，第3天4 km，第4天没有跑。以此类推，如果第4天王叔叔跑步会跑多少 km？王叔叔第n天跑多少 km？测试结果显示，46名学生中，32人能回答如果第4天王叔叔跑步会跑3 km，只有2人回答第n天跑(6-n+1)km。教学中应适当加入简单符号。

3.3 利用大单元教学培养数学思维

“统计图”主题教学分布在各年级，目录相对统一，如北师大版中，数据的整理和表示(三年级下册)、数据的表示和分析(四年级下册、五年级下册)、数据处理(六年级上册)。这些知识点相互关联，可以运用大单元的方式整合，设计大单元教学[5]。知识点的衔接也很关键，具有承前启后、拓展延伸的作用。

3.4 评价标准多元化，关注表现型评价需求

指向核心素养的数学教学注重培养学生的交际能力、合作能力、创新能力、抽象能力等，倾向于多元智力理论，有必要增加表现性评价[6]。应结合学生日常经验和公共常识，设置多种题型，如开放题、动手操作题、现实调查题、创新题等，在习题应答方式上，应增加小组合作汇报、组间交流、成果展示、实践动手操作等。而作为表现性评价任务的习题必须关注信度和效度，确保核心素养培养。