基于全变分与交替保边扩散平滑的稀疏角度CT重建算法

张莹芳，陈 平，潘晋孝

(1.中北大学 信息与通信工程学院，太原 030051；2.中北大学 信息探测与处理山西省重点实验室，太原 030051)

0 引言

X射线计算机断层成像(Computed Tomography，CT)是用X射线对物体进行断层扫描，利用从多个角度获得的投影数据重建物体截面信息的成像技术[1]。该技术以其快速采集和高空间分辨率等优点在临床诊断中得到了广泛的应用[2]。但CT扫描会产生大量的X射线辐射，过多的X射线辐射可能导致癌症和遗传性疾病[3]，为了降低CT扫描导致的患病风险，稀疏角度CT成像技术越来越受到人们的关注[4]。

稀疏角度CT重建是一种通过减少投影角度的数量来降低辐射剂量的方法[5]，但受经典的奈奎斯特采样定理要求的限制，认为从欠采样的数据重建断层图像是不可行的，现在得益于压缩感知(Compressed Sensing, CS)理论的存在，许多不适定的逆问题包括稀疏角度CT问题都可以通过压缩感知技术得到有效地解决[6]。但商业中应用最广泛的滤波反投影(Filtered Back-Projection, FBP)解析重建算法对投影数据的完备性有特定的要求，需要较高的采样率来获得满意的图像质量[7]。相比而言，迭代重建算法对数据的完备性要求不高，可以通过引入图像先验约束信息，提高重建质量[8]。

2006年，Sidky等引入全变分(TV)最小化的概念，提出了一种TVM-POCS(Total Variation Minimization-Projection Onto Convex Sets)算法，用于从稀疏采样或稀疏角度投影数据进行CT图像重建[9]。但由于图像的分段常数假设，在图像重建过程中，会产生阶梯伪影以及图像边缘过度平滑的结果。因此，许多TV算法的变体被提出且被用于CT图像重建。Kim H等提出了一种新的非局部全变分算子(NLTV)[10]；Jin等提出了一种基于各向异性全变分(ATV)的有限角CT图像重建方法[11]；Wang等提出了一种新的迭代加权各向异性全变分方法(RWATV)[12]；Guo等提出了一个加权方向全变分(WDTV)最小化模型[13]；Qu等提出了一种新的基于梯度方向全变分(BDTV)最小化算法，自适应选择变化梯度方向计算方向差算子[14];Xi等提出了一种高阶全变分(HOTV)重构模型以提高其重建去噪效果，且在一定程度上保护图像的边缘信息[15];Kim等提出了一类新的非局部全变分，结合一阶和二阶导数，以很好地保持图像的平滑度，平衡一阶导数引起的阶梯伪影现象[16]；Sagheer等提出了一种通过低秩张量建模和全变分正则化的方法对低剂量CT图像进行去噪[17]；Li等提出了一种结合使用广义全变分(PWLS-TGV)和字典学习(DL)的惩罚加权最小二乘法来恢复图像[18]；Kai等将一种基于图像贴片匹配的非局部三维剪切稀疏正则化用于稀疏角度CT图像重建，有效抑制噪声，提高重建图像质量[19]；时鸿雁等提出了一种基于导引图像滤波(GIF)和截断全变分的CT重建算法[20]。这些方法与传统的TV模型相比，在一定程度上，有效抑制了噪声，但在边缘保护、图像局部细节保护方面仍有所欠缺。

l0范数的高稀疏性，使得l0范数梯度正则化在图像去噪和保护边缘特征方面有着明显优势。Xu等提出了一个有限角度X射线CT的重建模型，交替保边延拓和保边光滑算法(Alternating Edge-preserving Diffusion and Smoothing, AEDS)，包含两个正则化项，在两个方向起到保边扩散和平滑的作用，并提出了一种交替最小化算法对模型进行近似求解，该方法在有限角度的重建过程中能较好地去除伪影，保留图像边缘，得到更好的重建图像[21]。

针对在稀疏角度CT重建中仅仅使用一个约束，不能很好地兼顾去噪和保边的问题，本文基于迭代重建算法，将AEDS应用于稀疏角度的重建算法，对模型添加两个正则项约束，提出了一种基于TV和AEDS的双约束稀疏角度CT重建算法。该重建算法首先使用ART迭代重建算法，得到初步的迭代重建图像，然后使用TV继续重建图像，最后使用AEDS，分别在x和y方向引入一个正则化项，进行一定的稀疏变换，达到边缘保护的作用。

1 CT重建算法

1.1 CT重建模型

在理想的CT成像系统中，图像重建满足以下方程：

Au=p

(1)

式中，u为待重建图像矢量；p为探测器在不同角度的投影数据；投影矩阵A关联了图像矢量u和投影矢量p，A=[aij]∈RI×J，其中I为射线总数，J为图像的像素总数，aij为j个像素对第i个投影数据的贡献。CT重建过程是从投影数据p中重建图像u的过程，其实质就是线性方程组的求解过程。

由于投影数据的不完备性，稀疏角度CT重建是一个不适定问题。对于此类问题，通常引入正则化项，增加先验条件约束，优化模型为：

(2)

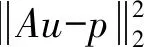
1.2 基于TV和AEDS的CT重建算法

基于全变分的CT图像重建算法。其重建算法的目标函数为：

(3)

(4)

式中，x和y为像素位置；ux,y为图像在(x,y)处的像素值。该优化问题使用梯度下降法进行求解。

AEDS在有限角度的重建中取得了较好的重建效果，该算法是在x和y方向分别引入一个正则项，使图像趋近于分片常数的作用，其优化模型为：

(5)

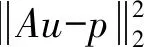
(6)

式中，sgn为符号函数，其属性为sgn(0)=0。

AEDS经验证，可以有效地保护重建图像的边缘，充分利用图像的稀疏性，弥补以TV作为正则项在重建图像过程中造成边缘结构过度平滑，细节丢失的问题。因此，本文将TV与ADES相结合，提出一种新的CT重建算法，构建目标函数为：

(7)

式中，μ为惩罚参数；λ1，λ2和λ3分别用来调节正则化项在优化目标函数中的作用。

1.3 优化算法

最优化问题(5)可能是非凸的，我们采用一种交替极小化方法进行求解(7)。主要内容如下：λ为正常数，令u(t)表示第t次迭代的结果，第t+1次的迭代结果可依次求解以下四个子问题得到：

子问题1：

(8)

子问题2：

(9)

子问题3：

(10)

子问题4：

(11)

子问题1的求解，使用ART进行一次迭代，有：

(12)

子问题2使用梯度下降法进行求解，首先确定梯度下降方向

(13)

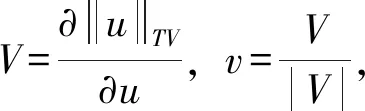
(14)

子问题3可以分解为一系列一维问题，首先引入一个辅助变量

g={gij|i=1,2,…,K1,j=1,2,…,K2}

(15)

令gn=gij，其中n=(i-1)K2+j。则子问题3可以转化为

(16)

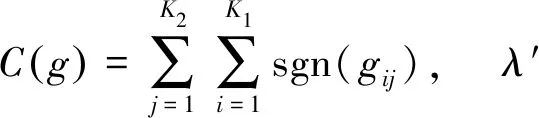
1)更新重建图像u，u的求解相当于最小化问题

(17)

由于是二次函数，故有一个全局最小值，得

(18)

2)更新g，其目标函数为

(19)

得g满足以下条件：

(20)

子问题4的求解同理子问题3。

2 实验仿真

2.1 实验设置

本文以Shepp-Logan Phantom和胸部图像作为仿真模型，以验证所提出TV-AEDS算法在稀疏角度CT重建中的性能(图1)。为了更好地模拟真实的CT场景，在投影正弦图中加入泊松噪声，泊松噪声的量子数为106，以验证算法对噪声的鲁棒性。该实验中X射线源到物体的旋转中心的距离为1000，射线源到探测器的距离为1300，探测器的个数为392，重建图像大小为256×256。在稀疏投影角度的重建中，影响重建质量的主要因素是投影角度的个数。因此，在本实验中，在360°范围内等间隔采样，采样间隔分别为12°、6°、4°，得到稀疏投影角度数目为30、60、90。

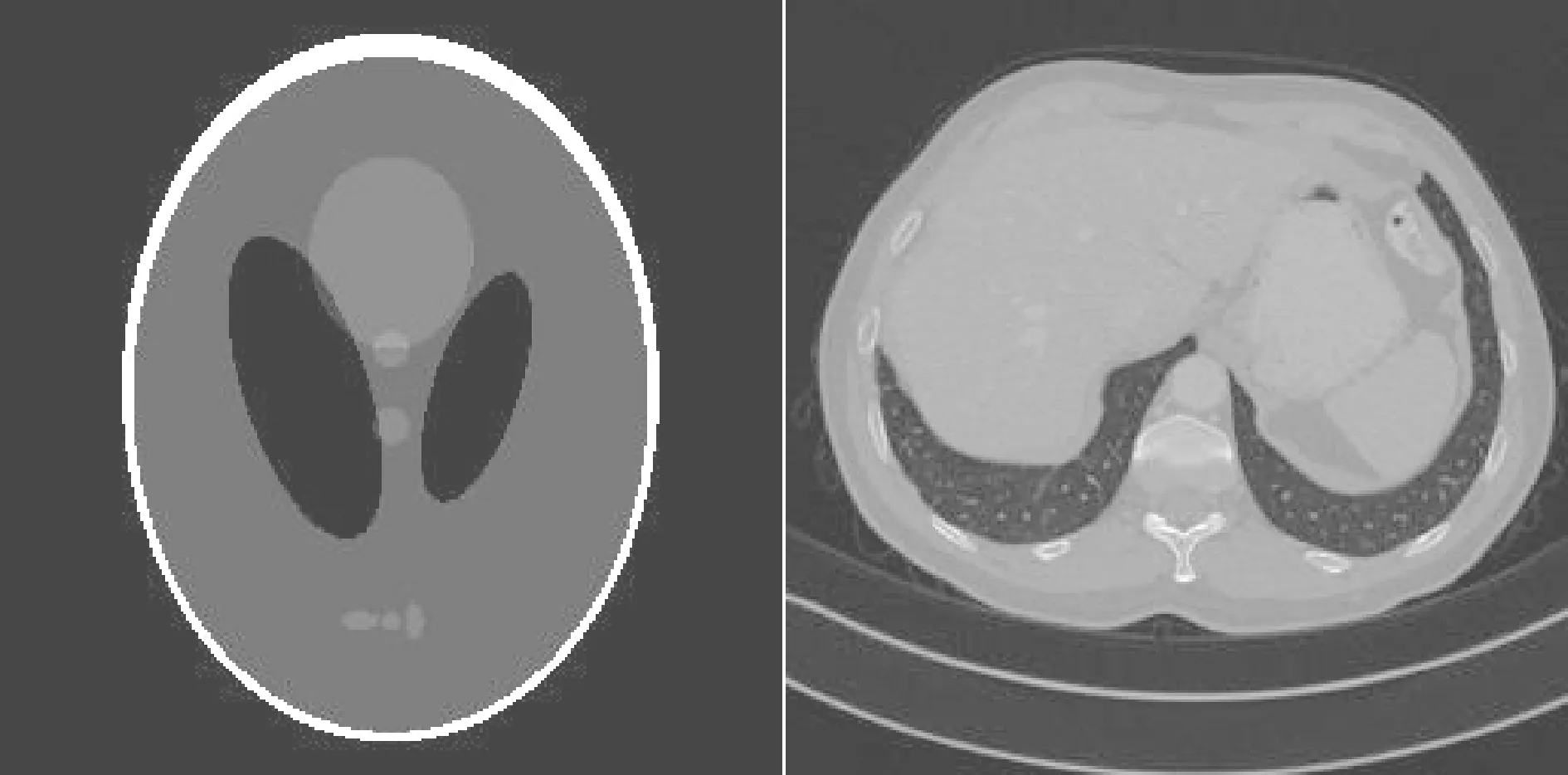
图1 两种模型，分别为Shepp-Logan Phantom和胸部图像

在本文的实验中，迭代算法的参数以及迭代次数均通过经验选取，为公平起见，所有参数都一致。迭代次数均设置为1000次，迭代算法中的λ设置为1。为了进一步定量客观评价算法的性能，本文使用峰值信噪比(PSNR)[23]、均方根误差(RMSE)[24]和通用质量指标(SSIM)[25]来定量地评价重建质量。PSNR用来衡量重建图像质量的高低，值越高，重建图像质量越高；反之，重建图像质量越低。RMSE用来衡量重建图像与参考图像的像素相似性，值越小，相似性越高；反之，相似性越低。SSIM值越接近1，则重建图像越接近真实图像。本文所有算法在Visual Studio 2013和Matlab 2019a上运行[配置Intel(R) Core(TM) i5-10210U CPU @ 1.60GHz 2.11GHz]。

2.2 Shepp-Logan Phantom重建结果分析

ART-TV算法、ART-AEDS算法、ART-BDTV算法[20]和TV-AEDS算法重建的Shepp-Logan Phantom重建结果如图2～图4所示。由图可知，稀疏投影角度数目为30个时，重建图像最差，图中存在大量噪声，且图像模糊。随着稀疏投影角度数目的增加，重建效果越来越好。以稀疏投影角度为60个的重建结果为例，ART-TV算法和ART-AEDS算法的重建结果均存在条纹伪影，ART-BDTV算法中有所缓解，效果明显，而本文提出的算法几乎完全消除了噪声，且图像结构清晰。

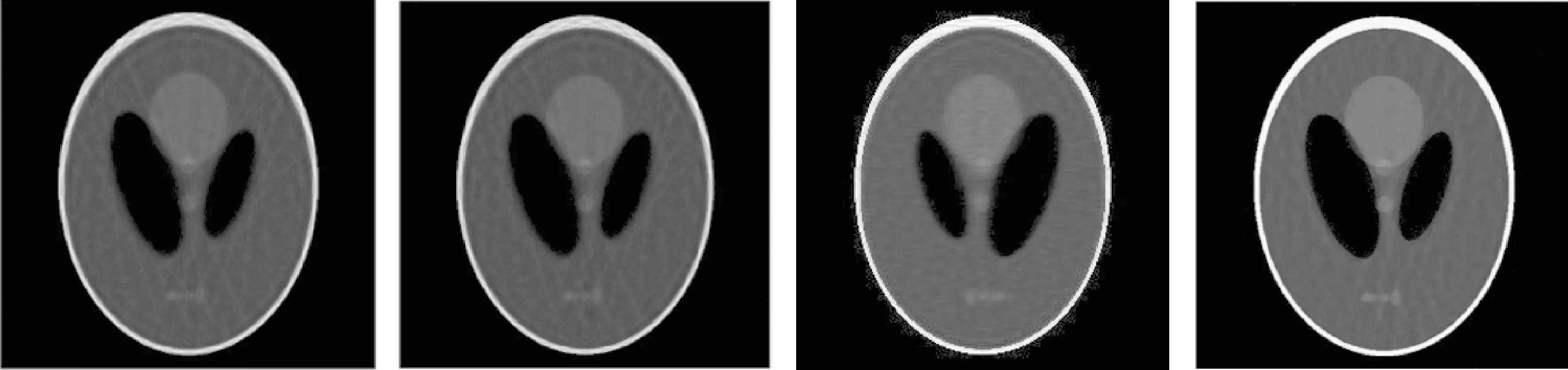
图2 稀疏投影角度数目为30，分别为ART-TV、ART-AEDS、ART-BDTV和TV-AEDS算法的重建结果

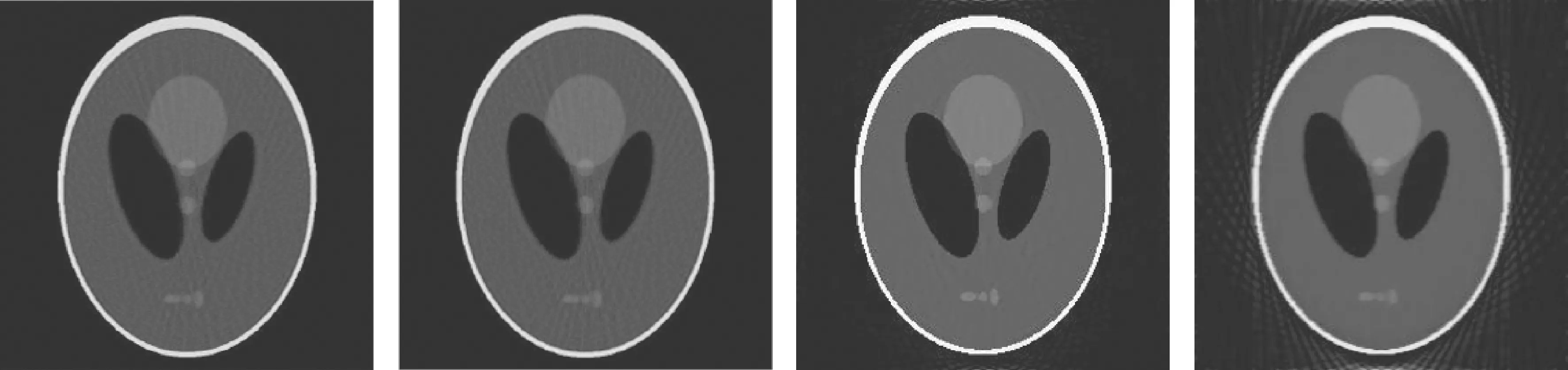
图3 稀疏投影角度数目为60，分别为ART-TV、ART-AEDS、ART-BDTV和TV-AEDS算法的重建结果

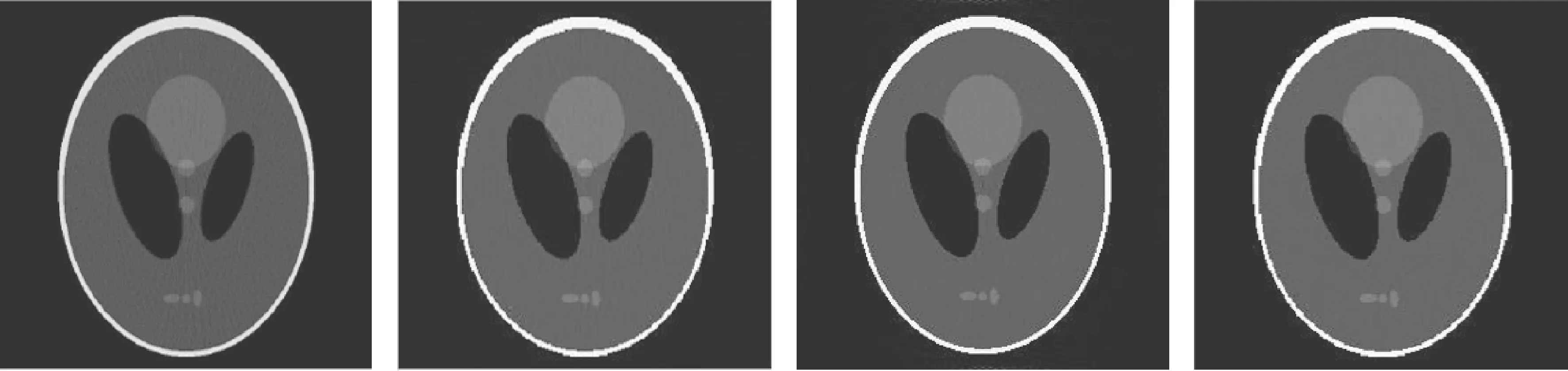
图4 稀疏投影角度数目为90，分别为ART-TV、ART-AEDS、ART-BDTV和TV-AEDS算法的重建结果

四种算法下PSNR、RMSE以及SSIM的定量评价结果如表1所示。由表可知，本文所提算法的PSNR值最高，RMSE值最低，SSIM值最接近1。因此，本文算法的重建效果相比于其他算法更好。

表1 不同算法在不同稀疏角度下的量化结果

2.3 胸部图重建结果分析

ART算法、ART-TV算法、ART-AEDS算法和TV-AEDS算法重建的胸部图重建结果如图5～图7所示。几种算法相比较而言，以60个投影角度为例，ART算法的重建结果存在大量的噪声，且图像较为模糊，结构几乎分辨不出来。ART-TV算法和ART-AEDS算法的重建结果噪声虽然有所减少，但图像结构仍然很模糊。TV-AEDS算法可以抑制更多的噪声且重建结果很清晰，边缘细节保护良好，结构完整，可以很好地辨别血管、阴影等情况。

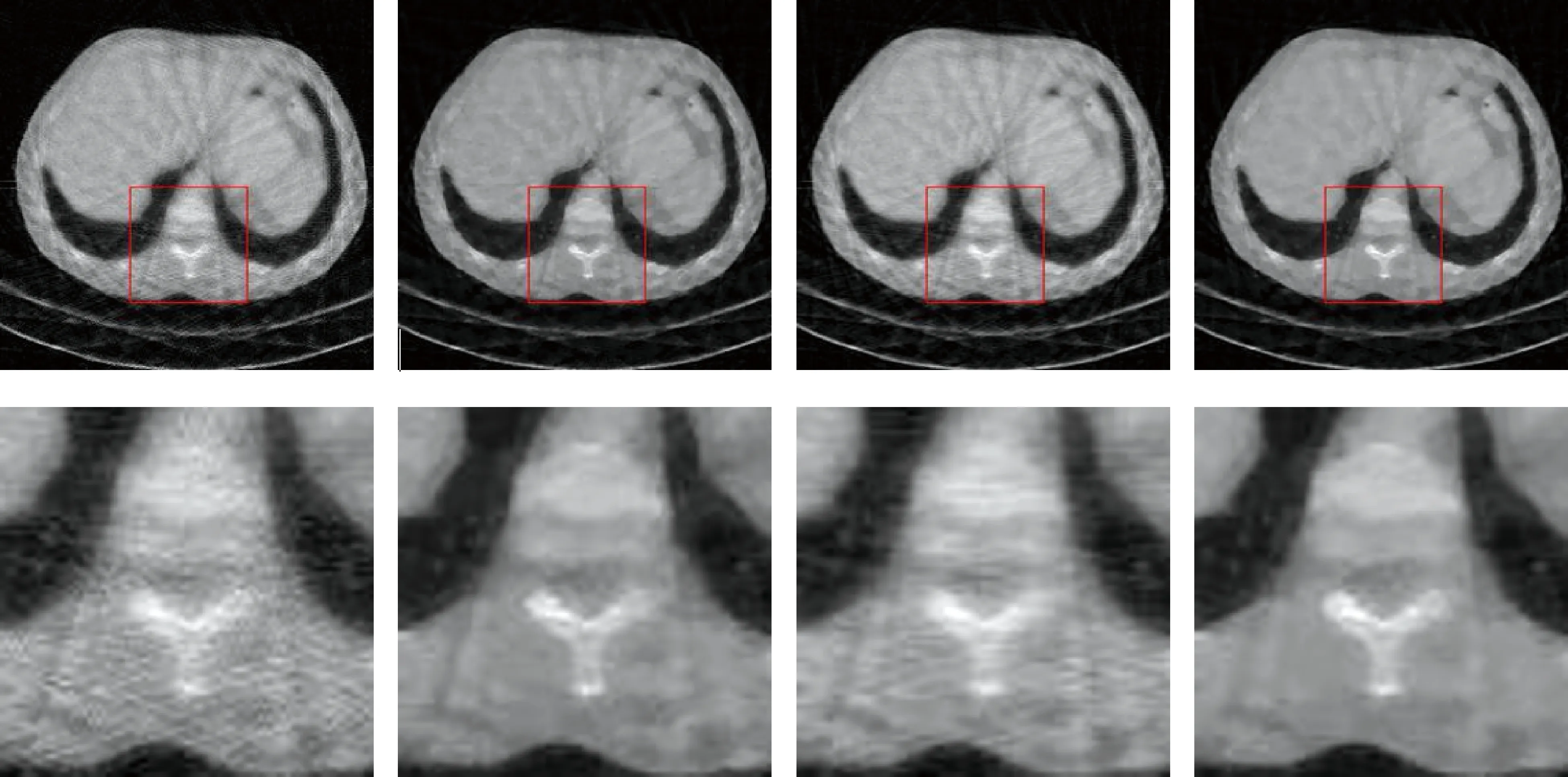
图5 稀疏投影角度数目为30，第一行分别为ART、ART-TV、ART-AEDS和TV-AEDS算法的重建结果；第二行分别为相对应的重建图像方框区域的放大图

图7 稀疏投影角度数目为90，第一行分别为ART、ART-TV、ART-AEDS和TV-AEDS算法的重建结果；第二行分别为相对应的重建图像方框区域的放大图

四种算法下PSNR、RMSE以及SSIM的定量评价结果如表2所示。由表可知，本文所提算法的PSNR值最高，RMSE值最低，SSIM值最接近1。因此，本文算法的重建效果相比于其他算法更好。

图6 稀疏投影角度数目为60，第一行分别为ART、ART-TV、ART-AEDS和TV-AEDS算法的重建结果；第二行分别为相对应的重建图像方框区域的放大图

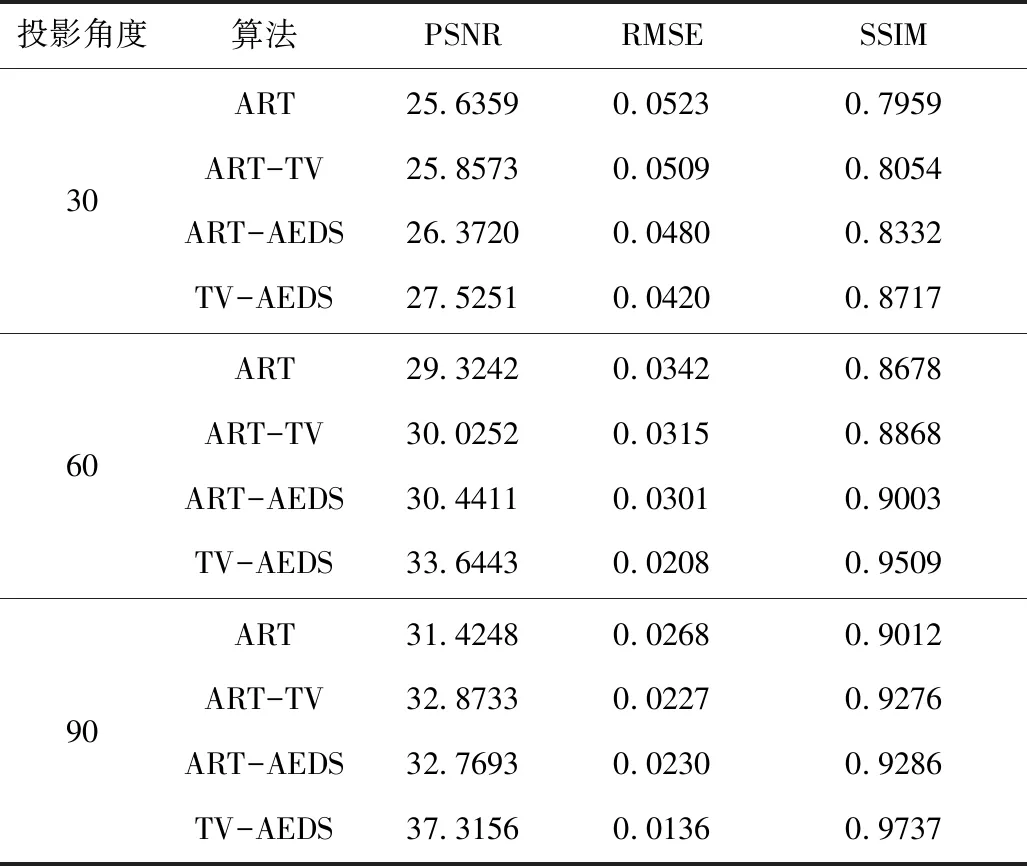
表2 不同算法在不同稀疏角度下的量化结果(胸部图像)

3 结论

为了提高稀疏角度CT图像重建质量，本文提出了一种基于TV和AEDS算法的稀疏角度迭代重建算法。通过引入AEDS算法，在水平和垂直两个方向利用l0范数的高稀疏性，保留了图像的更多边缘结构和细节，使重建图像的边缘以及微小细节得到了更好的重建效果。实验结果表明，与其他算法相比，本文提出的稀疏角度重建算法有较好的性能，不仅可以有效地抑制噪声，而且能够很好地保护图像边缘信息和细节特征。