场区飞机滑行效率评价模型的设计与仿真

耿 宏，朱 浩

(中国民航大学电子信息与自动化学院，天津 300300)

1 引言

随着经济的高速发展，航班量日益增长，我国大型民用机场的航班延误情况也开始越来越多。虽然导致航班延误的因素是多种多样的，但是场区飞机滑行效率较低是影响航班延误的主要原因[1]。分析影响场区飞机滑行效率的各种因素，准确评价滑行效率，对减少航班延误，改善飞机滑行阶段的薄弱环节具有重要的价值和意义。

由于飞机在滑行过程中各种不确定性[2]，导致航班延误问题日益严重，相关专家也开始将研究核心转移到优化飞机滑行路径方面，确保场区飞机滑行效率得到有效提升。国内外相关专家重点针对场区飞机滑行效率评价方面的内容进行了大量研究，并且给出了一些较好的研究成果。例如姜雨等人[3]将航天器在滑行系统中的最短滑行距离作为目标函数，同时构建滑行时空协同优化模型，最终完成滑行效率评价。谷润平等人[4]分析飞机的导航能力，构建飞行侧向偏差模型和飞行高度偏差模型，计算实际飞行轨迹和定义航径之间的偏差，进而对偏差进行统计，根据统计结果进行评价。由于上述两种评价模型未能在具体评价的过程中加入ISM-AHP-HFS联合方法，导致评价结果的误差和费用的大幅度增加。为了更好地解决上述问题，提出一种基于ISM-AHP-HFS的场区飞机滑行效率评价模型。测试结果表明，所提模型能够有效降低评价费用，获取理想的评价结果。

2 场区飞机滑行效率评价模型

2.1 滑行效率影响因素识别和筛选

为了更好地构建场区飞机滑行效率评价模型，需要优先了解飞机进场和离场的滑行过程。对于单个航班，即一架飞机来说，滑行效率即飞机的滑行时间，从飞机停机位推出到离开跑道起飞的时间总和。当确定滑行路径后，滑行时间=滑行距离/滑行速度。对于连续时间内的航班而言，滑行效率主要是指设定时间内所有航班的平均滑行时间。另外，滑行时间还包括飞机在停机位的等待和在跑道头等待的总时间。部分欧美国家采用畅通滑行时间来衡量滑行效率[5，6]，对于整个机场来说，滑行效率指的是航班整个过程的参与者，包括空管、航空公司、机场、旅客对滑行时间所做的“贡献”，包括空管放行，地面服务保障，旅客安检，滑行路径规划等。

在滑行的过程中，可能会出现以下几方面的冲突：交叉冲突；对头冲突和追尾冲突。为了更加全面掌握影响场区飞机滑行效率的因素，需要尽可能获取影响飞机滑行的全部关键点。由于涉及的内容比较广泛，将全部影响滑行效率的因素进行合并，获取的客观指标和主观指标如表1和表2所示。

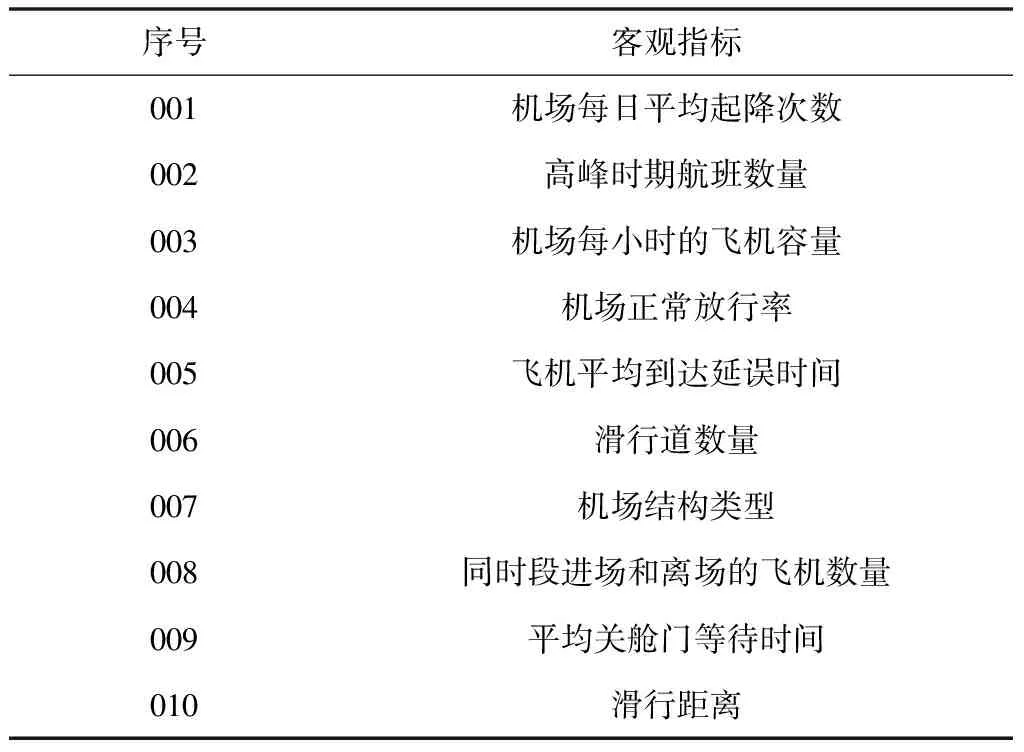
表1 滑行效率客观指标

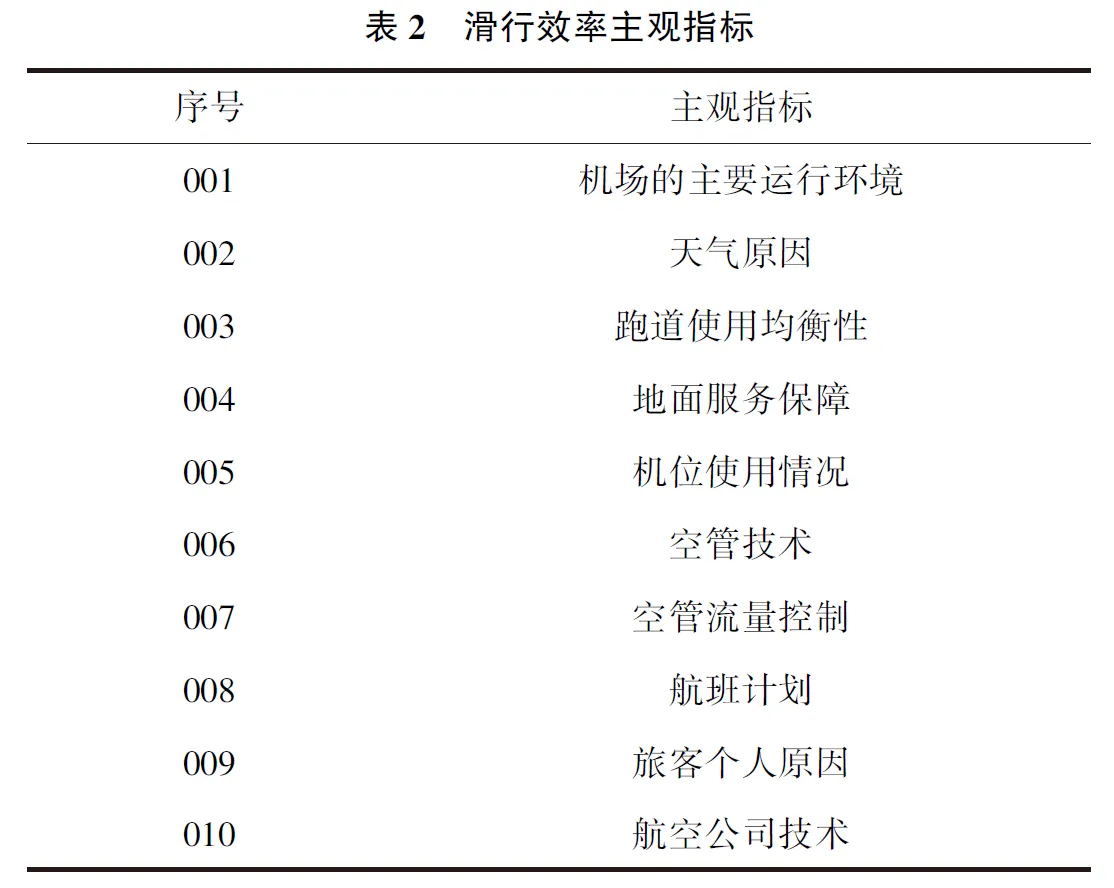
通过影响指标的相关定义，将上述指标分别划分为客观指标和主观指标，通过ISM分析各个指标之间的关联性[7，8]。ISM模型的主要目的就是将复杂的问题简单化，尽量选取核心体系。设定aij代表布尔矩阵中的元素，则各个元素之间的关联性能够表示为

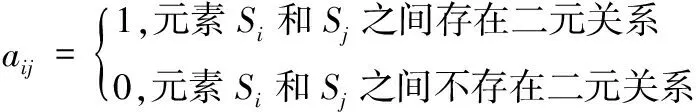
(1)

其中，可达矩阵是通过矩阵的形式表示在较长一段时间内一定长度路径后达到有向图中各个节点的程度。优先利用可达矩阵M计算可达集合P(Si)和先行集合Q(Sj)，则有

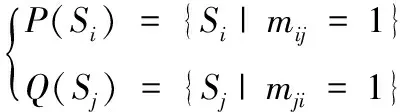
(2)

其中，可达集合中元素Si就是可达矩阵M上第i行对应的影响因素取值；先行集合中元素Sj就是矩阵M中第j行对应的影响因素取值。将上述两种集合相结合，获取共同集合L(Sij)：

L(Sij)={Si|P(Si)}∩Q(Sj)=P(Sij)

(3)

接下来，使用优先的层级抽取规则方法进行层级划分，同时根据层级划分结果将元素放置到对应的层次中，同时将可达矩阵转换为多个不同的矩阵，利用有向分支将各阶要素进行连接，构建低阶层次结构图[9]，进而得到各个影响因素之间的主要关联。

通过主成分分析法对各项指标进行识别和筛选，最终的指标筛选结果如表3所示。

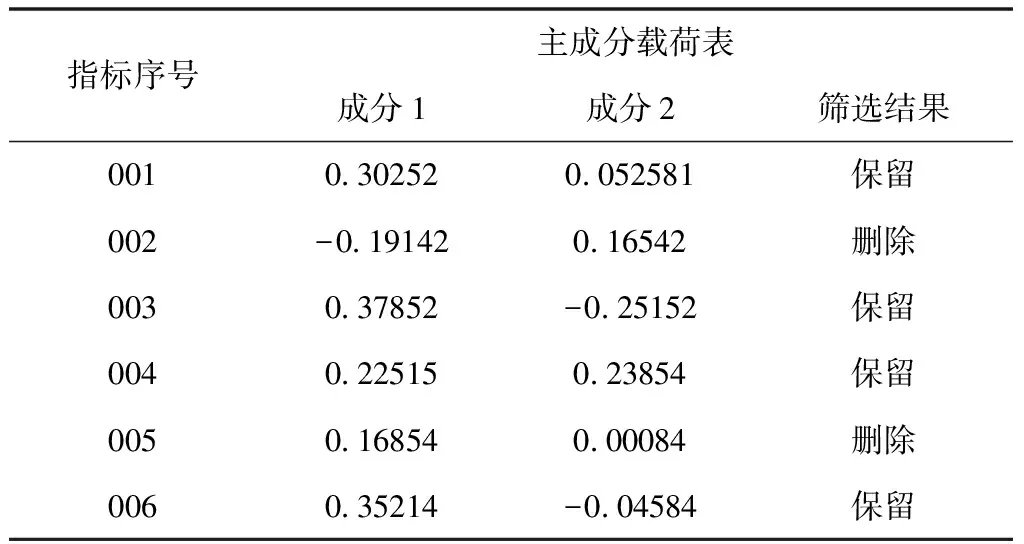
表3 评价指标筛选结果

为了确保指标的科学性，需要筛选出主要的场区飞机滑行效率指标，对民航领域相关的专业人员进行问卷调查。分析最终的统计结果，删除得到最低的四项，获取有效的指标，对指标进行分类，得到如图1所示的指标体系。

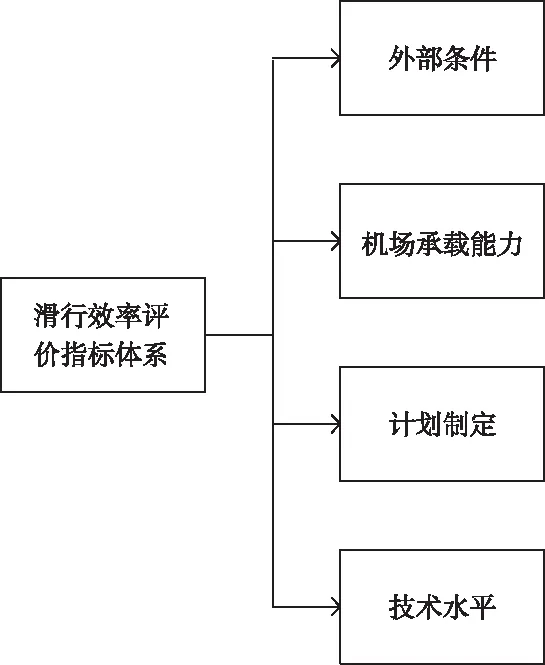
图1 滑行效率评价指标体系

2.2 基于ISM-AHP-HFS的场区飞机滑行效率评价模型的建立

结合2.1小节对场区飞机滑行效率影响因素之间的关联性分析，将分析结果设定为层次结构模型的输入，主要通过ISM-AHP-HFS三者相结合的方式构建厂区滑行效率评价模型，具体的操作步骤如下所示：

通过对研究对象深入地调查和分析，获取评价对象的关键要素[10]，同时将各个重要的影响因素通过层析结构进行分解，其中层次结构模型如图2所示。

图2 层次结构模型

对各个研究对象周边的环境和自然因素进行深入分析，进而从代表性以及系统性等多个角度出发，组建场区飞机滑行效率评价指标体系。为了更好观察各个指标的变化规律，优先对全部评价指标进行标准化处理，如式(4)所示

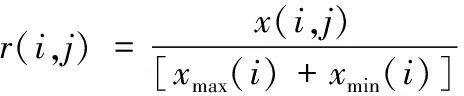
(4)

其中，r(i，j)代表经过标准化后的评价指标取值；x(i，j)代表未进行评价的样本数据；xmax(i)代表样本集中第i个评价指标的最大值；xmin(i)代表样本集中第i个评价指标的最小值。

通过式(5)对越小越优型指标进行标准化处理

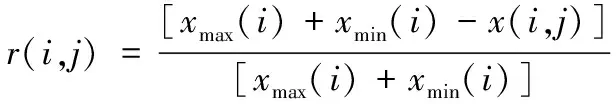
(5)

通过式(6)对越中越优型指标进行标准化处理

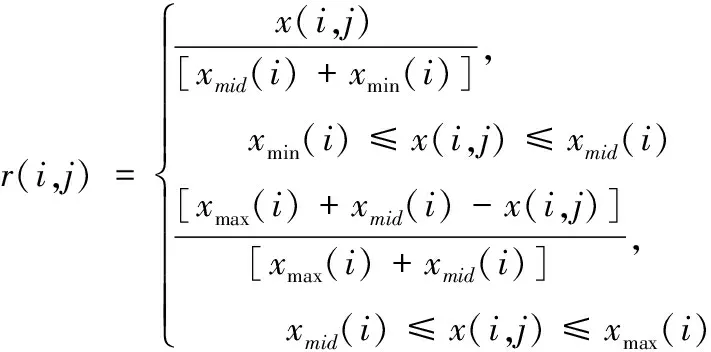
(6)

根据模糊评价矩阵R组建判断矩阵B，主要目的是筛选具有价值的评价指标。通过模糊综合评价方法进行评价的过程即选取最优评价指标的过程。接下来从综合评价角度出发[11]，设定评价指标1比评价指标2中的样本变化趋势更加明显，证明评价指标1中传递的信息更多且更有价值。结合上述分析，对各个评价指标的样本差进行计算，具体如式(7)所示

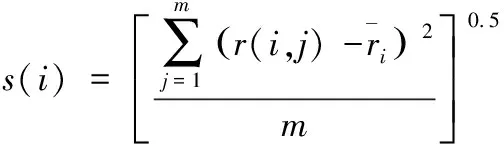
(7)

通过式(7)全面描述评价指标对综合评价的影响程度，同时应用其构建判断矩阵B

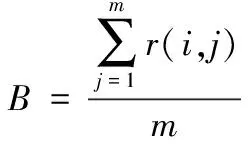
(8)

式(8)代表各个评价指标下样本系列的平均取值。通过式(9)获取1～9级的判断矩阵，即

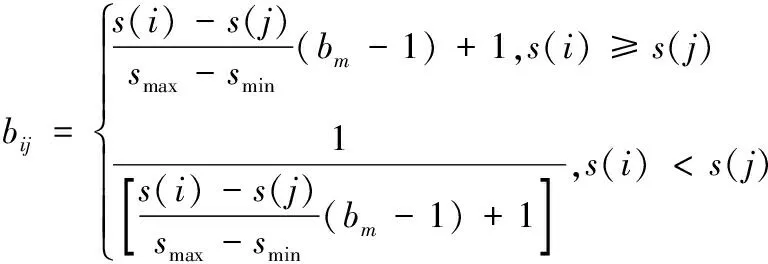
(9)

其中，smin和smax分别代表s(i)的最小值和最大值；bm代表相对重要性程度参数。

对判断矩阵进行一致性检验以及修正等相关计算，要求判断矩阵B必须满足以下的约束条件

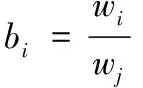
(10)

当判断矩阵的维数偏高时，通过相关定义计算判断矩阵的特征值和特征向量。利用算法平均方法计算各个指标的加权平均列向量，如式(11)所示

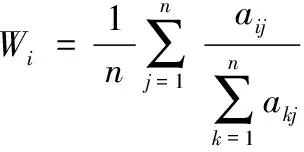
(11)

一致性比率计算需要优先计算判断矩阵的最大特征根，以下选取方根方法计算最大特征根。

优先计算判断矩阵M中各行的乘积几何平均值di

(12)

将全部向量进行归一化处理，获取如式(13)所示的特征向量

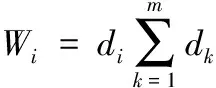
(13)

通过特征向量计算得到最大特征根，即

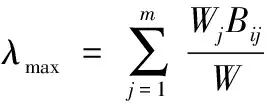
(14)

对判断矩阵进行一致性检验，假设通过一致性检验，则将全部向量进行归一化处理，得到对应的权重向量；反之，则重新组建判断矩阵。

在上述分析的基础上，结合滑行效率评价指标体系，邀请具有经验的专家对各个大型机场中评价指标对滑行效率的影响进行评价打分，将重复数据删除，同时利用专家的可信度，构建具有可信度的犹豫模糊评价矩阵[12]。

通过具有可信度诱导犹豫模糊加权算子对犹豫模糊作为数据进行集成，获取信息集成值构建信息集成矩阵，具体结果如表4所示。

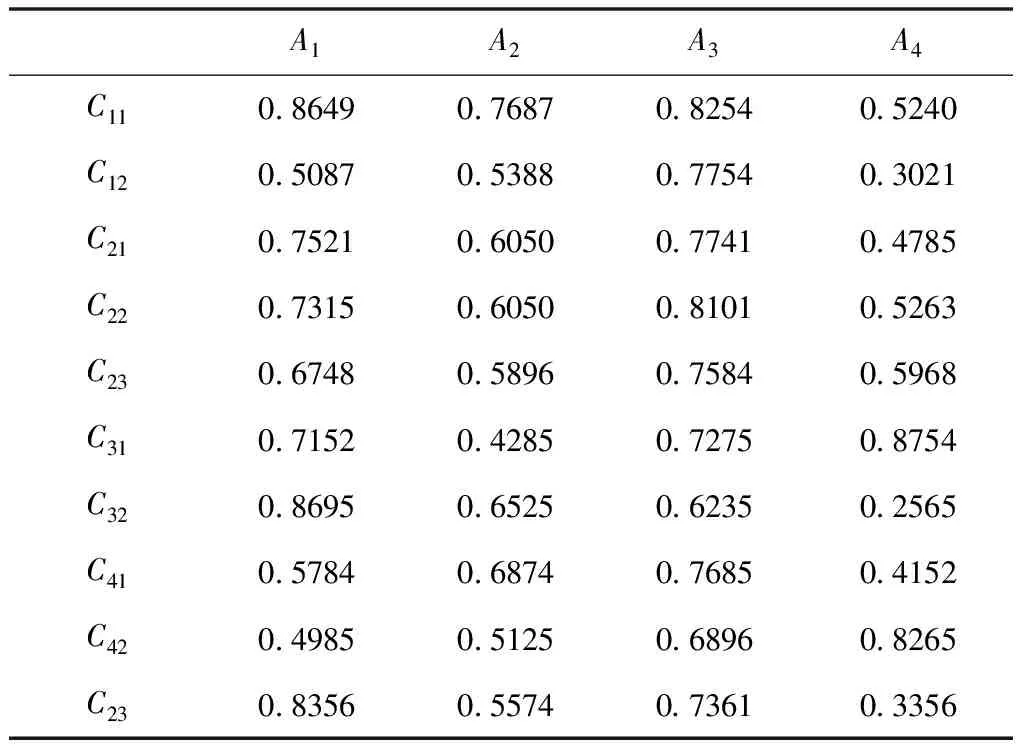
表4 信息集成矩阵

通过犹豫模糊距离公式，分别计算各个指标中的犹豫模糊基本元素和对应属性集成值之间的测度，获取距离矩阵

D=(dij)10×4

(15)

根据标准，直接设定一致性阈值，将犹豫模糊源内距离测度作为研究基础，进行一致性检验。

对全部指标进行综合一致性评分，根据评分结果组建场区飞机滑行效率评价模型，通过模型实现最终的评价。

3 仿真研究

为了验证所提基于ISM-AHP-HFS的场区飞机滑行效率评价模型的有效性，选取场面航空器滑行效率评价模型和民用飞机RNP导航能力的适航评估模型作为对比对象进行测试。

为了验证评价模型获取的评价结果是否可信，将均方根误差、平均绝对误差以及相对误差设定为衡量指标，具体的实验对比结果如表5～表7所示。

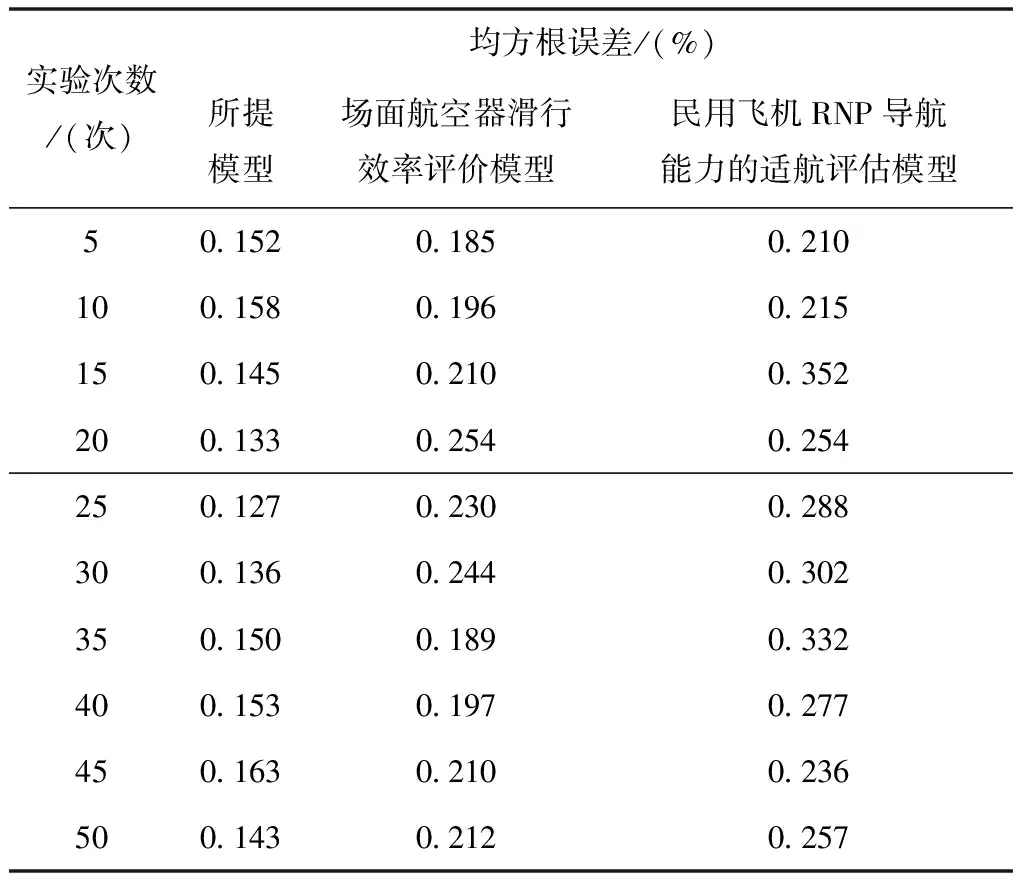
表5 不同模型的均方根误差对比结果

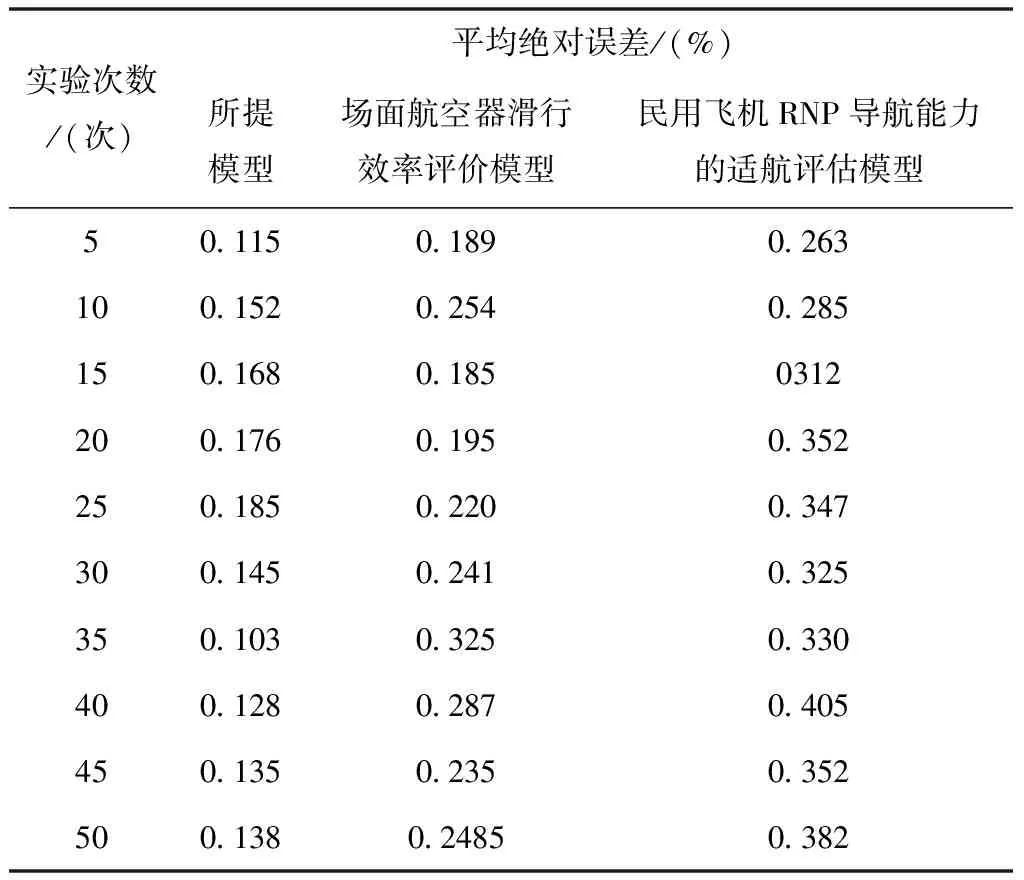
表6 不同模型的平均绝对误差对比结果

表7 不同模型的相对误差对比结果

分析表5至表7中的实验数据可知，随着实验次数的增加，各个方法的各种评价指标也发生了十分明显的变化。由于场面航空器滑行效率评价模型和民用飞机RNP导航能力的适航评估模型未能在评价的过程中加入ISM-AHP-HFS联合方法，促使两种模型的均方根误差、平均绝对误差以及相对误差明显更高一些，充分验证了所提模型的优越性，同时也说明所提模型能够获取更加精准的评价结果，且评价结果更加可信。

为了更全面地验证所提模型的优越性，以下实验测试对比三种模型的评价费用，具体实验对比结果如图3所示：

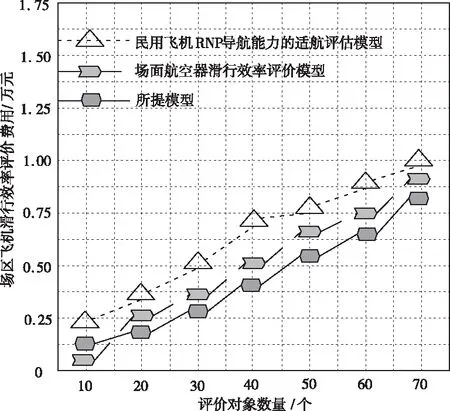
图3 场区飞机滑行效率评价对比结果

分析图3中的实验数据可知，所提模型的场区飞机滑行效率评价费用在三种评价模型中为最低；场面航空器滑行效率评价模型的评价费用次之；民用飞机RNP导航能力的适航评估模型的评价费用最高。由此可见，所提模型加入ISM-AHP-HFS三种联合方法进行评价是有效且可行的。

4 结束语

现阶段我国对于场区飞机滑行效率方面的研究内容仍然处于起步阶段，开展相关对于提升场区飞机滑行效率具有十分重要的意义。提出一种基于ISM-AHP-HFS的场区飞机滑行效率评价模型，仿真结果表明，所提模型能够获取准确的评价结果，同时还能够有效降低评价费用。

所提模型由于受到研究时间和环境的限制，仍然存在一定的不足，后续将重点针对以下几方面的内容进行研究：

1)进一步研究外界因素对评价结果产生的影响。

2)综合分析各个机场的实际情况，进而对滑行路径进行规划。